基于组合优化算法的智慧高校建设评估方法的研究与设计*

陶 槊，魏东东，徐光明

(合肥科技职业学院 经济管理系， 安徽 合肥 231201)

近年来，随着我国智慧化校园建设的全面推进，教育主管部门和各院校信息部门都在积极开展“高校智慧化建设评价指标体系”工作。与此同时，大数据技术的成熟，智慧化校园建设亟待研发一套智能评估工具，借助高效算法，充分利用好海量的评价数据，促进高校提升智能信息系统建设，并为智慧化校园建设构建一套行之有效的综合评估指标体系。

目前国内外对高校信息化水平科学评估方法已有许多研究成果与案例，如美英学校技术与就绪(school technology and readiness，STaR)量表评估体系和学校信息化自我评估框架(the self-review framework, SRF)[1]，日本2018年通过的《平成30年的学校信息与通信技术(information and communications technology, ICT)环境建设方针》，对院校信息化建设评估进行规范[2]。在我国，基本研究基于国家-省2级研究课题展开，主要集中在教育手段、基础建设、应用水平、决策分析、模型架构等5个方面[3-4]，初步构建了一套我国的高校教育信息化的理论评估体系。

但通过调研发现，高校评估方法更多的关注于单方面指标体系的分析与评估，特别是缺少对智慧校园指标体系的综合化应用与研究。同时在算法构建上，主要是模糊数学[5]、层次分析、指标聚合[6]、神经网络等方法[7]，这样容易受主观判断或等级评价的模糊性影响，难以反映信息化建设具体变化情况，或者是计算复杂，实现困难。另外，因校际间建设水平、发展方向与理念的不同，势必造成具体建设指标差异大，难以帮助高校起到引领示范作用。因此根据以上情况，本文主要进行了以下工作：(1)以权威性的指标体系为基础，对客观软硬件指标内容细化与量化，以院校门户网站生成的后台评分大数据为基础进行收集，清洗、整理生成主观评价数据；(2)引入层次化分析与主客观评估模型。然后通过组合优化算法，确定权重，整合各项评分，获得综合评估结果；(3)通过试验验证评价算法的可靠与适用性，利用该组合评估算法模型发现智慧高校建设发展特点。

1 评估模型

由上级部门颁发的各类评估指标文件对高校信息化建设起到了指导示范作用，但各个指标系之间都或多或少存在约束关系，为能全面反映智慧化建设成果，需实施3方面的工作：(1)建立基本框架模型(见图1)，组织指标体系与关系，明晰架构与规范流程；(2)在各约束条件与对应评估指标之间寻找1种优化组合方法，平衡各评分系统权重关系获得最优解，体现了主客观评价的统一；(3)利用新技术，以高效算法生成更加科学化评估体系，又能反过来指导智慧高校建设。

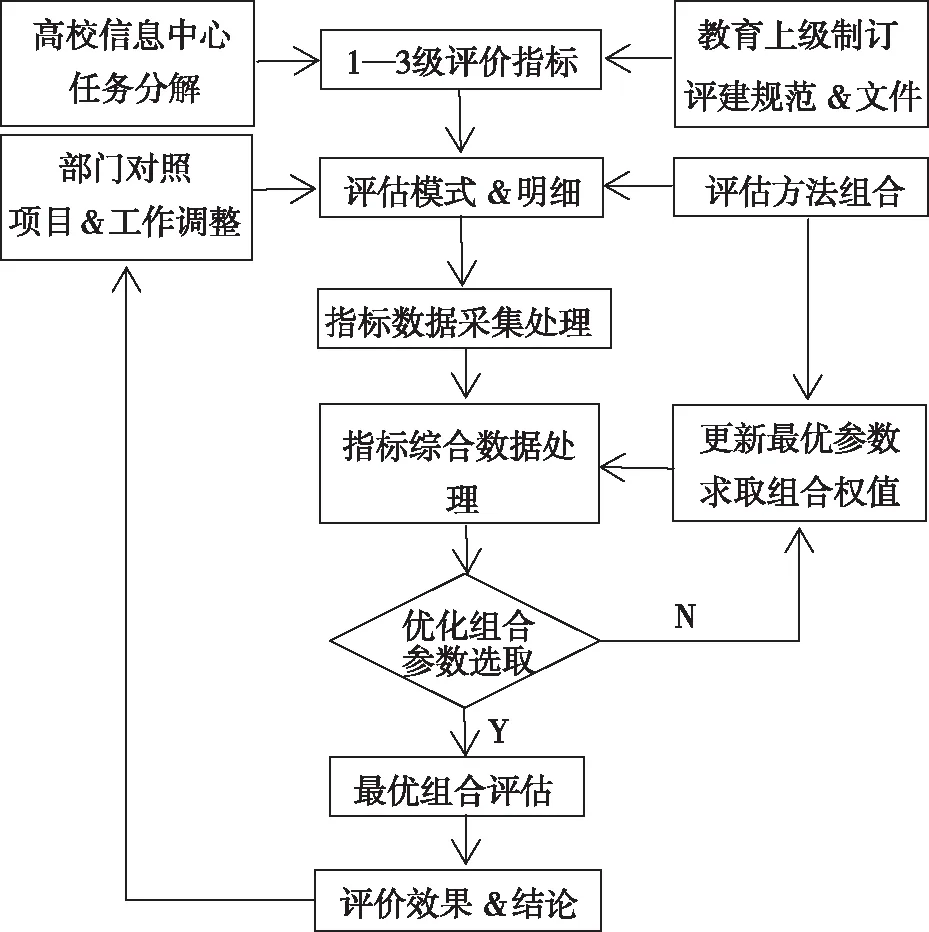
图1 高校信息化评估模型

1.1 评估指标

本文以2021年3月教育部颁布的《高等学校数字校园建设规范(试行)》(教科信函[2021]14号)和安徽省教育厅《高等学校教育信息化建设评价指标体系2.0》(皖教秘科[2021]11号)指导文件为基础，对已有的指标体系的评分体系进行系统研究，确定3级评价指标内容，作为客观性智慧校园建设评价指标依据，编制6维度3级指标体系(见表1，限于篇幅，第3级指标略)。

1.2 大数据的收集与处理

以表1为蓝本，制作调查项目，在高校已建立的门户网站、贴吧、论坛上做问卷调查、满意度调查、抽奖投票、意见反馈获得业务支撑与业务应用的主观评分。利用教研、图书馆、OA、云课堂、慕课(massive open online course，MOOC)、仿真实验等平台，通过项目申报、考试测评、学术调研、在线评价形式收集与整理综合数据，并对数据进行指标化统一与量化。对无法在线计分的项目，如基础设施，数据资源量，安全保障，运维管理体系等，则直接按照《指标体系2.0》要求，一部分划分层次等级，一部分按数量做分值统计，然后实现对所有项目的指标的标准化处理。

表1 校园智慧化信息系统评估指标表

2 基本评估算法

层次化、模糊评估与遗传、神经网络算法评估各有优劣，层次化法减少了主观判断的随意性，但全面性反映能力不足，模糊评估法更能反映智慧化校园建设的实际效果，但对数据限制和操作人员要求高，实效性不足[4,7-8]，本文采用层次评估与系数统计组合算法作为智慧高校评估手段，以方便体现高校信息化建设综合能力，弱化算法的不足。

2.1 层次评估法

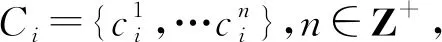
(1)

于是得单级权值评估公式：

(2)

利用三角模糊算法简化一致性判断矩阵：

(3)

转换并求模糊一致性矩阵Q：

(4)

归一化处理后，指标i的权值wi：

(5)

2.2 变异系数法

智慧化建设涵盖内容多样，各个项目不能简单进行分值累加，否则很容易造成各校评价分值片面化，忽略自身实际建设需求。所以本文采用变异系数法[10]，同时可以消除不同指标间的不同量纲效应，并通过权值变化来反映异化数据间的差距与不同。

根据高校建设项目，校际间评比，适于采用高优指标，此数据越高越好：

(6)

如果是为寻找本校建设短板，则采取低优指标：

(7)

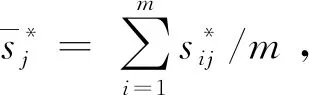
(8)

得权值：

(9)

3 优化处理

3.1 权重优化模型

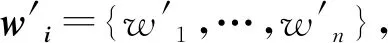
Lc(x,λ,μ)=f(x)+μh(x)+c|h(x)|2/2

(10)

对等式约束的非线性优化：

(11)

f(x):Rn→R;h(x):Rn→Rm

利用罚函数的无约束优化[12]转换为：

|hi(x)|2/2

(12)

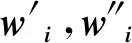
(13)

(14)

解析法求解L(wi,λ,σ)，直到Ll极值点。鉴于ALM算法对初值敏感的问题，需要对原算法进行改进，以减少初值调整重复计算。在迭代过程中做如下变动，因指标评定的绝对误差范围只需要控制在0<εabs≤0.001，0<εrel≤0.01，且存在Hessian构造矩阵正定[13]，对σ可以用样本协方差确定基本罚因子系数，于是令μl(k+1)=μl(k)+2σgl(wi)，按照梯度优化选择法[14]求解：

k∈迭代数

(15)

其中，

(16)

3.2 算法过程

根据上节公式要求，设计求解最小权值wi过程：

Initial(σ,μ0,Numiteration,εabs,,εrel…);k=0;

While (||σ(k)||2>εrelor||s(k)||2>εdual) andk<=Numiteration

{Comp(wl,λl,fk+1(wl),gl(wl),s(k+1),μl(k+1),σ(k+1));

for(l=1;l<=m;l++)

if min(d) then update Dismin,wi; }

alteration(σ,μk+1,Lσ+1,…);

k++;}

3.3 收敛性验证

3.3.1收敛参数

根据条件，ALM有解需要满足f，g为闭区间凸函数，增广函数Lσ闭区间上至少有一个鞍点；在约束中，|f|，|g|无需满秩，则目标函数收敛，对最小距离计算与约束条件组合的进行参数限制，以实现上述要求。通过证明让约束违反值σ及λ大于各自计算阈值，则函数收敛[15]，这样以改进验证相似度Pearson相关系数的倒数作为惩罚系数σ实现差异性修正：

(17)

为保证快速收敛，只需要满足迭代逐渐下降到s(k)≤εdual对偶残差与σ(k≤εabs累计误差则结束，即已知wi,λ,σ0，计算：

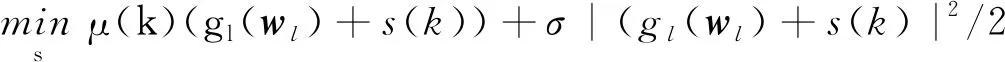
s*(k)=max{0,-(μl/σ+gl(wl))}

(18)

3.3.2验证测试

根据以上要求，在不同λ条件下，检验函数L(wi,λ,σ)多次迭代后的最优解和收敛情况。

表2 不同初值λ下最终收敛极值统计表

通过试验可知，对不同样本，当λ<0.003，L收敛，但是收敛之后还会在误差周围出现震荡，当λ>0.05，整个函数收敛困难，在0.003<λ<0.05时，函数正常收敛。根据统计，在0.004 5≤λ≤0.005 5区间，可以保证良好的快速收敛性。

为考察不同算法对指标参数的评估效果，统一初始参数，设λ=0.005，分别用不同算法对评估样本测试wi的确定情况(见图2和图3)。各20次运算，取平均结果，从图2和图3可知，在已知λ,σ的前提下，标准ALM算法可以获得快速收敛，但因其对乘子λ敏感问题，需要进行更多的样本与参数测试，而交替方向乘子算法(alternating direction multiplier method, ADMM)采用交替梯度求解[16]，实际收敛速度最慢，而本文改进的ALM算法是将二者优势结合起来，先对所有样本提前做归一化处理限制异常样本，利用改进相似度系数σ控制c|h(x)|2，以满足评估要求的误差参数，简化极值计算，实现更快的梯度下降计算，以获得更优的收敛速度，并避免对初始值的过多调整，保证了算法的通用性。

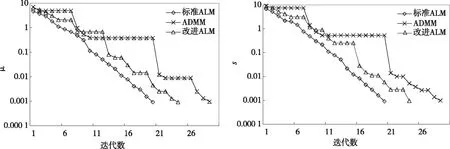
图2 迭代μ收敛情况变化 图3 迭代残差系数s收敛情况变化

4 试验与分析

4.1 权重算法分析

根据高等学校数字校园建设规范体系要求，重点建设顺序为：基础设施优于业务平台优于业务应用优于资源建设优于保障体系优于安全体系，分别选取比较有典型或主流的评估确定权值算法进行比较。在统一问卷与指标系数情况下，分别计算1级指标的权重，根据计算结果得图5:

从图4可以看出，直接的多层次模糊算法指标波动就会明显影响评判结果，不利于评估要求的随时变动；熵权法权重波动明显，其评估准确性有待进一步考查，经典的AHP+CRITIC组合方法[17]评估效果有所改善，但结果波动性大；遗传算法的效率有一定提高，但是因需要大量的训练样本，对应当前高校迅速升级变化的环境，需要经常性的加以训练，影响效率，而本文采用的主客观组合优化算法，具备更好的评估准确性与计算效率结合。

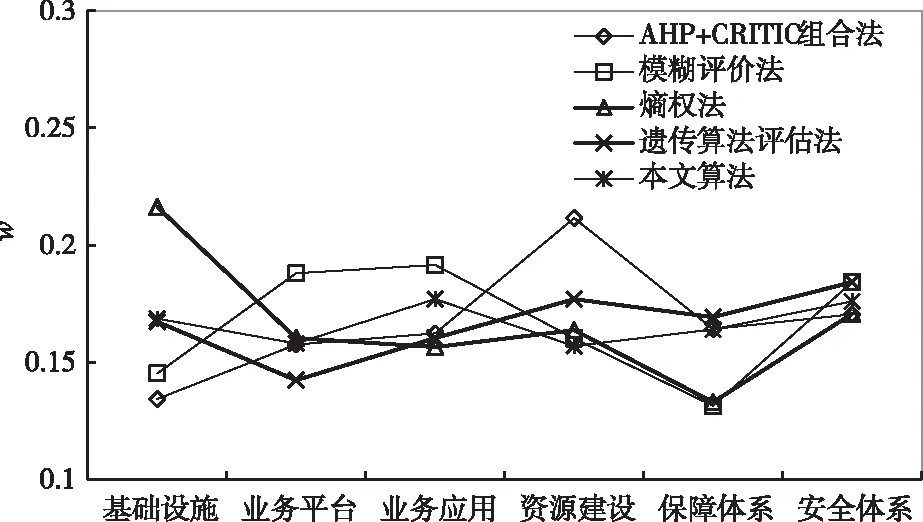
图4 各种权重算法对比图

4.2 智慧高校评估测试

根据2节、3节算法计算本校4年来有大数据评价样本的1级指标权值，得表3：

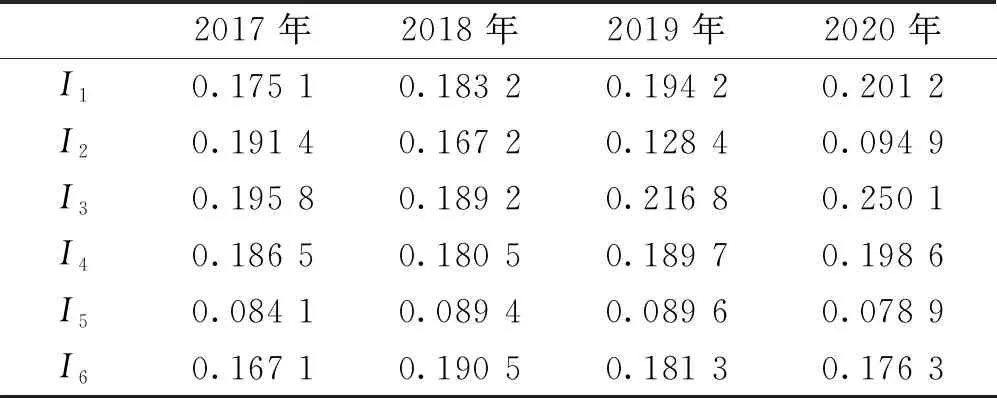
表3 历年1级指标组合权值计算表

(19)

根据公式(19)获得表4和图5:

表4 智慧校园历年评分比较

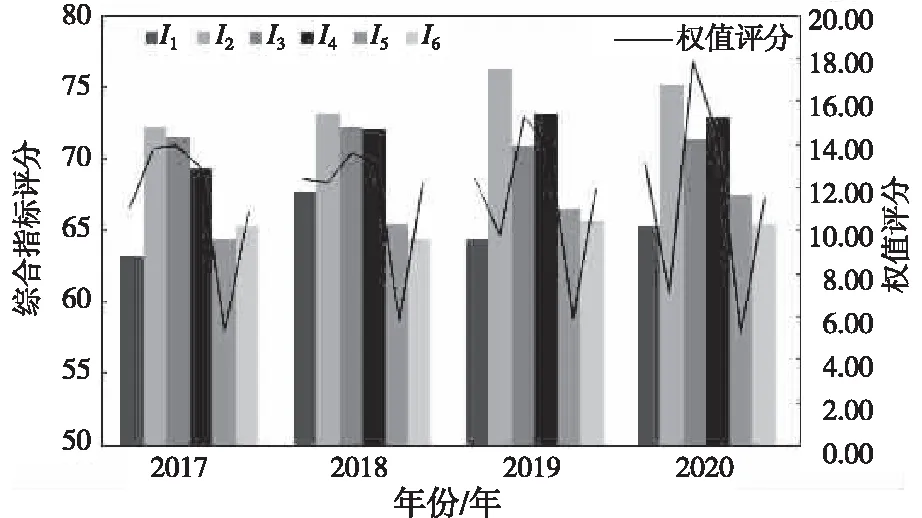
图5 本校2017—2020年1级指标综合评估与权值评分曲线图

根据安徽省教育厅颁发的指标体系获得的综合评分，结合本校4年来信息化建设的已知经验与成果，和图5比较分析可以看出：(1)4年来，本校在设施建设方面的投入，对名义指标有一定提高，但是结合其他关联因素影响，整个评分并未获得同步增长；而在信息支撑方面因操作环境的改善和课程建设的发展，评分却获得持续提高，但其增长趋势却随时间的延续而放缓，这意味着如果要保证智慧校园建设效果，必须考虑在支撑系统中做长期持续的调整或投入才是本校未来智慧化建设的工作重点。(2)在信息应用与数据资源方面，虽受量纲影响，但因权值的变化，总体未见明显提高，体现了组合权重算法的意义；而对保证和维护系统，在组合权重的调整，可以明显体现在4年工作变化的等比例关联，进一步验证了对信息化建设评估可以体现本校对安全建设与运维体现的具体工作可以使用权重加以呈现。

总之，该组合优化算法评估系统体现了智慧化高校建设成果与内涵，可以作为智慧高校评估系统的有效工具加以应用与推广。

5 结语

目前高校智慧化评估技术仍处于初创阶段，本文通过利用大数据信息获取，建立指标评估体系；采用适应评估量化的模糊层次模型与反映主客观因素的变异系数法获得初始权值，并利用改进的ALM组合优化算法以强化部分关键指标。接着通过试验验证算法的收敛性，再根据计算验证本校历年智慧校园建设状况，进一步检验本评估算法的可行性与实效性。总之，该评估方法通过试验验证，证明是一套可行的智慧高校优化评估手段，值得推广。