基于ATM交易特征参数的二重故障检测

窦梓豪 陈俊霖

（重庆邮电大学先进制造工程学院 重庆市 400065）

1 引言

银行ATM 机器在处理业务请求时，前端与客户交互，采集请求信息，后端接收信息，通过网络传输到总行数据中心处理系统。商业总行数据中心监控系统每分钟对各分行的交易业务量、交易成功率、交易响应时间三个指标进行汇总统计，用于捕捉前端和后端整体应用系统运行情况并及时发现异常或故障。

2 数据处理与分析

2.1 数据预处理

根据某商业银行所给出的部分数据进行分析，数据分为日期、时刻、交易量、成功率、响应时间五种数据，其中针对日期、时刻又构成了时间序列数据[1]，由于存在数据较多且关联性不明显，故进行数据预处理：利用SPSS 软件将四位日期、时刻数据创建虚拟变量得到以天数和分钟数升序等差排列后的时间序列；通过缺失值分析选取1月11日到4月10日共计90 天，每天共计1440 个有效数据。

2.2 时间序列提取

运用SPSS 软件的相关性分析功能，得出五种数据分别对应的皮尔逊相关系数和显著性统计值。根据相关性统计表，可以得出时刻与交易量之间相关性较大达0.3703，根据显著性统计，可以得出在99%的置信区间上可以拒绝原假设，即在99%的置信区间上认为皮尔逊相关系数显著的异于0，即时刻与交易量两个指标相关性显著，将交易量与时刻的关系反映到每天的时间序列数据中可得日期-时刻-交易量三维时间序列图如图1 所示，其中每日交易量与时刻间呈双峰正态分布关系[2]。

通过MATLAB 将同一日的交易量数据进行累加求得日总交易量，由图2 观察可得第10 天至第20 天部分几日的日总交易量数据明显与其他日的交易量数据相差较大，且不同日交易量间存在较大落差，通过对原始数据对应的日期进行查询可得，图中高峰日期对应时间在2017年为农历春节期间左右，实际情况中存在春节前夕大量存取钱高峰，导致ATM 机交易记录剧增剧降。

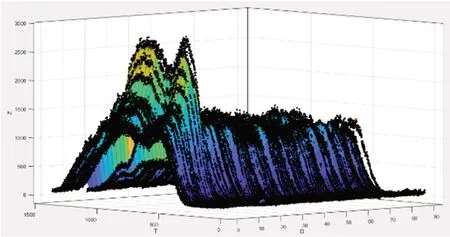
图1：日期-时刻-交易量三维时间序列图

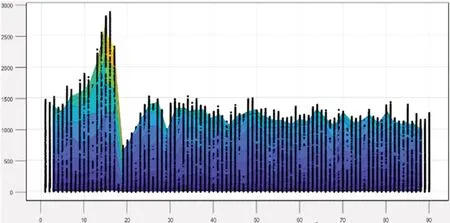
图2：日总交易量统计图

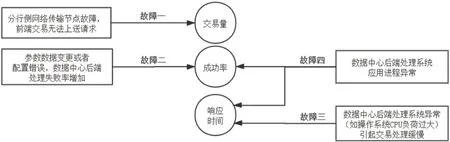
图3：指标-故障映射图

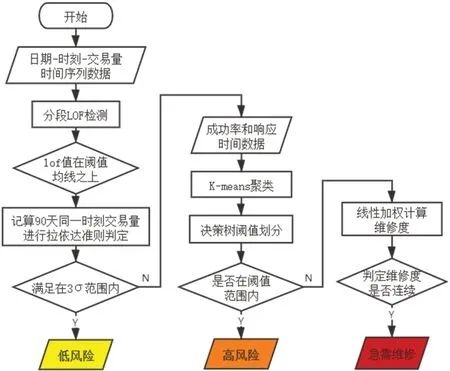
图4：故障检测流程图

为了方便后面的研究不受影响，采用系统层次聚类分析更准确的将日期进行分段处理，根据系统聚类图谱分析可以分为：

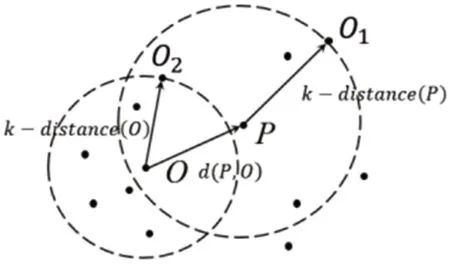
图5：可达距离示意图

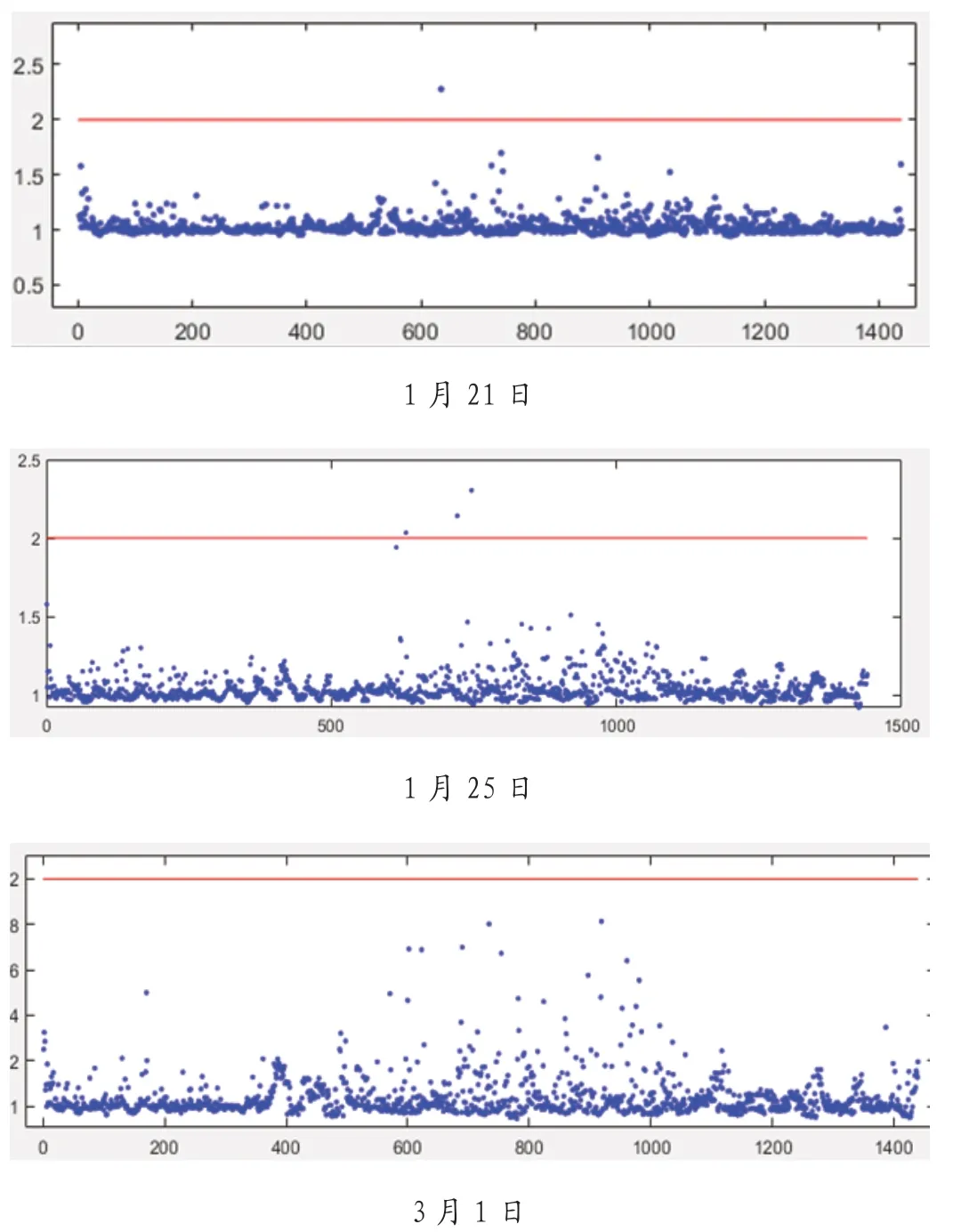
图6：离群值

（1）第1～12 天，即1月11日～1月22日；

（2）第13～16 天，即1月23日～1月26日；

（3）第17～90 天，即1月27日～4月10日。此聚类结果将交易日期分为三段进而进行研究ATM 机交易状态的特征参数。

3 二重故障检测模型的建立与求解

3.1 模型的建立

由背景资料可得，四种常见的故障场景又对应于总行数据中心监控系统统计的业务量、交易成功率、交易响应时间三个指标，由机理分析可得其映射图如图3 所示。

针对四种故障和三种数据指标，首先提取ATM 交易状态的特征参数，进而代入故障检测模型中逐级进行故障判断。

对交易量数据采用的特征参数为离群因子[3]。利用离群因子对同一天不同时刻以及不同天同一时刻的交易量随时间变化的数据点进行刻画，将达到LOF 阈值的数据判定为一次异常值，然后进行拉伊达3σ 原则判断，不满足的列为二次异常值。

表1：二次异常值数据

表2：三段聚类中心坐标表

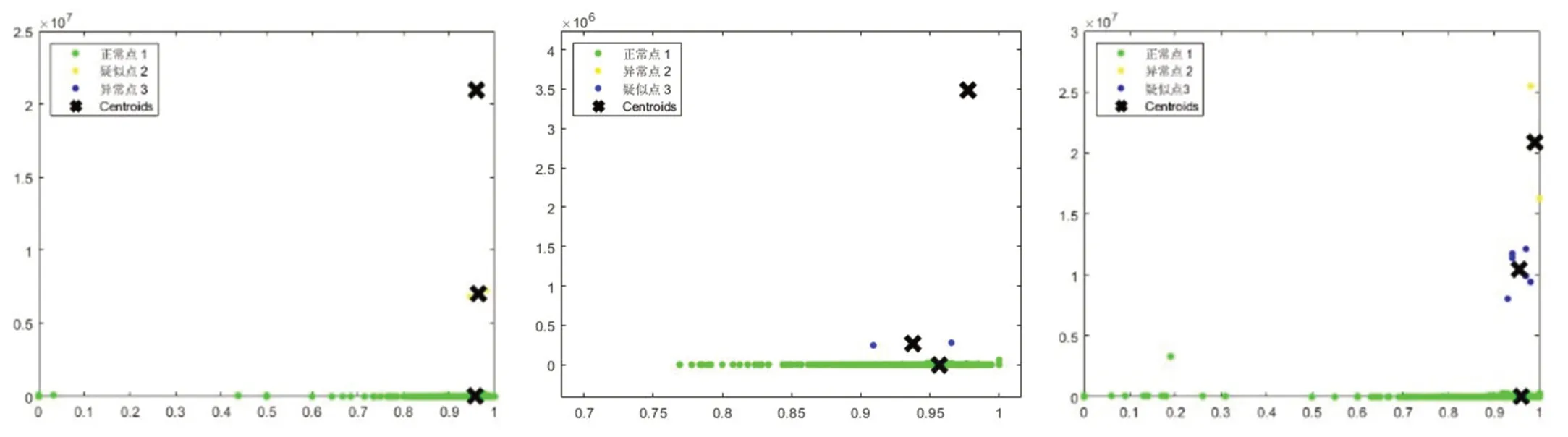
图7：春节前、中、后各段聚类图

对成功率和响应时间数据，利用K-means 聚类与决策树提取聚类区间阈值作为特征参数[4]。利用80%数据聚类与决策树划分的阈值作为指标，同时用20%数据对决策树结果进行检验。将一次、二次异常值带入分段聚类中心再次判断成功率与响应时间是否异常。

通过LOF检测出的一次、二次异常值和聚类中心划分的正常点、疑似异常点、异常点进行对应，最终按照故障检测标准符合两类判断条件情况得出低风险、高风险、急需维修，实现故障情况以及对应的预警等级的判断。故障预警流程图如图4。

3.2 LOF算法介绍

LOF（Local Outlier Factor，对象的局部异常因子）算法中每个数据都被分配一个局部异常因子，局部异常因子愈大，就认为它更可能是一种异常；反之则可能性小。计算局部异常因子，先产生所有数据点的k-邻域（同时得到k-距离），并计算到其中每个点的距离。算法流程如下：

（1）计算对象p 的k-距离。

对任意的自然数k,定义p 的k-距离（k-dis(p)），为p 和某个对象o 之间的距离，此时o 满足：至少存在k 个对象使得并且至多存在k-1 个对象使得

（3）计算对象p 相对于对象o 的可达距离。

给定自然数k，对象p 相对于对象o 的可达距离为：

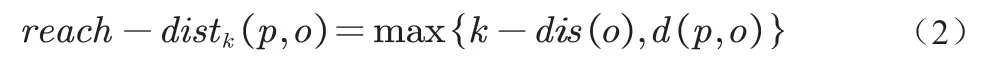
（4）计算对象p 的局部可达密度（Local Reachable Distance）。

对象p 的局部可达密度为对象p 与它的k-邻域的平均可达距离的倒数。

（5）计算对象p 的局部异常因子：

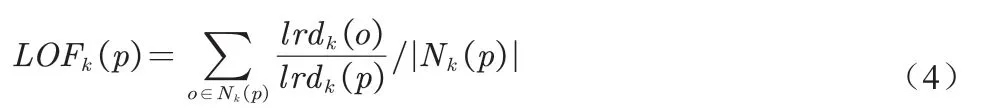
3.3 LOF算法求解

利用MATLAB 依次将每一天每个时刻的交易量数据进行LOF处理，LOF 检验离群点需要确定k 值，k 值取太小会使得平缓部分的一部分疑似异常点被当成正常点，k 值取太大又会使得上升下降阶段时 LOF 值较敏感，经过k 取值的分析对比，采用k=5 作为邻近对象。一般情况下，认为异常因子接近 1 的点，说明它和周围点的密度一致，判定为正常；异常因子越小说明它和周围点的密度相差越大，因此，成为异常点的可能性也就越大。

表3：故障检测标准

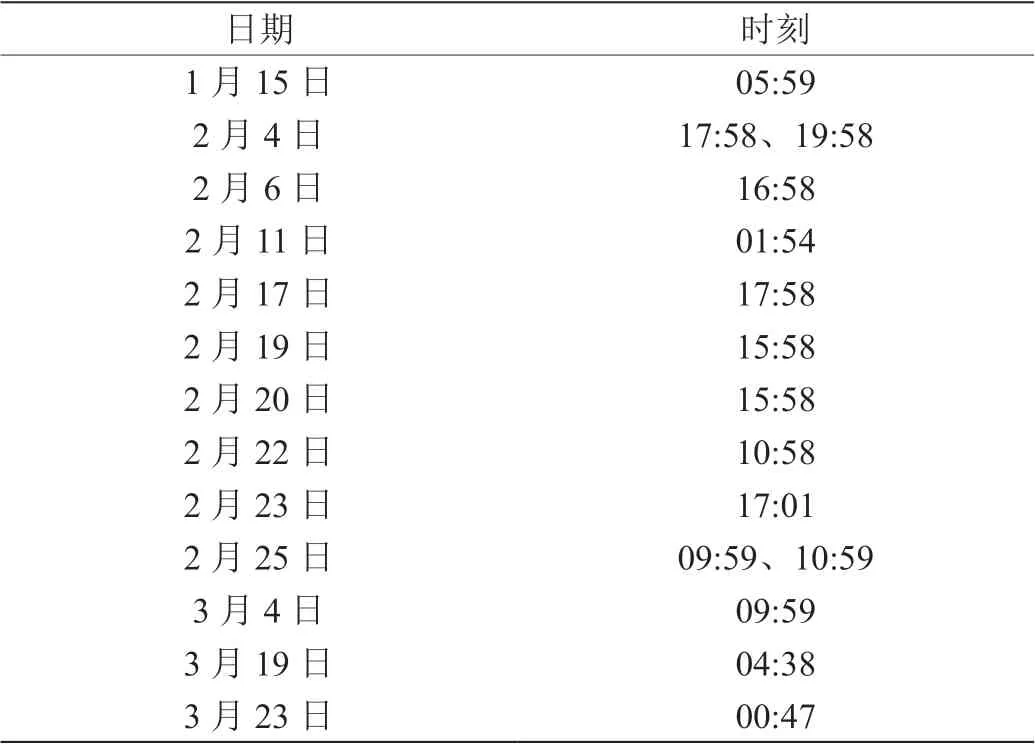
表4：最终故障维修点

根据本题日交易量的数据分布特点，将 LOF 阈值设定为2，即满足：

视为一次异常值，分别选取每段日期内的一天离群因子观察情况，即以第10 天（1月21日）、第15 天（1月25日）、第50 天（3月1日）为例，作出其每一时刻的离群值图像如图6 所示。

3.4 拉伊达3σ准则

找到对应一次异常值的日期和时刻，按照三个分段日期，对90 天数据中与一次异常值在同一时间段的每天对应时刻数据进行统计，计算其标准差和均值，再将达到离群值阈值的数据进行拉依达3σ 检验，采用数值分布在（μ-σ,μ+σ)中的概率为 0.6826 作为正常情况，如果LOF 检验出来的一次异常值在（μ-σ,μ+σ)区间内，则仍然可以作为正常点来处理，如果不符合拉伊达σ 检验的异常点则被认为是二次异常值，用于下一步成功率与响应时间的检验。其中，考虑到实际情况中每台ATM 机在每日凌晨左右会进行一定的设备升级或者定期维修，也存在有加钞时机的影响，所以将每日异常数据属于23:50—00:10 的数据直接进行剔除，避免实际情况影响到模型分析。

最终二次异常值检验结果如表1 所示。

3.5 K-means聚类分析

由指标-故障映射图可直观得出：故障三数据中心后端处理系统异常（如操作系统CPU 负荷过大）引起交易处理缓慢，影响交易响应时间指标，以及故障四数据中心后端处理系统应用进程异常，导致交易失败或响应缓慢均能够直接或间接影响到交易成功率和响应时间，通过SPSS 软件对每一时刻的交易成功率与响应时间进行K-means 聚类分析。

传统 K-Means 算法的基本思想是初始随机给定K 个簇中心，按照最邻近原则把待分类样本点分到各个簇。然后按平均法重新计算各个簇的质心(这个点可以不是样本点)，从而确定新的簇心。迭代到到簇心的移动距离小于某个给定的值。因此下文根据点的分布来确定其聚类中心，增加其稳定性。按照时间分段分别作出春节前、春节期间、春节后三段时间每一时刻下的交易成功率和响应时间聚类分析图（图7）。

图7 中绿色、黄色、蓝色分别对应各自时间段内的正常点、疑似点、异常点。春节前阶段1月11日-1月22日。取12 天数据作为训练集交易成功率整体较高，响应时间整体较低，聚类之后可得第一类与第二类都属于正常点，第三类作为疑似异常点进行下一步的判断；春节阶段1月23日-1月26日取了4 天的数据作为训练集。数据特点是平均交易量偏高，从成功率与响应时间来看，第一类与第二类都属于正常点范围，第三类属于异常点。春节后阶段1月27日-4月10日一共有64 天数据是较为明显分为了三类，将其归纳为正常点、疑似异常点、异常点。如表2 所示。

3.6 故障检测结果

通过回溯表1 中的57 个二次异常值寻找同时又满足落在对应聚类中心区间内的值，结合离群值特征参数和聚类中心参数进行线性加权并判断原始数据点处其异常值情况是否连续，可以得出最终的交易故障检测标准如表3 所示。

当满足交易量是LOF 二次异常值，并且该时刻的交易成功率和响应时间满足聚类中心异常点范围内，该时刻ATM 交易状态的特征为：前后几分钟交易量骤降，交易成功率较低并且交易响应时间较长，存在暂缓性异常而非即刻性异常，与实际情况相符。最终统计所有急需维修结果，得出最终故障维修点如表4 所示。

4 小结

本文针对ATM 机交易故障情况与三种交易指标间建立起映射关系，并将日期时间按照实际春节前后进行分段提取特征参数，通过二重故障检测模型逐步筛选异常值、故障点，最终得出故障风险等级，通过验证，模型检测结果符合实际情况，模型可供后续故障预警运用。