基于激光雷达的停车场车辆定位算法

周 苏，李伟嘉，郭军华

（1.同济大学汽车学院，上海 201804；2.同济大学中德学部，上海 201804）

汽车定位是汽车自动驾驶的核心技术之一，也是实现环境感知、路径规划与控制等后续功能的基础。目前汽车定位采用的传感器主要有激光雷达、毫米波雷达、惯性测量单元（IMU）和摄像头。在室外空旷无遮蔽的道路环境下，基于GPS+IMU的定位导航方法已经可以保证较高的精度［1］。L4以上级别的自动驾驶要求厘米级定位精度，目前最有前景的技术方案是基于GNSS（global navigation satellite system）+IMU+lidar/camera+高精地图的融合定位。例如，谷歌的激光雷达定位方案、斯坦福大学的概率地图点云匹配定位方案［2］和特斯拉的视觉定位方案。无论是基于激光雷达的还是基于视觉的定位系统，其基本思路都是基于环境要素的匹配对汽车进行定位，即事先利用采集车采集高精地图数据，然后用实时扫描特征（激光或视觉）与事先制作的高精地图匹配，最后获取车辆的位置估计。因此，即使在室内环境如隧道、停车场等情况下，车辆无法获取可靠的GPS信息，也可以采用其他传感器信号进行定位。毫米波雷达无法得到大量的环境点云信息，目前主要在ADAS（advanced driver assistant system）中用于距离探测［3］。基于摄像头的视觉SLAM（simultaneous localization and mapping）算法目前在一些室内机器人中有所应用，但是其累积误差较大，会发生定位漂移。在较大的环境尺度如停车场内，即使增加闭环检测措施，漂移情况也十分严重，视觉SLAM算法用作车辆主要定位方案的可靠性较低。激光雷达可以获取大量的环境点云信息，已经越来越多地被用于三维环境重构和机器人定位以及无人驾驶建图定位等领域［4］。

激光雷达的自主定位可分为建图和定位2个步骤。较早的研发中建图主要通过卡尔曼滤波器等方法实现，较近的研发中已经逐步采用基于非线性优化的SLAM算法，即同时定位与建图的方法。目前较为流行的激光雷达SLAM算法开源框架主要有ROS（robot operating system）中集成的Gmapping、Karto-SLAM、德国达姆施塔特工业大学提出的Hector-SLAM和谷歌开发的Cartographer-SLAM等。为了在较大尺度的室内环境中研究激光雷达SLAM，以某一100 m×50 m的测试停车场为例，基于Cartographer框架开展相关的优化工作。

根据SLAM算法得到环境地图后，在车辆运行过程中就可以实现实时车辆定位。车辆定位算法的实质是一个状态估计问题，一般分为状态预测与修正2个步骤。首先根据状态转移方程预测状态的当前估计值，然后根据当前的观测模型修正状态的估计值，状态估计就是不断地重复状态预测与修正的过程。卡尔曼滤波器和粒子滤波器是状态估计常用的2种算法。本研究中采用粒子滤波器进行车辆位姿的估计，得到车辆位姿的最大似然估计［5］。然后，结合KLD（Kullback-Leibler divergence）采样方法，动态控制采样粒子样本数。

1 SLAM算法构建地图

1.1 概率占栅格地图模型

选择概率占栅格地图模型［6］用于车辆定位。占栅格地图实际上是环境信息的一种离散描述，即根据分辨率将地图划分为小栅格，地图M就是所有栅格mp的集合。如果用1或0表示栅格是被占据的或未被占据的，那么ρ(mp=1)（简写为ρ(mp)）就代表着这个栅格被占据的概率。地图M表示如下：

概率占栅格地图M的取值被限制在[ρmin，ρmax]之间，表示栅格被占据的概率。每个栅格在作为图片显示时，也是一个像素。当每一帧激光雷达扫描数据被插入到概率栅格中时，都有一组表示命中与一组表示未命中的点集被计算。如果命中，就将最接近激光雷达扫描点的栅格加入到命中点集中。如果未命中，就将激光雷达扫描的原点与命中点连线，将连线上所经过的栅格都加入到未命中点集中。如图1所示，命中点所在的栅格用打叉的灰色格子表示，未命中点所在的栅格用不打叉的灰色格子表示。白色栅格表示未知，即尚未被探测到的区域。

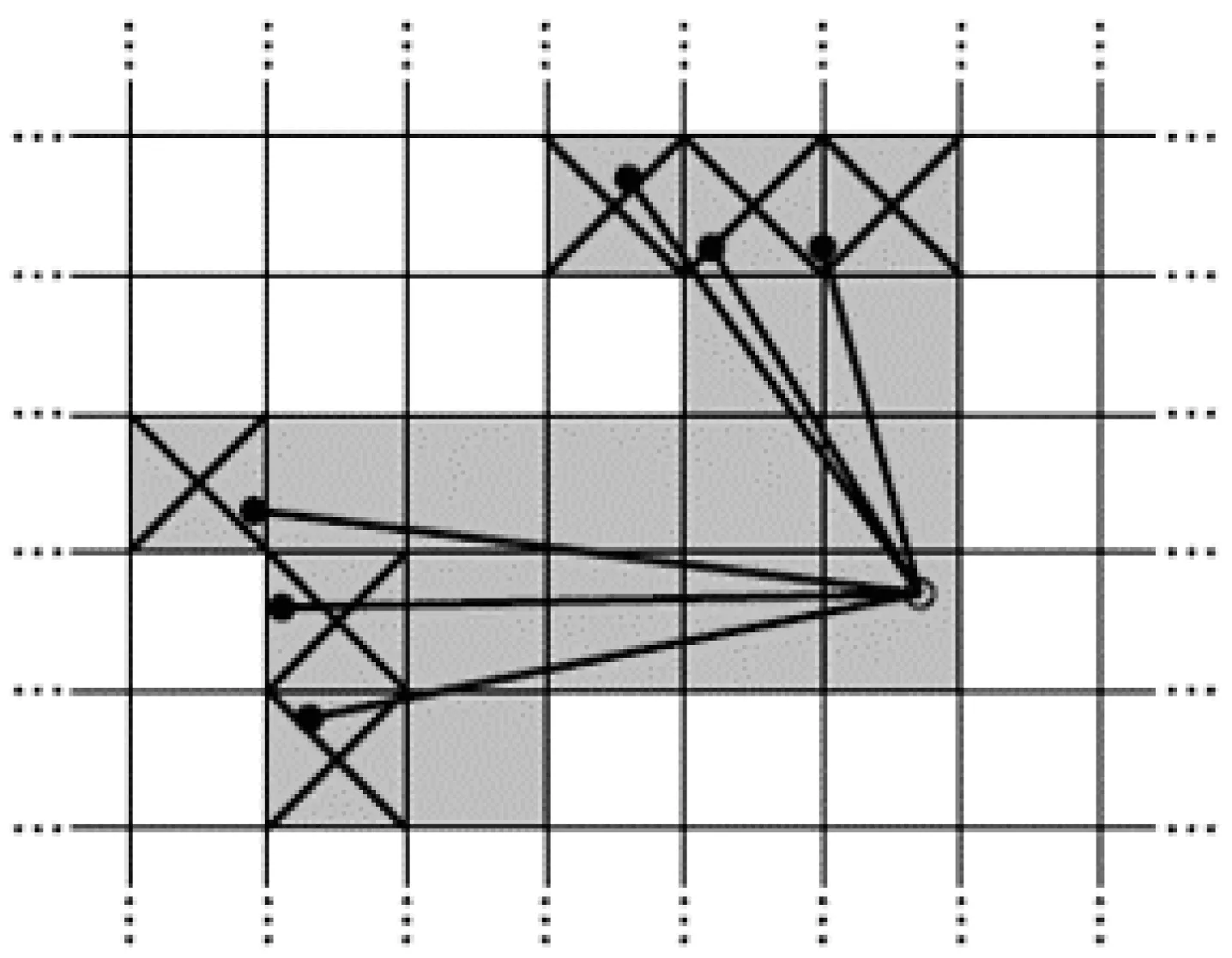
图1 概率占栅格地图模型［6］Fig.1 Probability grid map model[6]

网格中每个栅格被占据的概率ρ(mp)不是由一次扫描决定的，而是由经过该点的多次扫描共同决定的。对于之前已经观察过的栅格，如果处于命中或者未命中的点集中，将会被分配到一个占据概率ρ。对一个之前已经观察过的栅格，可通过下式更新它的命中率与被占据概率［7］：

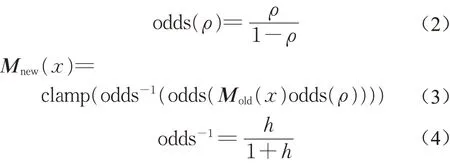
式中：odds表示命中率函数，odds-1表示命中率函数的反函数；ρ表示栅格被占据的概率；Mold、Mnew分别表示更新前、更新后的地图；h表示命中率；clamp表示极值限定函数，可以将函数结果限定在给定的最小值与最大值的区间中。

1.2 激光雷达前端点云匹配

SLAM通常分为前端和后端，前端主要充当里程计的角色，通过2帧激光雷达数据之间的相对变换确定车辆的位姿。通过旋转和平移将2帧激光雷达数据进行最大限度的重叠，就可以得到车辆在2帧数据之间的相对位姿变化。

现在的激光雷达SLAM一般不直接进行2帧数据之间的点云匹配，这是因为直接点云匹配计算量太大、耗时太长，而且匹配结果的误差较大、漂移严重，不利于后端的位姿优化。因此，一般使用激光雷达数据与当前构建的子地图Submap进行匹配［7］。激光雷达位姿的变换可用下式表示：

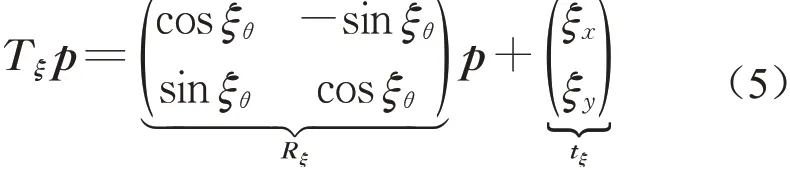
式中：Tξ为坐标系的变换矩阵；Rξ为旋转矩阵；tξ为平移矩阵；p为当前扫描数据中各个点云的坐标；ξ为激光雷达坐标系与子图坐标系之间的相对位姿。激光雷达数据与子图之间的匹配可以通过构造一个非线性最小二乘问题得到解决，相应的目标函数如下所示：

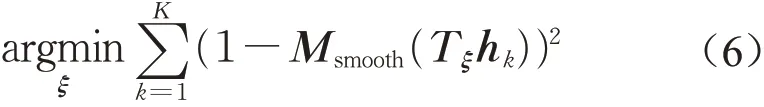
式中：K为一次扫描数据的点集总数，k为点集K中的第k个扫描点；h k为第k个扫描点的空间坐标；Msmooth为经过插值处理的概率占栅格地图。概率占栅格地图本来是离散的，为了保证式（6）在进行迭代计算时能够稳定且收敛，需要通过插值处理来生成光滑的概率地图。选用双三次插值方法进行处理，产生的地图更加平滑且稳定，同时插值后可能出现概率小于0或者大于1的情况，但这种情况不会产生错误也不会影响计算。高斯-牛顿迭代法可以求解式（6）描述的非线性最小二乘问题［8］，同时已有很多开源求解器如Ceres、G2O等可供选用。Ceres库提供了基于模板元的自动求导和运行时的数值求导，只需构建代价函数即可，而G2O库只提供运行时数值求导的一种方式，同时需要构建误差图模型。因此，采用Ceres库［9］进行求解。

某次激光雷达数据与子图间的匹配如图2所示。左侧为匹配前的点云初始位置，即粗配准位姿，右侧为经过式（6）迭代计算后的点云位置。可以观察到，经过高斯-牛顿迭代法求解式（6）后得到的位姿更为精确，这是因为激光雷达点云数据与子图有着更多的重合，如图2中用圆圈标出部分。迭代过程中的车辆位姿（ξx，ξy，ξθ）变化如表1所示。经过约11次迭代后收敛至新位姿，可见通过高斯-牛顿迭代法可以快速对车辆位姿进行精配准。

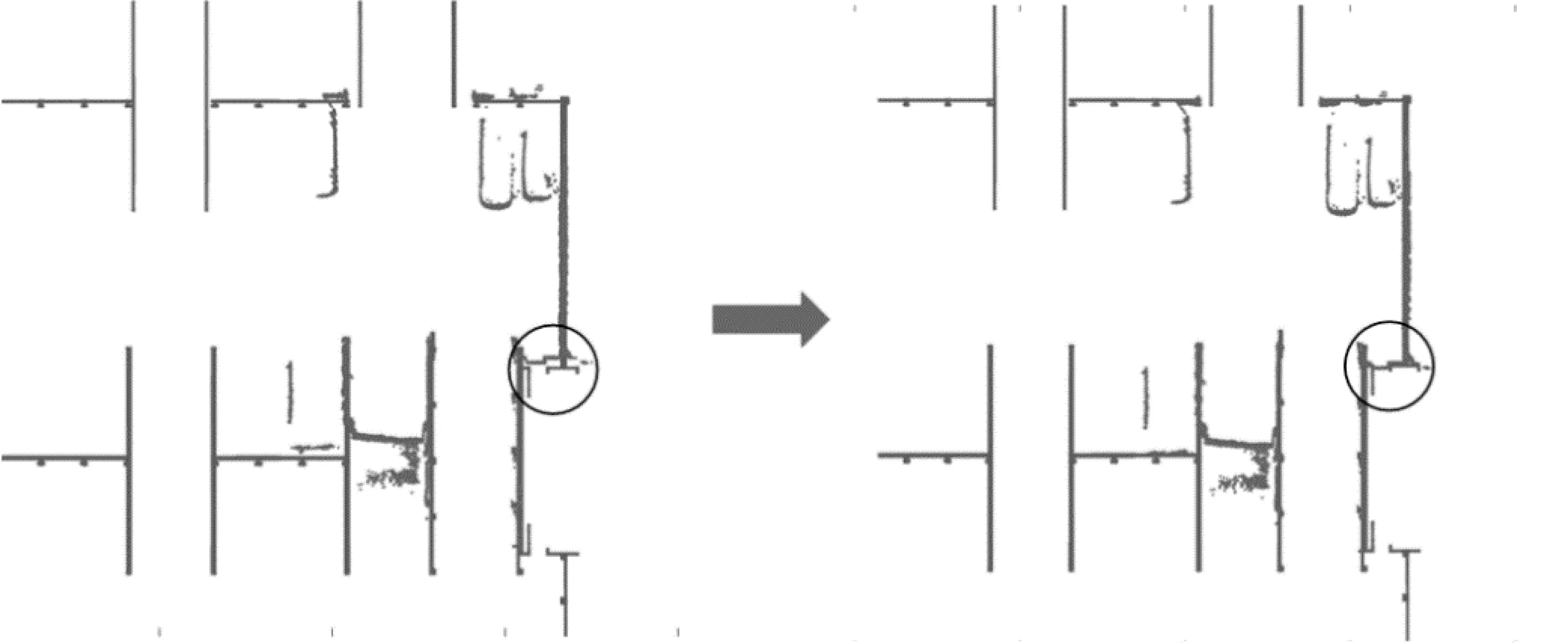
图2 激光雷达数据与子图匹配示意图Fig.2 Schematic diagram of lidar data matching with submap

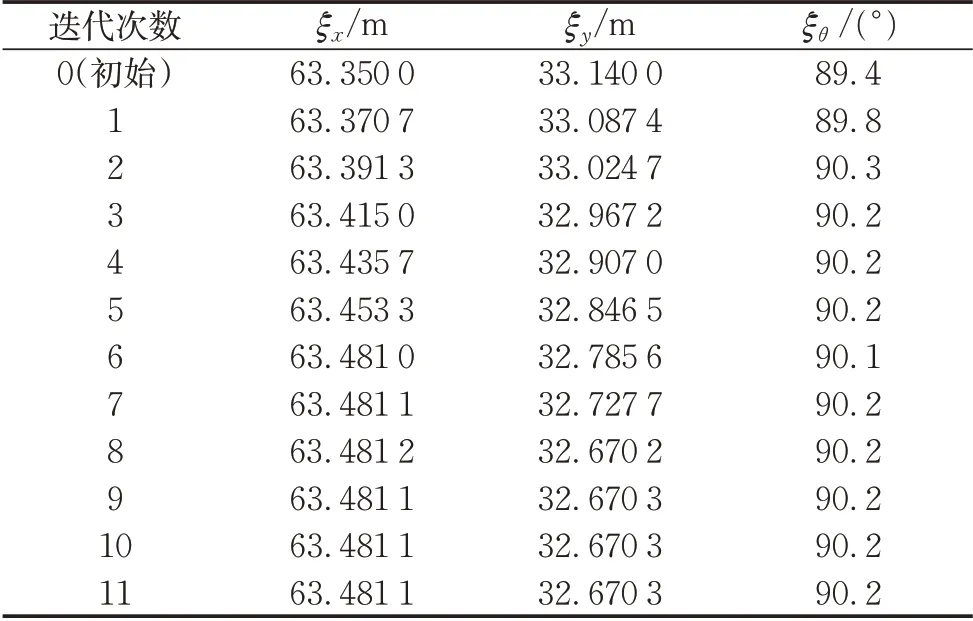
表1 位姿随迭代次数变化Tab.1 Pose changes with the number of iterations

图3为通过精配准后导出的停车场局部三维点云地图。由于使用的是ibeo LUX 4L激光雷达，在垂直于地面方向上只有4条线束，因此无法采集到较高位置的信息，只能获得二维平面地图信息。可以看到，点云地图中的车辆与墙壁受限于激光雷达线束数量，只有很低的高度，因此采用二维占栅格地图配合粒子滤波器用于车辆定位。

图3 停车场局部点云配准地图Fig.3 Local point cloud registration map of parking lot

1.3 基于图优化理论的后端优化

基于图优化理论的位姿调整（在很多文献中也被称为闭环检测）是激光雷达SLAM的核心内容。后端优化用于修正SLAM过程产生的累积误差，提高车辆定位和地图构建的准确度。和前端匹配类似，后端优化也需要构造非线性最小二乘问题，如下所示：

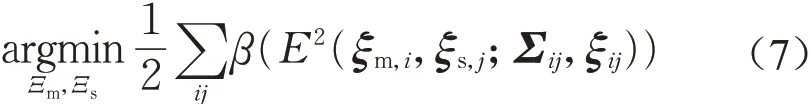
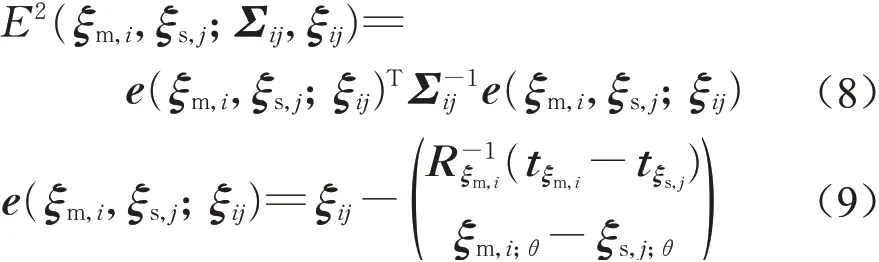
式中：e为误差函数。计算中要用到式（5）旋转矩阵Rξ的逆变换。

图4为一次闭环行驶后未经过图优化调整直接得到的停车场占栅格地图。虽然停车场的局部匹配信息较为精确，但是SLAM过程中有累积误差，导致地图在较大尺度上漂移严重。图5为根据式（7）进行全局位姿调整后得到的停车场占栅格地图。从图5可以发现，累积的全局误差被很大程度地消除了。

1.4 占栅格地图与建筑地图对比

通过前端的点云匹配以及后端的位姿优化就可以绘制出环境地图，但绘制出的环境地图并不能直接用于车辆定位，因为地图还存在少许特征缺失、尺度偏移等现象。同时，静态地图不应该含有环境的动态信息，如停车场中的车辆信息。因此，需要通过多次数据采集来绘制出大量信息完整的地图，再将地图拼接融合，并且剔除环境的动态信息。图6为单次SLAM所绘制的停车场概率占栅格平面地图，可以看到一些环境信息被车辆所遮蔽。

图6 一次SLAM后的停车场占栅格地图Fig.6 Grid map of parking lot after one SLAM

通过多次数据采集并进行信息融合，剔除停车场的车辆信息，补全每次局部采集缺失的信息后，最终得到的停车场占栅格地图如图7所示。与图8对比后可以发现，经过融合调整后的地图能够精确反映停车场的环境信息。

图7 停车场概率占栅格地图Fig.7 Probability grid map of parking lot

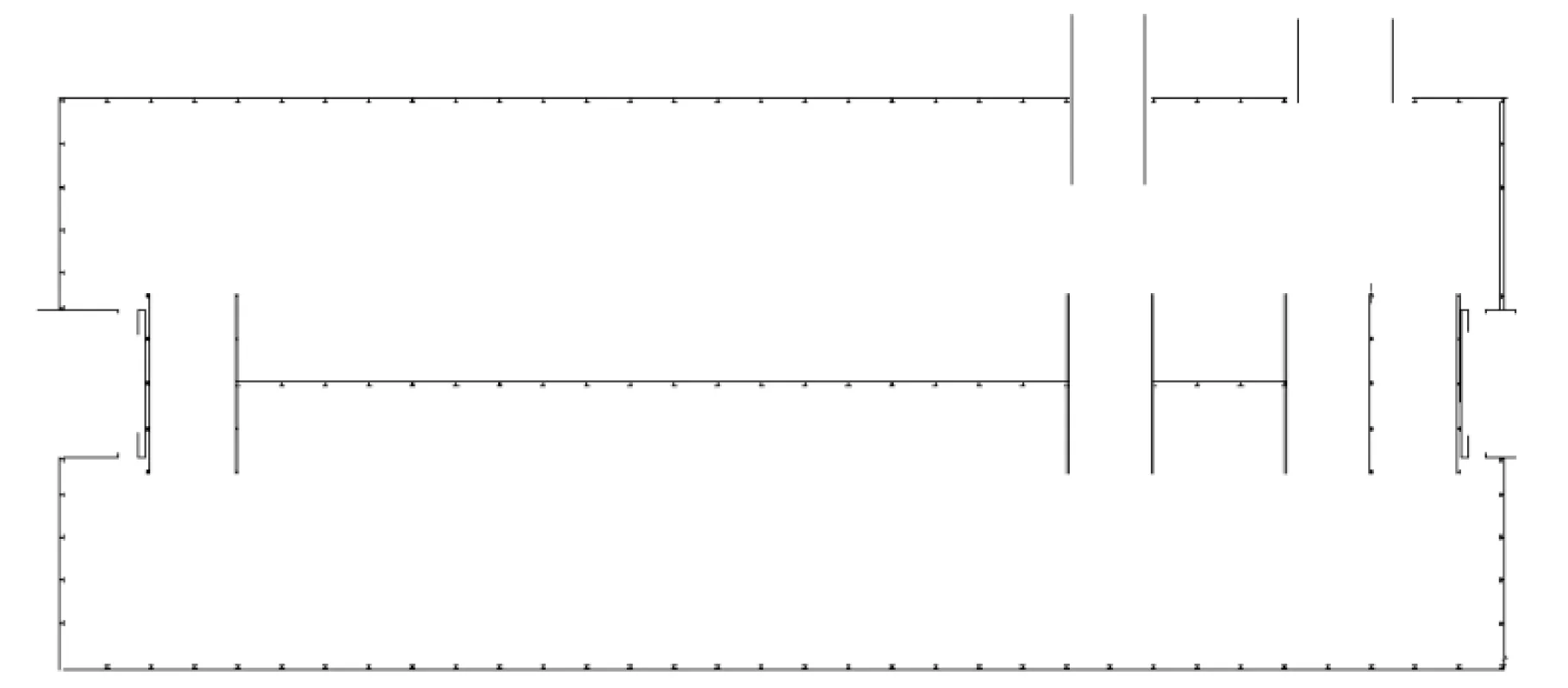
图8 停车场的建筑设计地图Fig.8 Architectural design map of parking lot

2 车辆在线定位

车辆的在线定位通过蒙特卡洛定位方法予以实现。首先，通过运动模型确定车辆当前时刻的先验位姿分布；然后，在先验位姿周围投下大量的带权重随机粒子，粒子的权重代表着该位置与地图的匹配程度，匹配程度越高的粒子就越有可能在重采样过程中被选入后验概率分布的粒子集；最后，通过重采样过程得到车辆位姿的后验概率分布。

2.1 粒子滤波器框架设计

粒子滤波器是通过迭代方式不断更新车辆位姿的后验概率分布，以逐渐消除误差，最终达到精确定位车辆的目的。主要步骤为：①初始化粒子群，生成N个带权重的粒子，每一个粒子代表一种可能的车辆位姿状态；②模拟粒子运动，通过里程计或者激光雷达里程计给出车辆位姿的先验估计；③计算粒子权重，通过粒子与概率占栅格地图的匹配程度给予每一个粒子一个权重，权重越大，表明该粒子越有可能代表真实的车辆位姿状态；④根据粒子权重重采样，权重越大的粒子就越有机会被重采样选中，之后便可以得到当前时刻车辆位姿的后验概率分布。不断地重复②～④就可以对车辆进行在线定位。粒子滤波器流程如图9所示。

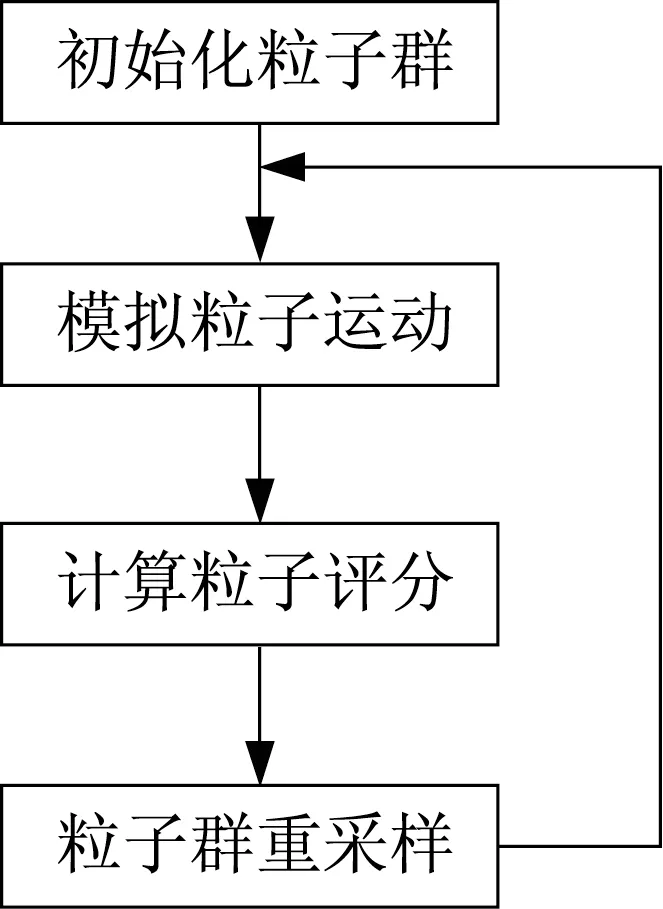
图9 粒子滤波器流程Fig.9 Flow chart of particle filter

粒子滤波器定位的核心就是通过大量带权重的粒子模拟车辆运动，每个粒子都表示一个可能的车辆位姿。图10描述了粒子状态随迭代次数的变化。刚开始定位时，初始位姿来自于GPS信息，此时车辆已经进入停车场，卫星信号遮蔽严重，定位结果不可靠。因此，假定粒子的分布是以初始位姿为均值（0，0）、方差为0.5 m2的二维高斯分布，并以此状态开始粒子滤波器的迭代，如图10a所示。在经过100次迭代后，粒子的朝向已经较为统一，而粒子的位置分布还较为分散，如图10b所示。在经过200次迭代后，粒子基本稳定在位姿均值附近0.5 m范围内，在经过300次迭代后，粒子方向基本一致，位置也更为聚拢，如图10c、d所示。由图10可见，在车辆运动过程中，通过对环境的观测，不断地更新粒子权重以及重采样高权重粒子，以逼近车辆的最大后验估计位姿。

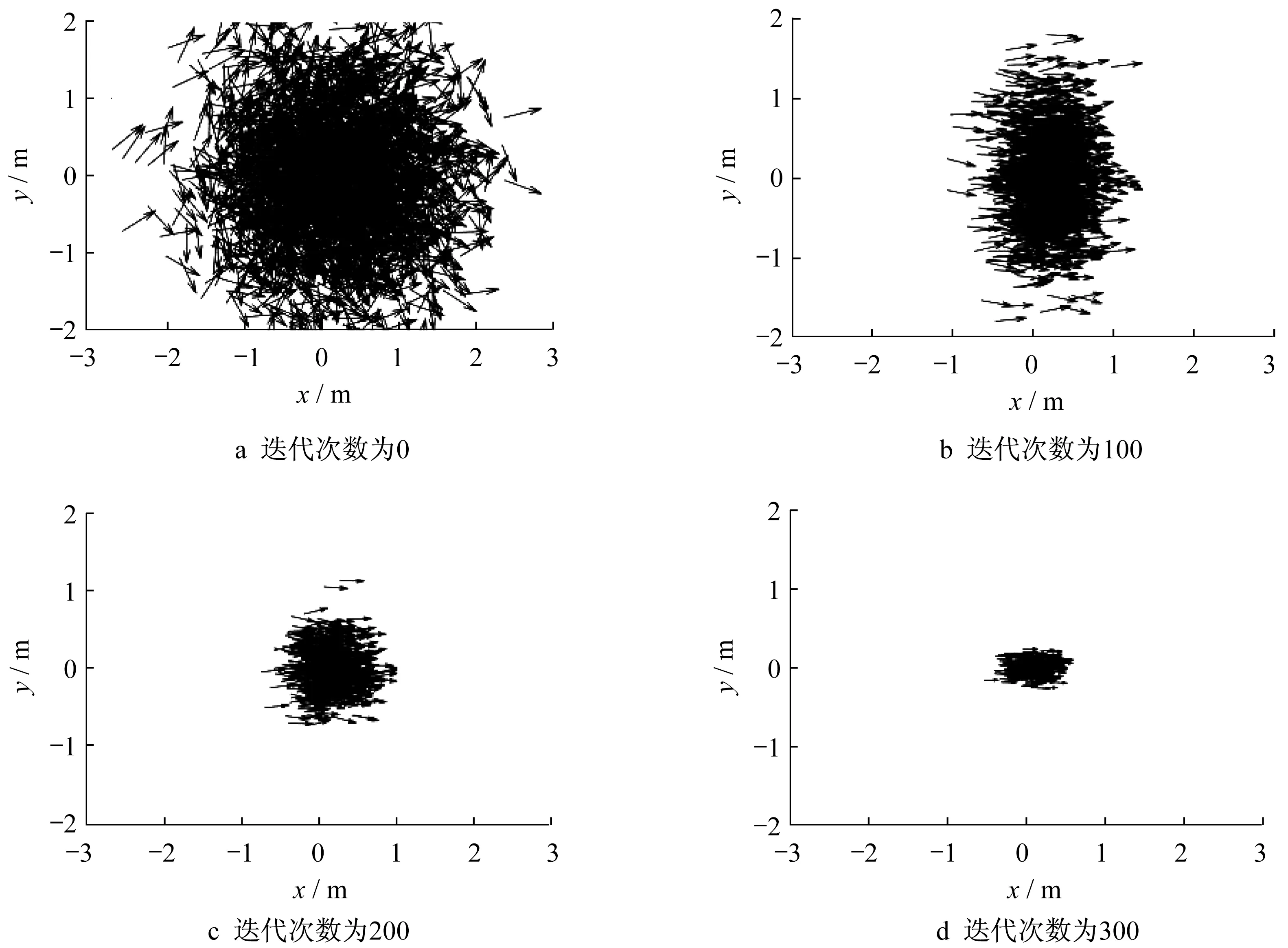
图10 粒子滤波过程中粒子状态变化Fig.10 Changes of particle state during particle filtering

2.2 粒子权重的计算

粒子的权重可以通过计算各个激光雷达扫描点与概率占栅格地图M中处于占据状态的栅格之间的距离和来确定。距离和越小，说明该粒子越能反映真实的车辆位姿，因此权重就越大；反之，距离和越大，粒子的权重也就越小［10］。指数函数可以描述上述关系，如下所示：

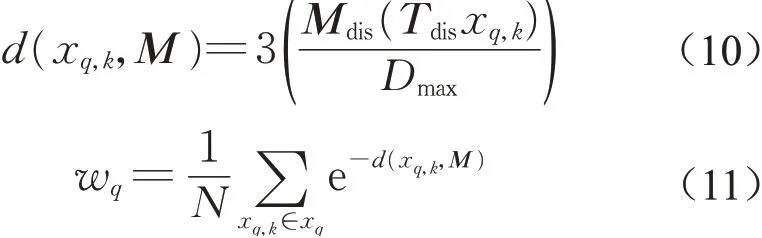
式中：M表示原始的概率占栅格地图；Mdis表示由距被占据状态栅格最近距离组成的二维地图矩阵；Tdis表示激光点云的坐标变换矩阵；Dmax表示Mdis地图矩阵中的距离上限；x q表示第q个粒子扫描得到的所有激光雷达扫描点的集合；x q，k表示第q个粒子中的第k个扫描点；N表示x q中扫描点的总个数；w q表示第q个粒子的最终权重。

图11中，左侧为粒子滤波器在线定位时激光雷达与占栅格地图匹配图，右侧为以车辆估计位姿为中心的4 m×4 m范围内权重的分布结果。权重是重采样过程的重要依据，也是粒子滤波器的核心步骤。权重表征该位置为车辆真实位置的可能性大小，因此权重的分布与车辆周围的环境有着紧密的联系。图11a中，高权重区域集中在垂直于车辆前进的方向上，车辆在该方向上移动时车辆两侧的点云始终与地图中的墙壁重合，因此在该方向上计算出的粒子权重也较其他地方更大。图11b中，高权重区域集中在平行于车辆前进的方向上，车辆进入狭长的廊道时，沿着车辆前进的方向均能保证较高的点云重合度，因此该区域粒子权重也更大。图11c中，权重的分布呈一单峰状，表明车辆在该位置时环境特征明显，利于粒子滤波器定位。

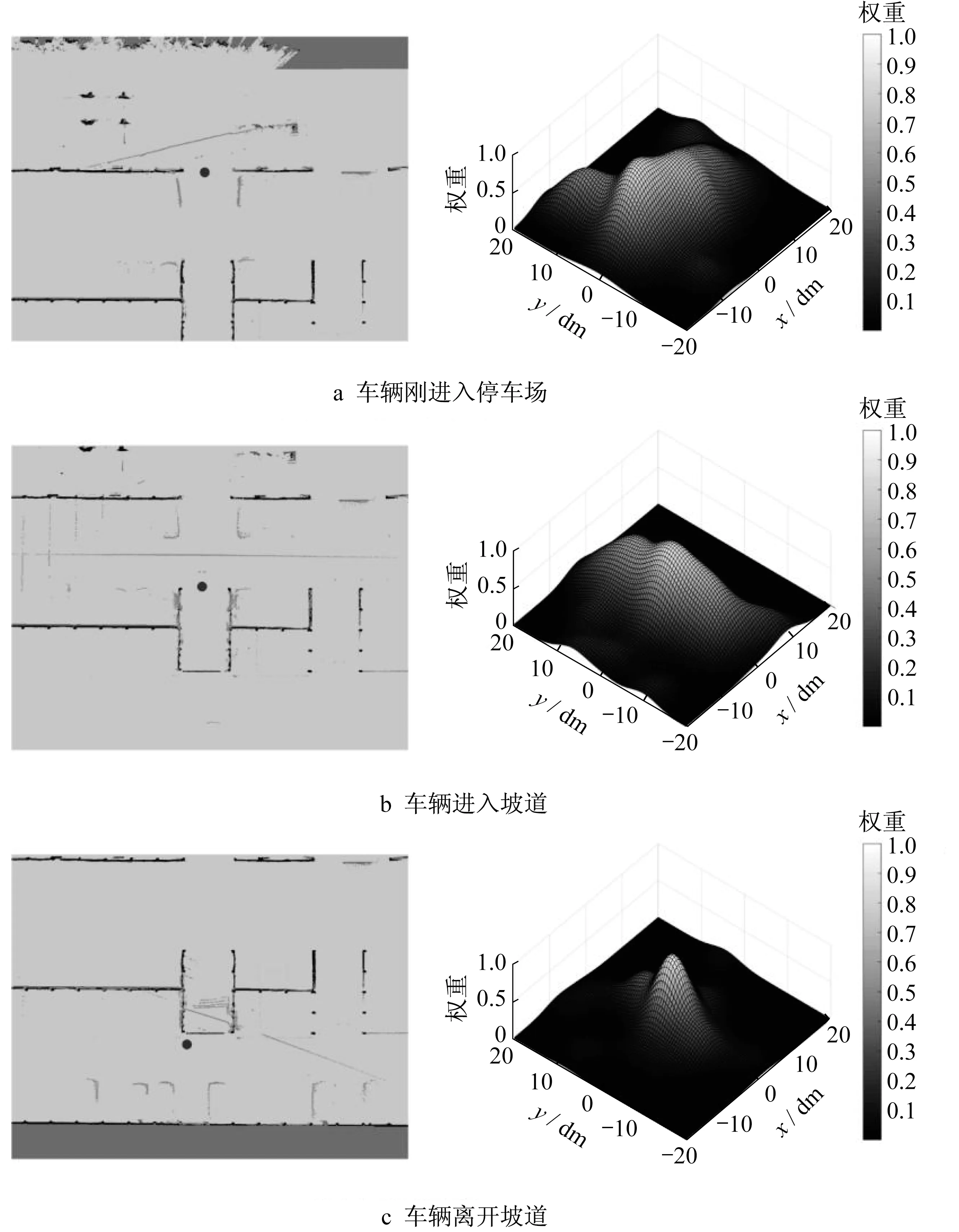
图11 不同位置粒子的权重分布Fig.11 Weight distribution of particles at different positions

2.3 重采样过程

KLD采样是蒙特卡洛定位的一个变种，能够动态地随时间改变采样样本的粒子数［11］。引入KLD采样可以在保证定位精度的前提下，尽量减少粒子数量，进而提高运算效率。通过采样的近似质量的统计界限来确定粒子数量。具体地，对于每次迭代，KLD采样以概率(1-δ)确定样本数量，使得真实的后验分布与基于采样的近似分布之间的误差小于ε。KLD采样的抽样公式由下式给出：

式中：SX表示抽样样本；l表示样本编号；ε、δ表示误差的界；z1-δ表示上分位数为(1-δ)的标准正态分布。与传统的粒子滤波器不同的是，KLD采样将一个加权后的采样集合作为输入，因此上一时刻的样本没有被重采样。另外，将统计误差的界限限定在δ与ε之间。

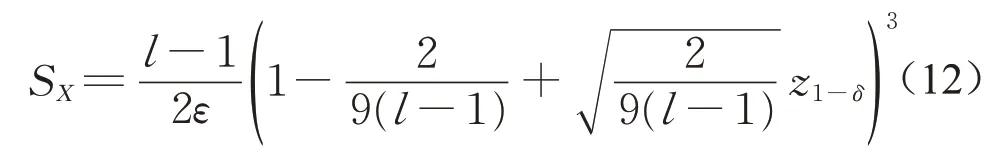
测试中ε取值为0.05，δ取值为0.2。图12为粒子滤波过程中无KLD采样与有KLD采样下粒子数变化对比。在KLD采样的作用下，粒子数随着迭代次数增加而迅速下降，之后逐渐稳定在600个粒子左右。传统粒子滤波器（无KLD采样）的粒子数不变，始终固定在设定的最大粒子数上限2 500个。由此可见，KLD采样让粒子滤波器能够自适应地调节粒子数大小，极大地提高了计算效率，降低了计算资源占用，在嵌入式系统上也可以应用。

图12 有无KLD采样粒子数变化Fig.12 Particle number change with and without KLD sampling

3 实车测试

3.1 ROS节点流图

在ROS中，数据的基本计算单元叫做节点。节点可以订阅消息，消息就是基本的数据流，经过计算之后再将消息发布出去［12］。多个节点之间可以互相通信，这也是ROS的方便之处，可以清晰地区分数据流关系。图13为ROS节点图。图13中，amcl节点是粒子滤波器的运行节点，它订阅初始位姿消息initialpose、激光雷达数据ibeolux以及tf变换消息消息。amcl_pose为最终得到的车辆定位位姿，particlecloud为粒子滤波时的粒子点云位姿数据。tf节点主要用来处理ROS中的坐标系变换，tf_bc用来播报坐标转换关系。pointcloud_to_laserscan节点用来将三维的激光雷达点云数据转化为二维平面的激光雷达点云数据，point_cloud为激光雷达原始数据，as_tx为其命名空间，ibeolux/scan为转换后的二维激光雷达点云数据。cartographer_node为前文提到的谷歌开源SLAM框架；map_server节点用于发布地图数据map；playbag节点用于发布离线测试时录制的激光雷达数据，在线测试时无需此节点，可以直接从车辆上读取数据；intialpose为车辆的初始位姿，一般在进入停车场前由GNSS+IMU的融合定位结果给出；n_rviz节点用于上位机的可视化监控。

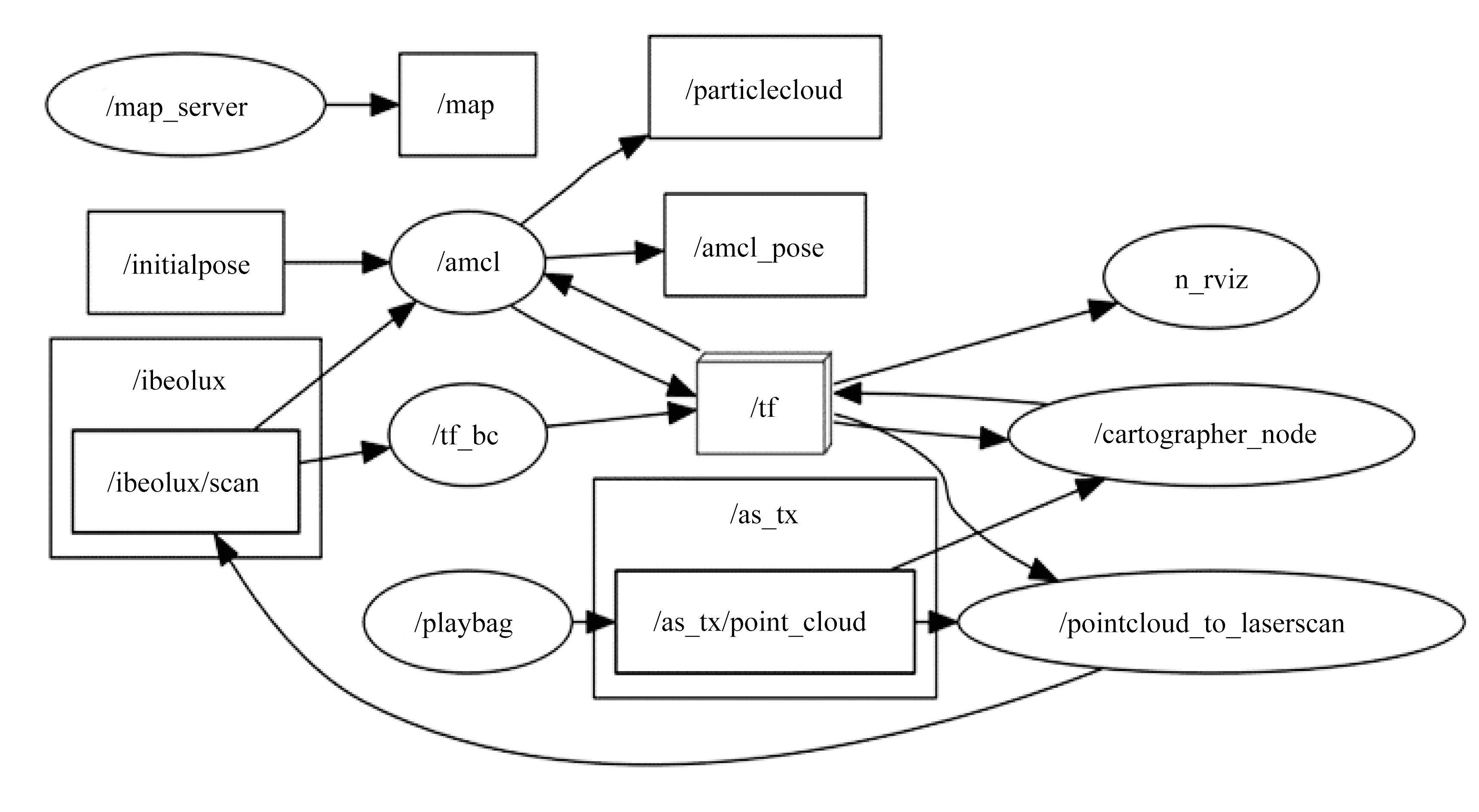
图13 ROS节点数据流Fig.13 Data flow of ROS node

3.2 定位精度分析

定位精度包括位置精度和角度精度。由于真实的车辆位姿难以获取，因此无法进行比较。粒子滤波器在提供定位的估计位姿之外，还提供了一组位姿的协方差矩阵。协方差矩阵表征了数据信息的不确定度，因此以位置信息和角度信息的不确定度作为参考信息来表征粒子滤波器的定位精度。此外，还可以通过激光雷达点云与地图的重合情况对定位精度有一个大致的判断。图14为局部的定位效果图。

图14 粒子滤波器定位匹配图Fig.14 Matching map of positioning for particle filter

图14 中黑色箭头为车辆在当前时刻的定位位姿。灰色点集为激光雷达的点云数据。黑色边框为停车场的概率占栅格地图。可以看到，点云数据与概率占栅格地图能够很好地重合，从一定程度上表明了定位的精确性。

对于定位精度的定量分析，采用协方差分析方法分析定位位置与角度的标准差，如图15、图16所示。图15中，在开始阶段粒子滤波器产生的位置不确定度标准差σp较大，这是由于已知的初始位姿并不是完全精确的，而是存在误差。粒子滤波器需要经过一定次数的迭代才能逐渐趋于真实位姿，在经过约60次迭代后，σp逐渐稳定在5.0 cm以下，平均标准差为2.3 cm，3σ为6.9 cm。根据统计学的3σ原则［13］，可以认为估计位姿与真实车辆位姿之间的误差不超过6.9 cm。图16中，车辆定位角度不确定度的平均标准差σθ约为0.01 rad，3σθ为0.03 rad，即1.8°。同样根据3σ原则，车辆定位角度的偏差不超过1.8°。

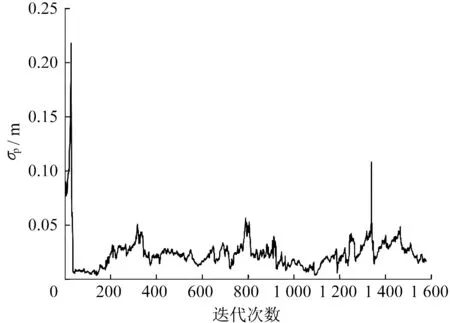
图15 定位位置标准差和迭代次数的关系Fig.15 Relationship between position standard deviation and the number of iterations

图16 定位角度标准差和迭代次数的关系Fig.16 Relationship between angle standard deviation and the number of iterations

3.3 算法实时性分析

算法的实时性直接代表着算法的效率。为保证算法的效率，首先需要设定粒子滤波器的更新策略。粒子滤波器状态的更新，并不是以时间为结算单位。如果设定时间更新，当车辆移动较慢或者车辆停止时，就会造成严重的计算资源浪费。因此，通过设置车辆的位置变化最小值，来判断是否进行粒子滤波器的迭代更新。当车辆的先验位置变化超过程序设定的最小值min_d时，便进行一次粒子滤波的重采样过程，更新车辆的位姿。

实验过程中，车辆在停车场中的平均行驶速度为1 m·s-1。当迭代最小距离min_d设置为20 cm时，粒子滤波器在理想状态下应为每秒输出5次最佳估计位姿；当最小迭代距离min_d设置为5 cm时，应为每秒输出20次最佳估计位姿。由于计算需要时间，因此实际的位姿更新频率一般都会低于理论频率。

表2展示了车辆速度v为1 m·s-1、迭代最小距离min_d分别为20、15、5 cm时理论位姿更新频率与实际位姿更新频率的关系。所有计算均基于一台6核CPU/内存16G的i7 8750H电脑，其中操作系统是Ubuntu 16.04Lts版本，ROS为Kinetic。测试车辆为一台改装过的帕萨特，搭载6个ibeo LUX 4L激光雷达。

表2 位姿更新率Tab.2 Renewal rate of pose

由表2可知，粒子滤波器定位的实际更新频率与理论更新频率相差很小，能满足车辆定位实时性的要求。实际汽车自主定位中，激光雷达的定位位姿还要与其他高频的定位位姿，如视觉里程计、轮速里程计等融合，位姿刷新频率还会得到进一步提高。

4 结语

以自动驾驶中基于激光雷达的高精度定位为目标，在GPS信号缺失的室内环境下，通过激光雷达进行车辆高精度定位。从激光雷达SLAM入手对环境进行建图，将激光雷达的点云匹配与后端图优化转化为非线性优化问题，通过高斯-牛顿迭代法进行求解。在得到精确的概率占栅格地图后，通过粒子滤波器对车辆进行定位，同时结合KLD采样等方法优化粒子滤波器中的粒子采样数量，实现了粒子采样数量的动态管理，进而缩减了计算时间。从实车测试结果可以看到，车辆定位的位置误差以及角度误差能够得到很好的控制，算法的计算复杂度较低，在一台普通配置的笔记本上也能够实现低延迟的实时定位。在保证定位精度的同时，实现了在线定位的实时性要求。该定位方法具有较强的鲁棒性，在行车过程中出现打滑等现象而导致误差的增加，粒子滤波器也能够很好地在后续的迭代过程中消除误差。

作者贡献说明：

周 苏：拟定研究方向和内容，提供指导与规划项目进度，论文修改及定稿。

李伟嘉：进行算法研究、实验测试、数据采集、论文撰写。

郭军华：提供咨询，帮助知识框架梳理，指导论文撰写，修改论文。