基于Prophet+LSTM模型的煤矿井下工作面矿压预测研究

曾庆田，吕珍珍，石永奎，田广宇，林泽东，李 超

(1.山东科技大学 电子信息工程学院，山东 青岛 266590；2.山东科技大学 计算机科学与工程学院，山东 青岛 266590； 3.山东科技大学 能源与矿业工程学院，山东 青岛 266590)

0 引 言

煤矿生产过程中矿压异常导致的生产事故，直接影响到煤矿生产的经济性、安全性、可靠性以及工作人员的安全状况等[1-3]。据统计，顶板事故占煤矿伤亡事故的40%～50%，高频率顶板事故的发生给国家带来巨大的经济损失[4-5]。随着物联网技术在煤矿开采过程中的深度应用，工作面物理环境数据得到了大量的积累，对这些数据进行深入分析与挖掘，以预测煤矿安全突发事故成为当前研究的重要方向之一[6]。国内外在矿压显现规律预测领域已经有了相当深入的研究，工作面矿压数据预测预报方法可以分为3类：①基于统计学与模糊数学等非确定性数学方法；文献[7-8]分别应用统计分析法及模糊数学理论对工作面来压进行预测和矿压显现特征分析研究。②基于矿压理论确定顶板结构，并发掘其物理力学规律的确定性方法；文献[9]采用震动波CT探测技术进行了区域应力场反演，对冲击危险区域进行了预测。③基于大量监测数据，以利用计算机分析预测为目的的系统科学或智能技术方法。文献[10]利用支持向量机对小样本预测具有良好的泛化能力和自适应多模态算法的自适应特性，提出了煤矿顶板压力实时预报的智能模式识别方法。文献[11]基于支架工作阻力大数据的矿压分析技术能够对工作面矿压规律进行精准分析。文献[12]以神东哈拉沟煤矿02212综采工作面为工程背景，进行基于PSO-BP神经网络模型的矿压预测实践研究，得出该工作面的矿压显现规律并确定影响因素。文献[13]采用灰色关联度分析法分析各影响因素与矿压的关联度，建立基于GA-BP神经网络的工作面顶板矿压预测模型。文献[14]采用深度学习方法预测了红庆河大采高工作面矿山压力，预测结果表明LSTM方法较BP神经网络预测更具准确性。虽然工作面矿压预测取得了较好成绩，但单一模型预测结果误差仍较大。总体来看，上述研究基于机器学习方法在矿压预测中取得了较好成绩，但是采用传统机器学习与深度学习方法组合和融合相邻多个支架的影响因素的研究较少。在实际应用中，时间序列预测问题通常包含线性和非线性成分，单一的预测方法不能很好地捕捉时间序列的复合特征。因此，通过深入分析时间序列数据特性，应用不同时间序列分析方法融合的组合模型进行预测分析是未来解决时间序列预测问题的趋势。目前，基于自回归移动平均模型(ARIMA)与支持向量回归模型和改进粒子群算法等方法与BP神经网络组合的预测及综合分析模型已经在采矿工程领域的预测工作中取得了较好的效果[15-16]。从上述研究中发现组合模型可以更好地捕捉时间序列数据的复杂特征。作者以鄂尔多斯盆地呼和乌素矿某工作面支架矿压时序数据为例，采用算术平均值滤波和小波去噪方法进行数据预处理，分离出所期望的信息。考虑融合相邻多个支架影响因素，利用主流的机器学习算法提出一种基于Prophet+LSTM模型预测方法对工作面矿压变化趋势进行预测，为引导煤矿安全生产部门预判顶板危机和及时制定矿井调控政策提供理论数据支撑。

1 煤矿工作面矿压预测模型

以工作面支架矿压显现规律为研究对象，结合数字信号处理技术，运用Prophet和LSTM深度学习方法分别对支架矿压时序数据进行预测，然后将2个单项模型预测结果线性加权叠加得到最终的Prophet+LSTM组合模型的预测结果。工作面矿压预测模型如图1所示，主要包括3个部分。

1)矿压时间序列数据处理：首先从矿压原始数据表中获取支架矿压原始数据；然后运用数字信号处理技术对矿压原始数据进行滤波和消噪，得到数字信号处理后的矿压序列；最后根据各支架矿压的标准偏差选择矿压波动较小的支架。

2)矿压预测单项模型：使用添加回归项方法将相邻多个支架矿压数据分别添加到Prophet模型中，然后拟合模型计算各自的RMSE值并将误差结果排序，将排序后的各支架矿压数据作为附加的回归变量依次添加到Prophet模型。使用数字信号处理后的50号支架矿压数据训练LSTM神经网络模型，数据以(X,Y)形式表示。使2层LSTM神经网络，训练时每一组数据X={x1,x2,x3,x4}为4个，x1,x2,x3,x4为时间顺序上连续4个时间段的矿压数据，Y为4个时间段后预测矿压结果。

3)基于Prophet+LSTM组合模型的矿压预测：对经过数字信号处理后的矿压时间序列数据，分别构建预测精度较高的融合相邻多个支架影响的Prophet和LSTM神经网络单项模型，通过调整Prophet和LSTM模型对应的权重线性加权叠加2个模型的预测结果，得到最终Prophet+LSTM组合模型的预测结果。

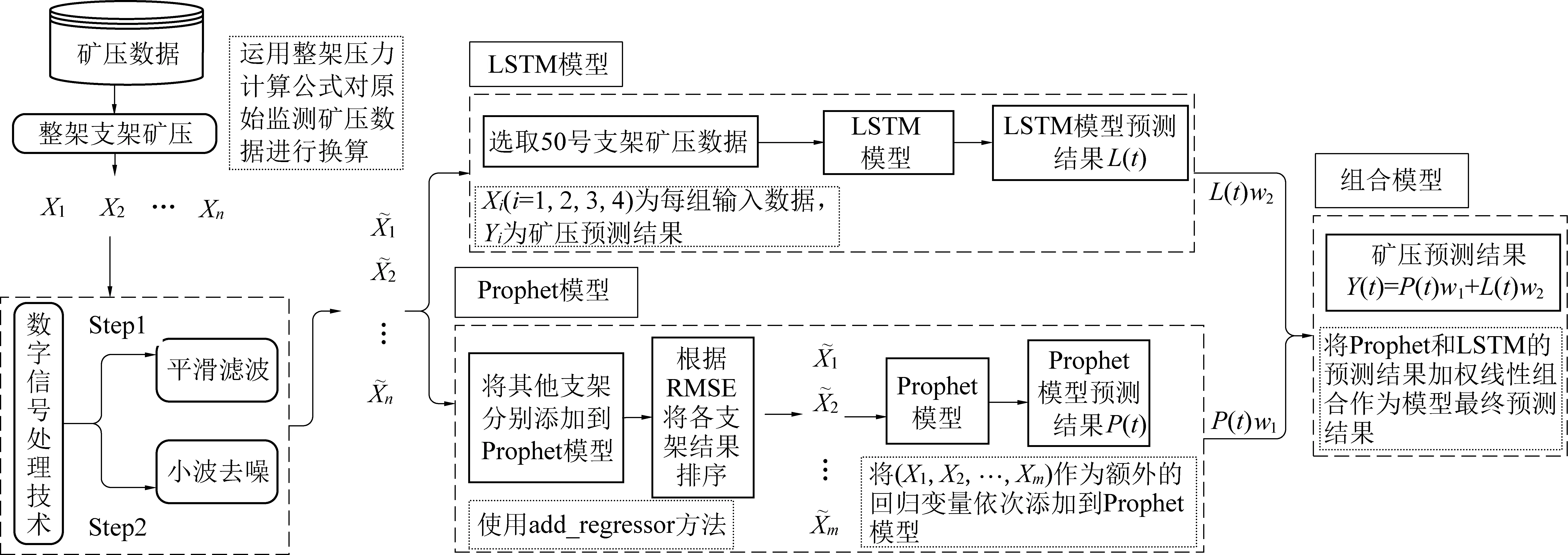
X1,X2,…,Xn—从矿压原始数据表中获取的原始矿压序列;数字信号处理后的矿压序列;相邻多个支架矿压时序数据图1 煤矿工作面矿压预测模型Fig.1 Prediction model of underground pressure in coal mining face

2 工作面矿压时间序列数据处理

由于煤矿物联网架构下的井下工作面传感器受到干扰比较多，测得的数据存在较大的噪声和随机误差，这对支架矿压预测提出了挑战。利用算术平均值滤波法来降低随机误差，采用小波去噪压缩信号，实现信号中噪声消除。

算术平均值滤波对抑制周期性干扰和随机干扰有良好效果。主要用于对压力、流量等周期脉动参数的采样值进行平滑加工，是数字滤波方法中最简单和最常用的一种，该方法是在某时刻对信号进行连续多次采样，对样本数据进行算术平均，作为该时刻的信号值。根据算术平均值滤波算法，按输入的N个工作面矿压时序数据，获取yt，使其与各矿压采样值之间的偏差的平方和最小值E,即

(1)

(2)

其中：N为样本数量；xt为时刻t的矿压采样值；yt为采样值的算术平均值。由式(2)可见，算数平均值滤波实质是将N个采样值相加求平均作为时刻t的值。

在对工作面支架矿压时序数据进行滤波后，采用小波阈值去噪方法压缩信号，提取出噪声信号中有用的支架矿压数据。小波去噪是通过短波实现噪音消除，将信号细节特征提取与低通滤波融合起来的去噪方法[17]。近年来，小波去噪理论得到了非常迅速的发展，由于其具备良好的时频特性，因而实际应用非常广泛且获得了非常好的效果。小波去噪原理如图2所示。

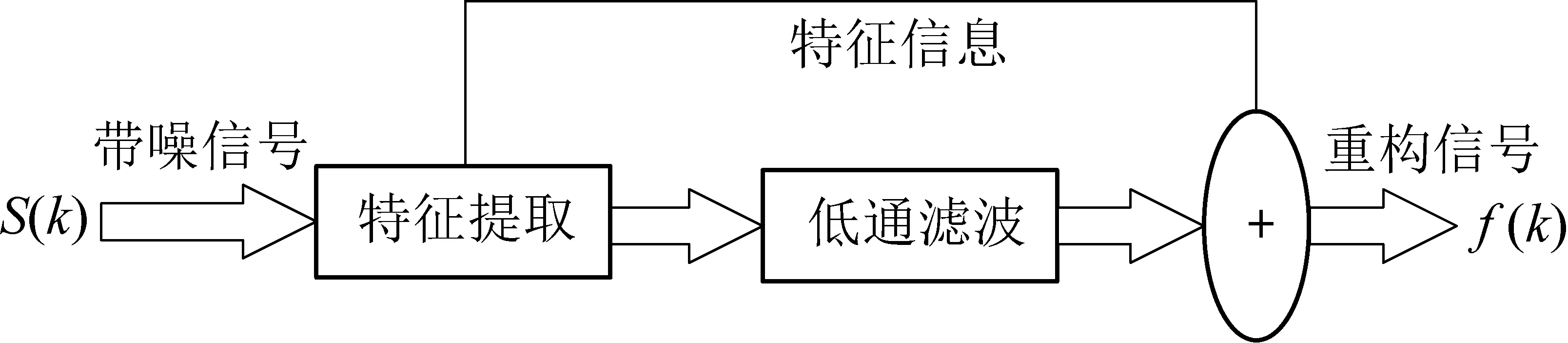
图2 小波去噪原理Fig.2 Principle of wavelet denoising

S(k)=f(k)+εe(k),k=0,1,…,n-1

(3)

其中：S(k)为含噪声信号；k为n个采样点；f(k)为有用信号；e(k)为噪声系数函数；ε为噪声系数的标准偏差。根据式(3)，提取出噪声信号中有用的支架矿压数据f(k)。

经过数字信号处理之后的矿压数据的标准偏差对比结果，如图3所示。根据误差上下波动的幅度大小选取预测模型的训练数据，50号支架矿压的标准偏差最小，因此选取50号支架数据用于预测模型训练。

考虑到数字信号处理技术对结果的重要影响，对各支架矿压序列数据在应用数字信号处理前后进行了对比分析，如图4(2019年数据)所示。选取3个支架查看数字信号处理后矿压的变化情况，可以明显看到数据趋势更加平滑，噪声减少明显。

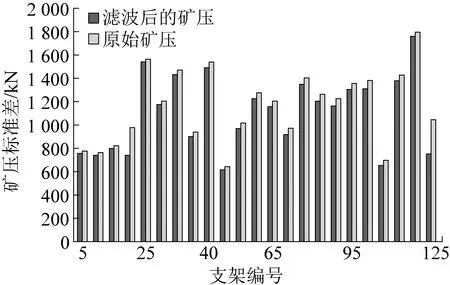
图3 数字信号处理后各支架标准差对比Fig.3 Comparison of standard deviation of each bracket after digital signal processing

3 基于Prophet+LSTM的矿压预测模型

为有效预测工作面矿压，考虑不同支架的影响因素。使用添加回归项方法将相邻多个支架的矿压时间序列数据作为额外的回归变量添加到Prophet模型，然后提出一种基于线性加权组合的Prophet+LSTM模型方法预测工作面支架矿压。

3.1 融合相邻多个支架影响因素的Prophet模型

Prophet是Facebook开源的一套时间序列预测模型工具[18]，已经在预测工作中得到了广泛应用并取得了较好效果[19-20]。Prophet在实质上采用广义加法模型来拟合和预测函数，将时间序列建模分为非线性趋势、周期性成分和节假日或特殊事件的总和，并允许融合额外的回归变量。Prophet模型还擅长处理具有异常值和趋势变化的周期数据，而工作面矿压数据具有很强的突变性。因此，将具有成分分解能力的Prophet模型用于工作面支架矿压预测。Prophet模型将时间序列按下式进行分解：

*：本项目得到漳州市林业局韩金发、何水东2位高级工程师；福建农林大学陈礼光副教授；长泰岩溪国有林场张友育高级工程师的大力支持与帮助。在此表示最诚挚的谢意!

P(t)=g(t)+s(t)+h(t)+ε(t)

(4)

其中：P(t)为Prophet模型预测结果；g(t)为趋势项；s(t)为周期项；h(t)为节日项；ε(t)为误差项。Prophet算法是通过拟合这几项，最后将其累加起来作为时间序列的预测值。其中，g(t)是整个模型的核心组件，包含不同程度的假设和调节光滑度的参数，用于拟合时间序列中的非周期性变化，从数据中选择变化点(changepoint)检测趋势走向。基本趋势项使用的是分段线性函数：

g(t)=[m+α(t)δ]t+[b+α(t)Tγ]

(5)

式中：m为增长率；α(t)为指数函数；δ为增长率的变化量；b为偏移量；γ为突变点边界。

将相邻多个支架矿压数据作为额外的回归变量使用add_regressor方法添加到趋势项g(t)中，提高Prophet模型的预测效果。首先将相邻多个支架矿压时间序列数据分别添加到Prophet模型进行预测，然后根据各自的RMSE和MAE大小排序。排序结果代表支架矿压数据对50号支架矿压数据的影响程度。因此，可以将排序后的相邻多个支架矿压数据作为额外的回归变量依次添加到Prophet模型以提高预测精度。Prophet的预测过程为：①构建数据格式，生成时间序列的时间戳和取值分别为ds和y，建立时间序列模型；②使用add_regressor方法添加额外的回归变量，拟合模型；③预测和评估模型，根据RMSE和MAE调整模型参数；④以可视化的方式反馈整个预测结果。

3.2 基于Prophet+LSTM的矿压预测组合模型

为了提高工作面矿压预测的准确度，且充分利用Prophet模型和LSTM神经网络模型的优势，提出一种基于线性加权的Prophet+LSTM组合模型用于工作面矿压预测。

首先对矿压时间序列数据构建预测精度较高的Prophet和LSTM神经网络单项模型，设定Prophet模型在t时刻的预测值为P(t)，LSTM神经网络模型的预测值为L(t)，t=1,2,...,n，并设定2个模型的权重系数分别为w1和w2。则，Prophet+LSTM线性加权叠加模型预测结果公式如下。

(6)

其中：设定N为11，由于w1i+w2i=1，设定权重系数w1i为[1，0]递减的11个数值，则w2i为[0，1]递增的11数值。首先将这11组权重系数w1i和w2i别与Prophet和LSTM神经网络模型在t时刻下的矿压预测结果相乘，然后将相同时刻两个模型带有权重系数的预测结果相加，最终得到组合模型的预测结果。最优权重系数获取方法如图5所示。

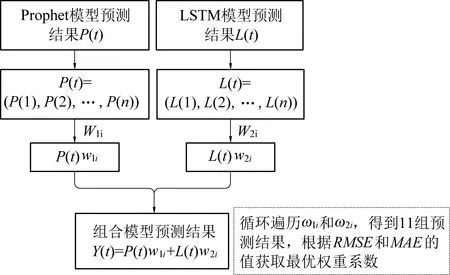
图5 获取最优权重系数Fig.5 Get optimal weight coefficient

4 试验结果分析

为有效评估上述方法预测工作面支架矿压的实际效果，首先构建预测精度较高的Prophet和LSTM神经网络单项模型，然后基于线性加权的Prophet+LSTM组合模型建模。最后，与2种经典的时间序列预测模型预测效果进行比较，验证所提出的方法具有更好的准确性和预测能力。

4.1 数据集介绍

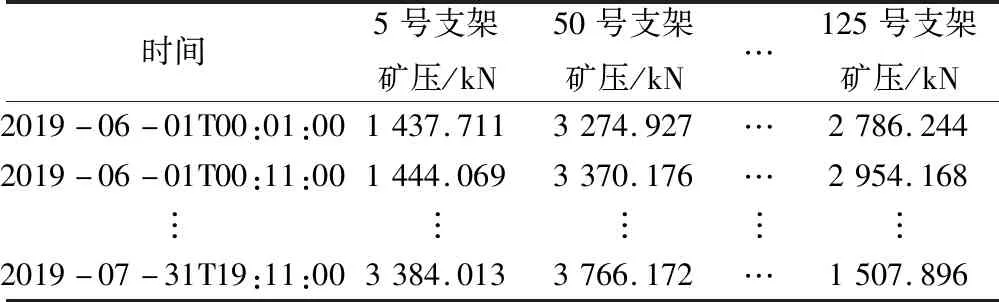
表1 原始数据集示例Table 1 Example of original data set

4.2 评估指标

选用均方根误差(RMSE)、平均绝对误差(MAE)作为评估各组权重系数对应的Prophet+LSTM模型效果的标准，计算公式如下

(7)

(8)

4.3 融合滤波技术和相邻多个支架的影响因素的预测结果分析

为了有效地预测工作面矿压，考虑到不同滤波情况对预测模型的影响因素，设计3种不同的数据处理方法(表2)，通过试验对比3种数据处理方法对预测模型预测准确性的影响。方法1，用于预测的50号支架和其他相邻多个支架矿压数据均使用原始矿压数据；方法2，仅将用于预测的50号支架矿压数据进行数字信号处理方法处理，而其他相邻多个支架矿压数据使用原始矿压数据；方法3，用于预测的50号支架和其他相邻多个支架矿压数据都进行数字信号处理方法处理。

表2 3种数据处理方法Table 2 Three data processing methods

使用RMSE和MAE对各个方法进行比较，试验结果如图6所示。

图6 随着滤波情况变化的预测结果对比Fig.6 Comparison of prediction results with changes in filtering conditions

由图6知，方法3预测结果的RMSE和MAE最小。试验结果表明，经过数字信号处理之后的矿压时间序列数据在预测模型中具有更高的准确性。

将融合额外回归变量的Prophet模型预测结果根据式(7)和式(8)与真实矿压数据进行比较，然后根据加入不同支架数后的误差值，验证所提出的融合相邻多个支架影响的Prophet模型的预测性能，结果如图7所示。

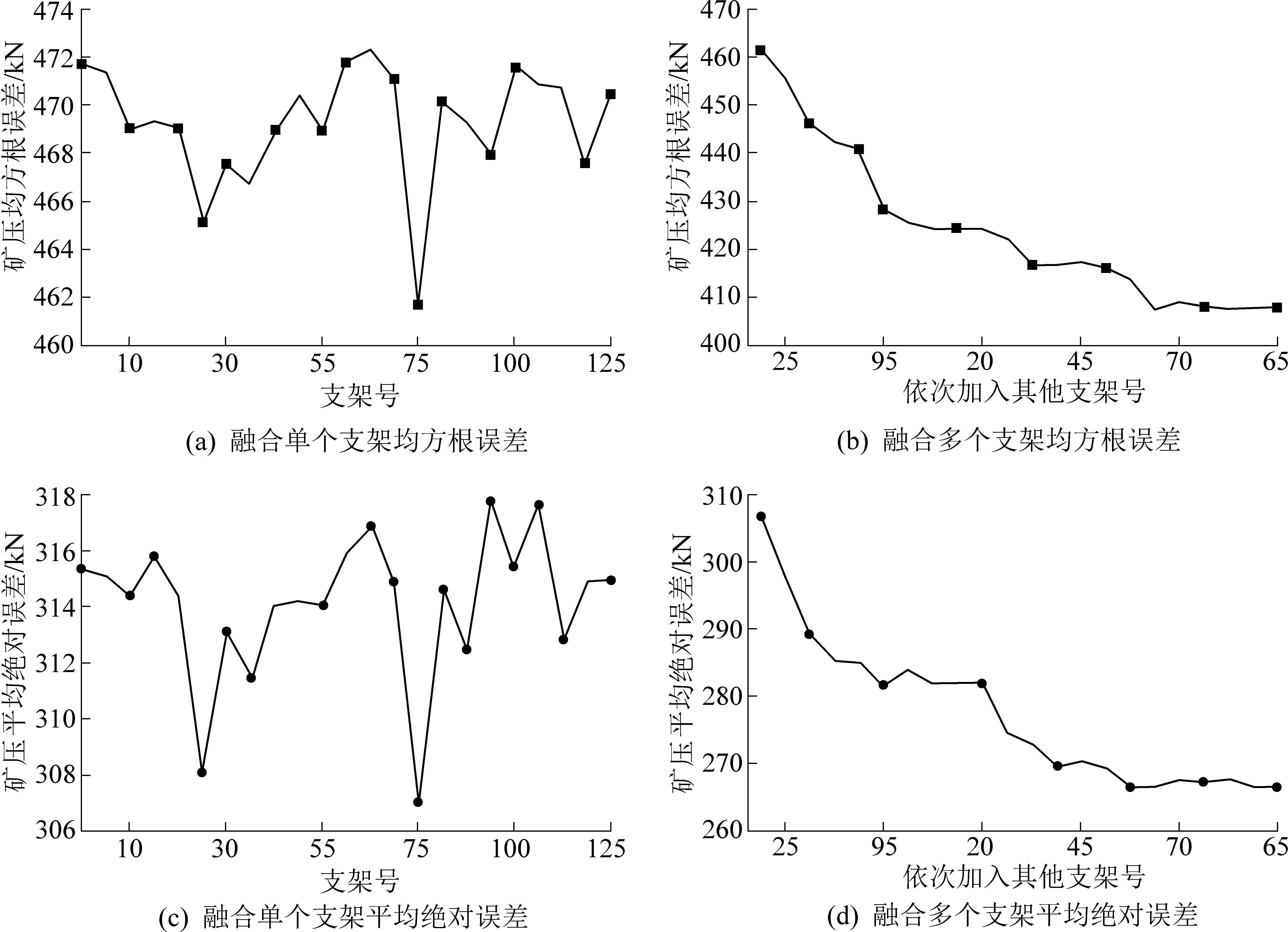
图7 融合不同支架数量的误差对比Fig.7 Error comparison of fusion of different stent numbers

图7a是将单个支架作为额外的回归变量添加到Prophet模型进行预测的RMSE和MAE，可以明显看到25和75号支架对50号支架的影响力度较大；图7b是根据图7a中的结果排序后依次融合到Prophet模型的结果，随着支架数量的增加，RMSE和MAE逐渐减少，当融合到105号支架时RMSE减少了64.307 kN(13.6%)，MAE减少了48.766 kN(15.5%)，之后误差基本不再变化。结果表明：融合相邻多个支架矿压数据作为附加的回归变量添加到Prophet模型的线性部分，可以提高Prophet模型的预测精度。

表3为不同训练集占比的试验结果，根据表3，将融合相邻多个支架的矿压时间序列数据按9∶1划分为训练集和测试集，使用训练集训练模型，测试集进行测试。图8(2019年数据)是Prophet模型的最终拟合效果及预测结果，由图8可知，只有少量数据不在置信区间内，说明该区间内的支架矿压变化趋势与历史数据变化趋势的相关性较大。

4.4 不同模型预测性能试验对比

表4是融合相邻多个支架影响的Prophet+LSTM组合模型不同权重系数的预测结果。在表4中，当权重系数w1=0.2，w2=0.8时，预测结果MAE最小；当权重系数w1=0.3，w2=0.7时，预测结果RMSE最小；当权重系数w1=0.2，w2=0.8时，RMSE与MAE的和最小。结果显示，相对于Prophet和LSTM模型，Prophet+LSTM模型的预测效果明显提高，其预测效果总体上优于其单项预测模型。

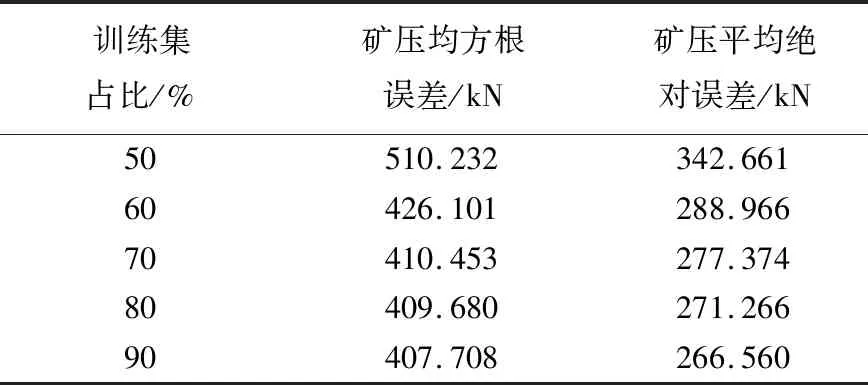
表3 不同训练集占比的试验结果Table 3 Experimental results of different training set proportions

—实际值；—预测值；—置信区间； 不存在黑色圆点的数据区间表示对矿压趋势的预测区间图8 Prophet模型预测结果Fig.8 Prophet model prediction results

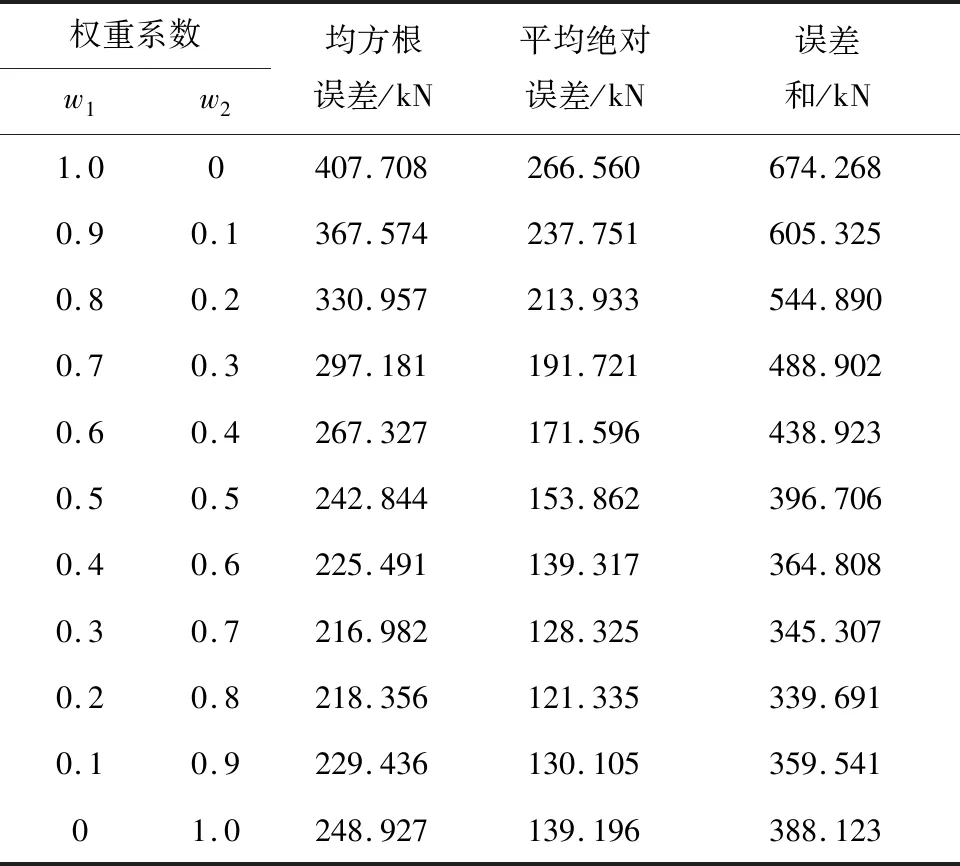
表4 不同权重对应组合模型的RMSE和MAETable 4 RMSE and MAE values of combined model corresponding to different weights

为进一步验证Prophet+LSTM组合模型的应用性能，选取ARIMA模型、BP神经网络模型、Prophet模型、LSTM、Prophet+LSTM组合模型作为对比模型。对工作面支架矿压数据进行建模预测，各模型评估结果见表5。表5得Prophet+LSTM组合预测模型、Prophet和LSTM单项模型的预测性能明显优于ARIMA和BP神经网络经典时间序列模型。且Prophet+LSTM模型预测结果误差值最小，预测效果最佳，可作为一种有效的工作面矿压预测模型。

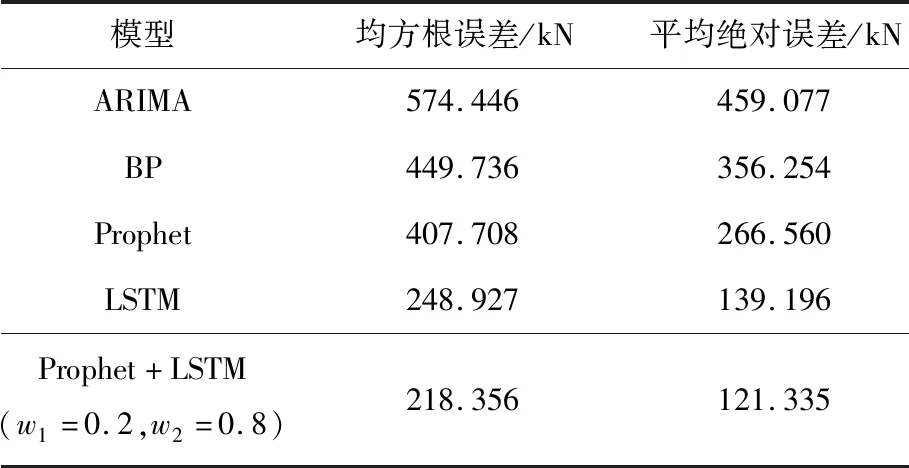
表5 不同模型的性能对比Table 5 Performance comparison of different models

5 结 论

1)将算术平均值滤波和小波去噪方法运用到矿压预测模型中，设计3种不同的数据处理方法处理支架矿压数据。分析表明传感器测得的数据经过数字信号处理可以减少噪声和随机误差，提高了矿压预测模型精度。

2)在Prophet模型中添加相邻多个支架矿压数据可以提高其预测精度，对比未考虑融合相邻多个支架影响的预测结果，RMSE和MAE误差分别减少约14%和15%。将深度学习方法引入到矿压预测中，解决了传统浅层神经网络加深遇到的问题，对比BP神经网络模型预测结果，LSTM模型RMSE和MAE误差值分别减少约45%和61%，表明LSTM在捕捉时序特性上有更强的能力。

3)将Prophet+LSTM组合模型的预测方法应用到工作面支架矿压预测中，解决了单项模型预测方法不能很好地捕捉时间序列的复合特征问题，提高了支架矿压预测模型的精度。对比LSTM模型预测结果，Prophet+LSTM模型RMSE和MAE误差分别减少约12%和13%，结果表明Prophet+LSTM组合模型的预测效果明显提高，预测效果总体上优于单项模型。