KNN优化的密度峰值聚类算法*
黄学雨,程世超
(江西理工大学,江西 赣州 341000)
0 引 言
聚类算法是一种常用的在数据集中寻找簇结构的方法,其目的是使得数据集中同一个簇内的数据具有最大相似性,不同簇之间具有最大差异性。在不同的科学领域具有广泛的应用,尤其在无人监督的学习场景中有着重要的应用[1-4]。根据聚类算法中样本空间中数据点之间目标函数定义方法不同以及各聚类簇内和簇间的数据对象间的关系,聚类算法一般分为基于划分的方法、基于层次的方法、基于网格的方法、基于密度的方法和基于模型的方法,其中基于划分的方法被广泛研究与应用[5]。
基于划分方法假设数据集可以用有限的聚类原型来表示,这些原型具有各自的目标函数,因此定义一个点和一个聚类原型之间的差异(或距离)是划分方法的关键。K-means算法是最流行的一种划分方法[6]。由于K-means算法的初始聚类中心设置对聚类效果影响较大,因此有效提高初始聚类中心的设置一直是K-means算法的研究热点。Pelleg和Moore[7]提出了X-means算法,通过在K-means的每次迭代中对聚类中心进行局部决策,并对其进行自我分裂,从而得到更好的聚类结果;Bezdek等[8]结合数学中的隶属度函数表示数据点属于类簇的概率值,提出了FCM算法,但该算法对初始聚类中心c和柔性参数m这两个参数较敏感;Khan等[9]提出以数据点间的距离均值、标准差等统计信息作为数据点的密度信息,即类中心自动初始化算法(Cluster Center Initialization Algorithm,CCIA)算法;Redmond等[10]通过构建k-d树计算出数据集中数据对象的密度分布情况,并利用数据点的密度信息获取数据集的初始聚类中心,提高聚类精准性;文献[11]利用萤火虫优化算法的特点优化初始聚类中心的选择;文献[12]引入改进的森林优化算法提高原始K-means算法的收敛速度和收敛精度;文献[13]提出基于距离和权重来计算样本点的密度,并以密度最大的数据点作为初始聚类中心点;文献[14]引入二次幂思想预处理数据集,然后计算样本点的密度来初始化聚类中心点。尽管目前有大量各种改进的K-means聚类算法,在一定程度上提高了算法的聚类效果和收敛速度,但参数设置过多并且参数的选择对算法的聚类效果影响太大。本文提出一种基于K-最近邻(K-Nearest Neighbor,KNN)优化的密度峰值的K-means算法,使用KNN的思想优化局部密度,并以样本数据点平均距离代替原始密度峰值算法的截断距离,再利用平均局部密度检测和去除离群点,最后结合提出的自适应合并策略合并相似类簇,从而获取初始聚类中心,提高K-means算法的聚类性。
1 密度峰值聚类算法介绍
密度峰值聚类(Density Peaks Clustering,DPC)算法的典型代表是快速搜索和查找样本密度峰值的聚类算法。DPC[15]算法的基本思想:聚类簇中心点的局部密度大于属于该聚类簇所有样本点的局部密度,并且与其他聚类簇中心点距离较远。根据DPC算法这两个特点建立决策图,样本数据点的局部密度 ρi为:

δi表示数据样本点i与比它局部密度更高的点之间的欧式距离,表示为:
如果i=j,则δi定义为:
DPC算法通过ρi和δi构建决策图来选取聚类中心,再根据聚类中心把剩余样本数据点归类于离其最近的聚类簇。
根据式(1)可知,截断距离dc选取值的不同对DPC聚类算法影响很大,并且原始的DPC算法对于小型数据集的聚类效果并不好。因此,有文献提出当数据规模较小时,使用高斯核定义样本数据点的局部密度,公式如下[16]:
在实际应用中是没有客观方式来度量一个数据集的大小,并且在小数据集上使用式(4)来定义样本数据点的局部密度,截断距离dc的大小对于聚类效果影响还是很大,一旦一个数据样本点聚类错误将会产生连锁反应,将导致整个数据样本点聚类不佳的情况[17]。为了解决以上原始DPC聚类算法的问题,本文提出基于KNN优化密度峰值算法,使用KNN的思想和一种新的密度定义函数代替截断距离dc来确定数据样本点的局部密度,并提出一种自适应合并策略来合并相邻聚类簇。
2 改进的密度峰值聚类KDPC算法
2.1 改进的KDPC算法基本思想
由于DPC聚类算法易受截断距离dc的影响和对不同大小数据集的要使用不同的局部密度函数,本文通过使用高斯核函数,提出基于KNN优化的DPC算法。该算法使用KNN获取K个数据点的最近邻信息,再利用样本数据点的最近邻信息定义一种新的局部密度函数。该密度函数可以适应不同大小数据集并且不需要人工设定截断距离dc,并将dc定义为一个普适性的公式[18]。改进的DPC算法减少了人为干预,并将在各种数据集得到更好的聚类效果,其改进的样本数据点的局部密度度量公式如下:

为了提高聚类效果的精确性,减少异常点对聚类效果的影响,在使用改进的DPC算法对样本数据集获取初始聚类中心点之前,需要检测和去除样本数据集中的离群点[19]。本文提出以下定义:如果样本数据点的局部密度小于样本数据集的平均局部密度,则标记该样本数据点为离群点,即样本噪声点。样本噪声点的识别函数如下:
2.2 自适应合并策略优化KDPC
为了提高KDPC算法对样本数据集的聚类性能,本文提出一种对于聚类簇的自适应合并策略,该策略主要是通过以下定义把聚类簇进行合并,从而获得更好的聚类中心。
定义1簇心均值。一个聚类簇中所有数据点到簇心距离的平均值,表示为:
式中:ηk表示第k个聚类簇中所有数据点到簇心的平均距离;|Ck|表示第k个聚类簇中数据点的个数;Ck-c表示第k个聚类簇的中心点。
定义2簇内边界点。若两个聚类簇之间,存在一对数据点的距离小于两个聚类簇中任意一个聚类簇的簇心均值,则把这两个数据点成对保存到一个集合中。
式中:Pkm表示聚类簇k和m的所有的边界点。
定义3边界点的密度。根据定义1和2可重新定义聚类簇k边界点的局部密度ρkP。
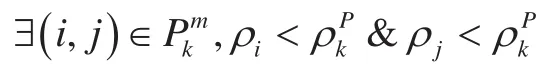
根据以上两个条件可知,两个聚类簇之间只要满足它的簇内边界点不为空,且存在边界点的密度大于两个聚类簇的局部密度。那么,这两个聚类簇是密度直接可达的。
定义5密度可达。如果存在类簇k和类簇m直接密度可达,类簇m和类簇l也直接密度可达。那么,类簇k和类簇l是密度可达的。
改进的DPC算法在去除噪声点基础上,可以获取较好的初始聚类簇,但可能会存在一些很相似的聚类簇。通过以上定义,可以很好地识别出密度可达的聚类簇,并将它们进行合并,合并之后的聚类簇不会太大改变初始的聚类中心,将大大提高算法对聚类中心获取的准确性。
3 基于KDPC优化的K-means聚类算法
3.1 K-means基本思想
K-means算法是一种常见的聚类算法,在对小数据集聚类时有着良好的聚类效果。K-means算法的核心是将n个样本的数据集合划分为K个类簇,使得每个簇内的样本相似度高,簇间的样本相似度低,设X={x1,…,xn}是d维欧氏空间中的一个数据集Rd,设A={a1,…,ac}是c个聚类簇的中心。用dist(x,ai)表示x∈ai与该聚类簇中心ai之差,其计算公式如下:
K-means算法使用误差平方和(Sum of Squares due to Error,SSE)作为度量聚类质量的目标函数,其内涵是各聚类簇内样本数据点之间的紧密程度,SSE越小,簇内样本数据点相似性越高,反之越小。SSE的计算公式如下:
式中:x表示样本数据点;p为数据对象的特征属性;dist(x,ai)表示在聚类簇中的样本数据点与聚类中心ai的欧式距离;ni表示属于第i聚类簇的样本数据点的个数。
3.2 KDPC-K算法思想
KDPC-K算法思想主要分为以下两个部分。
(1)改进的密度峰值算法部分:运用改进的KDPC算法思想计算出所有样本点的局部密度ρi和δi,根据ρi和δi的值构建决策图,假设样本数据集划分为K类,则选择前K个ρi和δi的值较大的样本数据点作为聚类中心点。
(2)K-means算法部分:使用第一部分得到的聚类中心点作为K-means算法的初始聚类中心点,开始循环迭代,直至满足迭代次数t或更新前后的目标函数值的误差很小则停止迭代,从而获得更好的聚类效果。
3.2.1 KDPC部分算法
输入:样本数据集X,类别数K。
输出:初始聚类中心集ci(0)。
(1)对样本数据集进行归一化处理;
(2)计算所有样本数据点的欧式距离,并根据式(5)计算样本点的局部密度ρi;
(3)根据式(6)和式(7)标记和去除噪声点;
(4)根据式(8)、式(9)分别计算所有聚类簇的ηk、Pkm和ρkP,并根据定义4和5合并相似的类簇;
(5)根据式(2)计算类簇的δi;
(6)根据ρi和δi的值构建决策图,并选取前c个样本点作为初始的聚类中心点集ci(0)。
3.2.2 K-means部分算法
输入:样本数据集X,初始聚类中心点集ci(0)。
输出:聚类中心点集ci。
步骤1:初始化迭代次数t,令t=0;
步骤2:根据初始聚类中心点集ci(0),由式(10)和式(11)计算目标函数SSE(t)的值;
步骤4:再由式(10)和式(11)计算目标函数SSE(t+1)的值判断SSE(t+1)-SSE(t)>ε是否成立,若成立则转到步骤3,否则迭代中止;
步骤5:算法对数据集完成上述步骤之后,经过多次迭代得到最终的聚类中心点集ci。
3.3 KDPC-K算法复杂度分析
KDPC-K算法的主要由KDPC算法和K-means算法组成,在KDPC算法对样本数据集处理过程中,假设要处理的样本数据集的大小为n,要存储每个样本数据点的k近邻信息则需要o(nk)空间;还需要存储每个样本点的δ和ρ值则需要o(2n)空间;最后,KDPC算法需要存储每个类簇的边界点对,最不理想的情况需要o(n2)空间。获得初始聚类中心点集之后,K-means聚类算法使用快速排序存储数据点的欧式距离需要o(n1gn),因此,KDPC-K算法总的空间复杂度为o(n2)。KDPC-K算法的时间复杂度由以下几点决定:
(1)计算数据点之间的距离的时间复杂度o(n2),但可以用快速排序把时间复杂度降至o(n1gn);
(2)每个类簇的边界点的数量理论上可以达到n,计算边界点密度的时间复杂度为o(n2)。因此,KDPC-K算法总的时间复杂度为o(n2)。
4 实验结果与分析
4.1 聚类性能评价指标
为验证算法在样本数据集上聚类结果的性能,本文采用Precision和Recall加权调和平均F、RI指数、相似系数系数J、精准率P和召回率R来评价算法的聚类效果。这5种评价指标都是其值越大表示算法的聚类效果越好,取值范围都在[0,1]之间,这5种评价指标的计算公式为:
式中:β是一个参数,P、R、J的计算公式如下:
式中:|F|表示算法的聚类结果中分类的数量;|T|表示样本数据集原始的分类数量;|T∩F|表示算法的聚类结果中正确分类的数量;|T∪F|表示聚类结果的样本分布和原始数据集样本分布的数量。
RI指数计算公式为:
式中:TP+TN表示本属于同一个类簇的样本点被分到一起的对数和本不属于同一类簇的样本点被分到不同类簇的对数之和;FP+FN表示分类错误的样本点的对数。
4.2 KDPC-K算法的可视化聚类效果及分析
为了检验KDPC-K算法的聚类效果,实验通过在4种数据集上对比KDPC-K、文献[12]、文献[13]和文献[14]这4种算法的聚类效果,在聚类效果图中,不同的颜色代表不同的类簇,实验过程中文献[13]和文献[14]算法的参数设置为最佳,实验数据集的分布如图1所示。
其中,样本数据集Data1共有567个数据点,分成两个类簇;样本数据集Data2共有3 603个数据点,分成3个类簇;样本数据集Data3共有785个数据点,分为7个类簇;样本数据集Data4共有3 100个数据点,分为31个类簇,数据集的具体信息如表1所示。

表1 4种数据集信息
4种算法在样本数据集Data1上实验的聚类效果如图2所示,可以得出KDPC-K、文献[12]和文献[14]算法都能够准确识别样本数据点并得到准确的聚类结果。然而,文献[13]算法没有得到准确的聚类个数,将一个类簇错误地分为两个类簇。
4种算法在样本数据集Data2上实验的聚类结果如图3所示,可以得出KDPC-K、文献[14]和文献[13]算法都能够获得正确的聚类结果,而文献[12]算法没有将样本数据点归类正确。虽然文献[13]和文献[14]的算法获得了准确的聚类结果,但需要更多的参数设置。
4种算法在样本数据集Data3上实验的聚类结果如图4所示。从图4中可以得出文献[12]和文献[13]算法聚类效果最差,把一个类簇分为两个并且一些其他的类簇数据点归类错误,KDPC-K和文献[14]算法取得正确的聚类结果。虽然文献[14]和KDPC-K算法都取得了正确的聚类数,但文献[14]算法对参数的依赖性更大,并且KDPC-K算法在此数据集上的聚类效果表现更佳。
4种算法在样本数据集Data4上实验的聚类结果如图5所示。从图5中可以得出,4种算法在样本数据集上都取得了正确的聚类簇数。但文献[13]、文献[14]算法需要人工选择较多参数,一旦参数选择不好,对算法的聚类效果影响较大,并且KDPC-K算法的聚类效果比文献[12]算法更好。因此,KDPC-K算法聚类性能更佳。
4.3 KDPC-K算法的性能指标分析
为了检验KDPC-K算法的聚类性能,实验通过在UCI数据集上对比KDPC-K、文献 [12]、文献[13]和文献[14]这4种算法的性能指标和运行时间,UCI数据集的具体信息如表2所示。

表2 UCI数据集信息
在实验中,每种算法都在各数据集上运行40次,以3种性能评价指标的均值和平均运行时间作为4种算法的聚类性能,4种算法在UCI数据集上的性能指标如表3所示。

表3 4种算法在UCI数据上的性能指标及运行时间
从表3中可以得出,在Iris数据集上,KDPC-K算法比其他3种算法的性能指标更佳,在F指标上KDPC-K算法比文献[12]、文献[13]和文献[14]分别高出0.038 7、0.037 5和0.051 9,在J指标上KDPC-K算法比文献[12]、文献[13]和文献[14]分别高出0.104 0、0.060 3和0.055 9,在RI指标上,KDPC-K算法比文献[12]、文献[13]和文献[14]分别高出0.043 3、0.037 9和0.034 6,并且KDPC-K算法的平均运行时间最少,文献[13]和文献[12]次之,文献[14]最长;在Segment数据集上,4种算法的性能指标比在Iris数据集更低并且平均运行时间更长,这是由于Segment数据集更大,特征维数和类别数更多并且数据及分布形态更复杂,KDPC-K算法的性能指标依旧比其他3种算法更佳,KDPC-K算法的3种性能指标比另外3种算法高出0.1~0.2,KDPC-K算法的平均运行时间最少,文献[14]的算法平均运行时间最长;4种算法都在Wine数据集上表现得比在其他数据集更好,Wine数据集数量小、特征维数和类别数少,数据集分别形态不复杂,KDPC-K算法的性能指标仍然比其他3种算法高出0.1~0.3,文献[13]和KDPC-K算法的平均运行时间相差不大,文献[12]和文献[14]算法的平均运行时间较长;由于Pageblocks数据集的样本数量是最多的,所以4种算法的平均运行时间也是最长的,在4种算法中KDPC-K算法的平均运行时间最短,文献[14]算法的平均运行时间最长。因为文献[12]只是利用改进的森林算法提高K-means算法的寻优能力来避免算法陷入局部最优,对原始K-means算法对初始聚类中心的敏感并没有改进。文献[13]和文献[14]虽然对K-means算法的初始聚类中心进行了改进,但该算法其中的参数对聚类性能影响较大,并且对数据集的倾斜问题比较敏感,总之KDPC-K算法的聚类性能指标和平均运行时间都比其他3种算法表现更佳。
4.4 KDPC-K算法的抗噪性和鲁棒性分析
为验证KDPC-K算法的抗噪性和鲁棒性,使用KDPC-K、文献[12]、文献[13]、文献[14]算法在同一人工合成数据集上进行实验,人工合成数据集的具体信息如表4所示。

表4 含有噪声的合成数据集信息
实验过程中每种算法都在数据集上运行40次,取4种算法的评价指标均值作为聚类性能值,4种算法的聚类结果指标如表5所示。
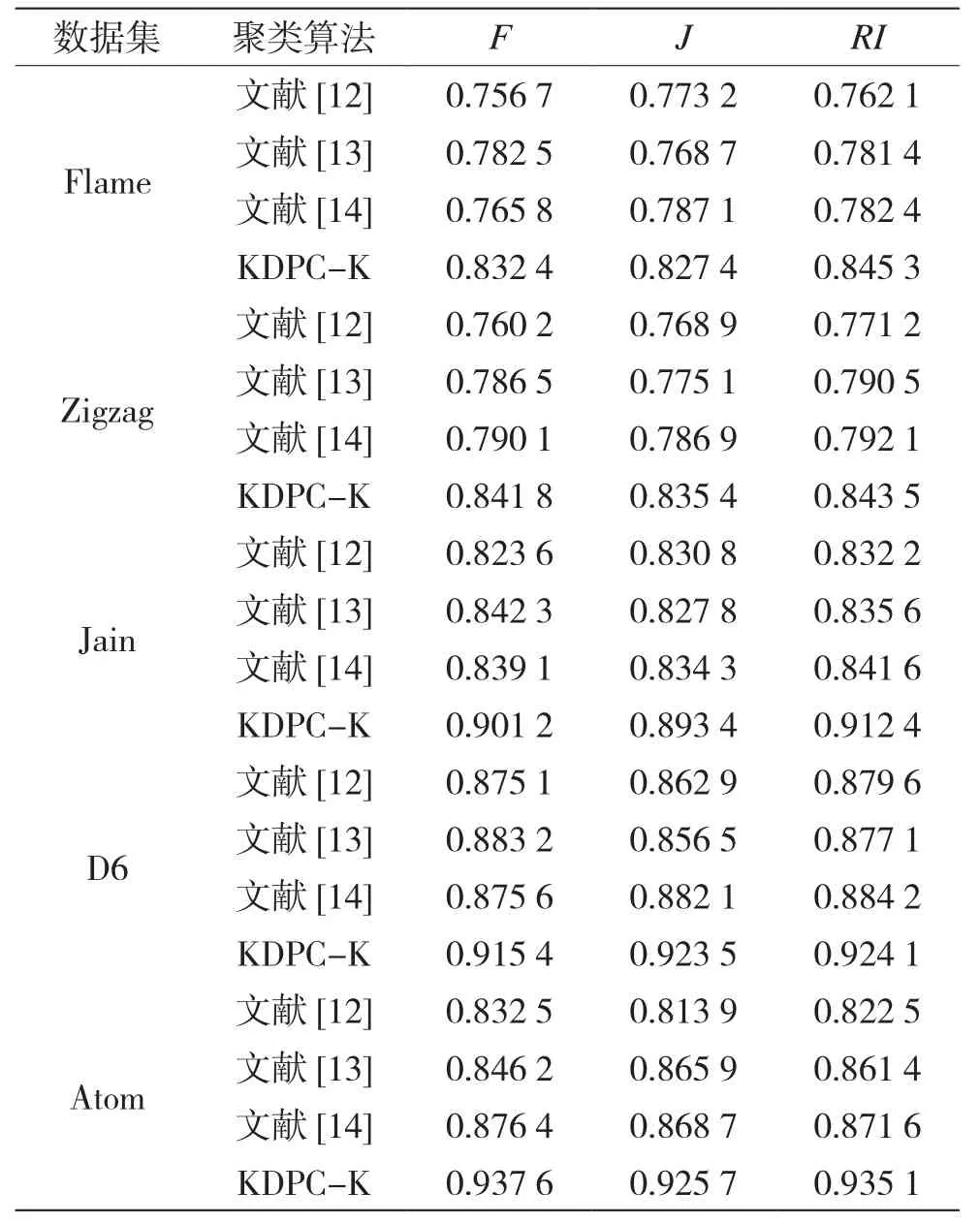
表5 4种算法在含噪声的数据集上的性能指标
表5显示了KDPC-K、文献[12]、文献[13]和文献[14]这4种聚类算法在含噪声的合成数据集上的聚类性能。在Flame数据集上,文献[12]和文献[14]算法的3种聚类性能指标相差不大,文献[13]算法的性能指标比以上两种算法好,KDPC-K算法的聚类性能指标最佳;在Zigzag数据集上,文献[12]算法聚类性能指标最差,文献[13]和文献[14]算法在RI指标表现相差无几,但在其他两种性能指标上文献[14]算法表现得更好一些,KDPC-K算法在各项性能指标上都比其他3种算法更好;在Jain数据集上,文献[12]、文献[13]和文献[14]这3种算法表现一般,与KDPC-K算法在各种性能指标上相差较多;在D6数据上,文献[13]算法除了在Jaccard指标上与文献[12]和文献[14]表现不佳,在其他两种性能指标上3种算法表现差不多,KDPC-K算法的3种性能指标都较大;在Atom数据集上,文献[12]和文献[13]算法的性能指标都比其他两种算法低,KDPC-K算法比文献[14]算法表现更佳。因为文献[12]只是利用改进的森林算法提高K-means算法的寻优能力来避免算法陷入局部最优,对原始K-means算法对初始聚类中心的敏感并没有改进。文献[13]虽然对K-means算法的初始聚类中心进行了改进,但该算法其中的一个参数对聚类性能影响较大,并且对数据集的倾斜和噪声问题比较敏感,文献[14]算法也没有解决数据集中噪声的问题。总之,在5种含有噪声点的合成数据集上,KDPC-K算法的3种性能指标都比其他3种算法表现更佳。
5 结 语
本文针对K-means算法对初始聚类中心敏感和易受噪声点的影响,提出一种基于KNN优化的DPC的K-means算法(KDPC-K)。该算法利用KNN思想和改进的密度函数优化样本数据点的局部密度,并以平均密度作为阈值去除离群点,再结合自适应策略合并相似的类簇来提高聚类中心点的精确性,最后,通过取得的类簇中心点集作为K-means算法的初始聚类中心。为了验证KDPC-K算法的聚类效果,本文先通过在UCI数据集上以图示的方式验证分析KDPC-K聚类的有效性,然后在含有噪声的合成数据集和UCI数据集上比较KDPC-K和文献[12-14]这4种算法的聚类性能。实验证明:KDPC-K算法能够有效提高传统K-means算法的聚类性能,并且比其他改进的算法聚类效果更佳。

