跳频信号参数估计的核函数优化及仿真*
孙文璐
(陆军工程大学,江苏 南京 210001)
0 引 言
跳频通信技术是军事通信系统中一种常用的通信技术,也是我军开展军事侦察任务时必须考虑的一类通信手段。本文主要针对跳频信号的频点、跳频周期和跳频时刻等参数的估计方法进行研究,重点改进了在模糊函数域中,滤除交叉项所使用的核函数,旨在进一步提升低信噪比环境下的跳频信号参数估计的成功率,降低各参数的估计误差,为后续的通信干扰等工作打好基础。
1 问题描述
跳频信号是一种常见的非平稳信号,它的载波频率一般按照收发双方事先约定的规律随时间周期性跳变。单个跳频信号在独立的跳频周期内具有载波频率恒常的特点,所有可能的载波频率(也称频点)的集合就是这个跳频信号的频率集合。跳频信号的时域波形函数[1]为:
式中:s0(t)表示跳频信号每一跳的信号分量;T表示整个观测时长;TH表示一个跳频周期;αTH表示频率跳变时刻;fk表示第k跳的载波频率。
跳频信号的参数估计,通常是指估计跳频信号的频点、跳频周期和频率跳变时刻等参数。本文针对这3个参数的估计算法进行了研究。
2 基于模糊函数的核函数设计
分析一个跳频信号的时频域特征,通常将该信号的解析信号转换到时频域中,再对其时频分布进行分析。根据解析信号的定义,跳频信号s(t)的解析信号x(t)可写作:
解析信号x(t)的维格纳-威尔分布(Wigner-Ville Distributions,WVD)一般定义为[2]:
式中:x*(t)表示x(t)的复共轭函数。
跳频信号的WVD是在时频域对其解析信号的双线性变换作关于τ的快速傅里叶变换(F ast Fourier Transform,FFT),表示的是原有信号在时频域的能量分布情况,如果对解析信号x(t)的双线性变换作关于t的FFT,即
则可获得信号在时偏和频偏平面(又称相关域)的能量分布情况,该函数被称为信号的模糊函数[3]。根据定义可知,WVD与模糊函数可通过二维FFT进行转化。
维格纳分布的优势在于能够比其他时频分析方法更准确地保留跳频周期和频点参数,但其也具有明显的缺陷,即存在大量的交叉项干扰。为了克服WVD中的交叉项干扰,通常需要在模糊函数域内设计一种核函数,对模糊函数中的交叉项进行滤除[4]。由于跳频信号的载波频率具有短时恒常的特点,其模糊函数能量通常呈现出自项围绕原点集中分布,而交叉项远离原点分散且关于原点中心分布的特点[5]。利用能量分布的这一特性,选择合适的核函数即可有效滤除大部分的交叉项分量。
对信号的模糊函数作加权的二维FFT,即
式(6)表示信号在时频域的能量分布函数,其中的加权函数被称为核函数。核函数的设计应当做到在尽量保留自项的同时,滤除最多的交叉项。因此当核函数趋近完美时,重构出的时频域能量函数应当趋近于跳频函数WVD的自项分量。
本文在前人基础上提出一种优化的核函数。现将其定义为:
式中:a、b、c、d为自适应参数。c=d=1时,此核函数退化为前人设计的核函数[6],可以看做是本研究中优化后的核函数的一个特例。接下来对4个参数进行分析。
由于rect(·)控制时延方向的核函数宽度,当频偏为0时,时延轴只存在自项,因此参数b的取值为2TH时,能最多地保留自项分量。参数c、d决定了核函数的弧度,与a参数共同决定了核函数的纹理与形状。由于Sa(·)在频域是振荡函数,核函数与a、b、d这3个参数并不存在单调递增或单调递减的关系,因此需要引入一种评价核函数优劣的评价机制。
3 基于熵测度评价的核函数优化
在时频域,一个信号的时频聚集性越强,其能量则更贴合信号真实的时频位置;而在时频聚集性相同,信号时频分布的交叉项能量越小,则时频分布的能量也能更多地集中在真实的信号项附近。因此,无论是时频聚集性,还是交叉项的严重程度,都可以通过时频平面上能量分布的稀疏性加以描述。信息熵能够非常好地判断时频分布的稀疏程度,进而评价时频分布的优劣。对于同一信号,通常希望其时频分布的信息熵尽量小。
当核函数参数取最优解时,能量域信息熵可以获得最小值[7]。这里使用一种归一化Renyi熵[8]对能量域进行不确定性测定。离散类时频分布的归一化α阶Renyi熵的定义如下:
式中:n=1,2,3,…,N;N表示时域采样点数;k=1,2,3,…,K;K表示频域采样点数;P(n,k)表示点处的能量。当α>1且α为奇数时,Renyi熵均可正确反映信号时频域能量分布的集中情况:为了降低运算量,通常α可取3,此时信号的3阶Renyi熵可以(n,k)写为:
4 估计跳频信号的参数
计算核函数参数取不同值时,能量域的Renyi熵,熵越小时对应的核函数参数就越接近最佳核函数参数,选择熵出现最小值时的核函数参数对跳频信号参数进行估计。参数估计算法的具体步骤如下:
(1)根据式(5),计算出跳频采样信号的解析信号 x(t)对应的窄带模糊函数 Ax(τ,ν);
(2)根据式(7)预置核函数并通过遍历等方法寻找能使式(9)中熵取得最小值的核函数参数;
(3)按照式(6)重构出跳频信号的WVD函数Px(t,f);
(4)计算重构出的WVD函数在每一个采样时刻n上沿频率轴的能量最大的2%的能量值之和,获得矢量y(n);
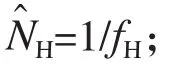
(6)将y(n)出现波峰的位置记为p(m),m=1,2,3,…,k,k为峰值的个数;
(7)估计跳变时刻:先求出峰值出现的平均位置:
再求出频率跳变时刻:
(8)估计跳频信号的频率集:
式中:l=1,2,3,…,L;L表示估计出的跳频频点个数。
5 仿真实验
为了验证优化后的核函数在跳频信号参数估计中的有效性,现对该算法进行仿真。已知一段跳频信号,其频点为0.52 kHz、1.5 kHz、0.24 kHz、1.82 kHz、0.82 kHz、2.24 kHz、1.20 kHz, 采 样 频率10 kHz,跳频周期为0.05 s,跳频时刻为0.02 s,采样时间0.35 s。原始跳频信号的WVD图像如图1所示,可以清晰地看见时频能量域存在大量的交叉项,虽然很难直接将交叉项与自项直接区分开,但WVD的时域边缘分辨率高的优势非常明显。
现分别在信噪比SNR=15 dB和SNR=-3 dB的环境下,进行跳频信号参数估计的仿真实验。
当SNR=15 dB时,信号的模糊函数如图2所示,图中信号的自项主要集中分布在模糊函数域的原点附近,且能量幅值较大,而大量交叉项则呈现出远离模糊函数域原点的对称分布。现将核函数参数设计为a=4、b=119、c=1、d=1,对跳频信号的模糊函数用核函数加权后,如图3所示,远离原点的大部分交叉项可以直接滤除,但自项附近依然存在残留的交叉项。将模糊函数域的能量分布进行二维FFT,使其转换到时频分布域,如图4所示。即可清晰地观察到时频域内信号的能量分布情况,由图4可以看出信号有6个完整的跳及1个不完整的跳。将图4与图1对比后发现,信号的跳频周期及各跳对应的频点相对准确。由信号在各时刻的沿频率轴的能量峰值图像(图5)可以较为准确地读取该跳频信号的跳频周期及各频点,同时也可以计算出跳频时刻为0.02 s。
当SNR=-3 dB时,信号的WVD图像如图6,与原始信号的WVD图像相比,前者的自项与交叉项出现了严重的混叠现象,难以直接分辨。现将核函数参数设定为a=3、b=119、c=0.05、d=1.2,获得加核函数后的信号模糊函数如图7所示,进行二维傅里叶变换后如图8所示,可以看出较为模糊的跳频信号时频图像,再将图像重构到时间-能量图上时,如图9所示,信号的跳频周期、频点及跳频时刻等参数均无法直接从图像中获取。此时对根据跳频信号参数估计的过程,最终恢复出跳频周期为0.049 s,频点为0.528 kHz(+0.008 kHz)、1.495 kHz(-0.005 kHz),0.254 kHz(+0.014 kHz)、1.822 kHz(+0.002 kHz),0.802 kHz(-0.018 kHz)、2.223 kHz(-0.017 kHz)、1.260 kHz(+0.006 kHz),跳频时刻为0.022 s。
为了验证新设计的核函数比原核函数具有更优化的性能,现分别计算两个核函数的3阶Renyi熵与信噪比的关系图。如图10,当原始跳频信号完全相同时,分别计算a阶Renyi熵;当熵相同时,在0 dB附近,优化的核函数可以获得3 dB至5 dB的性能增益。
6 结 语
跳频信号使用WVD方法进行参数估计时,最亟需解决的就是交叉项滤除的问题。本文提出的优化的核函数是前人研究基础上,受跳频信号自项具有时域有限支撑、频域无限拓展的特性启发[9],将原有核函数中的一次函数优化为平滑的可变幂函数,使核函数形状与信号自项更贴合,从而保留更多自项并滤除更多的交叉项。
本文中提出的核函数,依然存在进一步优化的空间,例如将函数设计为自适应核函数,将认为改变核函数参数优化为根据信号特点主动优化参数。另外,虽然在本算法中使用优化后的核函数比原算法获得了3 dB以上的性能提升,但其使用范围依然局限于高信噪比的环境中,在-10 dB以上的较低信噪比区间,能量峰值的个数及位置均不够准确,需要进一步辨别优化。-10 dB以下的低信噪比环境,几乎无法使用此算法准确地重构跳频信号的WVD并估计跳频、跳速及跳频时刻等参数。因此,在低信噪比环境下,如何改进时频分析类算法来估计跳频信号的参数,依然是一个艰难的挑战。

