中国股市波动率预测——基于已实现EGARCH模型和已实现SVL模型的实证比较研究

吴鑫育，王小娜，王海运

（安徽财经大学 金融学院，安徽 蚌埠 233030）

1 研究现状

研究金融资产的波动率对资产组合配置、风险管理与期权定价等都具有重要意义。学者们已经提出各种方法对波动率进行估计和预测，传统上，对金融资产波动率的建模主要基于2类模型：广义自回归条件异方差（GARCH）模型［1］和随机波动率（SV）模型［2］。但是，传统的GARCH模型与SV模型在描述金融市场的波动性时仍存在一定的局限性。大量的实证研究结果表明，资产未来波动率对当前正、负收益率（利好和利空消息）的反应是不对称的：当资产收益率为负时，未来波动率增加的幅度要大于资产收益率为正时的情形。Black［3］和Schwert［4］从杠杆效应的角度解释了这种非对称的波动率特性。随后，文献［5－7］为了研究股票市场中波动率的非对称性（杠杆效应），提出了指数GARCH（EGARCH）模型、GJRGARCH模型和门限GARCH（TGARCH）模型。文献［8－12］发现非对称GARCH模型比标准的GARCH模型具有更好的波动率预测效果。同样的，Yu［13］认为基本的SV模型可能对资产价格序列限制过多，除非考虑了金融杠杆效应的因素，于是将杠杆效应引入到SV模型，构建了杠杆SV（SVL）模型，并利用S＆P500指数进行了实证检验，发现该模型具有更好的样本内拟合效果。Ozturk等［14］通过运用SVL模型，发现选取的所有24只股票都存在显著的杠杆效应，且该模型显著提高了波动率的可预测性。Chen等［15］和Hong等［16］则分别探讨了将杠杆效应纳入SV模型对原油市场波动性建模以及期权定价的重要性。Mao等［17］推导出了捕获金融收益中杠杆效应的一般非对称随机波动模型的统计特性，实证结果表明，相比于传统的SV模型，考虑非对称性的SV模型提供了所选取的标普500指数样本在所有日期中的可靠预测。

近年来，伴随着高频金融数据的易获得性，在已有的波动率模型中加入高频信息变量已成为研究热点。Hansen等［18］在GARCH模型中加入基于高频数据构建已实现测度，提出了已实现GARCH（RGARCH）模型，实证结果表明该模型优于传统的GARCH模型。但是，该模型对杠杆效应的描述仍然不够充分。基于此，Hansen等［19］在RGARCH模型基础上进一步提出了已实现的EGARCH（REGARCH）模型，同时实证研究发现该模型以更好的经验拟合形式验证了新结构的优势。随后，Huang等［20］和Wu等［21］将REGARCH模型分别应用在期权定价和风险价值（VaR）测度上，发现该模型比RGARCH模型得到的预测结果更准确。同时，Takahashi等［22］将已实现测度引入到SV模型，又利用贝叶斯估计方法进一步提出了带杠杆的RSV（RSVL）模型。随后，Shirota等［23］将RSV模型与杠杆效应和长记忆特性相结合，对RSV模型进行了扩展，发现提出的新模型相对于RSV模型有更好的波动率预测表现。Li等［24］在RSV模型中加入杠杆效应和动态漂移，实证发现非对称RSV模型不仅可以改善波动率的拟合效果，同时在预测峰度、厚尾以及预测高阶自相关等动态性方面均具有更强的能力。文献［25－27］也对具有杠杆效应的RSV模型做了进一步研究。

然而，上述R（E）GARCH模型和RSV（L）模型大多假设收益率的新息服从标准正态分布。研究结果表明，金融资产收益率序列普遍具有尖峰厚尾和偏斜的特征［28－31］。考虑到该问题，王天一等［32］将RGARCH模型推广到具有厚尾分布的情形，发现厚尾分布可以改进RGARCH模型对市场风险的预测。王朋吾［33］以上证综指数和深证成指为样本，分别使用正态分布下和t分布下的GJR－GARCH模型和EGARCH模型研究波动率的非对称性特征，发现t分布状态比正态分布有更好的模型估计效果。黄雯等［34］认为RGARCH模型在偏斜t分布下的拟合效果和尾部风险描述能力均明显优于正态分布和t分布下的RGARCH模型。魏正元等［35］研究认为误差项服从偏斜t分布的RGARCH（1，2）模型对上证380指数的拟合能力较好，并能精确测量其收益率风险。玄海燕等［36］使用上证综合指数2016—2017年的高频数据分别比较了基于正态分布、t分布和偏斜t分布下REGARCH模型的拟合情况，发现偏斜t分布下REGARCH模型的拟合效果最优。

类似地，对于RSV（L）模型，Nugroho等［37］提出同时具有非对称效应和不同误差分布的非线性RSV模型，研究结果表明具有偏斜t分布的模型最适合描述东证股价指数数据。Takahashi等［38］在Takahashi［22］提出的RSVL模型的基础上进行扩展，将金融资产的收益率新息假设为服从偏斜t分布，利用美国的道琼斯工业平均指数和日本的日经225指数进行实证研究，发现与之前的正态分布下的RSVL模型相比，扩展模型改善了波动性和分位数预测，特别是在一些波动率较大的时期。Nugroho等［39］在提出的一种新的RSV模型中分别将信息服从正态分布和学生t分布进行比较，发现正态分布下的模型能够很好地捕捉波动性，而学生t分布的优势明显有限。国内目前针对RSV模型的研究还较少，吴鑫育等［40］提出了带学生t分布的门限RSV模型，并针对我国股票市场进行了实证研究。

基于以上分析可以发现，已有文献针对R（E）GARCH模型与RSV（L）模型的研究已经很充分，但对REGARCH和RSVL模型的对比，尤其是样本外的对比研究目前在国内外还鲜有发现。因此，本文中选取两类波动率模型（REGARCH模型和RSVL模型），同时考虑不同分布（正态分布、学生t分布与偏斜学生t分布）设定，构建6种波动率模型进行对比分析；选取我国上证综合指数2001—2018年共18年的样本数据，根据构建的6种波动率模型同时对我国股票市场的样本内拟合及其样本外预测表现进行比较研究；将样本外预测总样本分成2个子样本，即高波动时期和平稳的低波动时期，其中以包含2015年中国股市崩盘在内的2014—2016年作为高波动时期的代表，以平稳的2016—2018年作为低波动时期的代表，分别对这6种模型进行预测性能的比较；通过上述比较研究，试图找出适合我国股票市场的波动率模型，从而为学者和金融机构今后选择恰当的波动率模型进行更加准确的波动率预测、风险价值评估和金融衍生产品定价提供参考。

2 模型及其估计

2.1 标准REGARCH模型

REGARCH模型由Hansen和Huang［19］提出，该模型相比RGARCH模型可以更灵活地捕获杠杆效应。标准的REGARCH模型的形式为：

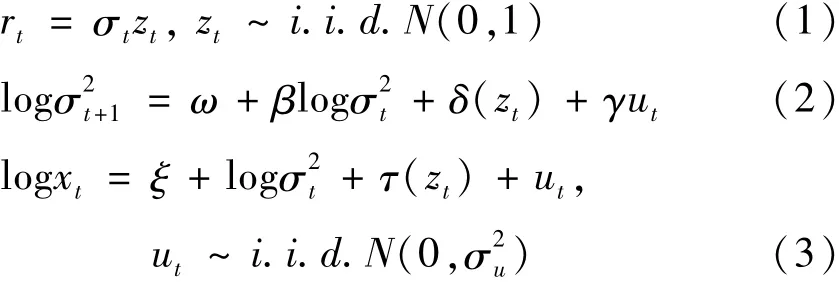
其中：rt是t时刻的资产收益率；是条件方差，It－1表示资产收益率在到t－1时刻之前所有信息的集合；β是波动率的持续性参数。状态方程（2）保持平稳的条件为β＜1。新息zt与度量误差ut之间相互独立，假设zt服从标准正态分布。τ（zt）和δ（zt）是杠杆函数，满足：

其中：δ1，τ1＜0用于捕捉过去正、负收益率变化对未来波动率的非对称影响（杠杆效应）。

度量方程（3）中xt为已实现测度，ξ是为了修正由于存在非交易时间和市场微观结构噪声等原因造成的波动率在已实现测量时的偏差。当ξ＝0时，已实现测度是真实波动率的无偏估计，当ξ＜0时，已实现测度下偏，表明非交易时间对已实现测度的影响大于市场微观结构噪声对已实现测度的影响，反之亦然。

2.2 标准RSVL模型

其中：rt是t时刻的资产收益率；σt≡exp（θt／2）是波动率；θt是资产收益率的对数波动率；ht是均值调整后的对数波动率；φ用来度量波动率的持续性。状态方程（5）保持平稳的条件为φ＜1。度量方程（6）中xt为已实现测度，ξ为偏差修正项，意义与式（3）相同。新息zt和ηt之间存在相关性，相关系数为ρ，即：

相关系数ρ可以反映资产收益率与未来波动率之间的非对称关系。从经验研究来看，这种非对称性具有显著的负相关性，即资产收益率的负向冲击将会导致波动率更大幅度的增加。

2.3 其他分布设定

上述标准的REGARCH模型和RSVL模型均假设资产收益率的新息zt服从标准正态分布，但在实际金融市场中，金融时间序列往往表现出尖峰厚尾和偏斜的特征，新息为标准正态分布的设定仍无法充分刻画这种特性。基于此，除考虑资产收益率的新息服从标准正态分布外，还分别考虑可以刻画尖峰厚尾特征的标准学生t分布和能够同时刻画尖峰厚尾和偏斜特性的标准偏斜学生t分布。

1）标准学生t分布密度函数

2）标准偏斜学生t分布密度函数

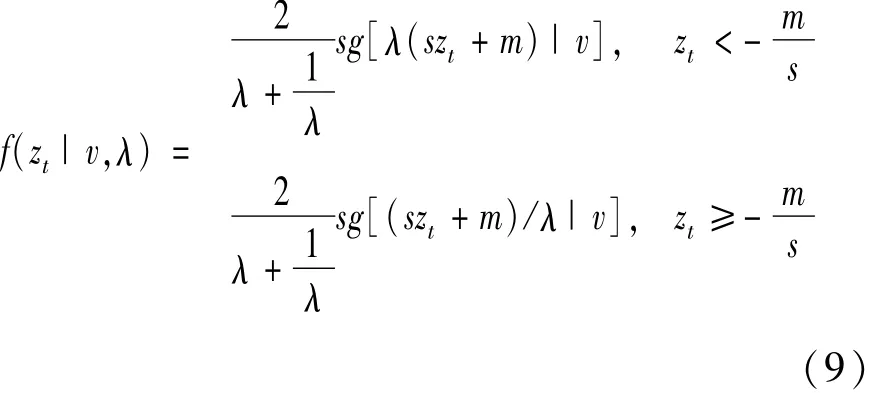
其中：

由此，利用REGARCH和RSVL两类模型分别结合标准正态分布（N）、标准学生t分布（t）、标准偏斜学生t分布（SKt）3种收益率新息分布，构建如表1所示的6种实证模型。

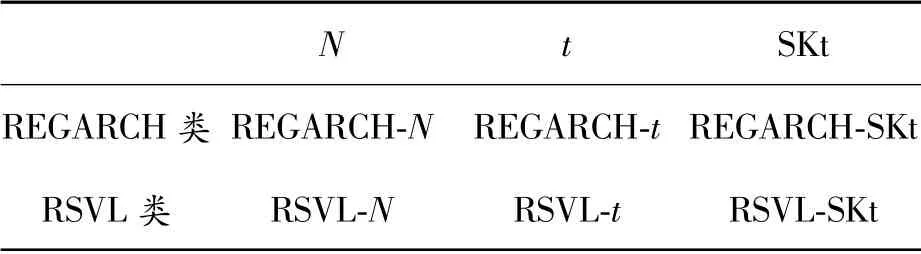
表1 实证模型

2.4 模型参数估计

为了估计REGARCH模型和RSVL模型的参数，使用经典的极大似然方法。由于REGARCH模型的条件方差是模型参数和历史新息的确定性函数，其似然函数可以直接写出：

其中Θ是模型参数向量。

但对于RSVL模型，由于波动率由一个新的随机过程驱动，导致模型的似然函数变得非常复杂，其形式为：

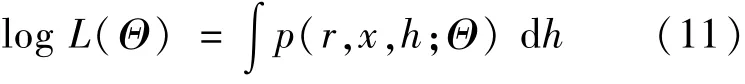
其中p（r，x，h；Θ）是r，x和h的联合概率密度函数。可以发现，式（11）是一个复杂的高维积分，不能直接求解。为了解决这个问题，使用灵活且易于实现的连续粒子滤波方法来估计RSVL模型的似然函数式（11），具体参见文献［41－42］。

在得到REGARCH和RSVL模型的似然函数后，模型参数即可通过最大化对数似然函数得到，即：

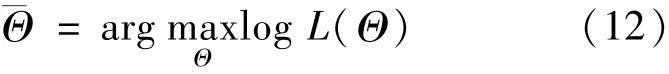
3 实证研究

3.1 数据

选取上证综合指数（SSEC）作为中国股票市场的代表，研究采用的数据包括SSEC的日收盘价与已实现核。数据来自于Oxford-Man Institutes Realized Library。样本的跨度范围是2001.01.02—2018.12.31，包含4 347个交易日的观测值。选择Barndorff-Nielsen等［43］提出的已实现核作为已实现测度，因为与传统的已实现方差相比，已实现核不仅能更充分地利用日内信息，同时对微观结构噪声具有很好的稳健性。

图1显示了SSEC日收盘价、收益率、已实现核及其分布。

图1 SSEC日收盘价、收益率、已实现核及其分布曲线

从图1（b）的日收益率和图1（d）的已实现核可以观察到，SSEC收益率序列在总样本期间表现出显著的波动率的时变性和聚集性等特征；从图1（c）的经验收益率密度和图1（e）的收益率Q－Q图来看，收益率序列具有典型的尖峰厚尾和偏离正态分布的特征。值得注意的是，图1（f）的对数已实现核Q－Q图表明其接近于正态分布。

表2给出了SSEC日收益率、已实现核及其对数形式的描述性统计量。可以发现：SSEC日收益率的分布呈现出负偏（偏度小于0）和尖峰（标准正态分布的峰度为3）、且拒绝正态分布的原假设（Jarque-Bera统计量显著）的特征；已实现核则表现为正偏和更尖的峰度，Jarque-Bera统计量的值也非常大。但将已实现核取对数之后，其偏度、峰度和Jarque-Bera统计量的值均明显变小，更重要的是，其峰度接近于3，与图1（f）的对数已实现核的Q－Q图结果一致，即对数已实现核时间序列接近于正态分布。因此，在度量方程中，将对数已实现核波动的新息假设为服从正态分布符合实际情况。

表2 SSEC日收益率与RK描述性统计量

3.2 参数估计结果

通过采用SSEC数据，利用极大似然估计方法得到6种模型的参数估计结果如表3～4所示。由表3可以发现，REGARCH模型在3种分布下β值均接近于1，说明SSEC具有很高的波动率持续特性。REGARCH模型在3种分布下的δ1值和τ1值均小于0，能够很好地用于捕捉正向和负向收益率变化对未来波动率的非对称影响（杠杆效应）。控制着收益率尾部形状的参数v均大于2，λ均小于1，也再次验证了SSEC收益率分布具有尖峰厚尾以及偏斜的特征。另外，偏差修正项ξ均小于0，说明已实现核存在下偏，即非交易时间对已实现核的影响大于市场微观结构噪声对已实现核的影响。从对数似然函数值LL和信息准则AIC与BIC来看，REGARCH-SKt模型拟合效果优于同类型的REGARCH-N模型和REGARCH-t模型。

表3 REGARCH模型参数估计结果

由表4可以发现，RSVL模型在3种分布下φ值均接近于1，再次验证了SSEC具有很高的波动率持续特性。同时，偏差修正项ξ也都小于0。不同误差分布下的3种RSVL模型的ρ值均小于0，能够反映出收益率与未来波动率之间的杠杆效应，且符合以往的经验研究，即这种非对称性具有显著的负相关性，资产收益率的负向冲击会导致更大的波动性。形状参数v均大于2，λ均小于1。从对数似然函数值LL和信息准则AIC来看，RSVL-SKt模型样本内拟合效果优于同类型RSVL-N和RSVL-t模型。但从信息准则BIC来看，RSVL-N模型的BIC值相对于RSVL-SKt模型要小11个点（而RSVL-SKt的AIC值相对于RSVL-N模型小于不到1个点），且Wang等［44］发现就嵌套模型而言，信息准则BIC优于AIC。因此，综合来看，RSVL-N模型具有最好的样本内拟合效果。

表4 RSVL模型参数估计结果

结合表3、4的似然函数和信息准则可以发现，REGARCH-SKt模型的样本内拟合效果达到最优。

3.3 样本外预测

采用固定时间窗口为3 200的滚动时间窗方法对模型进行滚动估计以及向前一天的样本外波动率预测。因为股票市场不可能一直“风平浪静”，有时会因宏观政策调控或者其他外部环境因素的冲击导致股票市场产生异常值，一段时期内波动居高不下。为了更全面系统地比较以上6种模型在不同波动时期的样本外预测表现，除考虑模型在预测总样本（1 147个样本）的表现，同时将预测总样本分解为2个子样本，即包含2015年中国股市崩盘的2014—2016年的高波动时期（600个样本）以及2016—2018年的低波动时期（547个样本）分别进行样本外预测的比较。

3.3.1 损失函数

为评价各模型波动率预测的准确性，使用2个稳健的损失函数，即均方误差（mean squared error，MSE）函数和拟似然（quasi-likelihood，QLIKE）函数进行样本外预测性能的比较。2个损失函数表达式为：

从表5的预测总样本期来看，在任何一种误差分布下，相比于RSVL模型，REGARCH模型均具有更优的样本外预测性能。另外，REGARCH模型同时在标准正态分布和标准偏斜t分布下具有较好的样本外预测效果，而RSVL模型在偏斜t分布下的样本外预测表现明显最好。

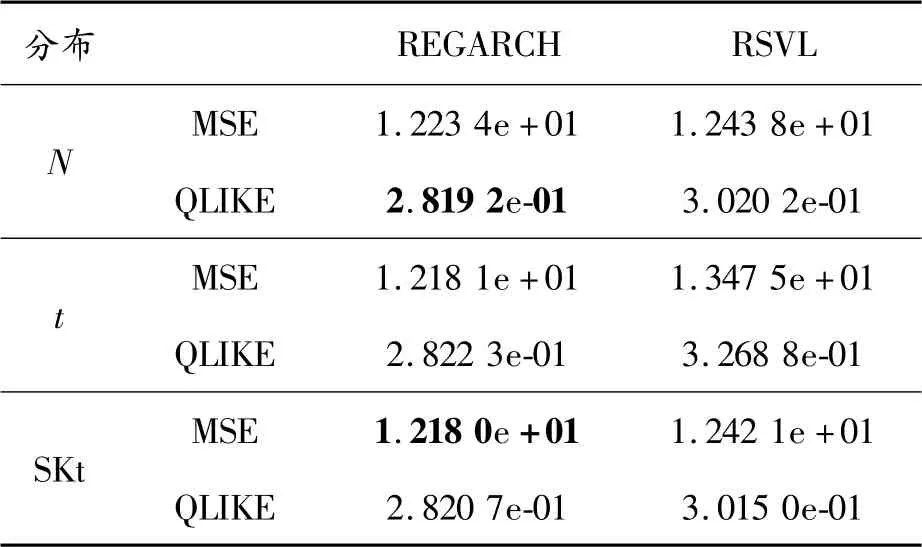
表5 样本外预测结果：预测总样本期

从表6的高波动预测期来看，在不同误差分布下，REGARCH模型相比于RSVL模型仍然具有更好的样本外预测效果，与预测总样本期的表现一致。此外，相比于正态分布与学生t分布，REGARCH模型与RSVL模型均在偏斜t分布下的样本外预测性能更好。

表6 样本外预测结果：高波动期

从表7的低波动预测期来看，在不同误差分布下，RSVL模型超越REGARCH模型表现出更好的样本外预测效果。另外，REGARCH模型在标准正态分布下的样本外预测性能相对于其他分布下更加优越，与高波动期结论相反。而RSVL模型在标准正态分布和标准偏斜t分布下具有同样的样本外预测效果，且RSVL模型在偏斜t分布下的预测效果不如预测总样本期和高波动期稳健。

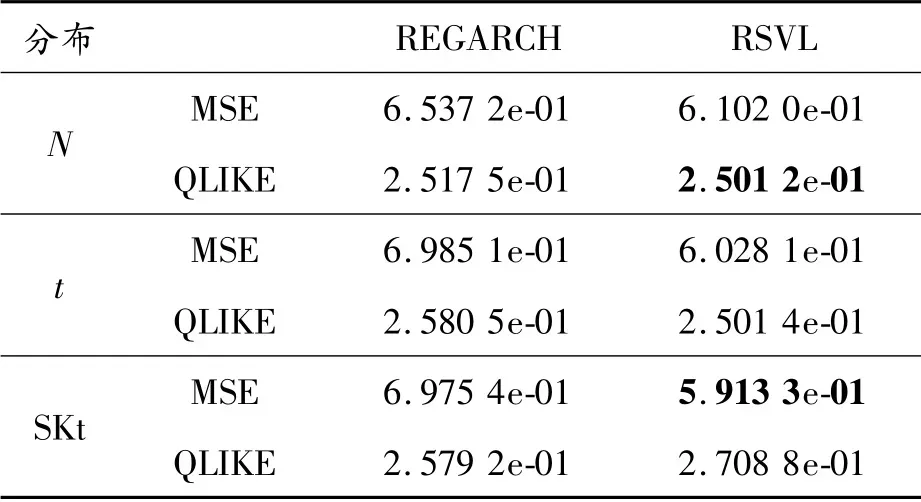
表7 样本外预测结果：低波动期

3.3.2 MCS检验

MSE和QLIKE损失函数虽然可以作为模型比较预测能力的标准，但却不能仅凭借其值就判断模型预测能力的优劣，因为2个模型的预测误差之间的差异可能并不显著。因此，为了更好地比较上述6种模型之间预测精度的差异，保证预测结论更加稳健、可靠，同时使用Hansen等［46］提出的模型信度设定检验（model confidence set，MCS）实证分析6种波动率模型对中国股票市场实际波动特征的刻画能力和预测精度。为了得到MCS检验中的各统计量及P值，选取模拟次数10 000次作为自举（bootstrap）过程的控制参数。参照Hansen等［46］方法，MCS检验的显著性水平α取值为0.1，那么P值小于0.1的波动率模型是样本外预测能力差的模型，将在MCS检验过程中被剔除；而P值大于0.1的波动率模型则是样本外预测能力较好的模型，因此在MCS检验过程中能幸存下来。

从表8预测总样本期可以发现：在3种误差分布下，REGARCH模型的P值均大于RSVL模型，说明REGARCH模型有更好的预测性能。另外，REGARCH-N模型在QLIKE损失函数下的预测效果最好（P值为1），REGARCH-SKt模型在MSE损失函数下的预测效果最好。

表8 MCS检验结果：预测总样本期

从表9高波动期可以看到，高波动期与预测总样本期的预测结果几乎一致，只是此时REGARCH-SKt模型在2种损失函数下的P值全部为1，说明REGARCH-SKt模型相对于其他5种波动率模型有更好的样本外预测效果。

表9 MCS检验结果：高波动期

从表10低波动期可观察到，在3种误差分布下，RSVL模型的P值均大于REGARCH模型，因此RSVL模型具有更好的预测效果，取代了REGARCH模型在预测总样本期和高波动期的表现。另外，RSVL-N模型在QLIKE损失函数下P值为1，但在MSE损失函数下P值为0.001 0（小于0.1）；RSVLSKt模型在MSE损失函数下P值为1，但在QLIKE损失函数下P值为0.0310；而RSVL-t模型无论在哪种损失函数下，其P值都最接近于1。因此，RSVL-t模型具有最稳健的样本外预测效果。

表10 MCS检验结果：低波动期

综上可以发现，表8～10的结论与表5～7相应的结论是对应一致的，说明所得结论是稳健的。

4 结论

采用SSEC作为中国股票市场的代表，对REGARCH模型和RSVL模型在3种不同误差分布（正态分布，学生t分布，偏斜t分布）以及样本外阶段（预测总样本期、高波动期与低波动期）下的波动率预测表现进行实证比较分析。通过研究发现，在上述3种误差分布下，REGARCH模型的拟合效果均优于RSVL模型，其中具有尖峰厚尾和偏斜特征的REGARCH-SKt模型的样本内拟合效果优于同类型的REGARCH-N、REGARCH-t模型，该结论与玄海燕等［32］结论一致；在预测总样本期，REGARCH模型在3种误差分布下的样本外预测效果均优于RSVL模型，其中REGARCH-N模型和REGARCH-SKt模型同时具有较好的样本外预测效果；在高波动期，样本外预测效果与总样本期表现几乎一致，只是此时REGARCH-SKt模型的样本外预测性能变得更稳健且达到最优；在低波动期，样本外预测效果的表现几乎与上述两个时期相反，即RSVL模型取代了REGARCH模型在不同误差分布下均具有最好的样本外预测效果的表现，其中RSVL-N模型和RSVL-SKt模型同时具有较好的样本外预测效果，但RSVL-t模型的预测性能却是最稳健的。

本研究可进一步扩展，即针对REGARCH模型和RSVL模型在高、低波动期不同的预测表现，未来可根据实际金融资产的波动率在某个样本期间的高、低波动时段长度，选择合适的权重考虑将REGARCH模型和RSVL模型组合起来，构造一种混合的波动率模型，以期对波动率预测提供更加优越的结果。