广东省各城市经济发展质量综合评价研究

陈泳冰

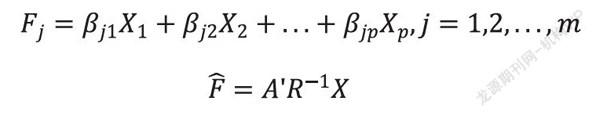
一、引言

广东是中国改革开放和现代化建设先行一步的地区，随着党的十九大作出中国经济已由高速增长阶段转向高质量发展阶段的重大判断，分析评价广东省各城市经济质量的发展状况，对推动全省整体经济的高质量发展具有重大意义。本文以广东省21个主要城市为研究对象，在“创新、协调、绿色、开放、共享”发展理念的基础上，构建了包含5个一级指标共14个二级指标的广东省经济发展质量评价指标体系，运用因子——聚类分析对广东省各城市的经济发展质量做出客观评价。

二、理论基础

（一）因子分析

因子分析是从研究变量内部相关的依赖关系出发，将具有错综复杂关系的变量综合为较少的几个因子，体现原始变量和因子之间的关系，同时还可以根据不同因子对变量进行分类。因子分析通过对变量的相关系数矩阵内部结构的研究，找出少数几个随机变量去描述多个变量之间的相关关系。然后根据相关性的大小把变量分组，使同组内变量间的相关性较高，不同组间的变量相关系较低。

因子分析的数学模型为：

其矩阵形式为：

且满足：

其中，是可实测的p个指标所构成的p维随机向量，是X的公共因子;为因子载荷，是第i个变量在第j个公共因子上的负荷;矩阵A为因子载荷矩阵;称为X的特殊因子。

在因子模型中，用回归的思想求出线性组合系数的估计值，即建立如下以公共因子为因变量、原始变量为自变量的回归方程：

此处原始变量与公共因子变量均为标准化的，因此回归方程中没有常数项。在最小二乘意义下，可以得到F的估计值：

（二）系统聚类分析

系统聚类法首先将每个样品单独看成一类，在规定类间距离的条件下，选择距离最小的一对合并成一个新类，并计算新类与其他类之间的距离，再将距离最近的两类合并，这样每次会减少一类，直到所有的样本合为一类为止。本文主要使用类平均法来定义类间距离。

类平均法定义两类之间的距离平方为这两类元素两两之间距离平方的平均，即：

设聚类到某一步将和合并为，则任一类与的距离为：

三、实证研究

（一）经济发展质量评价指标体系构建

在借鉴关于构建经济质量发展评价指标体系已有研究文献的基础[1-3]上，基于“创新、协调、绿色、开放、共享”的发展理念，构建了包含经济发展、科研技术、居民生活、对外开放和绿色环保5个一级指标共14个二级指标的广东省经济发展质量评价指标体系。

其中，经济发展包含的二级指标有：人均GDP（X1）、第三产业占GDP比重（X2）、固定资产投资（X3）;科研技术包含的二级指标有：科技支出占GDP的比重（X4）、高新技术产品产值（X5）、专利授权量（X6）;居民生活包含的二级指标有：人均可支配收入（X7）、人均消费支出（X8）、国内旅游收入占GDP比重（X9）;对外开放包含的二级指标有：进出口总额（X10）和实际使用外资占GDP比重（X11）;绿色环保包含的二级指标有：城市人均公园绿地面积（X12）、城市公共交通车辆标准运营数（X13）、城市污水处理率（X14）。

（二）数据选取

依据构建的广东省经济发展质量评价指标体系，从《广东统计年鉴2020》中选取2019年广东省各城市相关数据。其中，城市污水处理率使用2018年的数据。

（三）因子分析

在SAS软件中调用因子分析程序，根据方差贡献率选取适当数量的因子作为初始因子。由于前5个因子的累计贡献率达到了94.3%，本文取前5个因子作为初始因子。由于因子载荷矩阵中元素的绝对值向0、1分化不明显，本文利用正交方差最大旋转法进行因子旋转，采用旋转因子作为最终的公因子。

最终的因子得分函数为：

F1=0.003Y1-0.062Y2+0.131Y3+0.065Y4+0.264Y5+0.221Y6+0.022Y7+0.009Y8-0.078Y9+0.266Y10-0.260Y11-0.135Y12+0.168Y13-0.001Y14;

F2=0.282Y1+0.053Y2-0.124Y3+0.259Y4-0.154Y5-0.166Y6+0.154Y7+0.190Y8-0.093Y9-0.176Y10+0.707Y11-0.232Y12-0.193Y13-0.140Y14;

F3=-0.054Y1+0.024Y2+0.198Y3-0.184Y4-0.167Y5-0.056Y6+0.116Y7+0.076Y8-0.096Y9-0.220Y10-0.217Y11+1.043Y12+0.097Y13-0.137Y14;

F4=-0.011Y1+0.712Y2+0.165Y3-0.147Y4-0.150Y5+0.037Y6-0.056Y7-0.025Y8+0.466Y9-0.094Y10+0.142Y11-0.089Y12+0.203Y13-0.012Y14;

F5=-0.090Y1-0.024Y2-0.196Y3-0.044Y4-0.089Y5+0.047Y6-0.077Y7-0.068Y8+0.073Y9+0.189Y10+0.002Y11-0.077Y12+0.014Y13+1.043Y14;

其中Yi是Xi標准化以后的变量。

以旋转后的方差贡献率为权数构造综合因子得分函数为：

F综=（6.723F1+2.726F2+1.405F3+1.269F4+1.080F5）/13.203

根据因子得分函数和综合因子得分函数，计算出广东省各城市的综合得分及各个公共因子得分，按照综合得分从大到小排列，得到广东省21个城市的综合评价结果（见表1）。

（四）聚类分析