色纱与色织物之间颜色相关性研究

王小艳 杜金梅 蒋阳 许长海

摘要： 为解决纱线色深不合格造成的色纱浪费问题，文章研究了不同颜色深度色纱与色织物之间颜色相关性，探讨了色深不合格的色纱织成织物后，织物颜色与目标织物颜色一致的可能性。结果表明，同深度色纱织成织物的颜色深度相较于纱线会降低;异深度色纱织物的颜色深度具有可预测性。对于平纹色织物，当经纬纱线的同色性指数在0.81～1.23时，异深度色纱织物与同深度色纱织物具有相同的预测模型，且要求预测偏差为2%时，准确率可达85.53%;同色性指数在此范围内的经纬色纱可被重新使用以得到色深合格的织物，从而避免浪费。

关键词： 色纱;色织物;颜色深度;同色性指数;颜色预测

中图分类号： TS151.9

文献标志码： A

Abstract： Colored yarns that are disqualified in color depths for yarn-dyed fabrics are usually discarded or left unused in current industry. In this paper， the color correlation between the colored yarns and yarn-dyed fabrics with different color depths was investigated， to explore the possibility that that the colors of fabrics woven from colored-yarns that were disqualified in color depths matched the colors of target fabrics. The results showed that the color depth of a fabric woven from colored-yarn with the same depth was lower than that of yarn， and the color depths of fabrics woven from colored-yarns with different depths was predictable. For a plain weave yarn-dyed fabric， when the homochromy index（K） of warp/weft yarn was 0.81-1.23， fabrics woven from colored-yarns with different depths and those with the same depth had the same color prediction model. When a prediction bias of 2% was required， the accuracy of prediction model was up to 85.53%. It was indicated that colored yarns that were disqualified in color depths within this homochromy index range can be reused to obtain fabrics qualified in color depths， to avoid waste.

Key words： colored yarns; yarn-dyed fabric; color depth; homochromy index; color prediction

色织物是由有色纱线织造而成的织物，年产量超30亿 m[1]。与印染布相比，色织物具有风格独特、色彩丰富、立体感强等特点[2-3]。用于色织物的色纱一般是通过筒子纱染色获得，但筒子纱染色很难控制筒纱的外层、中层及内层颜色深度完全相同[4]，且每一批筒子纱之间的颜色深度也有差异，这些都会造成染出的纱线颜色深度与目标纱线颜色深度不一致，即产生了颜色深度不合格的色纱[5-6]。为保证产品质量，色织厂通常将颜色深度不达标色纱丢弃或闲置，这造成了大量色纱的浪费[7]。

色织物的颜色不仅取决于经纬纱线的颜色，还与织物的组织结构密切相关[8-9]。所以，即使是同色的经纬纱线，织成织物的颜色与纱线的颜色也可能不同[10]。为了获得目标色的织物，需要对色纱的颜色进行筛选。这也提供了一种将色深与目标色深不一致的色纱交织来得到目标一致的色织物的思路。

通常情况下，为保证目标色织物的颜色均一性，会使用颜色深度相同的经纬色纱进行织造。本文以经纬同染料同深度（简称“同深度”）的色织物为目标色织物，拟利用一系列同染料异深度（简称“异深度”）的经纬色纱来模拟颜色深度与目标色纱颜色深度不一致的色纱，探究经纬异深度的色织物表观颜色与目标色织物表观颜色一致的可能性，以重新使用颜色深度不合格的色纱，降低色纱废弃量，节约成本。

1 试 验

1.1 材料、药品和仪器

材料：平均单强强力>440 cN的高强力棉紗（博茂纺织品有限公司）。

药品：活性红3BS、活性黄3RS和活性艳蓝KN-R（浙江龙盛集团股份有限公司），碳酸钠、氯化钠（分析纯，国药集团化学试剂有限公司）。

仪器：Datacolor 650型反射光分光光度计（美国Datacolor公司）。

1.2 方 法

1.2.1 试验样品的设计

以同染料不同染色深度的纱线来模拟色深不合格的色纱，并以这些纱线设计一系列平纹（1︰1）色织物。其中，经纱和纬纱的色深度相同或不同，纱线及织物各项参数为：纱线线密度为14.58×2 tex，捻度为7.1 捻/cm，单强强力为466 cN;织物的组织结构为平纹（1︰1），经纬密均为23.62 根/cm。

所设计色织物的经纬纱线的颜色深度通过控制纱线染色染料质量分数获得。染料质量分数为浅色（0～1%），中色1（1%～2%），中色2（2%～3%）和深色（3%～4%）。在每个染色质量分数范围内，每只染料按0.25%的染色质量分数梯度上染纱线。每只染料每个染色质量分数范围内包含8个样品，其中经纬纱线同质量分数的色织物和经纬纱线不同质量分数的色织物各4个，选择红、黄、蓝三种色相的染料。由于不同色相纱线混合会有空间混合效果，为了减少干扰因素，分别研究同一色相经纬纱线与织物颜色的对应关系，故共有96个色织物样本。色织物的经纬纱线染色质量分数组合如表1所示。

1.2.2 色织物样品的准备

委托江苏联发高端纺织技术研究所，根据试验样品设计进行染纱和织造，得到品质较高的色织物样品。

1.3 测试方法

1.3.1 纱线色样的颜色测试

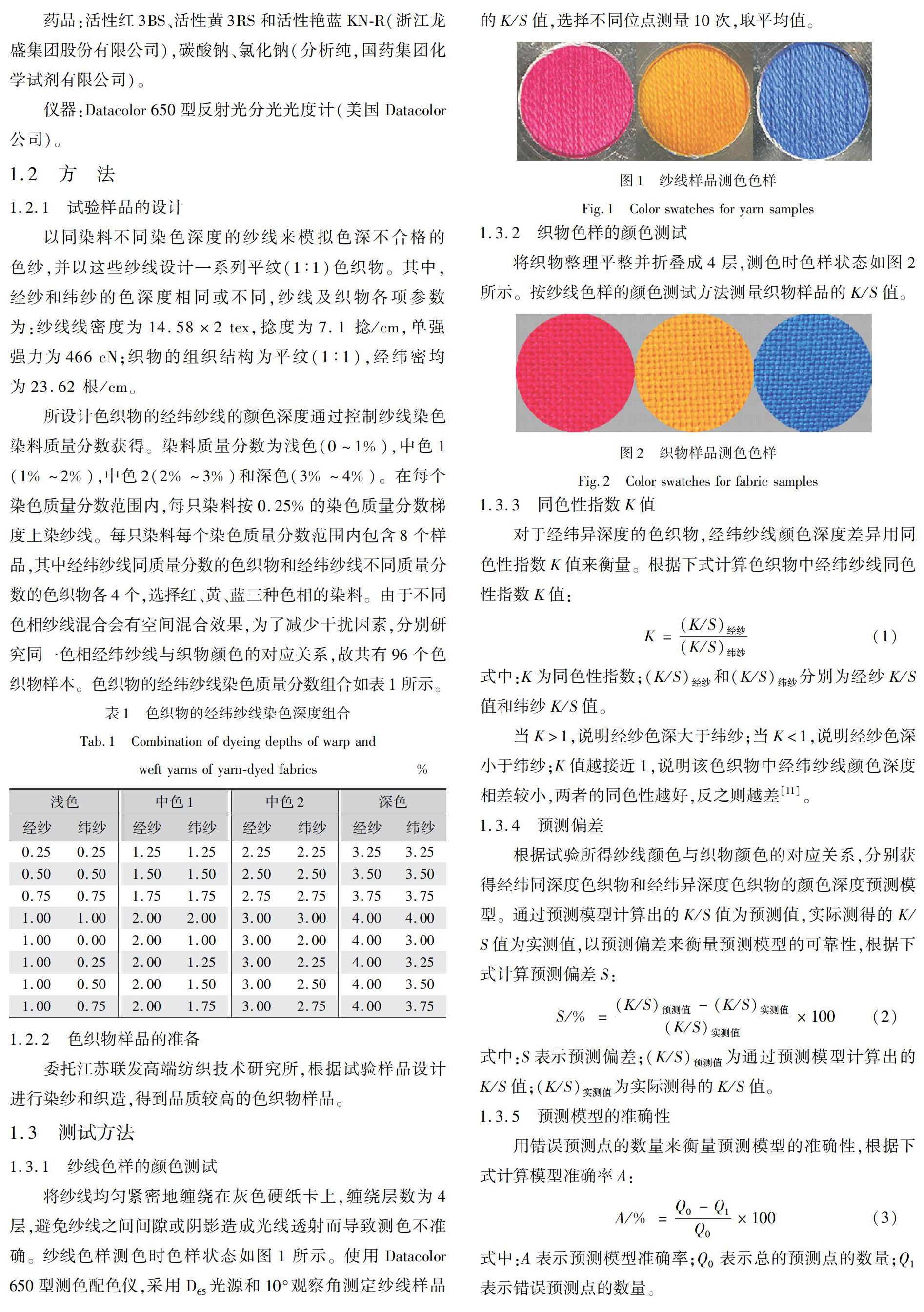
将纱线均匀紧密地缠绕在灰色硬纸卡上，缠绕层数为4层，避免纱线之间间隙或阴影造成光线透射而导致测色不准确。纱线色样测色时色样状态如图1所示。使用Datacolor 650型测色配色仪，采用D65光源和10°观察角测定纱线样品的K/S值，选择不同位点测量10次，取平均值。

1.3.2 织物色样的颜色测试

将织物整理平整并折叠成4层，测色时色样状态如图2所示。按纱线色样的颜色测试方法测量织物样品的K/S值。

1.3.3 同色性指数K值

对于经纬异深度的色织物，经纬纱线颜色深度差异用同色性指数K值来衡量。根据下式计算色织物中经纬纱线同色性指数K值：

K=（K/S）经纱（K/S）纬纱（1）

式中：K为同色性指数;（K/S）经纱和（K/S）纬纱分别为经纱K/S值和纬纱K/S值。

当K>1，说明经纱色深大于纬纱;当K<1，说明经纱色深小于纬纱;K值越接近1，说明该色织物中经纬纱线颜色深度相差较小，两者的同色性越好，反之则越差[11]。

1.3.4 预测偏差

根据试验所得纱线颜色与织物颜色的对应关系，分别获得经纬同深度色织物和经纬异深度色织物的颜色深度预测模型。通过预测模型计算出的K/S值为预测值，实际测得的K/S值为实测值，以预测偏差来衡量预测模型的可靠性，根据下式计算预测偏差S：

S/%=（K/S）预测值-（K/S）实测值（K/S）实测值×100（2）

式中：S表示预测偏差;（K/S）预测值为通过预测模型计算出的K/S值;（K/S）实测值为实际测得的K/S值。

1.3.5 预测模型的准确性

用错误预测点的数量来衡量预测模型的准确性，根据下式计算模型准确率A：

A/%=Q0-Q1Q0×100（3）

式中：A表示预测模型准确率;Q0表示总的预测点的数量;Q1表示错误预测点的数量。

2 结果与分析

2.1 经纬同深度纱线与其织物的颜色深度關系

2.1.1 经纬同深度纱线与其织物的K/S值曲线关系

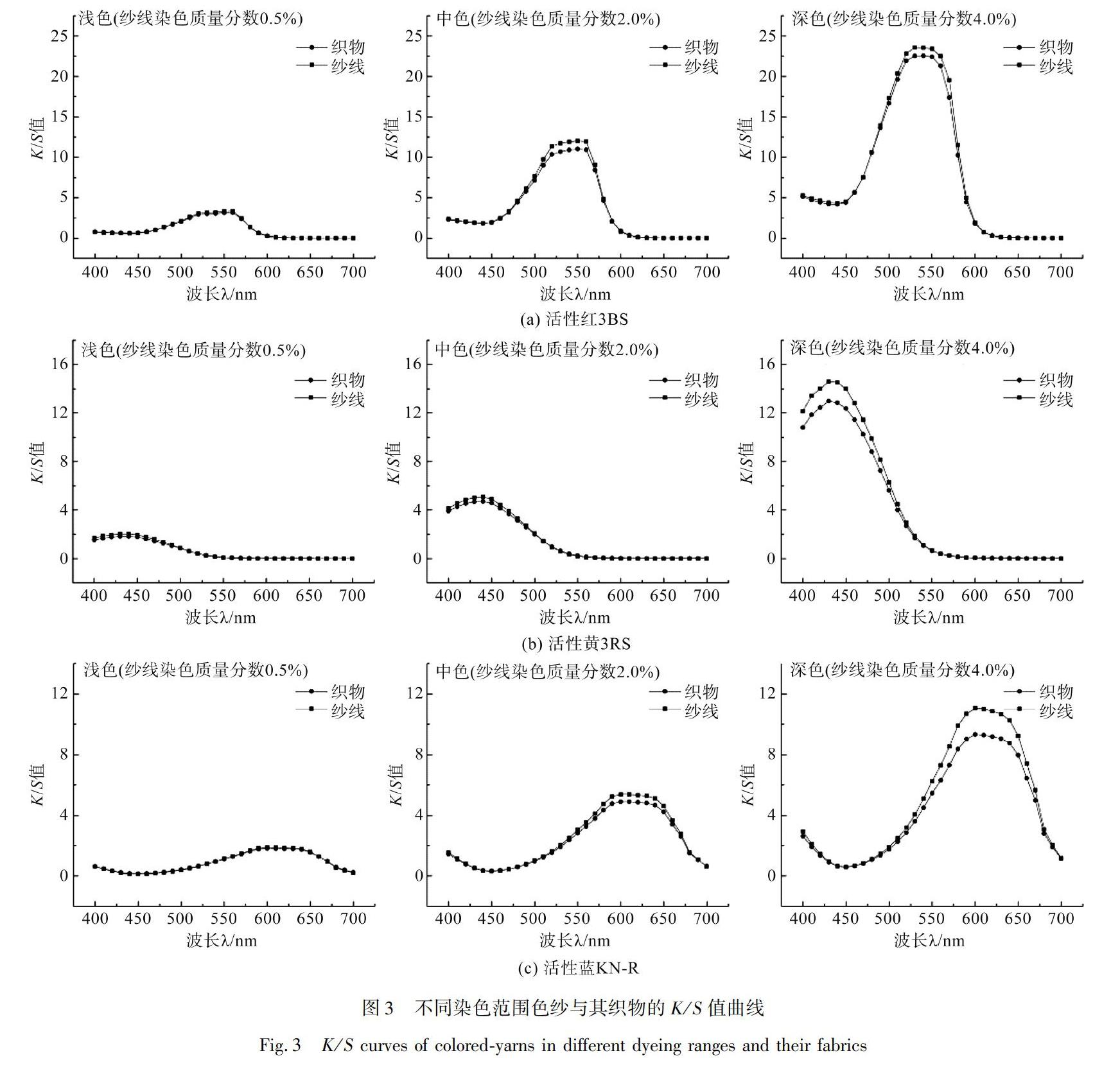
同深度色纱交织成织物过程中的颜色变化主要是由织物组织结构引起的。为了探究从纱线到织物转变过程中由于织物组织结构产生的颜色变化，对不同染色质量分数范围内的经纬同深度染色纱线及其织物的K/S值曲线进行对比，结果

如图3所示。

由图3可以看出，同染料同深度色纱与其织成织物的K/S值曲线形状一致，最大吸收波长的位置不变，但色纱的最大吸收强度（K/S值）高于织物，在中色和深色时这种最大吸收强度差异尤为明显。说明同染料同深度色纱交织成织物过程中，颜色色相没有发生明显的变化，但颜色深度发生了变化，且颜色深度的变化程度在各个染色深度范围有所差别。

2.1.2 经纬同深度的色织物颜色预测模型

根据同深度色纱与其织物K/S值曲线的关系，选用最大吸收波长处的K/S值为同深度色纱交织物的过程中颜色深度变化的衡量指标，以建立一个简明的经纬同深度的色织物颜色预测模型，达到由纱线K/S值预测织物K/S值的目的。

由于经纬同深度色织物的经纱和纬纱颜色一致，所以可以用经纱和纬纱的K/S值平均值作为纱线的K/S值，每个纱线的K/S值对应一个由此经纬纱线织成织物的K/S值。对活性红3BS、活性黄3RS和活性艳蓝KN-R三只染料上染的纱线的K/S值与其织物的K/S值作图，每只染料对应16个样品点，共48个样品点，并对散点图进行拟合，结果如图4所示。

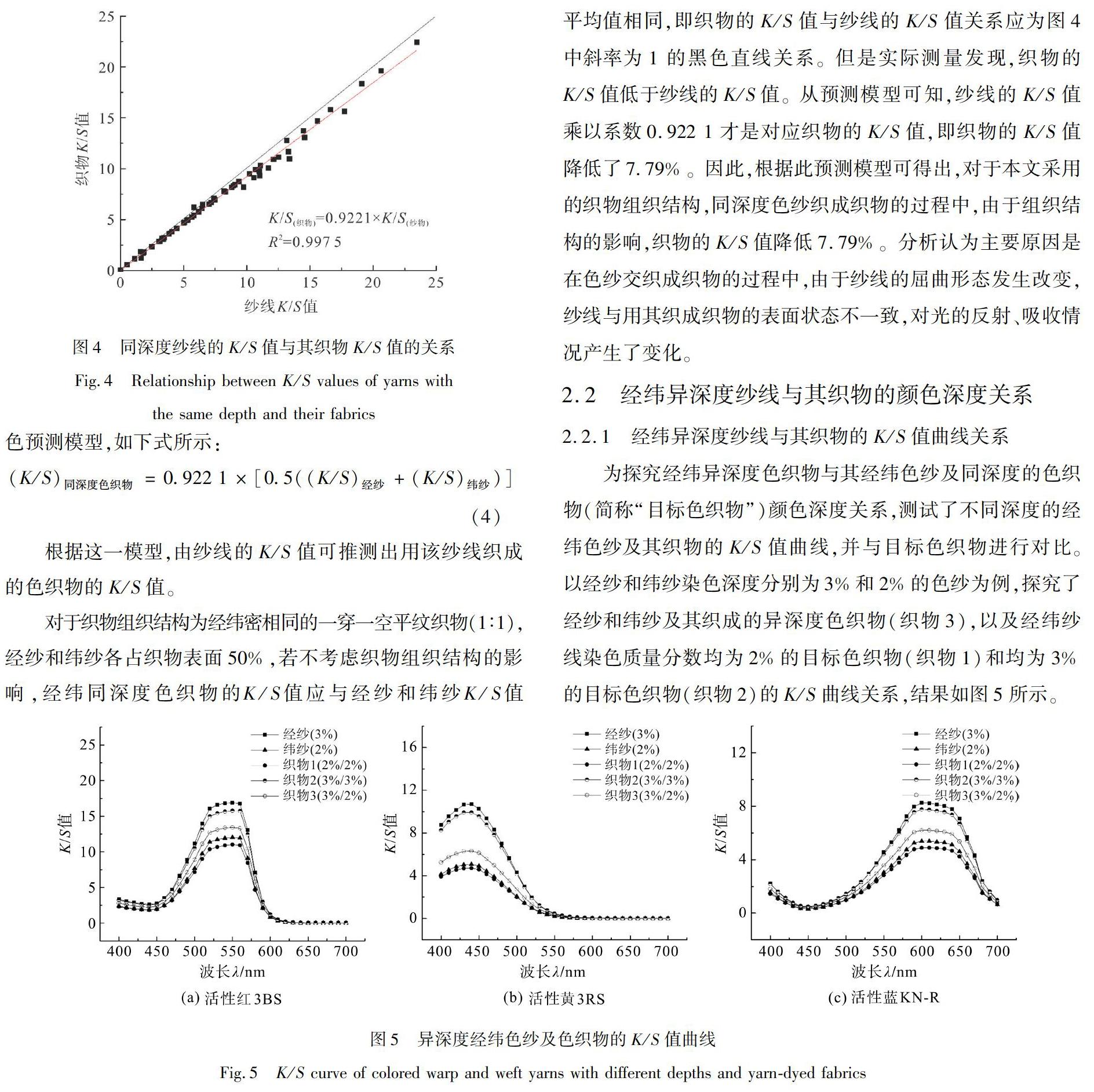
由图4中的拟合直线可以看出，织物K/S值随其纱线的K/S值呈线性变化，拟合系数大于0.990 0，说明它们具有良好的线性关系。其中，斜率为0.922 1，截距为0。由此，以最大吸收波长处的K/S值为纽带，得到了经纬同深度色织物的纱线颜色与织物颜色的对应，建立了经纬同深度的色织物颜色预测模型，如下式所示：

（K/S）同深度色织物=0.922 1×[0.5（（K/S）经纱+（K/S）纬纱）]（4）

根据这一模型，由纱线的K/S值可推测出用该纱线织成的色织物的K/S值。

对于织物组织结构为经纬密相同的一穿一空平纹织物（1︰1），经纱和纬纱各占织物表面50%，若不考虑织物组织结构的影响，经纬同深度色织物的K/S值应与经纱和纬纱K/S值平均值相同，即织物的K/S值与纱线的K/S值关系应为图4中斜率为1的黑色直线关系。但是实际测量发现，织物的K/S值低于纱线的K/S值。从预测模型可知，纱线的K/S值乘以系数0.922 1才是对应织物的K/S值，即织物的K/S值降低了779%。因此，根据此预测模型可得出，对于本文采用的织物组织结构，同深度色纱织成织物的过程中，由于组织结构的影响，织物的K/S值降低7.79%。分析认为主要原因是在色纱交织成织物的过程中，由于纱线的屈曲形态发生改变，纱线与用其织成织物的表面状态不一致，对光的反射、吸收情况产生了变化。

2.2 经纬异深度纱线与其织物的颜色深度关系

2.2.1 经纬异深度纱线与其织物的K/S值曲线关系

为探究经纬异深度色织物与其经纬色纱及同深度的色织物（简称“目标色织物”）颜色深度关系，测试了不同深度的经纬色纱及其织物的K/S值曲线，并与目标色织物进行对比。以经纱和纬纱染色深度分别为3%和2%的色纱为例，探究了经纱和纬纱及其织成的异深度色织物（织物3），以及经纬纱线染色质量分数均为2%的目标色织物（织物1）和均为3%的目标色织物（织物2）的K/S曲线关系，结果如图5所示。

由图5可以看出，异深度色纱与其织成的色织物及目标色织物的K/S值曲线形状一致，最大吸收强度的位置不变，最大吸收强度的高度存在一定差异。说明同色相异深度色纱交织后，色相没有变化且与目标织物色相一致，但颜色深度存在较为明显的差异。试验发现，三只染料其他染色质量分数下的色纱及其织物的K/S值曲线关系与本例一致。

2.2.2 异深度纱线与其织物的K/S值的关系

根据异深度色纱与其织物K/S值曲线的关系，同样选用最大吸收波长处的K/S值为异深度色纱织成织物过程中颜色深度变化的衡量指标，探究经纱K/S值不变时，经纬异深度色织物的K/S值随纬纱的K/S值的变化情况，并进行拟合，结果如图6所示。

由图6可看出，当控制经纱K/S值不变时，经纬异深度色织物的K/S值随其纬纱K/S值呈线性变化。拟合系数较高（除了一个0.989 0的外，其余都大于0.990 0），说明它们具有良好的线性关系。由此可以判断，经纬异深度色织物颜色深度具有可控性及可预测性，即可以通过控制纱线中部分组分颜色深度不变，调整其他组分颜色深度以获得目标颜色深度的色织物。

从图6还可以看出，拟合直线的斜率不一致，说明当控制经纱K/S值不变时，色织物的K/S值随纬纱K/S值变化的规律是不一致的。这一现象也说明色织物的颜色深度不仅受到织物组织结构的影响，还受到经纬纱线颜色深度差异即经纬色纱同色性指数的影响。

2.3 经纬异深度的色织物颜色预测

2.3.1 经纬异深度的色织物颜色预测模型

色织物的颜色深度同时受到织物组织结构和经纬纱线颜色深度差异的影响，本文设计的经纬异深度织物具有与同深度织物相同的组织结构，因此织物组织结构对织物颜色深度的影响是确定的。若仅考虑织物组织结构的影响，对于1︰1平纹经纬异深度色织物的颜色深度预测模型，应为下式所示：

（K/S）异深度色织物=0.922 1×[0.5（（K/S）经纱+（K/S）纬纱）]（5）

按该预测模型得到的预测K/S值与实际测得的K/S值进行对比，通过预测偏差来衡量此预测模型的可靠性，并探究预测偏差与经纬色纱同色性指数的关系，以判断此预测模型的适用范围，结果如图7所示。

从图7可以看出，散点图的走势是向上的，说明预测偏差随着同色性指数的增大呈增加趨势。当同色性指数较小时，预测偏差也较小，表明当经纬颜色深度差异较小时，预测模型具有较好的预测精度，可以认为此时影响经纬异深度色织物颜色深度的主要因素为织物组织结构。

2.3.2 同色性指数临界值

为了确定所建立经纬异深度色织物与经纬同深度色织物预测模型的适用范围，预测偏差和同色性指数的关系（图7）可被一条水平线（指定的预测偏差）和一条垂直线（K=KC，KC为待定的临界同色性指数）分为A1—A4四个部分，可以认为A1和A4中的点属于错误预测点[12]。KC从小到大移动，当错误预测点最少时，认为此时的K值为预测偏差小于特定预测偏差的临界下限值;KC从大到小移动，当错误预测点最少时，认为此时的K值为预测偏差小于特定预测偏差的临界上限值;临界下限值和上限值的平均值定义为预测偏差小于特定预测偏差时的同色性指数临界值。预测模型的准确性用测试方法1.3.5中的式（3）计算。表2为预测偏差分别在2%和4%以下的同色性指数临界值及对应的模型准确率。

由图7和表2可知，当预测偏差要求在2%以内时，同色性指数临界值为1.23，模型准确率为85.53%。根据已有的对色织物颜色预测模型研究[13]，认为该预测模型具有良好的预测精度和预测准确率。由于经纱和纬纱对织物的贡献是一致的，同色性指数在1以下的临界值可以为1以上的倒数（1/1.23），即同色性指数的范围为0.81～1.23。由式（4）和式（5）可知，经纬纱线颜色深度差异在以上同色性指数范围内的异深度色织物与同深度色织物具有相同的预测模，当要求预测偏差小于2%时，预测准确率为85.53%。同理，预测偏差要求在4%或其他值以内，也可得到相关的预测信息。可以认为，对于与本文采用的织物具有相同组织结构的织物，根据对预测模型偏差的要求，可确定同色性指数范围，颜色深度差异在此范围内经纬纱线织成的异深度色织物可达到与同深度色织物相同的均一的表观颜色。所以，原色织厂定义为颜色深度不合格的色纱只要符合同色性指数范围规定是可以被重新使用的，这能降低色纱废弃量，有效节约生产成本。

3 结 论

本文以表观色深为衡量指标，建立了经纬同深度、异深度色织物颜色预测模型，并确定了异深度色织物与同深度色织物具有相同的、均一的表观颜色时，异深度色织物的经纬纱线颜色深度波动范围，有利于废纱重新使用，节约成本。

1）同染料同深度色纱交织成织物时，由于织物组织结构的影响，织物色深与纱线色深不同。以K/S值为衡量指标，建立经纬同深度色织物颜色预测模型，预测模型具有较高准确性;根据模型判断，织物的K/S值相较于纱线会下降。

2）同染料异深度色纱织成织物时，织物的色深同时受到织物组织结构和经纬颜色深度差异的影响。在一定的经纬纱线同色性指数范围内，可以仅考虑织物组织结构影响，建立经纬异深度色织物颜色预测模型。

3）经纬纱线的同色性指数在0.81～1.23时，异深度色织物与同深度色织物具有相同的预测模型，当要求预测偏差2%时，准确率可达85.53%，此时异深度色纱交织织物能与同深度色纱交织织物颜色一致。

4）根据对预测模型偏差的要求，可以确定同色性指数范围，颜色深度差异在此范围内经纬纱线织成的异深度色织物可达到与同深度色织物相同的均一的表观颜色。所以，颜色深度不合格的色纱只要在同色性指数范围内是可被重新使用，能减少色纱的废弃，节约成本。

参考文献：

[1]张迎晨， 张青松， 吴红艳， 等. 一种面料经纬纱互相遮蔽空白段长度获得方法及其应用： CN108265373A[P]. 2018-07-10.

ZHANG Yingchen， ZHANG Qingsong， WU Hongyan. A method for obtaining the blank length of fabric covered by warp and weft yarns and its application： CN108265373A[P]. 2018-07-10.

[2]蔡永东. 全棉紧密纱色织物的生产技术[J]. 上海纺织科技， 2007， 35（4）： 22-23.

CAI Yongdong. Production technology of dyed yarn fabric made of pure cotton compact yarn[J]. Shanghai Textile Science & Technology， 2007， 35（4）： 22-23.

[3]李竹君. 色织物的生产及工艺[J]. 纺织导报， 2010， 28（12）： 15-19.

LI Zhujun. The production and techniques of yarn-dyed fabrics[J]. China Textile Leader， 2010， 28（12）： 15-19.

[4]KARST D， YANG Y Q， BOYTER H， et al. Improved flow uniformity of dye liquor using non-uniform package density profiles[J]. Aatcc Review， 2004， 4（3）： 31-34.

[5]钱旺灿. 纯棉筒子纱染色[J]. 印染， 2013， 39（16）： 27-29.

QIAN Wangcan. Cheese dyeing of pure cotton[J]. China Dyeing and Finishing， 2013， 39（16）： 27-29.

[6]王保明， 黄雪红. 筒子纱染色工艺探讨[J]. 针织工业， 2005， 32（7）： 42-43.

WANG Baoming， HUANG Xuehong. A research on the cheese dyeing technology[J]. Knitting Industries， 2005， 32（7）： 42-43.

[7]吴建中. 浅析筒子纱染色的加工原理和调色质量控制原理[J]. 中国石油和化工标准与质量， 2017， 37（20）： 17-19.

WU Jianzhong. Analysis on the processing principle of cheese dyeing and the principle of color mixing quality control[J]. China Petroleum and Chemical Standard and Quality， 2017， 37（20）： 17-19.

[8]周秋宝， 陈君莉， 沈一峰. 蚕丝织物组织结构对其表观颜色深度的影响[J]. 实验室研究与探索， 2010， 29（6）： 40-44.

ZHOU Qiubao， CHEN Junli， SHEN Yifeng， et al. The influence of the organizational structure on the apparent color depth of silk fabric[J]. Laboratory Research and Exploration， 2010， 29（6）： 40-44.

[9]李昌垒， 马君志， 秦翠梅， 等. 有色黏胶纤维、纱线、织物间颜色规律研究[J]. 针织工业， 2016， 43（11）： 47-51.

LI Changlei， MA Junzhi， QIN Cuimei， et al. Study of color rules between colored viscose fiber and its yarns and fabrics[J]. Knitting Industry， 2016， 43（11）： 47-51.

[10]MOUSSA A， DUPONT D， STEEN D， et al. Colour change as a result of textile transformations[J]. Coloration Technology， 2008， 124（4）： 234-242.

[11]高瓊琼. 羊毛/锦纶混纺织物的同色性及上染速率的量化控制[D]. 上海： 东华大学， 2017.

GAO Qiongqiong. Controls of Color Consistency and Exhausting Rate for Wool/Nylon Blend Fabrics Dyeing with Acid Dyes in One-Bath[D]. Shanghai： Donghua University， 2017.

[12]LUO M R， MINCHEW C， KENYON P， et al. Verification of CIEDE2000 using industrial data[C]// AIC 2004 Interim Meeting. 2004.

[13]李启正， 朱炜婧， 金肖克， 等. 原液着色涤纶交织混色织物的颜色预测模型[J]. 纺织学报， 2017， 38（7）： 56-62.

LI Qizheng， ZHU Weijing， JIN Xiaoke， et al. Model for predicting color mixing of dope-dyed polyester interwoven fabrics[J]. Journal of Textile Research， 2017， 38（7）： 56-62.