改进无线网络控制系统状态估计方法与仿真

摘  要：在无线网络控制系统传统模型状态估计问题研究的基础上，对系统模型进行改进。在系统传感器与估计器之间建立多条通信信道，应用基于隐马尔可夫模型的标准卡尔曼滤波算法，模拟仿真多通信信道高效切换，分析在所述改进模型下，系统矩阵特征值与滤波器估计误差协方差矩阵敛散性之间的关系。MATLAB仿真实验结果验证了所述改进方法的合理性和可行性，具有一定的理论和实际意义。

关键词：无线网络控制系统;状态估计;卡尔曼滤波;数据包丢失;仿真

中图分类号：TP393.0     文献标识码：A

Improved State Estimation Method and Simulation of

Wireless Network Control System

LI Zihao

（School of Information Science and Technology， Zhejiang Sci-Tech University， Hangzhou 310018， China）

P1umH0@163.com

Abstract： This paper proposes to improve wireless network control system model based on research on the state estimation problem of the traditional model. Multiple communication channels between the system sensor and the estimator are established and standard Kalman filter algorithm based on the hidden Markov model is applied. Then， the efficient switching of multiple communication channels is simulated and relationship between system matrix eigenvalues and the convergence-and-divergence of filter estimation error covariance matrix under the improved model is analyzed. Results of MATLAB （Matrix & Laboratory） simulation experiment verify that the improved method proposed in this paper is rational and feasible， and has certain theoretical and practical significance.

Keywords： wireless network control system; state estimation; Kalman filter; packet loss; simulation

1   引言（Introduction）

随着通信技术、自动控制技术和计算机网络技术等学科技术的相互融合与渗透，利用一定形式的通信网络代替传统控制系统中“点对点”式的专线结构来连接被控对象、传感器、估计器、控制器和执行器等多个节点的网络控制系统（Networked Control Systems， NCSs）应运而生[1]。NCSs具有信息资源共享、系统布线简单、易于扩展和维护、增加系统灵活性和可靠性等优点，在自动控制领域和工业生产行业得到越来越多的研究与应用[2-4]。

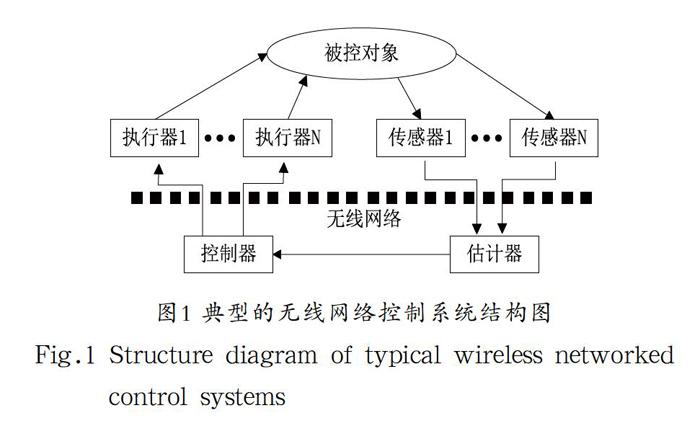
近几十年来，随着无线通信技术的飞速发展，无线网络控制系统（Wireless NCSs， WNCSs）逐渐成为新的研究对象。典型的WNCSs结构如图1所示。

2  WNCSs的优缺点及研究内容（Advantages， disadvantages and research content of WNCSs）

WNCSs在继承和增强NCSs优点的基础上，还具备成本低、系统部署安装和维护方便以及移动性和拓展性更强等优势[5-6]，因而被广泛应用于工业自动化、航空航天以及远程控制等领域。

虽然WNCSs具有很多优点，但是由于引入了无线通信网络，许多新的问题随之产生。在WNCSs中，所有的通信设备都是共享网络的，只有当共享的无线网络空闲时或设备的优先级相对较高时，待发送的信息才能发送出去，这就不可避免地会产生网络时延[7-8]。此外，在数据发送的过程中，受限于无线网络带宽，网络拥塞时有发生。还有，由于无线网络节点的可移动性强，连接中断、传输路径改变等现象也常发生，因此，WNCSs会发生数据丢包、数据包时序混乱等现象[9]。

在WNCSs中，随机时延与数据丢包是引起系统性能退化的主要原因。因此，对WNCSs的研究内容主要集中在如何减小随机时延和数据丢包对控制系统的影响[10-11]，从而保证无线网络传输的稳定可靠。

3   本文研究的問题（Questions studied in this paper）

针对WNCSs中随机丢包影响控制系统传输性能这一问题，一些学者在WNCSs传统模型状态估计问题上的研究已经取得了重要成果。文献[12]针对独立同分布的伯努利丢包下的卡尔曼滤波问题，从理论上证明了数据传输丢包率存在一个特定的临界概率，并给出其上、下界，当丢包率高于该值时状态估计器在期望意义上发散。文献[13]对马尔可夫丢包下的估计稳定性进行研究，提出了滤波器协方差峰值稳定的概念，并给出系统模型为向量情况下的卡尔曼滤波误差协方差峰值稳定以及一般意义下稳定的充分条件和标量情况下的充分必要条件。文献[14]将数据包到达过程建模成马尔可夫过程，设计了一种次优但效率高的估计器。

基于已有的研究成果，本文在WNCSs传统模型基础上进行改进，在系统传感器与估计器之间建立多条通信信道（如图2所示），应用基于隐马尔可夫模型的标准卡尔曼滤波算法，模拟仿真多通信信道高效切换，大幅降低丢包率，保证无线网络传输的稳定可靠。

4   问题描述（Problem description）

4.1   系统描述

本文对如下离散时间线性随机系统进行研究：

其中，代表系统矩阵，代表观测矩阵，和分别代表系统传感器的状态和量测，和是均值为零的高斯白噪声过程;是的协方差矩阵，是的协方差矩阵，且满足和，可控，可观;系统的初始状态是均值为零、协方差矩阵为的高斯随机向量，、和相互独立。

4.2   临界丢包率

数据包在不可靠信道的传输过程中存在丢失现象。直观上可以知道，数据丢包率越大，信息损失就越严重，滤波器估计误差协方差矩阵发散的可能性就越大。对于独立同分布的丢包过程，存在一个临界丢包率，使得只要信道平均丢包率小于该值，滤波器估计误差协方差矩阵收敛，估计误差协方差峰值稳定[15-16]。

利用MATLAB函数库，先求出系统矩阵的特征值：

然后再计算出系统矩阵的谱半径：

最后计算出临界丢包率：

其中，表示系统传感器与估计器之间建立的通信信道的数目。

5   卡尔曼滤波分析（Kalman filter analysis）

本文以双信道模型进行说明，进而可推广扩展到多信道模型。

步骤1：连接被控对象与传感器，在传感器与估计器之间设置两条马尔可夫信道，并同时设置两条通信信道的参数相同。

步骤2：设置循环次数，初始化、、观测值和真实值。应用如下双信道切换策略进行卡尔曼滤波。

假设初始时两信道均不发生数据丢包，首先利用其中一条信道（信道1）进行数据传输，如果这条信道传输成功次后失败，则切换到另一条信道（信道2）传输，信道2再传输成功次后失败切换回信道1。对于单信道传输系统，在信道传输错误后系统开始产生误差，如果继续由该信道传输，则它的丢包率会大于临界值，容易使估计误差值以指数型增长。如果采用上述的双信道切换策略，则避免了估计误差值的指数型增长。类似地，可以推广扩展到本文所述的无线网络控制系统改进模型，即传感器与估计器建立两条以上通信信道的传输系统，顺序检测通信信道的传输能力并评判其可靠性，按照合理高效、根据性能优先级排序的策略选择下一时刻的传输信道。

标准卡尔曼滤波方程为：

其中，为估计器的估计值，为估计误差协方差矩阵。循环完成后，计算得到的极限值。

步骤3：根据步骤2所述，计算循环中的估计值和估计误差协方差矩阵及其极限值，生成单信道与双信道传输系统状态估计性能比较图。

双信道传输系统状态估计问题研究仿真流程如图3所示。

6   仿真分析（Simulation analysis）

6.1   单信道与双信道传输系统状态估计性能比较

设置系统矩阵，观测矩阵，系

统协方差矩阵，观测协方差矩阵;设置循环次数为1，000，取0至1的随机数作为估计值、估计误差协方差矩阵和真实值的初始值，定义初始观测值，真实值第二列为;设置信道参数为。

仿真结果及分析：图4表明，在设置系统参数以及信道参数相同的情况下，单信道传输系统在某些时刻对系统状态真实值的估计存在偏差，而双信道传输系统则弥补了单信道传输系统在这些时刻的估计偏差，具有一定的可靠性优化效果。

图5表明，在设置系统参数以及信道参数相同的情况下，单信道传输系统在选定的时间范围内，仿真实验结果反映出其估计误差远大于双信道传输系统对这项指标的实验估计。

图6表明，在设置系统参数以及信道参数相同的情况下，单信道传输系统对于整个实验仿真期，仿真实验结果反映出其平均估计误差远大于双信道传输系统对这项指标的实验估计。

综合图5和图6，仿真实验结果对比反映出双信道传输系统相对于单信道传输系统具有更好的稳定性和可靠性。

图7表明，在设置系统参数以及信道参数相同的情况下，相对于单信道传输系统，双信道传输系统在传输丢包率这一直接反映传输系统稳定性和可靠性的指标上，较于前者减小将近一倍，具有很好的优化效果。这验证了本文提出的针对传统WNCSs模型的改进方法所具有的优势，具有一定的理论和实际意义。

6.2   单信道与双信道传输系统估计误差协方差矩阵敛散性分析

设置系统矩阵、观测矩阵、系统协方差矩阵和观测协方差矩阵等参数同6.1各项参数，以如下策略设置信道参数。

数据包在马尔可夫信道中成功传输概率，恢复概率。以此通过二次迭代设置信道参数，分析信道平均丢包率与临界丢包率的大小关系对传输系统估计误差协方差矩阵敛散性的影响，进而分析系统矩阵特征值与滤波器估计误差协方差矩阵敛散性之间的关系。

图8表明，无论是单信道还是双信道传输系统，当信道平均丢包率明显大于由系统矩阵计算得来的临界丢包率时，系統估计误差协方差矩阵的极限值趋于无穷大，矩阵发散;当信道平均丢包率逐渐向临界丢包率靠近时，系统估计误差协方差矩阵的极限值快速减小，矩阵发散程度减弱;当信道平均丢包率小于临界丢包率时，系统估计误差协方差矩阵的极限值趋于无穷小，矩阵收敛，表明此时传输系统数据包传输状况较好，有较高的稳定性和可靠性。

7   结论（Conclusion）

本文对所述改进无线网络控制系统状态估计的方法进行MATLAB仿真实验。实验结果表明，改进的多信道传输系统估计误差和平均估计误差值显著降低，丢包率大幅减小，说明该改进方法能够保证无线网络传输的稳定可靠。最后分析了在本文所述改进模型下，系统矩阵特征值与滤波器估计误差协方差矩阵敛散性之间的关系，具有一定的理论和实际意义。

本文从仿真实验结果中分析了改进的多信道传输系统的系统矩阵特征值与滤波器估计误差协方差矩阵敛散性之间的关系，得到只有当信道平均丢包率小于由系统矩陣计算得来的临界丢包率时，系统估计误差协方差矩阵才会收敛的结论，该临界丢包率符合临界丢包或临界稳定的条件。在计算临界丢包率的过程中，系统估计误差协方差矩阵的收敛性与系统矩阵的特征值相关，满足当的谱半径的次方（表示传感器与估计器之间建立的通信信道的数目）小于信道平均丢包率的倒数时，系统估计误差协方差矩阵收敛，这是从单信道至多信道的推广，具有一定的理论意义。

然而，本文所得推广结论尚未拥有详尽的理论推导和证明过程，但是它可以指出一个思考和研究的方向，我们期待更多的相关研究人员可以沿着该方向进行深入探究，通过严谨的理论推导过程得到更加准确的结论，这对于通信领域和自动控制领域来说都是十分重要的贡献。

参考文献（References）

[1] RAY A， HALEVI Y. Integrated communication and control systems： Part II-Design considerations[J]. ASME Journal of Dynamic Systems， Measurement， and Control， 1998， 110（4）：374-381.

[2] GRAHAM S， BALIGA G， KUMAR P R. Abstractions， architecture， mechanisms， and a middleware for networked control[J]. IEEE Transactions Automatic Control， 2009， 54（7）：1490-1503.

[3] 关守平，周玮，尤富强.网络控制系统与应用[M].北京：电子工业出版社，2008：22-34.

[4] YANG T C. Networked control systems： A brief survey[J]. IEEE Proceedings-Control Theory and Applications， 2006， 153（4）：403-412.

[5] HUA C C， ZHENG Y， GUAN X P. Modeling and control for wireless networked control system[J]. International Journal of Automation and Computing， 2011， 3（8）：57-363.

[6] 肖力.基于无线通信网络的估计与控制[D].武汉：华中科技大学，2009.

[7] PARK B， NAH J， CHOI J Y， et al. Robust wireless sensor and actuator networks for networked control systems[J]. Sensors， 2019， 19（7）：2-26.

[8] 刘义才，刘斌，张永，等.具有双边随机时延和丢包的网络控制系统稳定性分析[J].控制与决策，2017（9）：92-97.

[9] HUANG S， CHEN Z J， WEI C， et al. Stability analysis of networked control systems[D]. Cleveland： Case Western Reserve University， 2001.

[10] 陈雅雯.基于卡尔曼滤波的多控制器最优状态估计策略方法研究[D].北京：北京工业大学，2018.

[11] COOK J A， KOLMANOVSKY I V， MCNAMARA D， et al. Control， computing and communications： Technologies for the twenty-first century model T[J]. Proceedings of the IEEE， 2007， 95（2）：334-355.

[12] SINOPOLI B， SCHENATO L， FRANCESCHETTI M， et al.

Kalman filtering with intermittent observations[J]. IEEE Transactions on Automatic Control， 2004， 49（9）：1453-1464.

[13] HUANG M， DEY S. Stability of Kalman filtering with Markovian packet losses[J]. Automatica， 2007， 43（4）：598-607.

[14] SMITH S， SEILER P. Estimation with lossy measurements： Jump estimators for jump systems[J]. IEEE Transactions on Automatic Control， 2003， 48（12）：1453-1464.

[15] 黄俊华.无线网络化控制系统的协同控制与分布式一致性研究[D].广州：华南理工大学，2019.

[16] 谢承翰.事件驱动下无线网络化控制系统的状态估计和反馈控制研究[D].无锡：江南大学，2018.

作者简介：

李子豪（2000-），男，本科生.研究领域：无线网络控制系统，智能制造.