孤立波对礁坪上直墙冲击试验和RANS数值模拟

肖 理，房克照，孙家文，2，范子初，刘忠波

(1. 大连理工大学 海岸和近海工程国家重点实验室，DUT-UWA海洋工程联合研究中心，辽宁 大连 116024； 2. 国家海洋环境监测中心，辽宁 大连 116023； 3. 国家海洋局秦皇岛海洋环境监测中心站，河北 秦皇岛 066002； 4. 大连海事大学 交通运输工程学院，辽宁 大连 116026)

典型的珊瑚礁海岸由连接海床且较陡的礁前斜坡、延伸向岸滩的相对水平的礁坪组成，在礁前斜坡与礁坪相接处常存在隆起的礁冠[1]。岛礁地形的存在，会引起水深的急剧变化，导致波浪在岛礁上传播时发生反射、折绕射、破碎和波能衰减等现象。这些变化后的波浪是近岸结构物的主要荷载，对水工建筑、军事活动、港口和岛礁建设都具有十分显著的影响[2]。因此波浪在岛礁地形上的传播规律已成为海岸动力学研究的热点。由于风暴潮、海啸等海洋极端天气引起的极端波浪事件是工程界最为重视的海洋水动力因素之一[1]。而岛礁地形对波能衰减作用显著，绝大部分的波浪在珊瑚礁上破碎并在礁坪上传播时被耗散[3]，因此研究极端波浪下岛礁附近波浪作用的水动力过程对于海洋防害减灾具有重要的意义。由于在水动力方面存在相似性，孤立波一直被简化用来研究海啸波和岛礁的相互作用问题[4]。

在物理试验方面，Rober[5]早在2010年开展了孤立波在岛礁地形上传播的二维、三维水槽试验，这些数据被广泛用于数值模型验证。Quiroga和Cheung[6]在试验过程中引入底摩擦，研究了底床粗糙度对孤立波在岛礁上传播过程的影响。姚宇等[7]开展了一系列模型试验，研究孤立波在不同岛礁地形上的传播变形和爬高过程，从入射波高、有无礁冠、潟湖长度和底床粗糙度等角度全方面展开了探讨。这些研究基本集中在岛礁剖面上水动力特征，对于孤立波对礁坪构上筑物冲击的物理模型试验较少。在数值模拟计算方面，通常采用浅水方程模型、非静压模型、Boussinesq模型以及CFD类模型进行[3]。Berger等[8]、Stefanakis等[9]、任智源等[10]利用非线性浅水方程研究了海啸波与近岸岛礁的相互作用，但非线性浅水方程基于静压假设推导，不能考虑波浪传播演化过程中的色散效应。非静压模型考虑了动压效应，可弥补这一不足。陈同庆和张庆河[11]利用改进后的SUNTANS三维非静压模型，对南海东北部海域内孤立波进行模拟；张其一等[12]运用SWASH 模拟了典型珊瑚礁地形上的波浪传播过程，展示了非静压模型在珊瑚礁地形上良好的适用性。Boussinesq模型兼具色散性和非线性，可以较准确地模拟孤立波在岛礁地形上的传播过程。Roeber和Cheung[13]以及刘雨诗等[14]采用基于激波捕捉的Boussinesq方程成功地模拟了波浪在岛礁上的传播变形问题；孙志林等[15]利用Funwave-TVD模型准确地模拟了孤立波在岸礁地形的传播和爬坡；房克照等[16]建立了具有间断捕捉能力的 Boussinesq类波浪模型，并且用于模拟孤立波在岛礁地形上的传播，对比结果进一步表明了此类数值模型的精确度和适用性。但以上数值方法都不能有效模拟波浪破碎、相应的流场细节及波浪与构筑物相互作用，为克服这一缺陷，近年来一些学者通过采用CFD方法开展相关数值研究。高睿等[17]采用光滑粒子流体动力学(SPH)方法，研究了孤立波在斜坡地形上的传播、变形和破碎过程。姚宇等[18]采用大涡模拟的方法(LES)成功地模拟了孤立波在珊瑚礁礁前斜坡上的浅化、礁冠附近的破碎以及破碎波在礁坪上的演化过程。

文中将利用水槽物理模型试验和RANS数值模拟，研究典型岛礁剖面上孤立波的传播演化及其与礁坪后方直墙的相互作用过程。

1 试验布置

1.1 水槽布置

试验在大波流水槽中进行，水槽尺寸为69 m×2 m×1.8 m(长×宽×深)，图1是试验波浪水槽的布置图。水槽侧壁是玻璃，便于用相机记录和直接观察波浪传播演变过程。用Goring[19]提出的造波方法，在水槽的一端用推板造波机产生孤立波。岛礁剖面高0.4 m，前坡陡峭，坡度为1∶4，礁坪长6 m。坡面和礁坪表面由光滑的PVC板制成；在礁坪的末端安装高0.6 m的直墙。礁体模型距造波机推板平衡位置38.89 m，由钢架牢固支撑。礁冠也是由光滑的有机玻璃制成，可拆卸，高0.083 m，长1.55 m，两侧的坡度均为1∶4，安装礁冠后形成较长的前礁坡，礁后斜坡形成潟湖。对于这两种岛礁地形，礁坪上最小水深为0.093 m，礁冠上最小水深为0.01 m。在试验过程中，造波板处水深保持h=0.493 m恒定不变。以第四根浪高仪G4处测得的波高为入射波高(A=0.148 m)，无因次波高为ε=A/h=0.3，属于非线性较强的孤立波。试验重复三次，以获得可靠的数据。

1.2 测量仪器

试验一共采用33根浪高仪测量水槽沿程自由表面变化，它们的位置如图1所示。G1-G3用于校核造波信号，G4-G7位于模型海床前端，用于监测入射波和反射波。G8恰好位于斜坡脚趾上方(即x=38.89 m)。G7-G21间隔0.2 m，覆盖整个礁坡和部分礁坪，G21-G31间隔0.3 m，G32位于礁坪后方。最后一根浪高仪(G33)被放置在靠近垂直墙的位置，用来测量波浪爬高。四个ADV流速仪(声学多普勒测速仪)分别安置在x=39.81、40.91、42.69、44.04 m处。ADV的探头在礁面上方约0.04 m处。特别地，当地形安置礁冠时(x=40.49 m)，第二根速度传感器ADV2被移动到x=42.07 m处。采用15个沿直墙分布的微型压力传感器记录波浪对直墙的动态冲击荷载，每个传感器的直径均为0.004 m，间距为0.02 m；精确地安置在直墙竖向轴线上(图2是礁冠部分浪高仪布置图和压力测点分布图)。所有的仪器在试验前后都进行了校准，以确保线性和稳定性。自由表面、速度和压力荷载的数据采集频率分别为50 Hz、50 Hz和1 000 Hz。

图1 试验水槽和仪器布置示意Fig. 1 Layout of experimental flume and gague locations

图2 礁冠处浪高仪和直墙上压力传感器布置示意Fig. 2 Layout of wave gauge over reef crown and pressure transducers on vertical wall

2 数值模型

采用OpenFOAM中的Waves2Foam求解器进行数值模拟。Waves2Foam是一个可以产生和吸收自由表面水波的工具箱。能够产生孤立波、规则波、不规则波等各种波浪，该求解器的控制方程为连续方程和N-S方程，用VOF方法来追踪自由表面，有限体积法离散控制方程。

2.1 湍流模型

采用RANS k-ε模型进行数值模拟，k-ε模型求解了两个变量，k-湍流动能；ε-动能耗散率。OpenFOAM中标准的k-ε模型方程为：

(1)

(2)

k和ε的计算公式为：

(3)

其中，u是平均流速；I为湍流强度，I=0.16×Re-0.125；l为湍流尺度，一般取特征尺度的0.07倍，即l=0.07L；其余各常数取值分别为σk=1.00，σε=1.30，Cε1=1.44，Cε2=1.92，Cμ=0.09。

2.2 参数设置

理想化的数值波浪水槽应与物理水槽尺寸相同。但在实际模拟过程中，为节省计算资源和时间，下文只对物理岛礁地形段进行了数值模拟，即从x=23.8 m到x=46.49 m，长度为22.6 m。由G4(x=29.13 m)记录的波信号作为边界入射波高。边界条件设置如下：速度边界条件在入口处设置成waveVelocity，顶部边界设置为InletOutlet类型，出口设置成fixedValue，压力在顶部设置为totalPressure，其余边界处设置为zeroGradient；湍动能和耗散率在入口处设置为zeroGradient，底部和出口处fixedValue，由于建立的是一个二维数值水槽，前后两个壁面条件设置为empty。

为确定网格尺寸，进行了敏感度分析。分别取方案一：Δx=0.02 m和Δy=0.008 m；方案二：Δx=0.01 m和Δy=0.004 m；方案三：Δx=0.005 m和Δy=0.002 5 m三组网格进行波面与网格尺度的敏感度分析，结果如图3，方案三峰值明显偏离试验值，前两组结果无明显差异，考虑便于对波浪破碎的捕捉，最终确定网格尺度为Δx=0.01 m和Δy=0.004 m，网格在礁坪上沿x方向设置成渐变加密的形式，渐变系数为0.8；即最后一个网格的长度是第一个网格的0.8倍，以便更好地捕捉礁坪上的波浪破碎和直壁所受的动压力。无礁冠网格示意图见图4，有礁冠时只在网格底部加入礁冠地形，无其他特殊处理。

图3 波面变化与网格尺寸的敏感度分析Fig. 3 Sensitivity of wavefront change with mesh size

图4 计算网格示意(礁坪上渐变加密)Fig. 4 Schematic diagram of computational grid (gradual refinement on the reef flat)

数值模型在40核的台式工作站(2×20核Intel(R)Xeon(R)E5-2673 v4@2.30 GHz)上运行，内存32 GB RAM。模拟时间约为4小时，残差精度控制在1×10-6阶以内。各项数值模型参数设置如下：水的密度和运动黏度分别为ρ=1 000 kg/m3，ν=10-6m2/s；空气的密度和运动黏度分别为ρ=1 kg/m3，ν=1.48×10-5m2/s。在礁冠顶端时雷诺数达最大(Re=dU/ν=11 000)。经计算给出了k-ε模型湍流动能k=2.94×10-6m2/s2和耗散率ε=1.27×10-7s-1。采用四边形结构化网格对计算域进行离散。数值模拟的总时长为17 s，Courant数设置为0.45。时间步长在计算过程中自动调整，以满足数值模拟过程的稳定性，其中最大时间步长设置为0.001 s。

3 数值结果分析

对比数值计算结果和试验测量结果，包括自由面高程演变、流速、直墙上的波浪爬升和冲击荷载。还分析了RANS k-ε模型计算得到的湍动能和涡量分布。数值计算结果和试验测量数据在时空上都是同步的，以便进行比较，以孤立波波峰达到x=25.89 m的时刻定义数值计算时间零点(t=0 s)。

3.1 孤立波演化特征

3.1.1 无礁冠地形

试验观测到入射波在斜坡前保持完好的波形，在礁坪前端发生卷破，能量耗散，波幅减小，破碎波卷入空气以湍涌的形式在礁坪上传播并冲击直墙，较大的流速使得直墙处产生极大的爬高，反射波浪二次破碎并以湍涌的形式向造波机方向传播。

图5(a)是特征时刻自由表面数值结果和试验结果的对比图。图6(a)是对应时刻的湍动能和涡量场的数值模拟结果。由图可见，孤立波传播到礁前斜坡位置处时，由于浅水变形作用，波峰变陡并且略显倾斜状态(t=5 .5 s)，波形保持良好；在礁坪上水深更浅，波陡进一步增大，波浪明显变形并开始发生卷破 (t=6.5 s)；产生的湍动能和涡量的量级大约是O(0.2 m2/s2)和O(15 s-1)。随后波浪破碎，卷入大量空气并以湍涌的形式向直墙传播(t=7.6 s)。局部产生的湍动能和涡量在波头处达最大值，并且通过涡旋向下后方进行传播。最终波浪冲击直墙并引起爬高(t=8.7 s)。最大湍动能和涡量在这一过程有所减小且分散分布，此时湍动能和涡量分布于大部分水底，之后在直墙前形成澭水，外海和礁坪上水位下降，直墙附近的水面有巨大抬升，形成反射波(t=9.3 s)，反射波二次破碎并形成湍涌向外海传播(t=10.4 s，10.9 s)，这一过程湍动能和涡量聚集而增大。当波浪传播到外海，礁坪上波面恢复平稳，水位下降，礁坪上产生持续的低频波浪。整个过程数值计算结果和试验结果吻合较好。

图5 特征时刻自由表面的数值结果和试验结果对比Fig. 5 Comparison of numerical results and experimental results of free surface

数值模拟观察到8.7 s前后在水槽末端底部存在一个三角形区域，域内湍动能和涡量为零，这是由于破碎的波浪在水表面，且速度更快，湍动能通过涡旋向下和向后传播，所以水中的湍动能和涡量分布要比水面的延迟出现(7.6 s)，另外在直墙和礁坪的阻隔下，使得水槽底部这部分水体所受扰动小，流速为零，形成静水域，这也和试验观察相吻合。

3.1.2 有礁冠地形

图5(b)是礁冠地形下特征时刻自由表面的数值结果和试验结果。图6(b)是对应时刻的湍动能和涡量场的数值模拟结果。礁冠延长了斜坡的长度，孤立波在礁前斜坡发生浅水变形的时间较无礁冠地形情况更长，且礁顶水深变浅。可以看到在礁冠顶端，波浪已经不具有稳定的波形，在礁冠末端卷破。此时湍动能几乎为零，但是涡量聚集在一个点且量级达到了O(20 s-1)。可以认为处于临界破碎状态(t=6.0 s)；破碎点和无礁冠地形相比明显提前。之后波浪传播到潟湖，形成水跃，波浪破碎后卷入大量空气并发展成湍涌在礁坪上传播(t=6.7 s，7.0 s)；这一时刻波头的湍动能最大值达到0.4 m2/s2，涡量最大值达到20 s-1。并通过涡旋向下向后传播，从图中可以看出涡量由聚集到分散的过程；随后波浪冲击直墙，湍动能和涡量急剧下降，分散于水底，在水槽末端存在一个静水三角域。这和无礁冠地形情况类似(t=9.0 s)。t=10.5 s波浪发生反射并且反射波保持良好的波形，产生的湍动能达0.3 m2/s2，涡量只有5 s-1。对比无礁冠地形反射波破碎的情况，说明礁冠的存在对潟湖区极端波浪的产生有一定抵制作用。之后反射波向外海传播，在礁顶和礁冠前坡均发生破碎(t=12.4 s，14.0 s)。

图6 特征时刻湍动能和涡量数值模拟结果Fig. 6 Numerical simulation results of turbulent kinetic energy and vorticity

值得注意的是在t=7.4 s时，礁冠背面斜坡处出现了湍动能和涡量的极值。波形呈朝来波方向的卷舌状，t=9 s波浪向来波方向破碎。从图7可以观察到，孤立波破碎后在礁坪上传播过程中，大部分湍涌朝直墙传播，与此同时礁冠背面产生一个反向的水流，部分波浪向来浪方向破碎并冲刷在礁冠背面，能量在礁冠背面耗散。这与姚宇等[20]试验测得珊瑚礁礁冠会产生反向水流结果类似。

图7 礁冠地形波浪传播过程试验照片Fig. 7 Snapshots of wave propagation process

3.2 波面和流速历时曲线

图8是无礁冠、有礁冠地形试验和数值模拟波面历时对比曲线。数值模拟能够准确模拟孤立波主要演化过程。主峰的数值模拟和试验结果取得较为精确的吻合，但在礁坪上，波形有破损(G26)。两种地形上，浪高仪测点在采集到礁坪上波浪和反射波浪时出现了不同程度的高频振荡，然而在数值模拟中这些细节被光滑的曲线替代(G22、G26)，这是由于波浪破碎后形成的湍涌包含许多细小的涡旋，这些涡旋会造成电压的扰动而在试验采集中被记录下来。而RANS模拟只能得到湍流平均物理量，捕捉不到这些小尺度涡旋。况且波浪破碎卷入空气后是一个具有随机性的过程，这对数值计算也是一个难点。另外，可以观察到无礁冠、有礁冠地形入射波的尾波和反射波的尾波都不同程度的偏离试验值，导致这一现象的可能原因是OpenFOAM数模造波和试验室推板造波存在差异。总体而言，RANS k-ε封闭湍流模型能对孤立波传播过程中自由表面进行较为准确的捕捉。

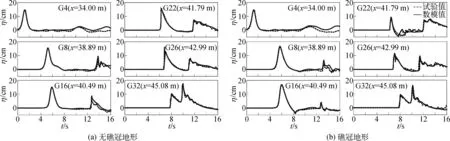
图8 自由表面时间历程对比曲线Fig. 8 Comparison of free surface time history

图9比较了4个流速仪的水平速度分量的时间历程。整个过程OpenFOAM都成功地捕捉到了波浪从外海传播到礁坪和反射后的流速分布。其中无礁冠地形数值模拟结果吻合程度比礁冠地形高。ADV1位于斜坡中部，记录礁前斜坡处波浪浅水变形过程中流速的变化，无礁冠地形下，波浪在坡前无反射，流速分布呈对称。加上礁冠后，前礁坡有明显的反射。流速下降到负值。ADV2位于礁坪前端，在无礁冠地形下，此时波浪变形但尚未破碎，流速分布不对称，由于礁冠的存在，礁冠地形下ADV2移至x=42.07 m处，由图5(b)和图6(b)(t=7.4 s)以及图7可知在礁冠背面产生反向的水流，与流速仪所测得的流速迅速降低到负值相吻合。而数模值没有捕捉到这一变化的可能原因是空气的混入影响到了数值模型的捕捉。ADV3以及ADV4数值模拟和试验采集具有整体趋势的相似性，但在细节上数值模拟并不能完全反映出来，这也可能是破碎波卷入空气导致模拟不准确。从图中可以看出，有礁冠地形下ADV3、ADV4所测的最大正向流速均小于无礁冠地形，这说明礁冠的存在使得礁坪上的流速减小。可能的原因有：礁冠的存在增大了孤立波的反射，同时改变了礁坪上的水深，且形成的反向水流在礁冠背面破碎，从而增强了孤立波破碎损耗的能量。

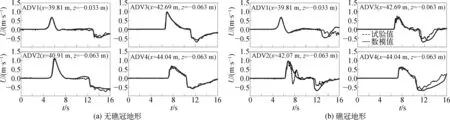
图9 流速时间历程曲线Fig. 9 Comparison of velocity time history

3.3 反射前沿程最大波面

图10是无礁冠、有礁冠地形反射前沿程最大波面的试验结果和数模结果对比图。从图中可以看出，无礁冠地形下波浪在礁前斜坡发生浅水变形，波面抬高却不至于破碎，随后最大波面有所降低，并在礁坪中部第二次抬高，波浪发生破碎，沿程最大波面变小；礁冠的存在使得波浪在礁冠处产生极大的抬高并破碎，之后整个过程沿程最大波面明显减小。有礁冠地形的破碎点较之无礁冠地形提前，能量释放更早，因此礁坪上传播的最大波面要小于无礁冠地形的波面，且试验记录波浪在无/有礁冠两种地形上反射时在直墙处的爬高分别为0.405 m 和0.347 m。礁冠的存在使得礁坪上的波浪变小，能大幅度减小波浪在直墙上的爬高，对潟湖、直墙起到一定的掩护作用。

图10 沿程最大波面Fig. 10 Maximum wave height along wave flume

3.4 直墙上压力分布

图11是无礁冠、有礁冠地形直墙所受压力的试验和数模值对比结果。两种地形下直墙所受冲击过程相似，从P1到P11测点，压力峰值先增大后衰减。整体而言，OpenFOAM对压力的捕捉都是比较成功的，但并未准确地捕捉到P6～P8测点处的最大瞬击荷载；从图中可以看出，数值结果明显小于试验结果。最大误差分别是45%(无礁冠地形P7测点)和54%(有礁冠地形P6测点)。分布在静水面和水面以下的测点(P1～P5)，压力先达到一个极值随后又增大到最大值，然后衰减。位于水面以上(P6～P9)测点，压力直接到达最大值，衰减后又增大到极值，之后衰减至零。这可能是波浪破碎冲击直墙的位置处于P6～P9测点之间而产生的巨大瞬击荷载，随后产生的澭水导致了第二个极值的产生。图12是所有测点最大压力值，从下至上，最大压力值有一个先增大后衰减的过程，结合G32测点测得的无/有礁冠地形湍涌最大高度为0.105/0.093 m，可知湍涌与直墙的作用位置分布在P5～P9区间。故在P6、P7、P8产生的瞬击荷载很大,最大值出现在P6(礁冠)或P7(无礁冠)测点处，礁冠地形测得最大瞬击荷载的测点位置要低一些，是因为礁冠的存在让礁坪上最大波面低于无礁冠地形，冲击的位置有所降低而导致的。对于试验结果和数值结果都有个共同特点，除个别点外，有礁冠地形下的每个测点的压力最大值都小于无礁冠地形下相应的测点。可以想象礁冠的存在，有助于减少直墙所受压力。

图11 压力历时曲线对比图Fig. 11 Comparison of pressure time history

RANS k-ε模型能够重现孤立波对直墙的冲击过程。整体来看，数值模型对直墙测点的压力变化有一个准确的描述，但当波浪破碎时，尤其是破碎和结构物共存时，在对瞬击荷载的捕捉时，RANS k-ε模型模拟的结果明显偏小。如图12(b)、(c)是波浪冲击直墙的瞬时照片和数值模拟的结果，可以看到冲击过程中，波浪破碎严重且夹杂着大量的空气，实际测量中瞬间的电压变化可以被仪器记录下来，但要在数值模拟中重现这一过程就显得相当复杂且不准确。传统的RANS模型只计算平均运动，而波浪破碎形成的细小涡旋且混入大量空气，这是传统的RANS模型无法处理的。对此，许多学者通过改进传统的湍流模型来取得更高的精度，并结合试验数据得到了很好的拟合效果，Brecht等[21]改进的k-ω SST湍流模型能够准确捕捉孤立波的爬高；邹学锋等[22]结合传统湍流模型，提出适用于珊瑚礁地形的k-ω SST湍流模型；Eltard和Fuhrman[23]发现传统的湍流模型对湍动能预报偏高，改进并提出稳定多相流湍流模型(multiphase turbulence stabilization)。如果要得到更精准的数值模拟结果，可以提高网格质量并采用改进的湍流模型来进行数值模拟。

图12 直墙所受最大压力与试验和数模结果照片Fig. 12 Maximum pressure on vertical wall and snapshots of experiment and simulation

4 结 语

采用物理模型试验和数值模拟相结合的方式研究了孤立波在有礁冠和无礁冠的礁坪上的传播过程及其对礁坪上直墙的冲击作用。

对于文中的两种岛礁地形，发现入射孤立波都会在礁坪或礁冠上破碎，并发展成湍涌，在岸上传播，最终冲击直墙。结果表明，RANS k-ε模型能够准确再现孤立波的主要演化过程以及波浪与直墙的相互作用，特别是能直接观察到湍动能和涡量场的演变，这是试验所不能得到的。不足之处是不能准确捕捉直墙最大瞬击荷载，主要的一个影响因素是RANS不能捕捉破碎后的细小涡旋。且破碎的波浪卷入空气使得整个冲击过程具有很大的随机性。从试验数据和数模结果来看，由于礁冠的存在，波浪提前在礁顶破碎，礁坪上波高显著降低，释放能量较无礁冠地形更早；礁冠背面形成的反向水流对外海的来浪起到一定的阻挡作用，部分能量在礁冠背面释放，使得礁坪上流速减小，从而减小了直墙上的爬升和最大动压。所以礁冠的存在对近岸直墙、建筑物能起到一定的掩护作用。

当波浪破碎时，RANS k-ε模型模拟的结果显得不够精确，尤其是不能捕捉到瞬击荷载，波浪破碎的研究一直是难点和热点，传统的湍流模型在处理波浪的破碎过程稍显不足，为进一步研究孤立波与岛礁地形上建筑物的作用，物理模型方面需要增加更多的试验组次；数值模拟方面可以采用改进的湍流模型或者能够捕捉小尺度涡旋的大涡模拟(LES)方法。