深度学习在时空序列预测中的应用综述

刘 博，王明烁，李 永，陈洪丽，李建强

(北京工业大学信息学部，北京 100124)

目前，时空数据广泛存在诸多领域，如交通运输[1-2]、气候科学[3-4]、按需服务[5-6]、神经科学[7-8]等.由于这些领域所研究的内容在现实世界中本就存在固有时空特性，再加上近年来定位系统、传感器网络等技术的快速发展，物理存储能力不断提升，使得在现实中采集得到的时空序列数据呈爆炸式增长，所以准确挖掘以捕获海量时空序列数据中的时空特征，并在此基础上建模对时空序列预测至关重要.

时空序列数据是嵌入在连续空间中，同时具有空间和时间相关性的数据，可以通过不同角度定义时空序列以及时空序列的特征，可以将空间位置视为对象，并将随着时间推移从空间位置收集到的属性值来定义特征，也可以将时间点视为对象，考虑使用所有的空间位置收集到的属性值来定义特征.由于时空序列数据在时空维度存在相互依赖的关系，通常具有高度的自相关性.也正是时空序列数据的这些特点，使得经典数据挖掘技术直接应用在时空序列数据上性能较差，无法捕获其中复杂的时空数据相关性.

对时空序列预测时，不仅要考虑时间维度上的依赖性，同时还要考虑空间维度的依赖，而随着时间推进，空间维度的相关性也会发生动态变化[9].目前已有大量针对时空序列预测的研究工作，主要分为数值预报方法和统计预报方法.数值预报方法是依靠研究人员具有大量的先验知识和经验，从而建立预测模型.统计预报方法是基于数理统计的方法，在大量数据的基础之上，建立模型以找到输入变量和输出变量之间的关系.统计预报方法包括基于传统参数模型的时间序列预测方法、基于传统机器学习的时空序列预测方法和基于深度学习的时空序列预测方法.其中基于传统参数模型的预测方法难以捕获数据中的非线性特征，基于传统机器学习的时空序列预测方法可以自动捕获数据中的非线性特征，在小样本上具有很好的泛化能力.而基于深度学习的时空序列预测方法不仅可以有效挖掘数据中的有效信息，自动捕获隐藏的线性及非线性特征，还可以高效处理大规模时空序列数据.

虽然目前深度学习技术已广泛应用于时空序列预测任务，但仍存在诸多问题.首先对于时空序列数据本身而言，在时间维度存在大量缺失值、噪声，以及空间维度尺度不一致的问题，而现有的数据处理方法大多针对传统的关系数据，较少针对时空序列数据.其次对于深度学习模型的选择，目前缺乏如何根据不同的数据类型、数据实例以及数据格式选择对应的深度学习模型的研究和指导.最后就是针对深度学习模型的可解释性，由于数据和关系的复杂性，需要对最终的时空序列预测结果进行很好的解释，以方便理解.

1 时空序列数据

时空序列数据是对不同区域内随时间推移研究对象的变化过程的抽象表示.不同于传统的关系数据，其表示形式更为多样，处理方法较为复杂.时空序列数据存在时间维度上的顺序依赖，通常根据事先设定的采样频率，在相等的时间间隔内对所要研究的随机变量进行观测和记录，从而得到序列数据[10].

1.1 时空序列数据属性

时空序列数据的属性包括海量性、自相关性、异质性、高维性.

时空序列数据来源广泛、积累时间较长，导致时空序列数据量较大，而有效处理海量时空序列数据是时空序列预测的首要目标.

时空序列数据在时间维度和空间维度上具有相关性，即在时间戳上和空间位置上的观察不是相互独立，而是相互关联的，甚至这2个维度的观测结果具有一致性.由于时空序列数据存在这种自相关特性，在使用时空序列数据时，需要考虑传统预测方法的适用性.

时空序列数据在时间维度和空间维度上具有非平稳性，即以不同的方式显示出一定的异质性，导致不可以用同一个模型去概括不同时空区域的特征，需要学习不同时空区域下的不同模型.例如，由于季节性的存在，对空气质量的预测不可一概而论；由于一天中不同时段交通流量存在周期性以及存在动态变化的特征，因此应对多时段构建不同的预测模型.

由于时空序列数据除了具有时间维度特征和空间维度特征，还具有属性维度等多维特征，因此在时空序列预测时，可以借助时空维度之外的多维属性特征以捕获额外信息.如在空气质量预测中，影响空气质量的因素复杂且多样，除气象气候数据外，目标区域内工厂的数量也会对空气质量产生影响等.

在对时空序列进行预测时，需要充分考虑时空序列数据的属性特征，并做出相应处理，才能针对不同领域内实际的时空序列预测任务给出更加精准的预测结果.

1.2 时空序列数据类型

1.2.1 事件数据

事件数据通常可以用事件的类型、事件发生的位置以及事件发生的时间来表示，可以通过三元组(e,l,t)来描述，其中：e为事件的类型；l为事件发生的位置；t为事件发生的时间.时间序列数据的点事件的集合称为空间点模式[11].事件数据在犯罪学、流行病学、社交网络等领域被广泛应用.图1(a)在二维坐标中展示了2种事件数据，并使用不同的分类标记进行表示.

1.2.2 轨迹数据

轨迹数据是由部署在可移动物体上的位置传感器获得，传感器会定期记录并传输移动物体的位置信息，从而轨迹数据可以描述出随着时间的推移，物体在空间中的移动路径.轨迹数据可以用序列{(l1,t1),(l2,t2),…,(ln,tn)}表示，其中：l为位置信息；t为移动物体通过该位置的时间信息.轨迹数据在运输、生态应用中很常见.图1(b)展示了2个移动物体的2条不同的轨迹.

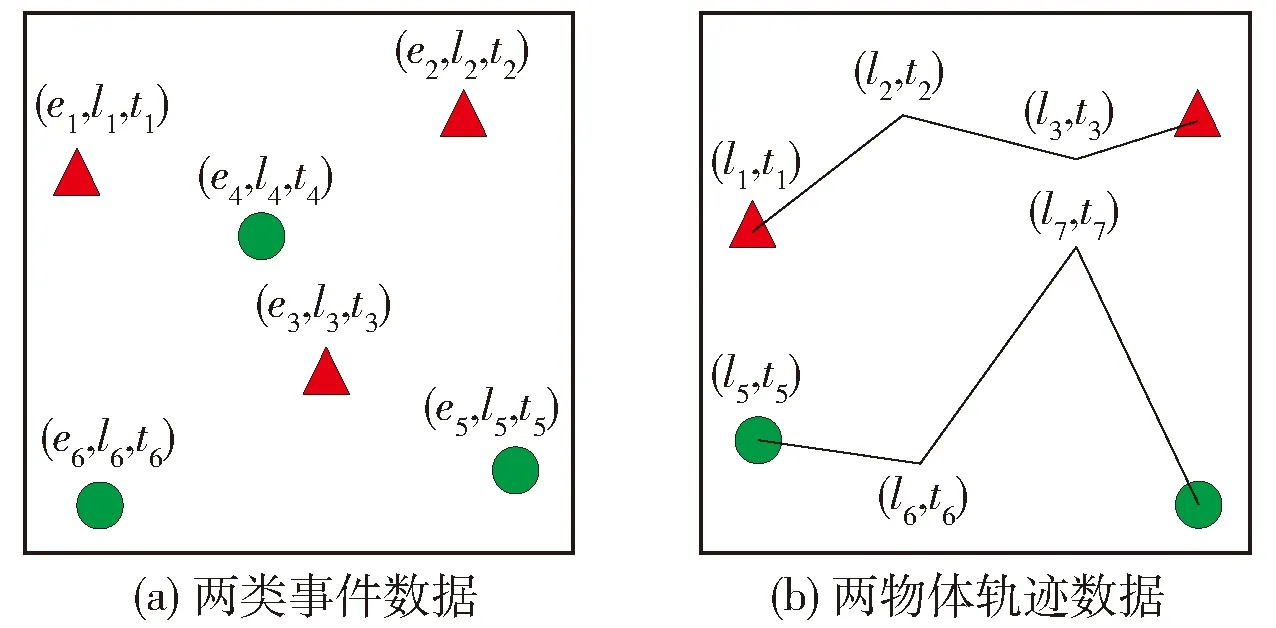
图1 事件数据和轨迹数据示例Fig.1 Illustration of event and trajectory data types

1.2.3 点参考数据

点参考数据在空间统计学中也称为地统计数据，是由一组在特定空间和时间间隔内移动的点参考而测量得到.值得注意的是，在点参考数据中，传感器的位置会随时间而发生变化.图2(a)(b)分别展示了相邻时间点的参考点数据的示例，其中图例表示空间中的测量分布.

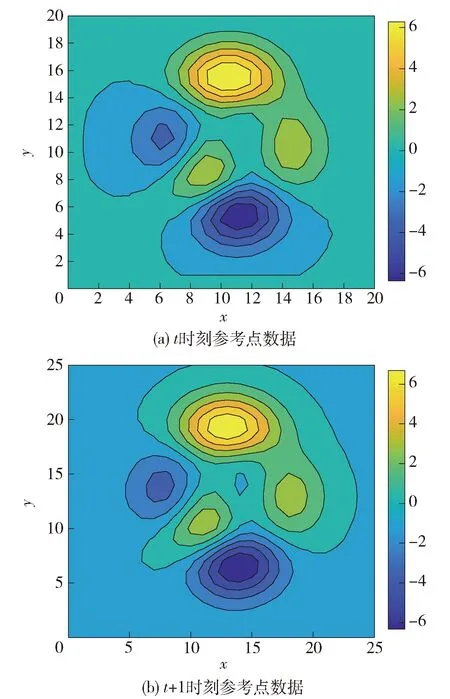
图2 点参考数据示例Fig.2 Illustration of point reference data type

1.2.4 栅格数据

栅格数据是在固定的空间位置、相等或不等的时间间隔下，通过记录连续或离散的测量值而得到的.与点参考数据不同的是，记录栅格数据的传感器的位置固定不变，而这些固定不变的位置要么规则地分布在空间中，如图像的像素，要么以不规则的空间模式分布，如用于监测空气质量的站点.栅格数据可以表示为：一组固定的位置S={s1,s2,…,sm}，以及在每个位置上的时间序列集合T={t1,t2,…,tn}.通常应用在交通学领域、气候科学领域、神经科学领域等.图3(a)(b)分别表示规则分布以及不规则分布下的栅格数据.

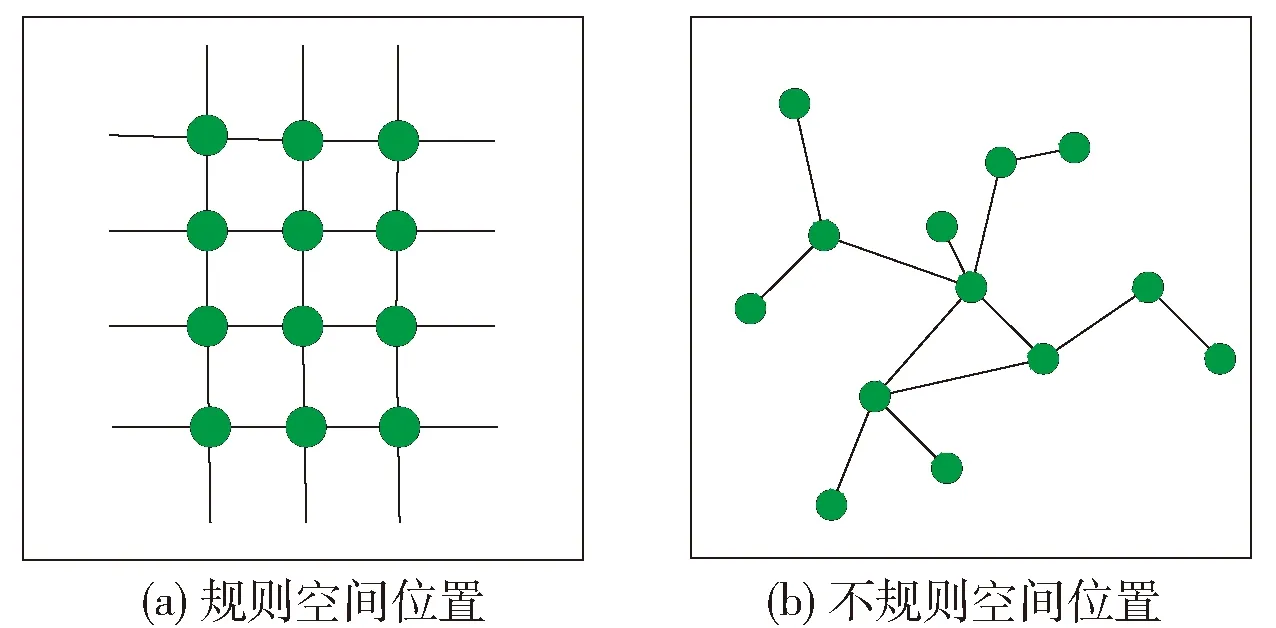
图3 栅格数据示例Fig.3 Illustration of raster data type

虽然收集到的时空序列数据呈现不同的数据类型，但在某些情况下，不同的数据类型间可以相互转化.通过将一种类型的时空序列数据变换成另一种时空序列数据类型，可以更方便地处理和计算.如可以采取某些特殊的事件提取算法将栅格数据转换为事件数据，此外点参考数据和栅格数据也可以相互转换，对点参考数据进行插值处理以转换成为栅格数据，将栅格数据的每个点视为参考点，也可以将栅格数据转化为点参考数据进行处理.

1.3 时空序列数据实例与表示

数据实例指用于数据挖掘以及机器学习的基本数据单元，如时间序列、轨迹等.时空序列数据类型不同，可以对应表述为不同的数据实例，即使对于相同的数据类型，也可以构建不同的数据实例以方便不同的任务.

时空序列数据有5种常见的数据实例，分别是点、轨迹、时间序列、空间图以及时空栅格，图4总结不同时空序列数据类型与不同的时空序列数据实例间的对应关系.

图4 不同数据类型的实例与表示Fig.4 Data instances and data formats of different data types

事件数据可以自然地表示为点实例，轨迹数据可以表示为点实例的集合、轨迹实例以及带有空间位置的时间序列实例，点参考数据由点实例组成，而栅格数据可以有3种实例表示的形式：第1种可表示为不同空间位置下的时间序列实例；第2种可表示某时刻下的一组不同空间位置的测量值，构成空间地图实例；第3种可将栅格数据看成一个整体，构建时空栅格数据实例.

可以根据不同时空序列数据类型构造不同数据实例，而正确构造实例的方法取决于所要研究的问题类型和性质.对于上述5种数据实例，提出5种对应的数据格式来表示用于深度学习模型的输入，如图4所示，分别是点、序列、图形、二维矩阵以及三维张量.点实例可以直接表示为点，还可以表示为二维矩阵，轨迹实例可以表示为序列以及二维矩阵，其中二维矩阵的2个维度分别是所在区域的行列坐标，时间序列数据则自然地表示为序列，空间地图可以表示为图形或二维矩阵，时空栅格数据实例可以用二维矩阵或三维张量表示，二维矩阵的2个维度分别是位置和时间戳，而三维张量则增加区域的行列信息.虽然二维矩阵的表示更加简单，但会一定程度丢失空间信息，降低时空序列预测的精度.不同的深度学习模型需要对应具有不同表示形式的输入数据.

2 时空序列预处理方法

时空序列数据目前存在的问题包括时间维度数据的缺失，即时间序列不完整、存在噪声干扰，以及空间维度数据尺度不一致，以上问题严重影响时空序列的数据质量，而针对时空序列数据的预处理方法便是通过有效的手段在一定程度上提高数据质量，为后续时空序列数据的挖掘、分析以及建模做准备.

2.1 时间序列缺失值估计

由于时空序列数据来源广泛，包括GPS、遥感卫星等传感设备采集的数据，调查数据，基础地理信息数据等，时空序列数据呈爆炸式增长.但在数据收集过程中，会由于数据的获取、存储，以及人为原因，导致最终数据集中存在一定的不完整性，可能是单个或多个属性的缺失，也可能是单条或多条记录的缺失，这些数据被称为缺失数据，在数据预处理步骤需要对缺失数据进行估计.

目前，对时间序列缺失值的估计方法主要包括统计学方法和机器学习方法.

其中统计学方法包括4种类型：1)记录删除法.该方法对数据集中存在缺失值的数据做删除处理，即只考虑并使用完整的记录进行分析.该方法实施较简单，但由于直接删除缺失数据，很有可能丢失重要信息，且不适用于存在大量缺失值的数据集.2)基于权重的方法.在数据产生的过程中，都有与之对应的权重信息，该方法在遇到缺失值时，对权重重新计算，但该方法存在数据丢失现象.3)替代法.该方法利用数据集中的某种统计值替代缺失值，替代法在处理缺失值中被广泛使用，如均值替代法等，但仍不适用于存在大量缺失值的数据集.4)基于模型的方法.该方法首先对缺失值的缺失机制进行判断，然后建立一定的模型，对缺失值进行估计.该方法应用较灵活，且可应用于缺失值较多的数据集，所以被广泛应用，常用方法包括期望最大化法、多重填补法、极大似然估计法等.

用于缺失值估计的机器学习方法包括K邻近法、BP神经网络等.其中K邻近法的基本思路是找出与缺失值距离最近的K个完整数据，然后使用这K个数据的均值来估计缺失数据.BP神经网络则利用已知完整数据训练神经网络，将完整数据作为网络的输入，缺失数据作为网络的输出，然后再将有缺失值记录中其他已知数据输入训练好的网络，网络的输出则是对缺失值的估计.

基于统计学的方法直接处理的是模型参数的估计，而并非缺失值本身，且模型在估计缺失值时收敛速度较慢.而且现实收集到的时间序列数据具有非线性、非平稳的特征，传统基于统计的模型不能很好对缺失值进行估计.随着机器学习的发展，其在时间序列数据缺失值的研究中不断涌现新的方法，一定程度上解决统计学方法不能处理非线性的问题，目前基于机器学习的缺失值估计方法被广泛应用.

2.2 时间序列去噪

时间序列数据获取过程中会因为观测误差、系统误差或其他原因，导致时间序列数据中存在一定的噪声，而噪声严重影响数据的处理结果，所以在数据预处理阶段，应根据噪声的类型，选用不同方法对数据进行去噪处理.

通常采用滤波的方法对时间序列数据进行去噪处理，分为时域滤波方法和频域滤波方法.

时域滤波方法通常使用滑动窗口作为滤波器，利用滑动窗口内的统计值来代替，从而达到分离信号和噪声数据的目的.常见的时域滤波方法包括均值滤波、中值滤波、自适应滤波等.其中前二者的滤波原理相同，使用固定大小的平滑窗口对噪声序列进行滑动处理，直至序列结束，使用滑动窗口内不同的统计值作为窗口中心的值.自适应滤波器则是通过对局部统计参数的调节达到对噪声数据平滑的目的.

频域滤波方法是将信号数据由时间域变换到频率域，通过设定适当的阈值，区分高低频信号，低频信号属于有效数据，高频信号属于噪声数据.传统的频域滤波方法主要包括卡尔曼滤波、维纳滤波、低通滤波等.维纳滤波是一种线性滤波方法，低通滤波可以很好地处理噪声数据，但对波动较大的时间序列数据不适用.随后还有小波方法在信号去噪的应用[12]，应用最广泛的是小波阈值去噪.

时域滤波方法适用于非平稳数据，速度快且处理结果比较平滑，但是不能保留数据局部细节的变化；空域滤波可以有效区分噪声数据，但易忽略数据中的突变信息，具有一定的局限性.

2.3 空间数据尺度转换

空间数据的尺度特性由空间分辨率来表示，但目前由于数据来源不同、获取数据的手段存在差异，导致空间数据尺度不一致.而对时空序列的挖掘以及处理需要在同一尺度下综合分析多要素空间数据之间的联系，所以需要在数据预处理阶段对空间数据尺度进行一定的转换.

现有尺度转换方法多是基于统计模型的方法，包括重采样法、地统计法、小波分析法等.

重采样法常用于栅格数据的尺度转换，广泛使用的方法是最邻近法、双线性法、立方卷积法等，分别适用于离散数据、连续数据以及遥感影像数据.地统计方法考虑变量的随机性和相关性，一定程度上提高了插值的精度，也便于误差分析.小波分析法则将空间位置信息与空间数据的尺度特性联系起来，可对多尺度地理信息进行融合.

基于统计模型的空间数据尺度转换方法较少考虑空间数据的结构信息，容易忽略空间相似性变异的情况.

3 时空序列预测方法

时空序列由多条空间相关的时间序列组合而成[13]，可以将长度为M的时间序列定义为时间矩阵

X1:M=[X1,X2,…,XM]

P={{S1,T1},{S2,T2},…,{Sp,Tp}}

式中：p为不同空间位置的数量；Si为第i个空间位置信息；Ti为对应空间位置下的历史时间序列，即上述时间矩阵X.

时空序列预测任务是根据不同空间位置的历史观测结果预测出长度为L的序列数据，即找到其中的映射关系，可表示为

XT+1：T+L=F(X1：XT)

时空序列预测分为单步和多步时空序列预测.当L=1时，属于单步预测，即仅根据历史时空序列数据预测下一时刻的观测值.当L>1时，属于多步预测，即根据历史时空序列数据预测接下来一段连续时间的观测值.多步时空序列预测方法分为间接和直接多步预测.间接多步预测方法通过预先训练好的单步预测器进行单步预测，并将预测结果作为样本输入到单步预测器进行下一步预测，由此，上一时刻的误差也会传到下一时刻，会导致误差不断积累，预测效果不佳.为了解决这一问题，提出直接多步时空序列预测方法，对于不同的时间间隔分别构建模型并训练，然后直接进行预测.

3.1 基于传统参数模型的时间序列预测方法

基于传统参数模型的预测方法主要针对于时间序列预测，几乎不考虑不同位置间的相互影响.利用传统参数模型进行预测首先需要确定即将采用的模型，并在此基础之上，求解出相应的参数，进而完成时间序列预测任务.表1总结基于参数模型的时间序列预测方法.

表1 基于参数模型的时间序列预测方法总结Table 1 Summary of time series forecasting methods based on parametric models

历史平均法(historical average，HA)是将同一观测位置下研究对象在相同时间间隔内的历史记录取算术平均值或加权平均值，作为下一时刻的趋势预测值，该方法是一种比较简单的时空序列预测方法，实施较方便，但预测精度有限.

自回归滑动平均模型(autoregressive moving average model，ARMA)又称“Box-Jenkins方法”，该方法建模的前提是所用时间序列由零均值稳定随机过程产生的，即ARMA仅可以处理稳定时间序列.特例差分自回归移动平均模型(autoregressive integrated moving average model，ARIMA)通过使用差分方法将非稳定时间序列转化为稳定时间序列进行处理.在ARIMA的基础之上，提出时空自回归差分移动平均模型(spatio-temporal autoregressive integrated moving average model，STARIMA)，在求解STARIMA模型的过程中分为模型识别、参数估计和模型验证三步迭代，其中模型识别涉及时空特征的学习，其根据时空自相关函数来确定模型的3个阶数参数.该模型在考虑时间维度特征的同时，考虑空间维度特征，但该模型的局限是无法处理空间维度的非平稳序列.

门限自回归(threshold autoregressive model，TAR)通过引入多个门限值将观测时空序列分成多个区间，对不同区间采用不同的自回归模型(autoregressive model，AR)，而这些模型的总和构成了整体观测时空序列的非线性动态描述，但TAR与线性模型无本质区别，其采用对整体序列分段线性化的表示.向量自回归模型(vector autoregressive model，VAR)由AR拓展而来，将AR中的单变量变为由多元时间序列组成的向量，可以实现多元时间序列预测任务，但该模型需要较多的参数估计，样本过少会导致预测精度较差.

3.2 基于传统机器学习模型的时空序列预测方法

时空序列预测的本质与传统机器学习中的回归分析存在着一定的联系，所以传统机器学习模型也常用于时空序列预测.

决策树(decision tree，DT)是一种树形结构，可以较好地捕获非线性特征.利用决策树进行时间序列预测主要对离散时间序列数据学习出决策树的结构，从而快速挖掘数据特征.2015年Kim等[14]设计一种决策树框架，通过滑动窗口将时空序列预测问题拆解，对多个固定长度的时空序列分别进行预测，从而学习出完整的时空序列预测器.

支持向量机(support vector machine，SVM)是一种二类分类模型，是建立在几何距离基础上的首个学习算法，在小样本上效果较好.2012年王佳璆等[15]在支持向量机核函数的基础上设计时空核函数，使得时空支持向量回归模型(spatial-temporal support vector regression，STSVR)可以很好地捕获时空特征.为更好解决时空序列数据的时空非平稳性，引入折扣最小平方法(discounted least squares，DLS)，通过配置不同的权重，最终完成对时空非平稳序列建模，在预测效果上优于传统STARIMA模型.

隐马尔可夫模型(hidden Markov model，HMM)由马尔可夫模型发展而来，在其基础上增加多个隐含状态，对于预测效果有较好提升.2016年刘姣姣等[16]提出一种基于时空密度聚类的隐马尔可夫模型对时空序列进行预测，首先识别原始序列中的噪声干扰，并得到序列的分段线性表示，然后利用基于密度的时空聚类算法(spatio-temporal density-based spatial clustering of applications with noise,ST-DBSCAN)进行聚类，获得多个隐含状态，最后利用隐马尔可夫模型对状态序列进行预测，并作为最终的时空序列预测结果.隐马尔可夫模型的加入，不仅可以捕获数据的时空相关性，还可以有效去除噪声，增加预测的准确度，可以较好地处理空间不平稳的时空序列数据.

3.3 基于深度学习模型的时空序列预测方法

3.3.1 深度学习模型

3.3.1.1 用于学习时间维度特征的深度学习模型

1)循环神经网络(recurrent neural network，RNN)和长短期记忆网络(long short-term memory，LSTM)

RNN是一类以序列数据作为输入，在序列演进方向上进行递归，且所有节点按链式连接的递归神经网络[17]，旨在识别顺序特征并使用先前的模式来预测下一个可能的情况，结构如图5(a)所示.前一个时间步的输出被输入到下一个时间步的网络中，即RNN具有记忆性，历史信息可以存储并传递给未来.同时RNN参数可以共享，对具有非线性特征的序列具有很好的学习能力，可以有效处理诸如时间序列分析、语音识别和自然语言处理等类问题，但是由于RNN存在梯度爆炸和梯度消失的问题，导致其仅具有短期记忆.

为了解决RNN存在的问题，提出LSTM，如图5(b)所示.设计特殊的存储单元，使其可以在更长的时间内记住输入的历史信息.LSTM由3个门组成，输入门可以控制是否允许新的输入，遗忘门控制忽略哪些不重要的信息，最后将信息通过输出门输出.该网络可以很好地学习输入数据的长期依赖，记住更长时间的历史数据信息.

LSTM的前向传播算法与RNN类似，将一个长度为T的时间序列作为输入数据，时间步长每前进一次，输出结果便更新一次.LSTM的后向传播算法也与RNN的类似，通过从时间序列末尾时刻开始，逐步反向循环计算各参数的梯度，最终用各时间步的梯度更新网络参数.RNN和LSTM均可以处理时间序列数据以学习时间依赖性，且已被广泛用于时空序列预测领域的研究[18-19].

2)序列到序列模型(sequence to sequence，Seq2Seq)

Seq2Seq模型最初是为机器翻译而设计提出，但它是一个通用框架，可以处理序列数据，并预测序列数据，即可以对固定长度的输入与固定长度的输出进行映射，输入序列的长度和输出序列的长度可以不等.如图5(c)所示，由编码器、中间向量和解码器三部分组成.由于Seq2Seq可以较好地捕获序列相关性，特别是时空序列数据呈现高度时间相关性，故Seq2Seq在时空序列预测领域被广泛应用.

3)受限玻尔兹曼机(restricted Boltzmann machines，RBM)

玻尔兹曼机是神经网络模型的一类，但实际中更多使用RBM，RBM本身结构很简单，如图5(d)所示，是一个具有2层的网络结构，上一层神经元组成隐藏层(hidden layer)，下一层神经元组成可见层(visible layer)，隐藏层和可见层之间是全连接的，但同一层中没有2个节点相互连接，且RBM一般是二值的，还具有权重.根据特定的任务，训练RBM，可用于降维、分类、特征学习以及协作过滤，较适用于对序列数据进行降维与特征学习.

4)自编码器(autoencoder，AE)

AE通过使用无监督方式学习输入数据的紧凑数据编码，如图5(e)所示，包括编码器和解码器两部分.其主要目的是将时间序列高维向量转化为低维向量，且学习得到的低维特征向量包含了高维时间序列的本质特征，是原始时间序列的良好表示.而评估AE的方法是重建误差，即最小化输出与原始输入数据间的误差.由多个堆叠式AE组成的堆叠式自动编码(stacked autoencoder，SAE)[20]在时空序列预测领域得到了广泛的应用.

图5 用于学习时间维度特征的深度学习模型Fig.5 Deep learning model for learning temporal-dimension features

3.3.1.2 用于学习空间维度特征的深度学习模型

1)卷积神经网络(convolutional neural network，CNN)

CNN是一种前馈神经网络，与普通神经网络非常相似，均由具有可学习的权重和偏置常量的神经元组成，但又异于普通神经网络，CNN默认输入是图像，通常包含输入层、卷积层、池化层、完全连接层和输出层，如图6(a)所示.首先将原始图像输入到卷积层中，通过内核中多个过滤器以提取不同的特征，然后将卷积之后维度较大的特征输入到池化层，池化层将特征切成几个区域从而得到新的且维度较小的特征，利用降采样操作以达到减少参数的目的.最后通过堆叠多个全连接层对特征进行非线性转换.

由于CNN可以很好地捕获空间特征，被广泛应用于时空序列预测领域[21]，特别是应用于从空间地图以及时空栅格数据中进行学习.其中三维卷积神经网络(3D CNNs)非常适合于时空特征的学习.相比较于二维卷积神经网络(2D CNNs)，3D CNNs能够通过3D卷积层和3D池化层在时空维度上进行卷积和池化操作，更好建模时空信息.而2D CNNs仅在空间上完成学习任务，没有充分利用时间维度的运动信息.也就是说，3D CNNs得益于3D卷积和3D池化，在2D CNNs对时间维度特征提取的基础之上，具备抽取空间维度信息特征的能力.

2)图卷积网络(graph convolutional network，GCN)

由于传统CNN通常用于处理结构化数据以提取空间特征，如图片数据等，而无法处理抽象意义上复杂的拓扑图结构，于是出现图卷积神经网络[22]，GCN本质便是用来提取拓扑图结构的空间特征，如图6(b)所示.GNN的本质工作就是特征提取，并在图神经网络的最后实现图嵌入，即将图结构转化为特征向量矩阵.首先将卷积操作应用于图中每个节点的邻居节点，然后进行池化操作，再堆叠多个图卷积层，挖掘远跳节点的更多信息，以节点潜在嵌入形式进行存储.在生成图中节点潜在嵌入后，馈入前馈网络以实现节点分类或者回归等目标，也可以汇总所有已存储的节点嵌入从而呈现整个图结构，然后对整个图进行分类或回归操作.

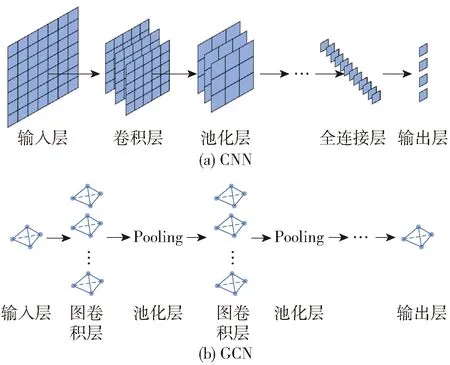
图6 用于学习空间维度特征的深度学习模型Fig.6 Deep learning model for learning spatial-dimension features

将GCN直接应用于图结构数据，可以很好地捕获拓扑图结构中节点间的相关性，以及节点的特征，即可以在空间维度上提取具有高度意义的模式和特征，同时可以利用时间轴上整个卷积结构来捕获时间维度的动态特征.因此GCN适用于处理图结构的时空序列数据[23]，如脑网络数据和交通流量数据等.

3.3.2 深度学习模型选择

本小节对目前深度学习应用于时空序列预测领域内的文献进行分类总结，并将文献中涉及的不同模型对应于不同的数据类型.图7继续总结了不同数据表示形式所对应的不同深度学习模型，表2对目前使用深度学习模型处理不同类型的时空序列数据的工作进行分类总结.

表2 基于部分现有文献对于处理不同时空序列数据的深度学习模型的分类总结Table 2 Classification and summary of deep learning models used for processing different spatio-temporal sequence data based on part of the existing literature

图7 不同数据格式对应的深度学习模型Fig.7 Deep learning models with different data formats

RNN和CNN这2种深度学习模型通常用于轨迹数据预测.轨迹的一种直接表示方式为一系列位置，从而可以使用RNN和LSTM模型对于位置序列完成预测任务.2018年Jiang等[24]提出一种基于RNN的深度序列学习模型，通过给定一个人先前访问过的位置，预测其下一步的目的地，完成城市地区人口流动预测问题.2018年Xu等[25]通过无碰撞LSTM对经典LSTM进行扩展，共享相邻行人的隐藏状态，完成人体轨迹的位置预测.2019年Pang等[26]引入具有LSTM块的RNN模型，学习公交车行驶轨迹中的远程依赖关系，完成对公交车到站时间的预测问题.轨迹的另一种表示方式为矩阵，从而可以应用CNN更好地捕获空间相关性.2018年Lü等[27]将轨迹建模为二维图像，每个像素点代表轨迹中是否访问了相应位置，然后采用多层卷积神经网络并结合多尺度轨迹模式，完成对轨迹目的地的预测.同年Karatzoglou等[28]提出一种基于CNN的方法对语义轨迹进行学习，其中轨迹中访问的位置都与语义相关联，语义轨迹被建模为一个矩阵，然后输入到CNN模型中，学习潜在特征，完成对用户将来可能访问到的位置的预测.

RNN和LSTM被广泛用于时间序列数据预测，其中时间序列数据通常不包含空间信息，因此对于时间序列的预测模型中未明确考虑空间相关性.通常可以将道路上的交通流量数据、风速温度等气象数据建模为时间序列，然后应用深度学习模型.2019年Rodrigues等[29]提出一个具有全连接层的深度学习模型，从出租车需求的历史时间序列中学习特征，并以时间序列对特定区域的出租车需求进行建模，完成需求预测任务.2018年Cheng等[30]提出了一个集成模型，集成传统风速预测模型，包括小波阈值降噪(wavelet threshold de-noising，WTD)和带有RNN的自适应神经模糊推理系统(adaptive network-based fuzzy inference system，ANFIS)，从而完成对风速的预测.

空间地图可以表示为图像矩阵，适用于CNN处理多种预测学习任务[31].2016年Zhang等[32]提出了一个基于CNN的人群流量预测模型，该模型的输入是人群流动空间图，完成城市实时人流量预测任务.2018年Wang等[33]提出一种跨域卷积神经网络(cross domain convolutional neural network,CD-CNN)，将人们的位置表示为空间地图，作为模型的输入，以完成从移动电话信号数据中识别出居民的本地/移民属性.

为了同时捕获时空地图的时间和空间相关性，研究人员尝试将CNN和RNN结合以进行预测.2015年Shi等[34]提出卷积LSTM模型(ConvLSTM)，该模型将CNN与LSTM融合，形成一个序列到序列的预测模型，以完成降水邻近预报任务，且模型的输入输出均为空间地图矩阵.2018年Zhou等[35]提出一种深度学习网络，将城市单元格中的乘客需求建模为空间图，利用由ConvLSTM组成的编码器-解码器框架用于学习数据中的时空特性，从而以端到端的方式完成按需移动性服务中乘客的接送需求.

此外还可以使用其他模型对空间地图进行预测，如GCN、生成对抗性网络、ResNet以及混合方法.2018年Li等[36]提出一种扩散卷积循环神经网络(diffusion convolutional recurrent neural network，DCRNN)模型，将交通网络建模为图结构，DCRNN采用双向随机游走的方式捕获节点间的空间依赖性，完成对交通流量的预测任务.2019年Zhang等[2]引入时空加权图(spatial-temporal weighted graph，STWG)，并首次研究如何将CNN和对抗学习进行组合，以完成城市交通流量预测任务.

时空栅格数据既可以表示2个维度的位置和时间的矩阵，也可以表示为三维张量，通常使用2D-CNN和3D-CNN，或者将它们与RNN结合在一起进行预测.2019年Zhang等[37]提出了一种多通道3D立方体连续卷积网络，称为3D-SCN，完成通过3D雷达数据及时预报风暴信息.2018年Shen等[38]提出将城市中不同时隙中乘客的移动性事件建模为3D张量，然后利用3D-CNN模型完成对运输乘客供求情况的预测.

3.4 时空序列预测方法对比

传统参数模型以及传统机器学习模型可处理数据的能力有限，适合少量数据以及小样本数据，而现今由于数据量的爆炸式增长，以数据驱动的深度学习模型适用于对海量数据进行有效挖掘.

传统参数模型以及传统机器学习模型需要手动选择特征，而深度学习方法具有强大的自主特征表示能力，可以以监督或无监督的方式从原始数据中自动学习特征，捕获隐藏的线性以及非线性关系.

在数据处理方面，一种类型的深度学习模型可以处理多种不同类型的时空序列数据，执行多种不同的时空序列预测任务.如RNN以及LSTM可以处理轨迹数据[39]和时间序列数据[96]，CNN可以处理轨迹数据[28]、空间地图数据[60]以及栅格数据[97]等.而传统参数模型以及传统机器学习模型由于特征学习能力的限制，一种模型通常只可以对一种时空序列数据建模.

深度学习模型可以很好地学习历史时空序列数据间的时空相关性.对于时间维度，深度学习模型可以有效捕获长短期时间依赖[90]，而传统参数模型以及传统机器学习模型在面对多尺度高维数据时表现较差，较难准确捕获时间依赖；对于空间维度，深度学习模型可以有效捕获局部以及全局的空间依赖[98]，而传统参数模型以及传统机器学习模型仅可捕获相邻节点间的局部空间相关性[99].

在3种用于时空序列预测的模型中，传统参数模型对事物演进的机理过程进行建模，需要研究人员具有充足的领域知识以及丰富的实践经验，才可以精准建模，从而得到比较精确的预测结果.传统机器学习模型也需要一定的先验知识，以辅助模型预测.而深度学习模型因为具有强大的特征学习的能力，可以通过自动捕获数据间的相关性，所以其几乎不需要任何领域知识.

深度学习模型最大的一个特点就是准确率高.如在交通流量预测任务中，与ARIMA方法相比，DBN方法的平均绝对误差(mean absolute error，MAE)降低50%以上[100].在交通速度预测任务中，基于LSTM方法的预测误差被证明远小于SVM、卡尔曼滤波器和ARIMA的误差，仅为5.95，而后者分别为15.30、20.11和19.98，但深度学习模型也具有一定的局限性.正是因为3种模型所依赖领域知识的程度不同，导致每种模型对于时空序列的预测结果的可解释性不同，其中传统参数模型的可解释性最高，而深度学习模型通常被视为一个黑盒，在可解释性方面远不如传统参数模型和传统机器学习模型.对比总结见表3.

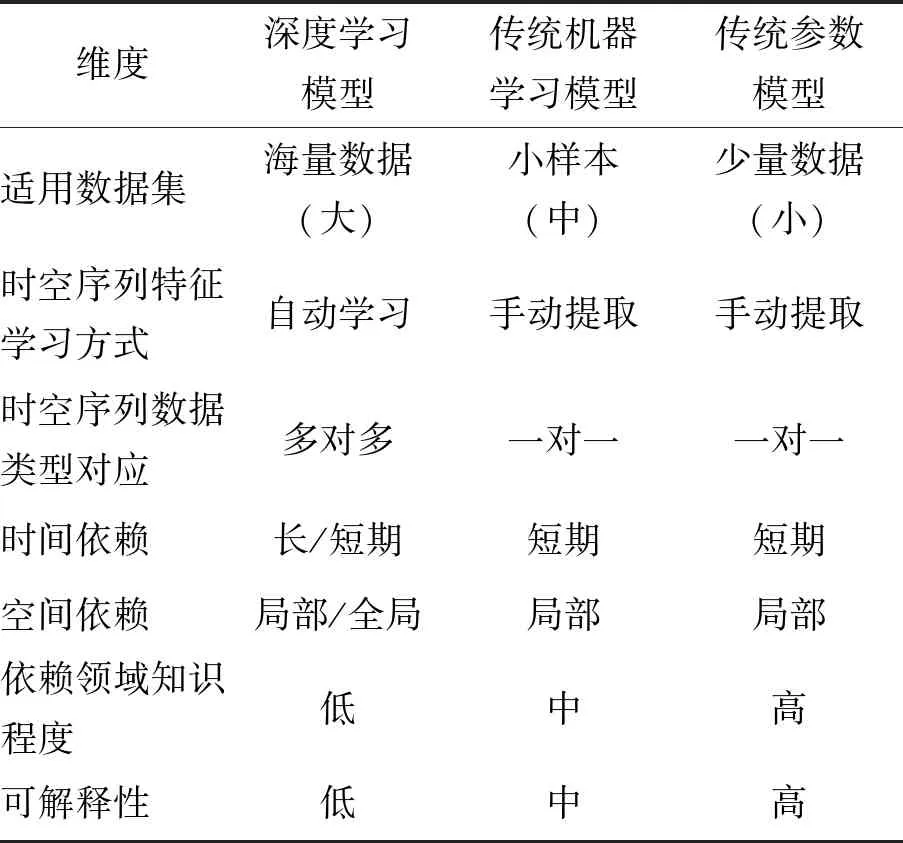
表3 深度学习模型与传统机器学习模型、传统参数模型对比总结Table 3 Comparison and summary of deep learning models,traditional machine learning models and traditional parameter models

除此之外，深度学习模型对数据和计算资源要求较高，而主流的深度学习框架，如TensorFlow和PyTorch则提供CPU和GPU运行环境，允许用户自定义使用，在一定程度上缓解该问题，此外还有初始化参数以及参数调整等一系列问题，由于深度学习的训练过程很慢，因此在参数的确定上需要大量的工程经验以及专业知识以提高训练效率.

4 深度学习模型在时空序列预测中的应用

4.1 交通科学领域

随着各种传感器广泛应用，交通领域的时空序列数据逐渐丰富，同时也变得可用，通常包括交通速度、交通量、交通事故，以及路段、区域以及时间信息.这些交通数据可以是不同场景下的事件数据、时间序列数据、空间图数据或栅格数据，需要深度学习来对数据间复杂的线性或非线性关系进行挖掘并做出预测等工作，如对交通流量进行预测[1,2,101]，对交通拥堵进行预测[74]，对交通事件进行预测[43,78]等.

在交通流量的预测中，可以将不同传感器的数据建模为时间序列，在每组传感器的数据上利用RNN或者LSTM进行学习并预测[51]，还可以将时空序列建模为栅格矩阵，其中一个维度是各个传感器的位置，另一个维度是时间[102]，也可以将时空序列数据建模为空间图结构，然后使用GCN进行预测[103].此外，由于融合模型具有一定的优势，也广泛应用于交通流量预测领域.

4.2 气候科学领域

在气候科学领域，时空序列预测被广泛应用于长短期天气预报，对于已收集到的气象数据，如温度、风向、大气压强等，研究学者们也已进行了相应的研究.

由于不同站点、不同传感器收集到的气象数据具有很强的时空相关性，因此深度学习对时空序列的预测方法在该领域应用广泛，如空气质量预测[3,55]、风速预测[104-105]、降水预测[34]，以及极端天气预测[106-107]等.与气候相关的数据类型可以是空间图数据，如遥感图像[67]，可以是时间序列数据，如部署在空间中传感器采集到的监测数据[30]，还可以是事件数据，如极端天气事件.对天气的长短期预报以及极端天气预测的研究，可以挖掘其中规律，帮助相关管理部门掌握未来一段时间内的气候变化趋势，对提前做出科学防治措施以及人们的日常出行具有指导意义.

4.3 神经科学领域

在神经科学的研究中，引入并使用多种技术，例如脑功能共振成像(functional magnetic resonance imaging，fMRI)、脑电图(electroencephalogram，EEG)，以及脑磁图(magnetoencephalography，MEG)和功能性近红外光谱(functional near infrared spectroscopy，fNIRS)，通过使用这些技术对连续的神经活动进行监测.由于技术不同，采集到的数据时空分辨率也大有不同，如fMRI是通过数百万个位置对神经活动进行监测，而EEG则是通过数十个位置对神经活动进行监测.fMRI监测间隔是每2 s进行一次测量，而EEG则是每1 ms对神经活动进行一次测量.

对于如此复杂的时空序列数据，深度学习模型在该领域被广泛应用.图像数据可以表示为空间图或栅格数据，然后使用深度学习模型分析这些神经影像数据，从而解决神经科学中研究的许多问题，如疾病分类以及诊断任务[57,108]，基于脑激活的分类[58,95]，以及基于脑功能网络的分类[8,61]等.

4.4 犯罪分析领域

犯罪事件是影响社区生活和经济发展的社会问题之一，犯罪事件可分为几种类型，如盗窃、抢劫这类针对于财产的犯罪事件，还有凶杀、殴打、强奸这类的侵略罪.为减少犯罪事件的发生，越来越多的城市选择将执法机构持有的犯罪数据公开，以方便研究.犯罪数据通常包括犯罪类型，事件发生的时间、地点，罪犯信息，以及受害者等相关信息，犯罪数据是典型的事件数据，可以通过构建相应的实例输入到深度学习模型，以捕获犯罪数据间的时空相关性，进而执行预测任务[62]，还可以通过在时空域对数据进行整合，从而形成空间地图数据，再应用深度学习模型执行预测任务.

4.5 按需服务领域

按需服务通过实时为人们提供所需的服务，接管了众多传统领域，如滴滴、Uber等平台的兴起，平台在解决用户需求的同时，还积累了大量时空序列数据，包括客户所需服务类型、客户位置，以及所需服务时间等，也为进一步发展和完善按需服务提供一定的数据基础.

为了更好满足客户的需求，需要使用深度学习方法准确地预测不同位置和不同时间下客户对不同类型服务的需求，以及各平台的供应能力[71,109]，通常划分不同的区域，并将各区域的服务需求建模为空间地图数据或张量数据，输入到深度学习模型当中，执行特征学习以及需求预测任务.

4.6 流行病学领域

广泛存储在各个医院中的电子健康数据可以表示为时空序列数据集，该数据集包括与患者相关的人口统计信息以及相应的诊断信息，而这些信息都有相对应的地理空间信息，可以根据不同类型的疾病以及传染病构建模型进行预测，以发现不同疾病的时空分布[110].对于流行病学的研究，可以帮助人们尽早发现流行病的发生与传播，方便决策者制定有效政策，出台相应措施，尽最大可能降低损失以保证人民的生命安全.

5 进一步研究方向

1)时空序列数据的预处理：由于时空数据源的差异，且数据在传输和存储的过程中存在错误和丢失现象，导致时空序列数据集中存在缺失值、噪声数据，以及空间数据尺度不一致现象，而时空序列数据与传统的关系数据之间存在差异，将处理传统关系数据的方法直接应用于时空序列数据集的预处理效果较差，需要有针对性的方法来对时空数据进行处理.同时，为了获得更加精准的预测结果，可以对多模态时空序列进行集成，将多种不同数据有效地融合在一起，进而帮助模型更好更全面地捕获时空特征.

2)深度学习模型的选择：由于不同领域时空序列数据类型不同，目前缺乏如何根据不同数据类型选择并构建相应的深度学习模型的研究，从而使时空序列预测的建模过程变得具有方向性和指导性.

3)深度学习模型的可解释性：可解释性可以使模型以更易于人们理解的方式呈现模型的预测行为，而深度学习模型通常被认为是黑盒，所以如何为时空序列预测构建具有可解释性的深度学习模型对人们认识并学习某事物的变化机理过程具有很重要的指导意义.

6 结论

1)本文给出如何根据不同时空序列数据类型选择不同深度学习模型建模的指导.首先介绍时空序列数据，包括数据的属性、类型，并给出对应的数据实例以及表示形式，然后介绍目前用于时空序列数据的预处理方法，提高现有数据集的质量，并给出不同数据表示与不同深度学习模型之间的对应关系，以方便研究人员对模型进行选择，完成相应的预测任务.

2)本文总结有关深度学习应用于不同领域内时空序列预测任务的最新进展，包括交通运输、气候科学、神经科学、犯罪分析、按需服务，以及流行病学领域.

3)本文强调目前深度学习在时空序列预测任务中仍存在的不足：缺少有针对性的时空序列数据的预处理方法，缺少对数据建模的指导，以及缺少对深度学习模型预测结果的可解释性，未来需要对上述未解决问题进行深入研究.