结构不良型题、开放探究题狂练
1.已知△ABC的内角A,B,C的对边分别为a,b,c,满足有三个条件:其中三个条件中仅有两个适合,请选出适合的条件完成下面两个问题:
(1)求c;
(2)设D为BC边上一点,且AD⊥AC,求△ABD的面积.

2.在①(a+b)(a-b)=(a-c)c,②2ac=2bcosC,③(a-bcosC)=csinB三个条件中任选一个,补充在下面的问题中,并解答.
问题:在△ABC中,内角A,B,C的对边分别是a,b,c,且满足________,b=
若a+c=4,求△ABC的面积.

3.从①前n项和Sn=n2+p(p∊R),②a6=11且2an+1=an+an+2这两个条件中任选一个,填至横线上,并解答.
在数列{an}中,a1=1,______________,其中n∊N*.
(1)求数列{an}的通项公式;
(2)若a1,an,am成等比数列,其中m,n∊N*,且m>n>1,求m的最小值.

4.给出以下三个条件:
①数列{an}是首项为2,满足Sn+1=4Sn+2的数列;
②数列{an}是 首项为2,满足3Sn=22n+1+λ(λ∊R)的数列;
③数列{an}是 首项为2,满足3Sn=an+1-2的数列.
请从这三个条件中任选一个将下面的题目补充完整,并解答.
设数列{an}的前n项和为Sn,an与Sn满足____________,
记数列bn=log2a1+log2a2+…+log2an,cn=,求数列{cn}的前n项和Tn.

5.在①△ABC的面积S△ABC=2,②∠ADC=这两个条件中任选一个,补充在下面问题中,并解答.
问题:如图,在平面四边形ABCD中,∠ABC=,∠BAC=∠DAC,___________,CD=2AB=4,求AC.
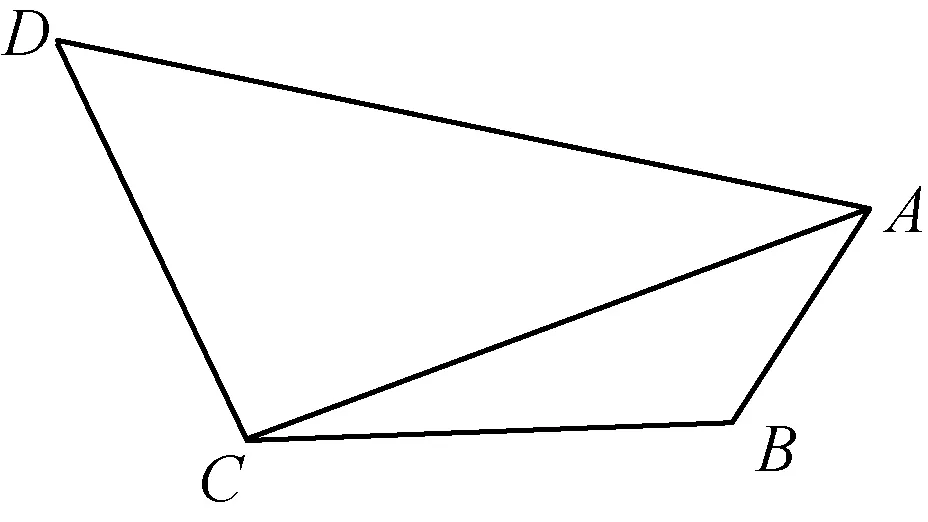
(第5题)

6.在等差数列{an}中,已知a6=12,a18=36.
(1)求数列{an}的通项公式an;
(2)若___________,求数列{bn}的前n项和Sn.
在①bn=②bn=(-1)n·an,③bn=·an这三个条件中任选一个补充在第(2)问中,并对其求解.

7.已知△ABC的各边长为3,点D,E分别是AB,AC上的点,且满足,D为AB的三等分点(靠近点A,如图1),将△ADE沿DE折起到△A1DE的位置,使二面角A1-DE-B的平面角为90°,连接A1B,A1C(如图2).
(1)求证:A1D⊥平面BCED;
(2)在线段BC上是否存在点P,使直线PA1与平面A1BD所成的角为60°? 若存在,求出PB的长;若不存在,请说明理由.
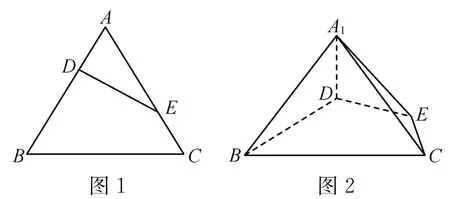
(第7题)

8.如图1,在菱形ABCD中,∠ABC=120°,动点E,F在边AD,AB上(不含端点),且存在实数λ使=,沿EF将△AEF向上折起得到△PEF,使得平面PEF⊥平面BCDEF,如图2所示.
(1)若BF⊥PD,设三棱锥P-BCD和四棱锥P-BDEF的体积分别为V1,V2,求
(2)试讨论,当点E的位置变化时,二面角E-PF-B是否为定值.若是,求出该二面角的余弦值;若不是,说明理由.
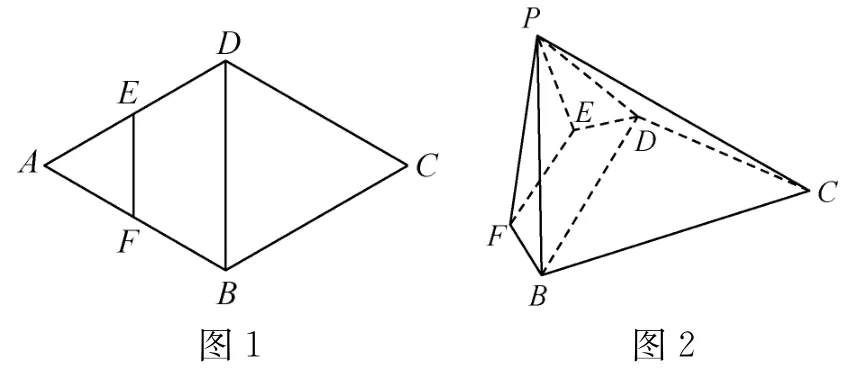
(第8题)

9.已知A,B分别为椭圆E:(a>1)的左顶点和下顶点,P为直线x=3上的动点,的最小值为
(1)求E的方程;
(2)设PA与E的另一交点为D,PB与E的另一交点为C,问:是否存在点P,使得四边形ABCD为梯形? 若存在,求P点坐标;若不存在,请说明理由.

10.已知A(0,2),B(0,-2),P为坐标平面内一动点,直线PA,PB的斜率kPA,kPB满足:kPA·kPB=
(1)求动点P的轨迹E的方程;
(2)过E上一点N作不与坐标平行的直线与E相切,交x轴于点D,O为坐标原点,试确定y轴上是否存在定点Q,使得|cos∠DNQ|=sin∠ODN? 若存在,请求出点Q的坐标;若不存在,说明理由.


