30%BMCR工况下超临界锅炉水冷壁水动力安全性评估
倪晓滨,周克毅,徐青蓝
(东南大学 能源与环境学院,南京 210096)
近年来,为了大力推进能源结构清洁化改革,新能源发电发展加快,而火电发展放缓。但新能源发电具有随机性、间歇性、不稳定性等特点[1],其占比增加到一定程度后,必然给电网带来更大的调峰压力,现有火电机组需要充分挖掘系统调峰能力,着力增强系统灵活性、适应性[2],这是现在及未来火电不可避免的发展趋势。其中,深度调峰能力和低负荷运行适应性是制约火电机组灵活性提升的重要因素[3-5],深度调峰要求机组负荷率低至20%~40%。
由于超临界机组在设计之初往往只考虑最低40%~50%最大连续蒸发量(BMCR)工况正常运行,在偏离设计工况的超低负荷下水冷壁水动力有可能出现脉动、多值性等安全问题[6-7]。目前,已有的研究多针对垂直管圈水冷壁锅炉[8-12],且对30%BMCR工况以下的研究较少。笔者以某650 MW超临界螺旋管圈水冷壁锅炉为例,建立了水冷壁螺旋管圈单管热负荷计算模型与螺旋管圈水冷壁流量与压力节点的等效回路法计算模型,计算了低负荷下水冷壁的水动力特性,对30% BMCR工况下的水动力安全性进行评估,为同类型锅炉适应深度调峰运行可行性分析提供依据。
1 计算模型
该锅炉为650 MW一次中间再热、超临界压力变压运行带内置式再循环泵启动系统的本生直流锅炉,炉膛水冷壁均为光管,燃烧器采用前后墙对冲燃烧方式。
图1为水冷壁流程(φ559×95表示外径为559 mm、壁厚为95 mm的管子,同其他处标注),下部水冷壁为螺旋管圈(共436根),经中间集箱汇合后垂直上升进入上集箱,再分别通过折焰角、水平烟道包墙与连接管进入4个分离器。
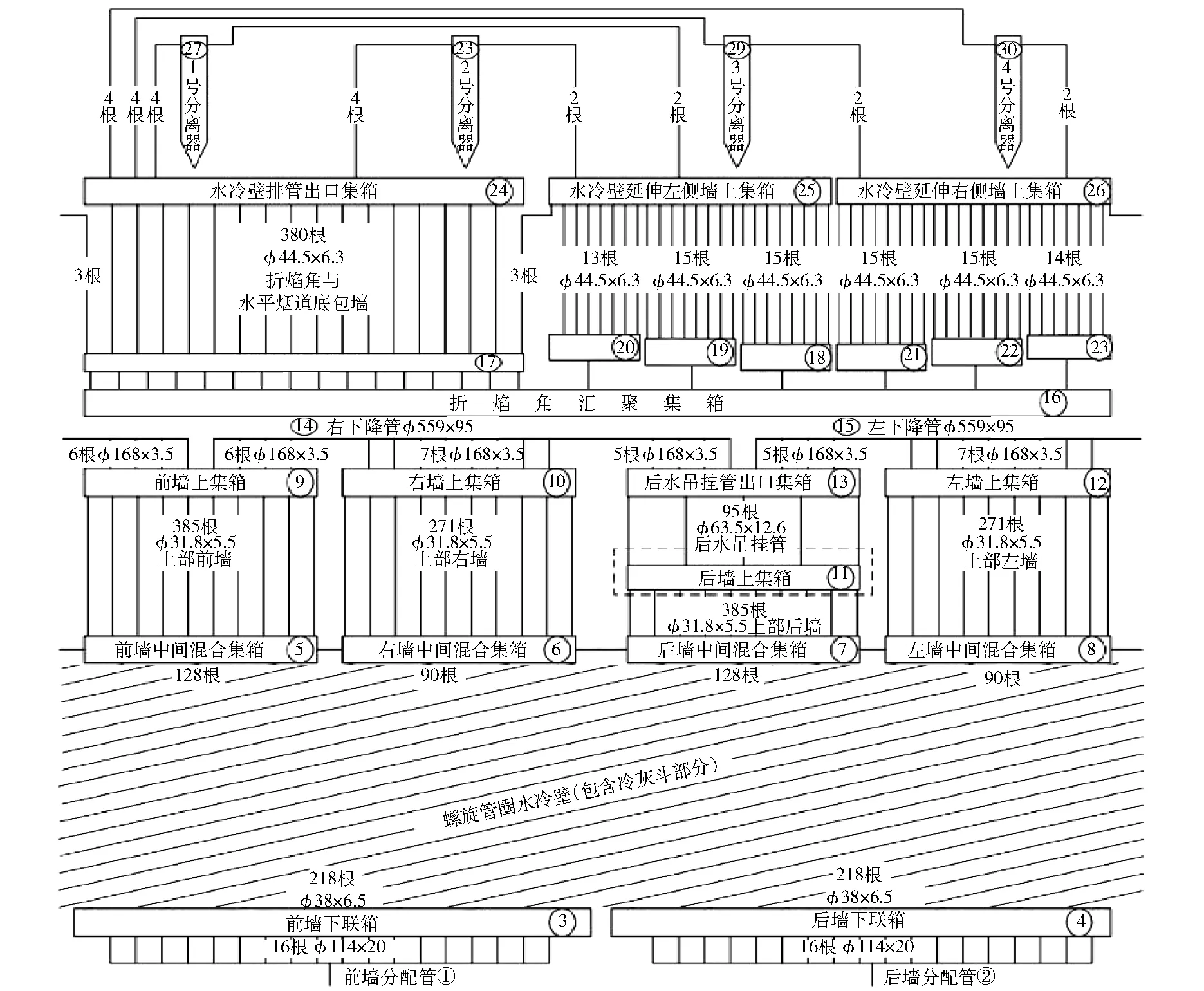
图1 水冷壁流程
1.1 亚临界压力下水动力计算
锅炉水冷壁水动力计算是指在一定热负荷、水冷壁总流量条件下,确定水冷壁内各管路流量与压降的关系,可用于分析工质的流动特性及传热的安全性。亚临界压力下水动力计算可分为以下5个步骤:
(1)划分管路流动网络,假设支路流量与各节点压力。
(2)由各管段热负荷、流量、入口温度、入口压力与出口压力计算出口干度,判断管内工质是否发生相变。
(3)假设相变点压力计算得到管内工质各段平均比体积、平均干度与其他物性参数,并计算得到该管路水段、两相段、汽段的压降,从而校正相变点压力,最后计算管路出口参数。
(4)以此类推计算水冷壁出口压力,比较整个水冷壁和各管屏的新压降与旧压降,检验误差。
(5)若误差过大,则重新分配压力与流量,并重复第2~3步;若误差满足要求,则计算完成。
螺旋管圈水冷壁结构复杂,管子与管子之间、管子与集箱之间的连接弯头多,流动阻力大;在BMCR工况运行时,工质的质量流速较大,阻力的影响相对较小;在超低负荷运行时,阻力扰动相对较大,可能对水动力特性造成影响。因此,在水动力计算过程中,要求要有更高的计算准确度。水冷壁流量与压力计算模型、局部热负荷的确定与单管热负荷计算模型直接关系到计算结果的准确性。
1.2 复杂水冷壁流量压力节点的等效回路法
超临界螺旋管圈水冷壁有多个集箱,集箱与集箱之间存在交叉回路,在水动力计算过程中,阻力系数的计算复杂而繁琐。因此,采用等效流动网络方法,将水冷壁流程简化为集箱节点与集箱间管路的组合(见图2),其中:圆圈代表集箱(zj为中间混合集箱,fl为等效4个分离器的单个集箱),连线代表集箱与集箱之间的管路或管组。
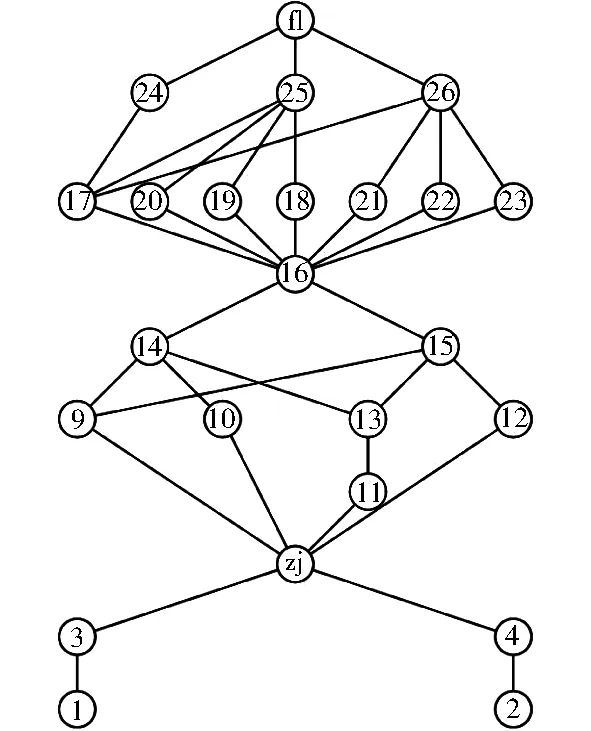
图2 水冷壁流动网络
已知单个管路压降流量关系方程为:
(1)
式中:Ki为管路i的折算阻力系数[13],kg-1·m-1,由局部阻力折算系数、摩擦阻力折算系数、重力压降折算系数相加得到;qmi为管路i的质量流量,kg/s;Δpi为管路i的压降,Pa。
由并联管路压降相等的关系可得并联管路的总折算阻力系数Kb为:
(2)
由串联管路流量相等的关系可得串联管路的总折算阻力系数Kc为:
Kc=∑Ki
(3)
由于螺旋管圈结构的复杂性,出口集箱通常处于交叉节点,即1个集箱前后经过多条管路,此时该集箱前后管路流量不相等,无法等效为1条回路。故而采用等效支路的方法,将1条回路等效为多条支路,等效支路的折算阻力系数K′可表示为:
(4)
式中:qmz为该管路总质量流量,kg/s;qmj为等效支路j的质量流量,kg/s;K为等效流量下的折算阻力系数。
通过式(1)~式(4)可以将整个水冷壁回路等效为1条回路,从而计算得到水冷壁总压降。该模型可以避免对复杂水冷壁的每条回路进行繁琐的计算,在减少总计算量的同时避免了计算单条回路时的误差,提高了计算模型的效率与稳定性。
1.3 局部热负荷不均系数的确定
锅炉在低负荷运行时,炉膛内火焰充满度差,此时沿高度热负荷分布偏离经验曲线较多。目前,在水动力计算文献中大多采用经验曲线[14-15],或者通过已有的温度测点数据来反算热负荷[16]。笔者采用炉膛分段热力计算的方法,通过计算拟合得到炉膛沿高度方向的热负荷不均系数。
将炉膛由冷灰斗二分线至顶棚管中心线分为七段,经拟合计算后得到每段水冷壁受热面平均热负荷见图3(相对高度为局部高度占总高度的比)。

图3 炉膛局部热负荷不均系数拟合
拟合得到沿高度方向热负荷不均系数的6次多项式方程:
ηrh=176.04h6-573.4h5+699.86h4-
383.61h3+81.066h2+0.000 1h+0.303 2
(5)
式中:ηrh为沿高度方向的炉膛热负荷不均系数;h为相对高度。
从理论角度难以确定下炉膛各墙管屏沿宽度方向的热负荷分布,故而采用BMCR工况下螺旋管圈出口外壁温度的测点数据对经验曲线进行修正。上炉膛各墙沿宽度方向的热负荷不均系数分布则采用原苏联《锅炉热力计算标准方法》中的经验曲线。图4为修正后的下炉膛前墙和右墙沿宽度方向的热负荷不均系数。

图4 修正后下炉膛前墙和右墙沿宽度方向的热负荷不均系数
1.4 螺旋管圈水冷壁单管热负荷计算模型
水冷壁受热管段可大致分为垂直上升管段与倾斜上升管段。在实际运行中,水冷壁管子存在燃烧器喷口、温度探测孔及吹灰孔等外绕处,这些位置往往有绝热措施防止局部高温,在计算中需要考虑非受热管段。对2种管子建立物理模型(见图5)。
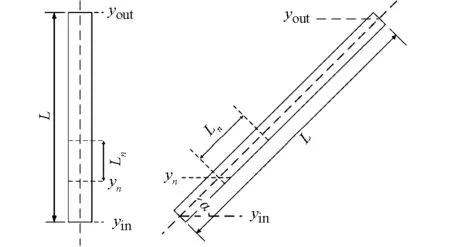
yin—入口相对高度坐标;yout—出口相对高度坐标;L—计算管段长度;yn—第n段非受热管段入口相对高度坐标;Ln—第n段非受热管段长度;α—微元管段倾角。
与垂直管路相比,螺旋管圈单管在沿高度与宽度方向上的受热均在变化,考虑采用线积分法计算螺旋管圈单管热负荷。取螺旋管段微元建立数学模型(见图6)。

dL—微元管段的的长度;x、y—微元管段的相对宽度坐标、相对高度坐标。
该微元管段热负荷不均系数η为:
(6)
式中:ηrq为墙间热负荷不均匀系数,对于同一面炉墙可视为常数;ηrh可表达为关于炉膛相对高度的6次多项式F1(y);ηrb为沿宽度方向的热负荷不均系数,采用经验曲线,可表达为关于炉膛相对宽度的6次多项式F2(x);C为修正系数;C′为所有常数相乘后的系数。
该螺旋管段微元段的工质焓增dhr为:
(7)
式中:qav为水冷壁受热面平均热负荷,kJ/(s·m2);dF为微元管段受热面积,m2;qm为管子质量流量,kg/s;X、Y分别为该微元管段的宽度坐标、高度坐标,m;D为该管子截距,m。
通过转换坐标可得:
(8)
F3=F1(y)·F2[(y-yin)cotα+xin]
式中:xin为微元管段入口位置的相对宽度坐标;B为微元管段所在管屏的宽度,m;H为炉膛高度,m。
对式(8)进行积分可得螺旋管段单管焓增Δhr为:
(9)
通过式(9)利用计算机的运算能力可以对螺旋管圈每根管子进行单独的热负荷计算,从而确定单根管子的受热情况,确保每根管子压降与质量流量关系的准确性。
2 30%BMCR工况水动力
2.1 模型验证
为确定计算模型的准确性,选取40%汽轮机铭牌工况(TRL工况)和30% BMCR工况计算水动力,工况输入参数见表1。

表1 输入参数
烟气侧对流受热面由于热负荷比水冷壁小,且烟气与工质传热过程较短,故将其视为沿管长均匀吸热,表2为各对流受热面平均热负荷计算值。

表2 对流受热面平均热负荷
根据水动力计算得到水冷壁各管路的流量,结合热负荷分布曲线,计算螺旋管圈水冷壁出口外壁温度。图7为下炉膛前墙和右墙水冷壁出口外壁温度测点值与计算值(管路编号顺序从小到大依次为两墙外视从左到右的顺序)。前墙宽度为22.187 m,共有128根管子;右墙宽度为15.632 m,共有90根管子。每6根管子取1个测点作为现场温度测点(前后墙中前2个与后2个测点取5根),计算该6根管子温度计算值的平均值作为结果来比较测点值与计算值。由图7可得:40%TRL工况下,下炉膛螺旋管圈水冷壁出口外壁温度计算值与测点值基本相同,且与BMCR工况下的测点值沿管屏宽度的变化趋势基本一致,表明水动力计算模型有较高的准确性。在低负荷时,个别测点存在偏差,这是沿宽度方向上的热负荷分布不均所引起的,主要原因有:(1)低负荷时炉膛内火焰充满度下降,燃烧存在不确定性;(2)燃烧器低层运行、高层备用时,燃烧器喷口煤粉浓度有差异。

图7 螺旋管圈水冷壁前墙和右墙出口外壁温度分布
2.2 30%BMCR工况下水动力计算
经过验证后的计算模型用于计算30%BMCR工况下的水动力,30%BMCR工况输入参数见表1。表3为30%BMCR工况下水冷壁各参数计算值与设计值的对比,水冷壁总压降与分离器各参数误差均在可接受范围内。

表3 30%BMCR工况水动力计算值与设计值
图8为30%BMCR工况下下炉膛螺旋管圈与上炉膛垂直管圈的质量流速分布,下炉膛螺旋管圈按出口所在区域划分墙面。其中,下炉膛(见图8(a))的前后墙每8根管子取1条回路,左右墙每9根管子取1条回路;上炉膛(见图8(b))的前墙每11根管子取1条回路,后墙每5根管子取1条回路,左右墙每10根管子取1条回路。回路编号从小到大的顺序均为外视炉墙从左到右的顺序,下炉膛共52条回路,上炉膛共108条回路。
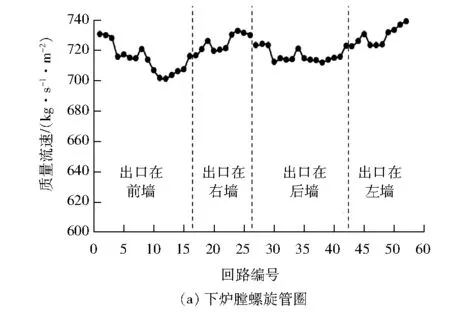
图8 质量流速分布
由图8(a)可得:下炉膛螺旋管圈质量流速最大处为出口在左墙的第52条回路,质量流速为739.03 kg/(s·m2),最小处为出口在前墙的第12条回路,质量流速为701.25 kg/(s·m2),两者相对偏差为5.11%。在螺旋管圈中,各管子的垂直高度差一样,最大重力压降为0.057 28 MPa,最小重力压降为0.053 96 MPa,重力压降相差不大,同时管子螺旋上升均走过1.5个全周,受热均匀,说明引起质量流速偏差的主要原因为结构不均(管长不均),即受到燃烧器喷口、分离燃尽风(SOFA)喷口等位置外绕管子影响。
由图8(b)可得:上炉膛垂直管圈质量流速最大处为出口在右墙的第43条回路,质量流速为399.689 kg/(s·m2),最小处为出口在左墙的第86条回路,质量流速为303.75 kg/(s·m2),相对偏差为24.00%,侧墙的质量流速偏差比前后墙更大,这是由于两侧墙同时存在辐射受热面与对流受热面,且受到了折焰角的影响(见图9),两侧墙靠近水平烟道侧的管子受热相对较少,使得管子中的两相段长度增加,流动阻力增加,工质流速减小,说明引起质量流速偏差的主要原因为吸热不均。

图9 30%BMCR工况下上炉膛水冷壁工质焓增分布
结合图8(b)与图9可得:在上炉膛管子内,工质的质量流速更小、偏差更大,主要原因为流通面积的改变与上下炉膛的热负荷存在差异。热负荷差异在超低负荷时会更明显,这是因为在超低负荷运行时,为了保持炉膛内的稳定燃烧,通常只投运下层燃烧器,使炉膛内热量集中在下炉膛。
3 30%BMCR水动力安全性校核
3.1 水动力多值性校核
水动力出现多值性是指管子或管组在一定热负荷下,由于管内工质比体积的变化,使得流量从一个稳定值转变至另一个稳定值的现象。当管子或管组表现出水动力多值性时,会使得管内工质流量出现非周期性变大或变小的情况,带来相变点的波动导致金属疲劳破坏,也可能使得管子出口工质产生相变引起过热。水动力多值性多发生在蒸发区受热面中,故选取下炉膛螺旋管圈水冷壁受热最强[17]的第149号管子进行单管水动力多值性校核。
水动力多值性的校核方法分为定性校核与绘制曲线校核,定性校核[17]是判断管子入口工质欠焓能否满足下式:
(10)
式中:h1为管子进口工质比焓,kJ/kg;h′、h″分别为管子出口压力对应下的饱和水比焓、饱和蒸汽比焓,kJ/kg;v1为管子进口工质比体积,m3/kg;v′、v″分别为管子出口压力下的饱和水比体积、饱和蒸汽比体积,m3/kg。
经计算,该管子入口工质欠焓为88.02 kJ/kg,式(10)右侧计算结果为142.90 kJ/kg,满足要求。图10为改变第149号管子质量流量得到的压降与质量流量的关系。由图10可得:总压降随质量流量增大而增大,且呈单调递增特性。因此,可以判断螺旋管圈水冷壁在30%BMCR工况下的水动力不会发生多值性现象。

图10 螺旋管圈第149号管子的压降与质量流量关系
3.2 管子脉动校验
脉动是指管子或管屏的入口与出口流量周期性波动,且波动相位相差180°,大幅度脉动时进口流量的最低值可能大幅降低,甚至可能达到负值(即发生倒流)。
管子发生脉动的根本原因是蒸发受热面中蒸汽与水的比体积存在差异;外因主要是炉内热负荷突变,特别是蒸发开始区段热负荷的突变,造成局部压力突增。校验脉动应在最低负荷时进行,且应选取入口为欠热水、出口为汽水混合物或过热蒸汽的管子[18],因此选取30%BMCR工况下螺旋管圈受热最弱的第18号管子进行计算校验。采用动态蓄质量系数法[18]对脉动进行校验,校验结果见图11,计算得到管内动态蓄质量系数为0.985 6、阻力比为0.677 5,根据计算结果在图中画出A点。由图11可得:该管处于稳定区,且距离交界线有一定距离,认为管子不会发生脉动,且具有一定裕量。
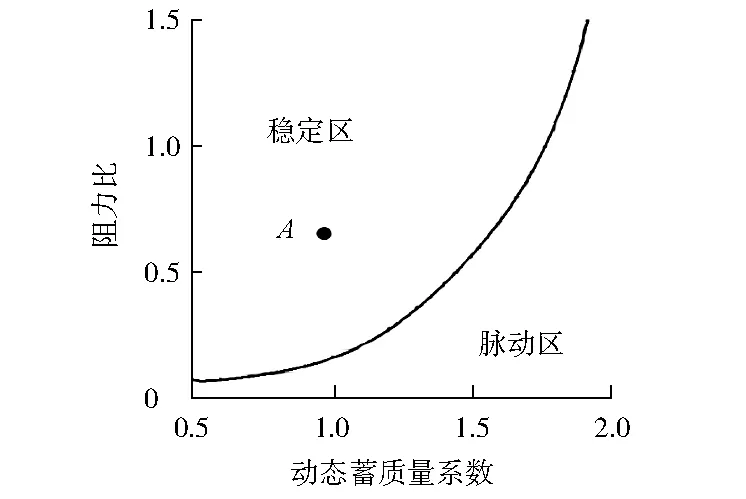
图11 动态蓄质量系数法校验螺旋管圈第18号管子脉动
4 结语
针对电站锅炉适应深度调峰时运行可行性问题,笔者以该650 MW超临界螺旋管圈水冷壁锅炉为对象,建立了水冷壁流量与压力节点的等效回路法计算模型、螺旋管圈水冷壁单管热负荷计算模型,并利用验证后的模型计算30%BMCR工况下的水冷壁水动力,从水动力多值性与管子脉动角度对超低负荷运行时的水冷壁安全性进行了校核,并得出以下结论:
(1)超低负荷下单根管子的水动力计算结果需要更高的准确度,笔者建立的水动力计算模型与螺旋管圈单管热负荷计算模型从理论角度能更好地确定水冷壁中每根管子的运行状况,可以提高水动力计算的准确性。
(2)30%BMCR工况水冷壁水动力计算结果表明超低负荷工况下,螺旋管圈出口外壁温度偏差比高负荷时更大,上下炉膛流量分配呈正响应特性,螺旋管圈质量流速偏差在低负荷时主要受结构不均的影响,垂直管路质量流速偏差主要受吸热不均的影响。
(3)通过水动力计算,采用动态蓄质量系数法对30%BMCR工况下的螺旋管圈水冷壁进行安全性校核,结果表明螺旋管圈单管呈水动力单值性,管子脉动处于稳定区且有较大裕量。
笔者对超临界锅炉水冷壁在超低负荷下水动力安全性进行分析评估,可为同类型机组适应深度调峰时的运行安全性分析提供依据。

