旋挖钻机桅杆瞬态动力学与疲劳研究
黄会荣,贺明辉,张 希
(1.西京学院 土木工程学院,陕西 西安 710123;2.西安建筑科技大学 机电工程学院,陕西 西安 710055;3.西安陕鼓动力股份有限公司,陕西 西安710075)
旋挖钻机作为一种灌注桩成孔的工程施工机械,因其操作简便,适应范围广,效率高、在注桩、连续墙、加固基础等多种地基基础施工中得到广泛应用[1].桅杆作为旋挖钻机的重要部件,在旋挖钻机入岩过程中承受多个外载荷作用,目前,国内外学者对截齿入岩的的载荷做了很多研究.李晓谷、姜丽丽等人基于硬岩条件下单个截齿的受力,建立了截割头载荷的数学模型,并通过模拟不同岩石的载荷,分析了截割头载荷特性及功率变化规律[2].罗春雷、丁吉等人根据岩石的物理特性、镐型截齿破岩的工作机理以及钻头的结构特征,分析了短螺旋钻头入岩的受载情况,并建立相应的载荷数学模型[3].王想等人通过建立载荷的数学模型对三种不同截齿布置参数的截割头破岩载荷进行了仿真[4].
通过分析文献[1-5],旋挖钻机入岩时的载荷与岩石类型、切削深度有关,如切削深度过大会降低旋挖钻机的使用寿命,过小会影响旋挖钻机作业效率.因此本文针对不同的组合岩石,根据钻头入岩时的载荷数学模型,通过模拟入岩时的载荷,同时确定切削深度的范围,然后将模拟得到的载荷应用到桅杆的瞬态动力学响应分析中,分析切削深度与桅杆应力之间的变化规律.
1 短螺旋入岩时模型的建立
1.1 钻头入岩时的载荷数学模型
短螺旋钻头钻进切削时,截齿切削的形式主要有平直切削与偏斜切削两种方式,前者为芯轴管截齿式,后者为引导叶片截齿式.通过对两种镐型不同的截齿型式进行分析,建立钻头钻进时载荷的数学模型.
因镐型截齿在钻进过程中所受的载荷具有很大的波动性,属于随机载荷.基于叠加理论,假设截割岩石时单齿随机载荷是载荷平均分量[5-7]与随机分量的叠加.本文将根据切削煤岩的相关理论、所选短螺旋钻头结构的相关参数,建立旋挖钻机钻进时所受载荷的数学模型.
由载荷的平均分量[7]与随机分量[8],获得了截齿在平直切削时所受的随机截割阻力Z″、随机牵引阻力Y″以及随机侧向阻力X″等三种阻力,分别为
Z″=[λσzkz[n]+
σk(kakbkc(0.25+0.018lh)+0.1Sd)]C
(1)
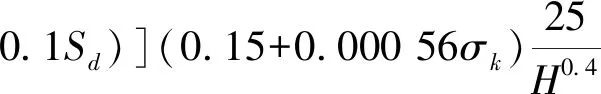
(2)
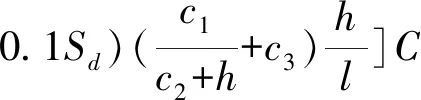
(3)
其中:
σz=0.523σk(σaσbσc(0.25+0.018lh)+0.1SLd)
ζ1[1]=η1[1],ζ2[1]=η2[1],ζ3[1]=η4[1]
式中:σk为岩石的接触强度,MPa;ka为截齿的齿形影响系数;kb为截齿的几何形状影响系数;对于文中的镐型截齿,则有kb=b1b2b3,b1、b2、b3为刀头形状影响系数、刀杆形状影响系数及刀头直径的影响系数;kc为截齿的切削角影响系数;l为相邻截线间的距离,mm;h为截齿的切削深度,mm;Sd为截割平面上的投影面积,mm2,对于镐型截齿一般取10~15 mm2;c1、c2、c3为截齿排列方式的影响系数;n为截齿载荷的模拟点数;σx、σy、σz为侧向阻力、牵引阻力以及截割阻力的均方差,MPa,其中,侧向阻力服从正态分布、牵引阻力服从Gamma分布、截割阻力服从瑞利分布;kx[n]、ky[n]、kz[n]为侧向阻力、牵引阻力以及截齿截割阻力的随机系数序列;C为截割岩石的修正系数;λ为载荷转换系数,λ=0为平均载荷,λ=1为随机载荷时.η1[1]、η2[1]、η3[1]、η4[1]为均值为0、标准差为1的独立正态随机数序列,ρ1[n]、ρ2[n]、ρ3[n]为(0,1)区间上均匀分布随机数序列,rzy为截割阻力与牵引阻力相关系数,Ag、Am为岩石、煤炭的抗切削强度,kg、km为岩石、煤炭的压出系数.
1.2 偏斜切削的载荷模型
动力头的扭矩会引起导向叶片产生偏斜切削,在钻进的极限状态下,假设短螺旋钻头上导向叶片的所有截齿都参与切削,则参与切削的截齿总轴向力Y1和总扭矩T1为
(4)
(5)
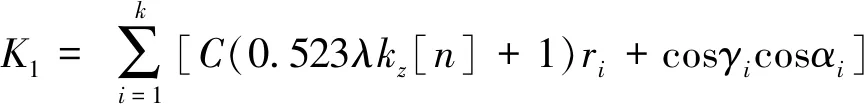
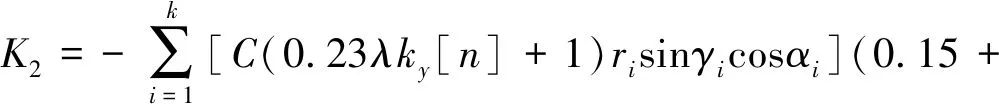
1.3 平直切削的载荷模型
假设短螺旋钻头的芯轴顶部截齿为平直切削,钻进时芯轴顶部截齿所受的总轴向力Y2和总扭矩T2为
(6)
(7)

1.4 钻头钻进的总载荷
根据短螺旋钻头结构与旋挖钻机的钻进原理,假设:(1)短螺旋钻头的径向力约等于零;(2)由于轴心线上的任意平面对布置在钻具上的截齿数都是对称的,故对附加钻头弯矩值的影响很小,可以忽略不计;(3)旋挖钻机往外输送碎屑的载荷与钻头切削岩石时的切削力相比很小,也可以忽略不计.因此,短螺旋钻头入岩时受到的载荷分为两部分,导向叶片产生偏斜切削产生的载荷、芯轴管顶部截齿的平直切削产生的载荷.通过求解,获得了钻头的总轴向载荷Y、总扭矩T
(8)
(9)
2 确定切削深度范围
2.1 确定旋挖钻机钻进时的最大切削[5]
从图1可以发现,模拟接触强度分别为800 MPa、650 MPa、490 MPa、350 MPa 的组合岩石,当对应的切削深度为22 mm、30 mm、40 mm、52 mm时,输出的扭矩峰值接近旋挖钻机最大扭矩,而轴向力峰值与旋挖钻机加压油缸的最大压力相比还有一些距离.模拟接触强度为1 000 MPa的岩石,对应的切削深度为16 mm时,输出的轴向力峰值接近旋挖钻机的最大加压力,扭矩峰值则有减小,但变化不大.
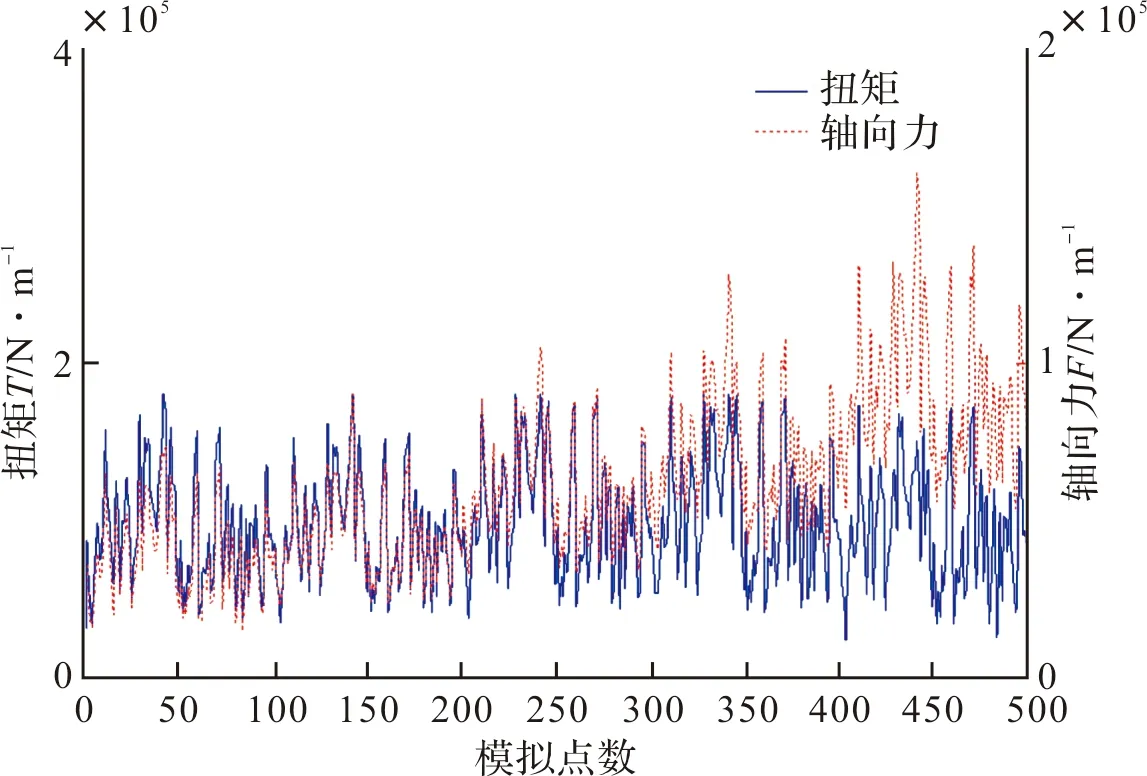
图1 组合岩石最大切削深度对应的载荷Fig.1 The load corresponding to the maximum cutting thickness of composite rock
2.2 确定旋挖钻机钻进时的最小切削深度[5]
当旋挖钻机在钻进过程中的切削深度达到某一数值时,旋挖钻机转速会达到其最大值.如果继续减小切削深度,其钻机的钻进效率降低.
为了提高钻机的工作效率,需保证旋挖钻机实际的转速不大于钻机设计转速的最大值,这样可以获得动力头在最大功率工作时其所对应的最小切削深度.最大功率下的钻机转速表达式为
(10)
式中,Pmax为动力头的最大功率;n为最大功率对应的钻进时的转速,r/min;η为钻进回转系统的总效率;T为钻头的总扭矩.
应用MTLAB模拟钻机的转速,得到该组合岩石的最小切削深度.
由图2所示,当组合岩石的切削深度为10 mm、13 mm、18 mm、22 mm、31 mm时,转速接近或达到旋挖钻机最大设计转速,由此可得,钻机的最小切削深度.组合岩石对应的切削深度的范围如表1所示.
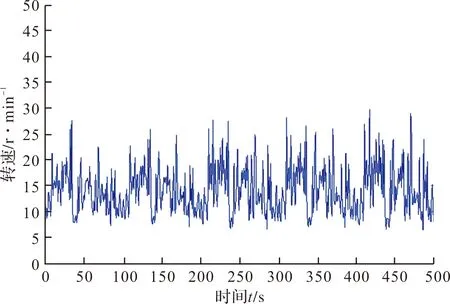
图2 组合岩石最小切削深度对应的转速Fig.2 Rotation speed corresponding to minimum cutting thickness of composite rock

表1 组合岩石对应的最大切削深度与最小切削深度Tab.1 Maximum cutting thickness and minimum cutting thickness of composite rock
3 桅杆瞬态动力学分析
当旋挖钻机处于钻进工况时,其所受的载荷为动载荷,所以通过动力头作用到桅杆上的载荷也为动载荷,通过瞬态动力学分析可以模拟出桅杆结构受到随时间变化的动载荷作用下的动力学响应[9].通过ANSYS的瞬态模块将模拟出的载荷以一定方式加载到桅杆上,求解得到桅杆危险部位的应力-时间历程[5].
本文对接触强度为1 000 MPa、800 MPa、650 MPa、490 MPa、350 MPa的组合岩石在四种不同切削深度下的工况进行瞬态响应分析,通过模拟得到了4种工况下的轴向力与扭矩,组合岩石对应的四种不同切削深度如表2所示.

表2 组合岩石对应的四种不同切削深度Tab.2 Four different cutting thicknesses corresponding to composite rock
3.1 桅杆有限元模型的建立
利用软件PRO/E建立与旋挖钻机桅杆实际尺寸相符的几何模型,适当简化对分析结果影响较小的部位.
单元类型:桅杆的瞬态分析选择的单元类型有SOLID92、SOLID95、BEAM188、LINK180单元.
材料属性:该旋挖钻机桅杆采用16Mn钢,其弹性模量为2.06e11 Pa,泊松比为7.85e6 kg/m3,材料密度为0.3.
划分网格:划分网格时,桅杆大部分区域单元尺寸为50 mm,其中桅杆与三角架、桅杆变幅油缸的铰接处、加压油缸支座及下桅杆导轨等受力较大的部位进行局部细化.整个桅杆划分后的网格单元数为282 985个,节点数为551 643个.
3.2 约束加载
约束:本文将旋挖钻机的桅杆结构单独进行瞬态分析,可将动臂变幅油缸、桅杆变幅油缸和底盘看作是刚性支撑,使用约束处理桅杆变幅油缸、三角架与桅杆之间铰接处的连接.考虑桅杆变幅油缸、三角架与桅杆之间铰接处为销轴连接,相互之间可绕轴转动,桅杆在建立有限元模型时采用的是三自由度(UX、UY、UZ)实体单元SOLID92和SOLID95,所以有必要对此进行处理.在对桅杆进行位移约束时采用改进的界面元法处理[10],即用梁单元BEAM188模拟销轴,用杆单元LINK180将轴套与销轴进行连接,可对销轴的轴向自由度进行释放.
加载:旋挖钻机入岩时桅杆受到的力主要是动力头作用到桅杆上扭矩T与加压油缸的反作用力F,将表2模拟得到的随机载荷以面力的形式将其施加到桅杆上,然后对其进行求解.
进入后处理,查看上述4种工况应力最大节点(103)的应力-时间历程,如图3所示.

图3 组合岩石不同切削深度的应力-时间历程Fig.3 Stress-time history of different cutting thickness of composite rock
由图4可得出,桅杆危险部位的应力随着旋挖钻机入岩时的切削深度减小而减小,并且当切削深度减小的幅度相同时,应力幅值减小的幅值逐渐减小.
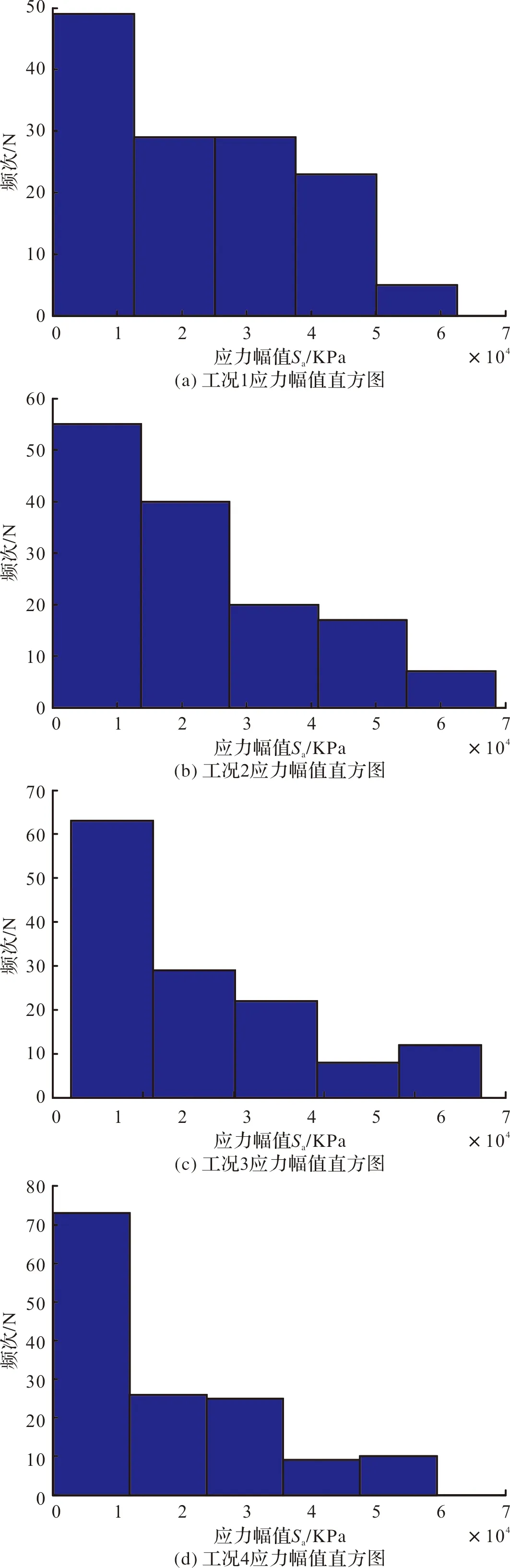
图4 工况1~4的应力幅值直方图Fig.4 Stress amplitude histogram of working condition 1~4
4 桅杆疲劳寿命分析
4.1 建立R-S-N曲线方程
本文中的旋挖钻机桅杆所采用的材料为Q355钢,基于损伤累积的疲劳寿命曲线可表示为
lgNR=aR+bRlgS
(11)
式中:aR和bR为存活率R下材料的疲劳参数;NR为存活率为R下的疲劳寿命.
由经验公式获得的材料平均应力为零,而结构在实际载荷谱下的平均应力不为零,为了解决该问题,利用古德曼(Goodman)公式求得对称循环载荷σ-1为
(12)
式中:σa为应力幅;σm为应力均值;σb为材料的强度极限.
通过抗疲劳设计手册[11],获得Q355钢的材料力学特性以及对称循环下的材料强度极限σb=586 MPa,存活率为50%时的R-S-N寿命曲线方程为
lgN=24.1-7.81lgδ-1
(13)
4.2 疲劳累积损伤理论
零件在交变载荷作用下产生的疲劳损伤过程称为疲劳破坏,线性累计损伤理论是经典的疲劳累积损伤理论之一.其在循环载荷作用下的应力是不相关的,它可以进行线性累加,直到累加值到达某一数值时构件就产生疲劳破坏[12].其中Miner理论被认为是线性理论中最典型的的理论.
疲劳损伤可写为
(14)
式中:ni为某一级的循环次数;Ni为某一级循环的疲劳寿命;r为循环级数;承受随机载荷结构的周期为
(15)
结构疲劳寿命为
(16)
根据式(16)与表7-表10获得了桅杆在钻进工况1-工况4的疲劳寿命N分别为1.820 8e+07、1.089 7e+07、6.695 4e+06、5.062 5e+06.
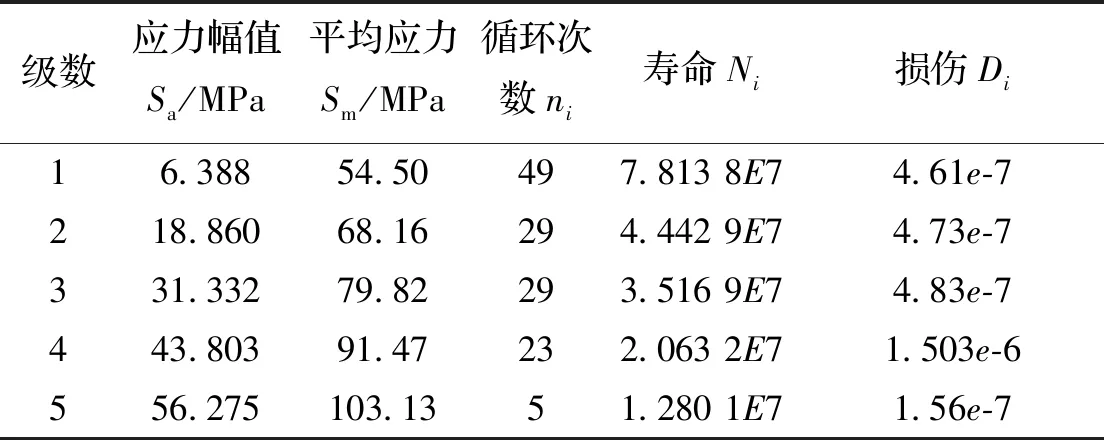
表7 桅杆在钻进工况1下的疲劳寿命估算Tab.7 Fatigue life estimation of guyed mast under working condition 1
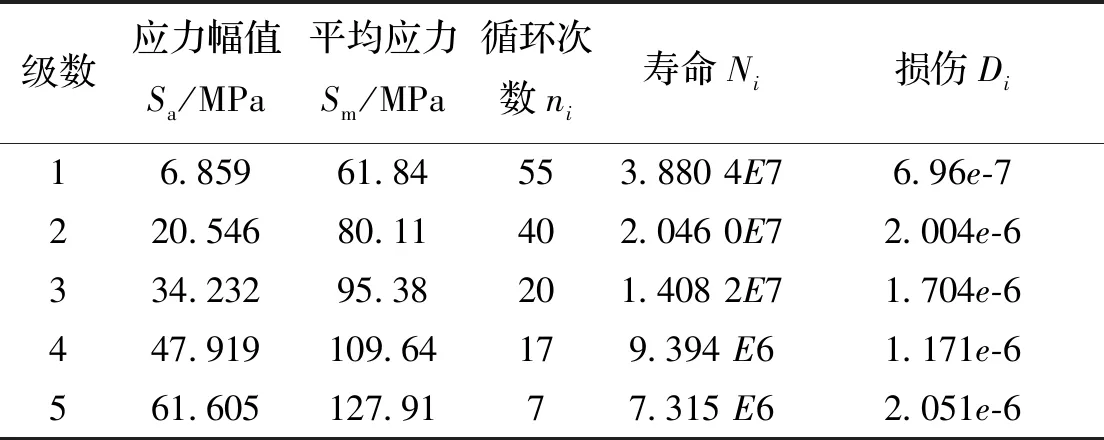
表8 桅杆在钻进工况2下的疲劳寿命估算Tab.8 Fatigue life estimation of guyed mast under 2 working condition 2
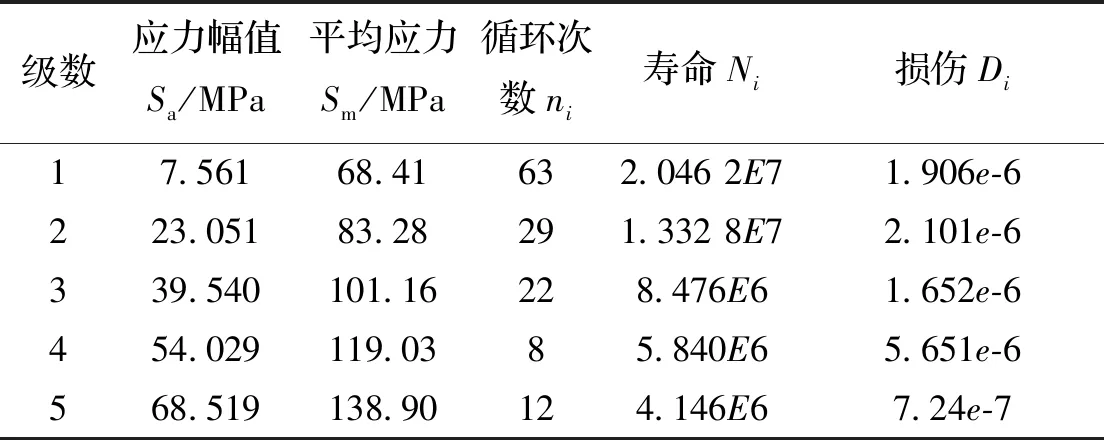
表9 桅杆在钻进工况3下的疲劳寿命估算Tab.9 Fatigue life estimation of guyed mast under working condition 3
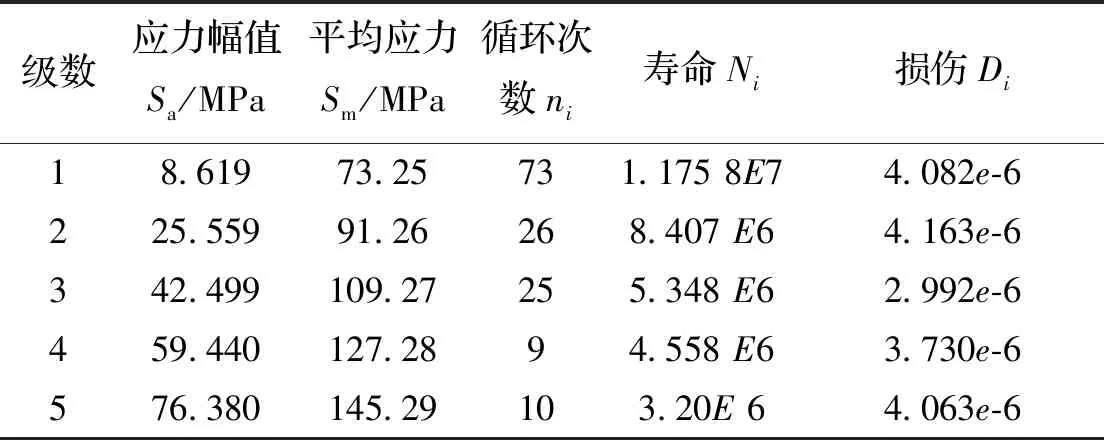
表10 桅杆在钻进工况4下的疲劳寿命估算Tab.10 Fatigue life estimation of guyed mast under working condition 4
计算结果分析:组合岩石的切削深度为10 mm、13 mm、18 mm、22 mm、31 mm时,桅杆危险部位的疲劳寿命为1.820 8e+07;切削深度为12 mm、16 mm、22 mm、28 mm、38 mm时,桅杆危险部位的疲劳寿命为1.089 7e+07;切削深度为14 mm、19 mm、26 mm、34 mm、45 mm时,桅杆危险部位的疲劳寿命为6.695 4e+06;切削深度为16 mm、22 mm、30 mm、40 mm、52 mm时,桅杆危险部位的疲劳寿命为5.062 5e+06.通过对上述计算结果的分析,可得出,在钻机入岩时切削深度允许的范围内,桅杆危险部位的疲劳寿命随切削深度的减小而增大,并且当切削深度减小的幅度相同时,桅杆危险部位疲劳寿命增加幅度的逐渐增大.
5 结论
(1)本文根据建立的钻头载荷的数学模型,利用MATLAB模拟了钻头钻进不同接触强度岩石的载荷情况,并根据旋挖钻机设计的最大扭矩与压力确定旋挖钻机入岩时的最大切削深度,由最大设计转速确定最小切削深度.可作为钻进时切削深度的参考,可避免因切削深度过大降低钻具寿命与因切削深度减小降低施工效率.
(2)通过模拟钻头入岩时的载荷,可以得出钻头钻进时的载荷特性,将所得载荷应用到桅杆瞬态分析中,通过对桅杆进行瞬态分析,可得到桅杆危险节点的应力情况,并揭示旋挖钻机桅杆危险部位的应力与随切削深度之间的关系,即桅杆应力随着旋挖钻机入岩时的切削深度减小而减小.
(3)通过计算得到表2中的组合岩石在四种不同切削深度下桅杆危险部位的疲劳寿命分别为1.820 8e+07、1.089 7e+07、6.695 4e+06、5.062 5e+06.结果表明,桅杆危险部位的疲劳寿命随着切削深度的减小而增大.当切削深度减小的幅度相同时,桅杆危险部位疲劳寿命增加幅度的逐渐增大.由此可知,选择一个合理的切削深度对提高桅杆的使用寿命高有着重要的意义.

