基于最大似然属性和拉普拉斯金字塔的断面波增强方法建立

张冰， 徐嘉亮* ， 王维红， 石颖， 王鹏

1 东北石油大学地球科学学院， 大庆 163318 2 油气资源与勘探技术教育部重点实验室(长江大学)， 武汉 430100

0 引言

断层及断裂构造对于改善储层物性、聚集成藏等具有重要作用，因此在有利勘探区开发过程中，断层的精细刻画与有效识别占有重要地位(徐嘉亮等，2018a；余博文，2021).在复杂断裂地区的勘探开发，由于受多期构造运动影响，断层较为发育，断层类型较多，在解释过程中对断层的识别和刻画的精细程度要求较高，就导致断层精细解释和断层平面组合变得更加困难(马玉歌等，2020；李海晨等，2020).随着地球物理及计算机相关技术的发展，断层识别技术取得较大进步，出现不同的断层识别方法.现在经过国内外学者的大量研究，已经形成较多断层识别方法，如沿层相干属性技术、相干体技术、方差体技术、曲率体属性、优势频带相位分析技术、蚂蚁追踪算法、边缘检测技术、面包切片技术等(Marfurt et al.，1998；Gersztenkorn and Marfurt，1999).相干体技术是现在使用最广泛的断层识别技术，第一代相干体技术(C1)主要利用互相关；第二代相干体技术(C2)是基于地震道相似性；第三代相干体技术(C3)是提取协方差矩阵的特征向量(Bahorich and Farmer，1995)；在此基础上又衍生出一些其他相干体技术.蚂蚁追踪算法是根据蚂蚁觅食行为而提出的断层自动识别技术(陈桂和刘洋，2021).边缘检测技术来源于图像处理，从最初应用到地震勘探领域到现在已经发展了较多的边缘检测技术，并在实际应用中取得较好的成果.Hale(2013)在研究断层扫描、提取断面和估算断距时提出最大似然属性，并在识别断层时效果较好.此外，在成像过程中断面波会在断层处成像，因此增强断面波能量可以在一定程度上对断层进行精细识别与刻画(徐嘉亮等，2015).

目前对于复杂构造断层及小尺度断层，利用识别度较高的断面波进行断层及断面解释是比较常用的方法(徐嘉亮等，2018b).如何提高断面波识别度，降低绕射波等干扰成为提高断面波识别度的关键(刘保金等，2012).本文利用断层识别度更高的大似然属性方法对断层进行了有效识别，并利用拉普拉斯金字塔增强方法对识别的断面波进行了增强，进而提高了断面波的识别度.通过在X地区进行本文方法应用，结果表明在地震剖面上断面波能量有所提高，得到更加清楚、连续性更好的断裂，断层组合关系更加清晰，取得较好的应用效果.

1 方法原理与关键步骤

1.1 最大似然属性原理

最大似然法是用统计方法建立一组区分函数，在多类别分析中计算出各个类别样本的归属概率，样本属于哪类由归属概率的大小决定(杨午阳，2017).

基于最大似然属性识别断层的原理源于对地震图像的相似性分析.Hale提出面向断面波的相似性理论，即应用矩形求取视窗中倾角和倾向的相似度.相似度属性由相似性通过构造导向平滑得到，相似性计算的基础是对地质体上沿反射界面不同方向变化率的估计，因此应先估计沿反射界面不同方向的反射斜率，然后进行最大似然属性计算.

1.1.1 估计反射斜率

计算反射斜率方法有很多，其中梯度结构张量(GST)是一种有效的方法在精确表征和分析地震数据中反射结构的特征上.其计算原理如下：

假设原始地震数据为S(x,y,t)，其复数域的解析信号可表示为

S(x,y,t)=s(x,y,t)+jsH(x,y,t)

=A(x,y,t)ejPhs(x,y,t)，

(1)

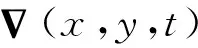
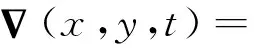
(2)

其梯度结构张量为：

(3)

其中w(x,y,t)为权重系数，表示对梯度向量的各个分量进行光滑平均，以达到对地震数据平滑滤波处理的目的.其表达式为：

(4)

式中：σ为噪声尺度参数，通常取值在0.1～3.0之间，x、y、t分别为地震数据中沿线方向、道方向和时间方向的变量.

经过平滑滤波后地震数据的梯度结构张量GST根据矩阵特征分解，可表示为：

GST(x,y,t)=

(5)

式中：λ1、λ2、λ3为梯度结构张量GST的特征值，且λ1>λ2>λ3>0，α1、α2、α3为梯度结构张量GST的特征值λ1、λ2、λ3对应的特征向量.即x、y方向的视倾角θx、θy可表示为：

(6)

(7)

式(6)和(7)的α1x(x,y,t)、α1y(x,y,t)、α1t(x,y,t)分别为式(5)中得到的最大特征值λ1对应的特征向量α1(x,y,t)分别在x、y和t方向上的三个分量.

1.1.2 相似性属性的计算

根据估计的反射斜率，由式(8)计算相似性：

(8)

式中：u为矩形方向窗口中的地震数据；K为矩形方向窗口中地震数据的道数；下标k表示时窗中第k道信号；xk、yk分别为第k道信号在x、y方向上的距离；θx、θy分别为x、y方向上的视倾角；θxxk+θyyk为第k道信号在时间轴的时移量.

然而，应用此方法计算的相似性，在分子和分母较小的地方会有很大变化.针对这种不稳定性需要进行相应的平滑处理，平滑处理后即得到相似属性.假设时窗大小为(2ω+1)ms，Z=ω/Δt，Δt表示采样率，此时式(8)可变为：

(9)

式(9)即为进行构造导向平滑处理后得到的计算稳定性增强的相似属性.

1.1.3 最大似然属性的计算

通过矩形方向窗口对断层倾角和倾向进行扫描得到的相似系数计算似然属性，如图1所示(以2D地震数据为例).假设断层倾角θ扫描范围为[θmaxmin]，扫描间隔为Δθ，断层倾向φ扫描范围为[φmaxmin]，扫描间隔为Δφ.在求取最大似然属性过程中，对于某一个采样点，分别对每一个扫描的倾角和倾向计算相似性，直到沿着相似度为最小值，即得到最大似然属性，公式为：

Maximun likelihood=max[1-semblance8].

(10)

由公式(10)可知，最大似然属性的数值范围在0～1之间.这样通过最大似然属性对断层及断裂的有效识别分析，就可以为解释断层提供更好的支持.

1.2 建立拉普拉斯金字塔增强原理

拉普拉斯金字塔增强是空域滤波能量增强中锐化滤波增强的一种，其主要是在图像的拉普拉斯金字塔分解过程中加入映射函数，得到由高斯金字塔演化而来的中间过程的拉普拉斯金字塔，最后得到需要的细节进行增强.

1.2.1 拉普拉斯金字塔分解

地震叠后数据的拉普拉斯金字塔构建是从高斯金字塔演变而来，因此首先应对地震信号进行高斯金字塔分解.假设原地震信号为F，并以原信号F作为高斯金字塔最底层地震信号G0；再对其进行低通滤波平滑和向下采样，常采用水平方向和垂向均为1/2，即得到高斯金字塔第一层；不断重复上述过程，就获得缩小尺寸的地震信号；层级越高，地震信号越小，从而构成高斯金字塔，其表达式为：

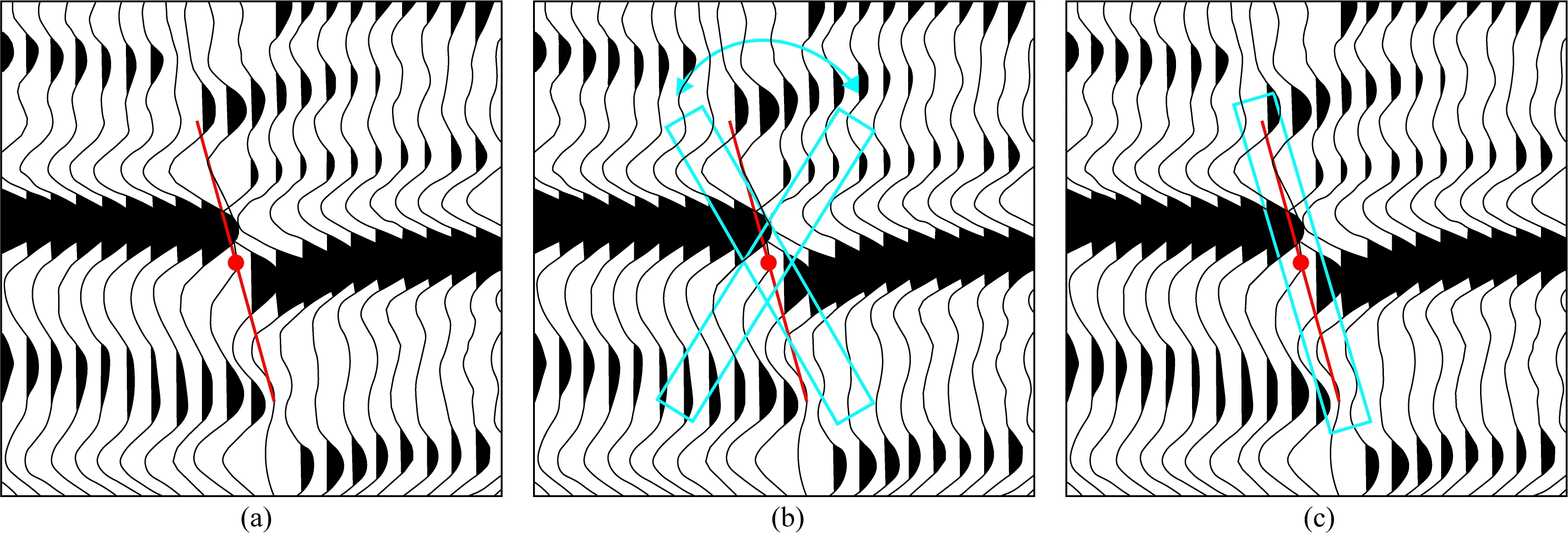
图1 最大似然属性计算示意图(a) 断面位置及采样点； (b) 扫描断面计算相似性； (c) 最小相似性对应位置.Fig.1 Schematic diagram of maximum likelihood attribute calculation(a) Section position and sampling point; (b) Similarity of scanning section calculation; (c) Minimum similarity corresponding position.

(11)

式中：N为层数；Rl为高斯金字塔第l层的行数；Cl为高斯金字塔第l层的列数；ω(m,n)是5×5的二维高斯内核，其表达式为：

(12)

ω(m,n)实际是高斯低通滤波器,经过n次重复之后得到Gn，此时Gn只包含级少数的像素点.

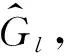
1≤l≤N,0≤i≤Rl,0≤j≤Cl，

(13)

式中：N为层数；ω(m,n)是5×5的二维高斯内核.拉普拉斯金字塔第l层地震信号Ll表达式为：

(14)

通过对地震信号的拉普拉斯金字塔分解，可以把原地震信号分解到不同的空间频带上，根据需要对相应的细节进行增强，如图2所示.通过拉普拉斯金字塔也可对增强后的地震信号进行重建，其表达式为：

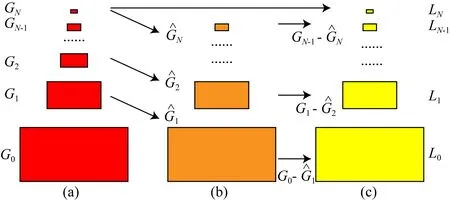
图2 构造过程(a) 高斯金字塔； (b) 对高斯金字塔进行变换； (c) 拉普拉斯金字塔.Fig.2 Construction process(a) Gaussian pyramid; (b) Transform of Gaussian pyramid; (c) Laplace pyramid.

(15)

当l=0时，得到重建后地震信号，假如在变换过程中没有做相关参数修改，得到的重建信号与原始地震信号完全相同.

1.2.2 地震数据的重映射

在对地震剖面进行初始变化时，首先假设一个能量参数ε，如果地震剖面断面部分的能量变化小于ε，就认为是细节部分，如果大于ε，就认为是边缘部分.在重映射算法中，当计算输出金字塔系数时，某点强度(强度是指单通道像素值的大小)可表示为g0=Gl0(x0,y0).在构建拉普拉斯金字塔过程中地震断面波能量在ε附近的被认为是细节处理，其表达式为：

φd(i)=g0+sign(i-g0)εfd(|i-g0|/ε)，

(16)

式中：g0为当前要处理的像素点；sign(i-g0)为亮度差异(i-g0)的符号值；ε可通过限定细节部分像素点的个数≤nd来确定当前层中ε的值；fd(x)=ex是映射函数，用于控制增强细节部分；|i-g0|为像素点i与数据周围像素点的差异值；下标d表示细节detail的首字母.

对重映射处理后的地震剖面构造其拉普拉斯金字塔，然后再对增强后的地震剖面进行重建，即可得到断面波能量增强的地震剖面，有利于后续的断层解释与有利圈闭的识别.

1.3 关键步骤

在实际应用过程中，通过最大似然属性进行断裂识别和拉普拉斯金字塔断面增强包括以下步骤：

1.3.1 断裂特征分析与成像加强

通过对工区内地震数据的分析，明确目的层内断裂构造在地震上的反射特征.了解工区的构造发育史，和断裂形成的时期，以及断裂特征类型，以便于后续相关参数的合理选择.

最大似然属性断裂识别和拉普拉斯金字塔增强断面的理论基础仍然是在地震剖面上反射波同相轴的不连续性，噪声、较低的分辨率和地层岩性的突然变化也可能导致反射波同相轴不连续，因此在地震数据处理过程中要注重叠前相关噪声的有效压制和提高地震数据的分辨率，在Kirchhoff 叠前时间偏移过程中，要注重偏移孔径和反假频因子的合理选择，在偏移成像后通过随机噪声压制和叠后提高分辨率处理技术，来进一步提高断面波成像效果.

1.3.2 最大似然属性断裂识别

最大似然属性原理在上文中已经叙述，从地震数据体中计算最大似然属性时，有两个关键参数：矩形窗口的水平计算因子、垂直计算因子.水平计算因子和垂直计算因子越大，计算周期越长，计算出最大似然属性连续性越好.

1.3.3 拉普拉斯金字塔增强断面

根据最大似然属性对断层的识别，通过拉普拉斯金字塔进行断面增强，首先对地震信号进行高斯金字塔搭建，再通过从每一层减去高斯金字塔上一层信号且进行内核卷积的地震信号，就得到拉普拉斯金字塔，在搭建拉普拉斯金字塔过程中加入一个映射函数来增强断面部分，并用拉普拉斯金字塔对地震信号进行重建，即得到断面增强后的地震数据.

2 模型试算

本文以图3所示的带有两条断层的四层速度模型进行方法测试.该模型在水平和垂直方向上分别有500个网格点，网格间距为2 m，炮间距为20 m，每炮共有400个检波器接收记录.第一炮与最后一炮的位置分别在200 m和800 m的位置.该观测系统能够保证左侧断层满覆盖接收，右侧断裂不满覆盖接收，进而验证在满覆盖与不满覆盖情况下本文方法的实用性.

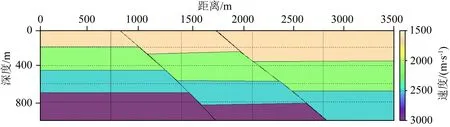
图3 带有两条断层的正演速度模型Fig.3 Forward velocity model with two faults

由于正演模型断层倾角较大，断面波能量较低.图4a为Kirchhoff叠前时间偏移原始剖面，图4b为利用本文方法增强断层后的叠前时间偏移剖面，两条断层能量均有所增强，连续性变好且识别度变高，更有助于利用断面波进行断层解释.

3 实际应用对比

本文将最大似然属性和拉普拉斯金字塔增强在X地区进行应用，并取得较好效果.X地区主控及分支断层在剖面上组合成花状构造、阶梯状构造和反Y字型构造，同时还伴有一些小的走滑断裂.在原叠加剖面上这些构造位置关系不明确，造成断层解释和平面组合困难.此外，由于河道交错叠置复杂，河道边界的异常响应也干扰断层识别.为落实断层解释，采用最大似然属性识别断层和拉普拉斯金字塔增强断面，并取得一定效果.图5a为增强前测线A的偏移剖面，断面处连续性较差且断层搭接关系不明确，且存在假断层响应影响断层解释精度，图5b是增强后测线A的叠加剖面，断面波能量有所增强，断层连续性较好且搭接关系明确.图6a和图6b为图5断层增强前后剖面的局部方法，由局部放大比较中能够明显看出利用本文提出的方法能够增强断面波的能量，进而提高断层的识别度.

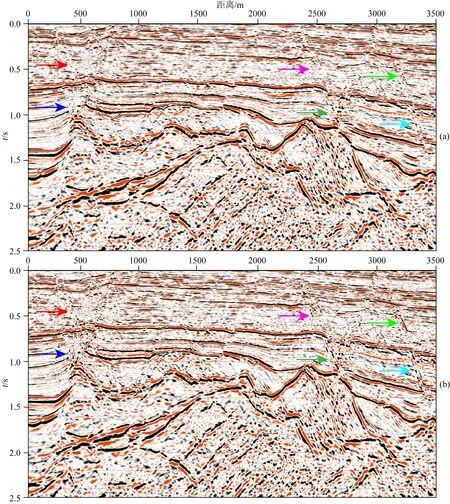
图5 增强前后测线A的叠加剖面对比(a) 原始叠加剖面； (b) 增强后叠加剖面.Fig.5 Comparison of stacked profiles A before and after enhancement(a) Original section； (b) Enhanced section.

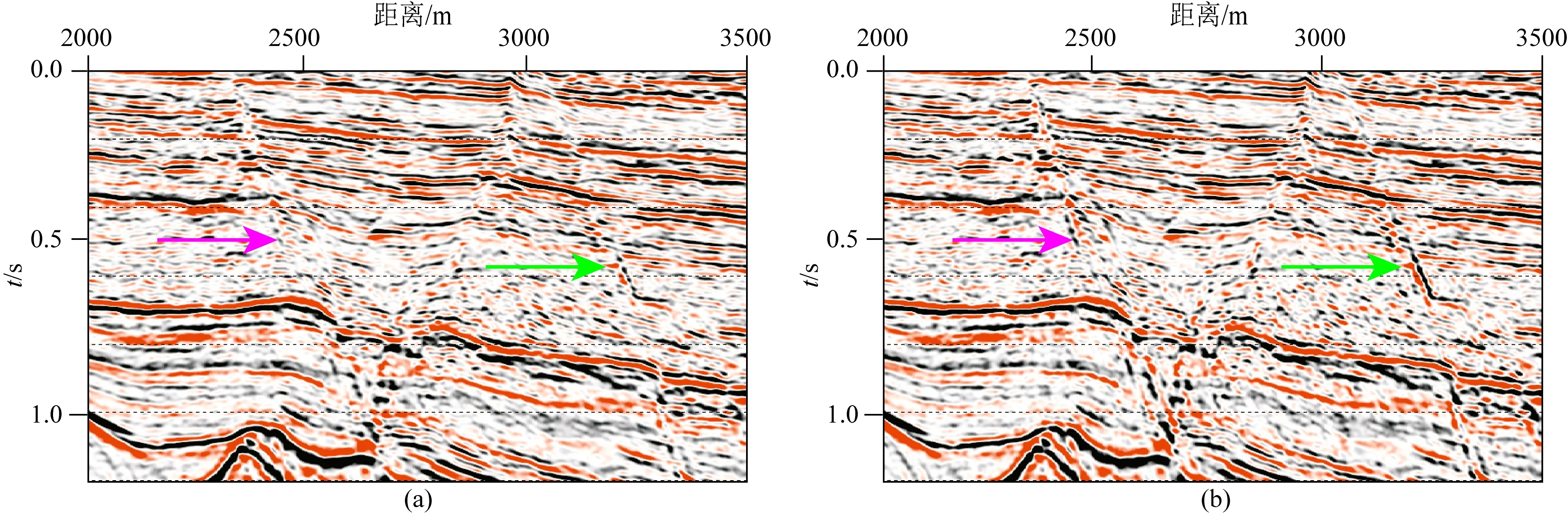
图6 增强前后测线A的叠加剖面对比(a) 原始叠加剖面； (b) 增强后叠加剖面.Fig.6 Comparison of stacked profile A before and after enhancement(a) Original section； (b) Enhanced section.

图7和图8是对测线B叠前时间偏移剖面的增强及其布局方法的比较，可看到增强前后断面波能量明显提高，断层连续性较好且搭接关系更明确.

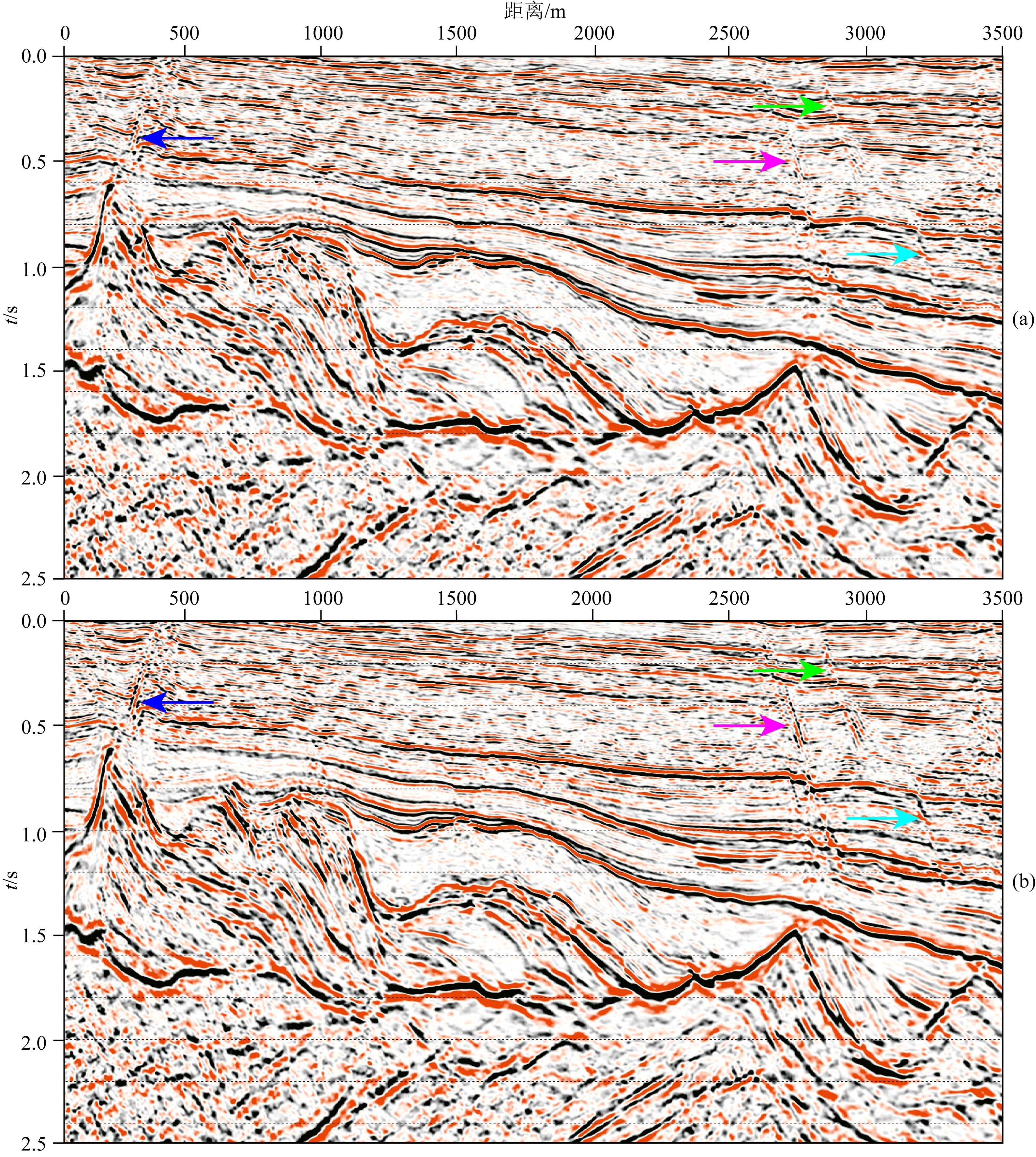
图7 增强前后测线B的叠加剖面对比(a) 原始叠加剖面； (b) 增强后叠加剖面.Fig.7 Comparison of stacked profile B before and after enhancement(a) Original section； (b) Enhanced section.

图8 增强前后测线B的叠加剖面对比(a) 原始叠加剖面； (b) 增强后叠加剖面.Fig.8 Comparison of stacked profile B before and after enhancement(a) Original section； (b) Enhanced section.

图9a为该区T2(馆陶组)层段常规相干体水平切片，可以发现X地区主断裂为近东西向展布，但该相干体横向分辨能力较低，断层边界模糊影响其真实性.图9b表示断面波照明度增强后最大似然水平切片，最大似然体横向分辨能力较高，次级断裂与主断裂的接触关系较清楚，断层细节更加清楚、连续，且刻画断层边界更加清晰，断层组合关系明确，有利于断层识别，更加符合断裂的实际地质特征.

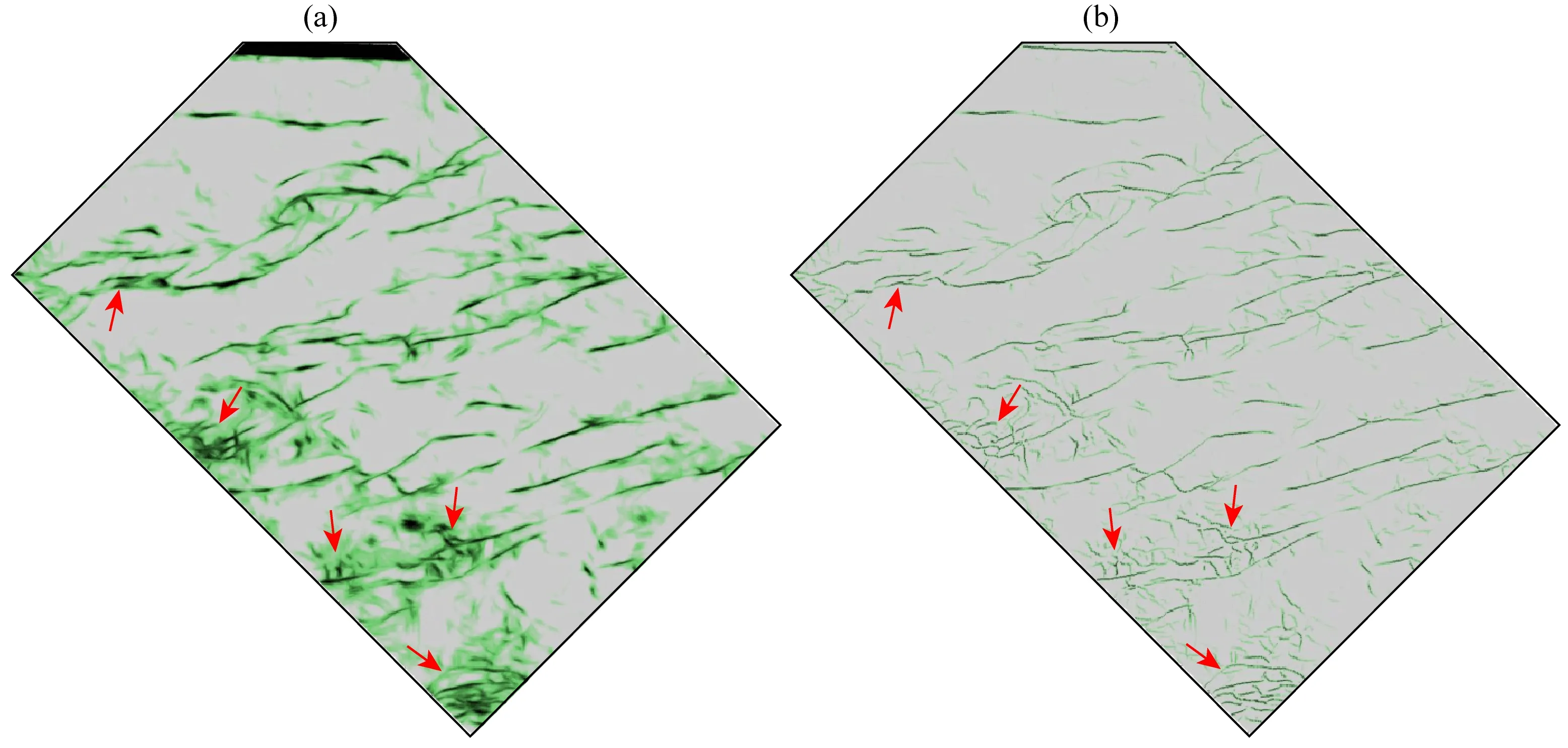
图9 X地区地震资料平面分析(a) 常规相干体水平切片； (b) 断面波照明度增强后相干体水平切片.Fig.9 X area seismic data plane analysis(a) Horizontal slice of conventional coherent body； (b) Horizontal slice of coherent body after enhancing fault-surface wave illumination.

4 讨论及结论

通过分析最大似然属性识别断层和基于拉普拉斯金字塔算法增强断面识别度的原理，以及在X地区的应用，与直接应用常规地震资料对断层精细解释和识别相比，应用此方法，可以显著提高断面波在叠加剖面上的振幅能量，有利于后续分析断层位置以及断层展布特征、断层平面组合关系，较好地实现断层精细解释和断裂系统的有效识别.然而在最大似然属性识别断裂时，要注意矩形窗口的水平计算因子、垂直计算因子的合理选择，保证运算时间的合理性，且计算的最大似然属性具有较好的连续性，同时，在研究中发现最大似然属性在某些高振幅的地质体边界处仍具有一定异常响应，影响断层识别，需要进一步改善提高.此外在基于拉普拉斯金字塔算法增强断面时，由于地震图像中存在与断面部分强度变化相似的异常响应，在拉普拉斯金字塔算法增强断面时异常相应也会得到增强，对于该算法的不足之处，还需要针对原地震剖面中断层的特点进行改进，以获得更好的断面增强效果.

本文分析了最大似然属性识别断层和基于拉普拉斯金字塔算法增强断面的原理，并在X地区进行应用，即通过最大似然属性对工区数据体进行扫描，并计算数据体采样点之间的相似性，以获得工区内最可能发育断层的位置及概率，然后应用拉普拉斯金字塔增强算法进行断面增强，即在构造拉普拉斯金字塔的过程中加入一个映射函数，使断面得到增强.在X地区的实际应用表明，最大似然属性在叠加剖面上识别断层位置比较准确，再通过拉普拉斯金字塔算法增强断面，可得到断面波能量较高的叠加剖面，在剖面上断层平面组合关系更明确，提高了断层解释精度，为后续有利圈闭识别和井位优选提供了依据.