基于IITD模糊熵与随机森林的滚动轴承故障诊断方法
陈 剑,蔡坤奇,陶善勇,杨 斌,刘圆圆,刘幸福,黄凯旋
(1.合肥工业大学 噪声振动研究所,安徽 合肥 230009;2.安徽省汽车NVH技术研究中心,安徽 合肥 230009)
1 引 言
滚动轴承是大多数机械和电气设备的重要支承部件,它发生故障将直接影响设备的正常工作,导致重大经济损失。准确有效地轴承故障诊断既可提高设备运行的可靠性和稳定性,也可避免重大事故的发生[1]。
滚动轴承故障诊断主要包括两个方面,故障特征提取和故障模式识别。通常,故障特征提取可进行时域特征、频域特征或者时频特征分析,进而构建特征向量。对于非平稳、非线性信号,时频分析是最有效的分析方法。常见的滚动轴承故障时频提取方法有:局部均值分解、经验模态分解、变分模态分解、小波变换、固有时间尺度分解等[2,3]。故障模式识别是人工智能研究领域的一个重要研究方向,基于系统论、控制论和信息论,主要研究参数估计、系统辨识等。常见方法有:神经网络、聚类分析和支持向量机方法等[4,5,15]。
固有时间尺度分解(intrinsic time scale decomposition,ITD)是Frei M G等人提出的一种自适应时频分析方法[6],相比经验模态分解(empirical mode decomposition,EMD)和局部均值分解(local mean decomposition,LMD),ITD方法在端点效应和计算效率方面优势明显,且适合在线监测和分解[7]。但ITD方法自身也存在一些不足,即采用线性变换构造基线号有可能导致分解后的信号出现毛刺而失真;IITD(improved intrinsic time scale decomposition)方法改善了ITD分解的波形失真和端点效应问题,广泛应用于故障诊断领域[8,9]。文献[10]提出基于固有时间尺度分解和近似熵结合随机森林(RF)的轴承故障诊断方法,虽提高了微弱信号故障诊断准确率,但近似熵采用硬阈值判据指标,影响数据统计结果稳定性。文献[11]提出基于IITD样本熵和支持向量机的齿轮故障诊断方法,但样本熵易受数据波动影响,支持向量机在处理大样本数据能力不足以及多分类问题精度较低等缺陷。
本文拟将IITD分解和模糊熵方法用于滚动轴承振动故障信号特征提取,构建其特征向量,作为随机森林分类器的输入用于轴承故障类型识别与诊断,以解决近似熵和样本熵易受数据波动,支持向量机处理大样本数据能力不足等问题。其主要原理是:对原振动信号进行IITD分解得到多个PR分量,提取PR分量的模糊熵构建特征向量来表达故障轴承的信号特征;然后采用随机森林算法对轴承故障进行模式识别分类,最后与支持向量机识别结果对比,验证方法的准确性和优越性。
2 基于IITD和模糊熵的滚动轴承特征提取方法
2.1 IITD方法
ITD分解的分量出现明显变形和端点效应,对原信号分解精度产生影响,进而导致各PR分量发生改变且分解得到的信号左、右两端伪局部极值点。IITD分解,采用端点延拓和三次样条拟合的方法,使IITD分解后的分量更精准地体现原始信号的频率成分。
IITD分解具体步骤如下[12]:
1) 确定信号Xt(t≥0)的局部极值点XN对应的时刻τk(k=1,2,…,N),N为极值点的个数,在连续极值点[τk,τk+1]上,定义信号线性提取因子L为:
(1)
式中:
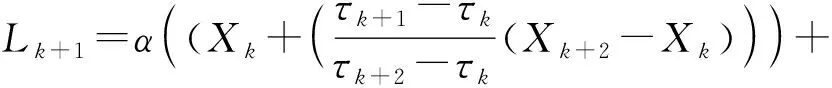
式中:α为线性缩放因子,一般取值为0.5。
2) 上述公式提取到的基线控制点Lk,通过对时间序列采用镜像对称延拓方法,可得左右两端极值点(τ0,X0),(τM+1,XM+1),令k分别为0和M-1进而求出L1与LM的值,再用三次样条插值函数拟合得到基线信号L1(t)。
3) 原信号Xt与基线信号Lt之差得到固有旋转因子h1(t):
h1(t)=Xt-L1(t)
(2)
判断基线Lk+1≠0,则h1(t)是一个固有旋转分量,输出h1(t),令PR1=h1(t),如果Lk+1=0,则h1(t)作为原始数据,重复上述步骤直到满足:
h1k(t)=PR1
(3)
4) 从原始数据中分离出来PR1分量,得到新信号r1(t),具体过程为:
r1(t)=Xt-PR1
(4)
5) 将r1(t)作为新的给定信号重复步骤(1)~(4),循环n-1次之后,直到将rn(t)为一单调函数或常函数,最终,原始信号Xt被分解为n个PR分量和一个残余项r1(t)之和。
(5)
2.2 IITD和ITD的对比分析
为了验证IITD分解信号的有效性,分别采用IITD、ITD方法对一解析信号进行分解。设仿真信号为:x1=(1+0.5cos(8 π t))·cos(200 π t+2cos(10 π t)),x2=cos(30 π t),x=x1+x2,采样频率为1 kHz,采样点数为1 000。3种方法的分解结果分别如图1、图2、图3所示。
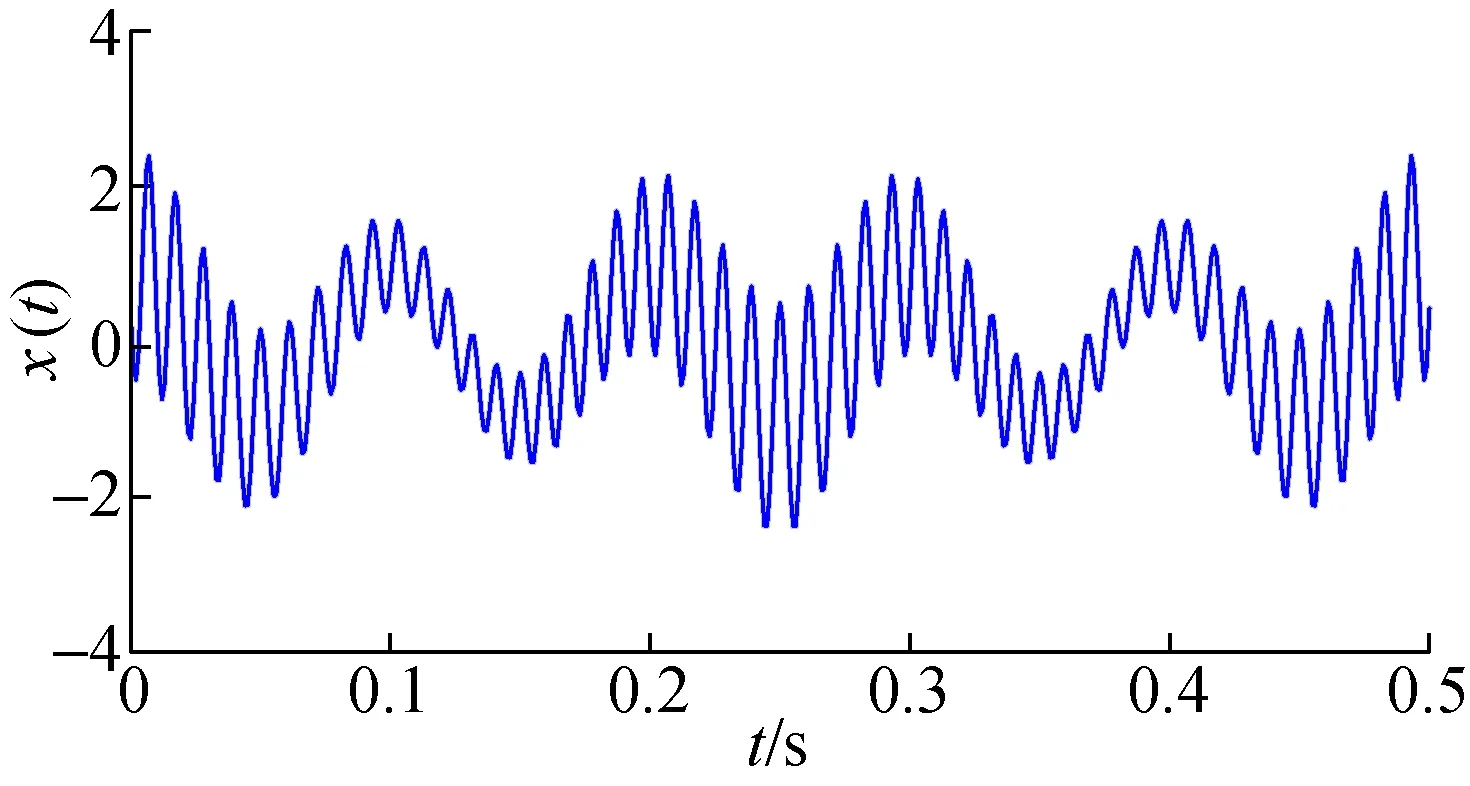
图1 仿真信号波形图Fig.1 Simulation signal waveform
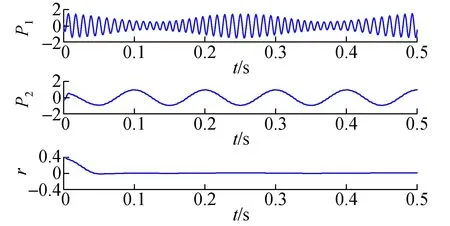
图2 信号x(t) ITD分解结果Fig.2 ITD decomposition result of signal x(t)

图3 信号x(t) IITD分解结果Fig.3 IITD decomposition results of signal x(t)
比较二者的分解结果,从图2、图3分解的分量效果表明,ITD分解得到的第二个分量出现了明显的端点效应,IITD分解得到的分量较ITD光滑,更准确地体现仿真信号的频率组成。
2.3 模糊熵
模糊熵是由Zadeh L A在1968年首次提出,它用来描述一个模糊集模糊程度[13]。采用近似熵和样本熵处理信号时,信号的绝对幅值差决定其相似性,数据的波动对结果产生影响。模糊熵算法则通过均值运算,采用指数函数代替绝对幅值差,除去基线漂移和数据波动的影响,向量的相似度由模糊函数形状决定,保证模糊熵值随参数平稳变化。
模糊熵的定义为:
1) 对于给定的N点时间序列{u(i):1≤i≤N},处理后得到m维向量:
(6)
(7)
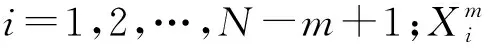
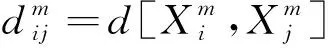
(u(i+k)-u0(j))|)
(8)
i,j=1,2…N-m;i≠j
(9)
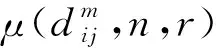
4) 定义函数:
(10)
5) 同样,根据以上步骤构造m+1维向量:
(11)
6) 定义模糊熵为:
FuzzyEn(m,n,r)=
(12)
当N为有限数时,上述表达为:
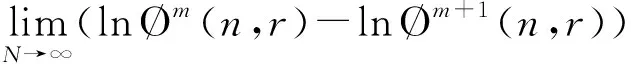
(13)
上述公式中,模糊熵的值不仅与数据长度N有关,还与参数m、r和n有关。根据文献[14]的研究,嵌入维数m一般选择1或2,模糊函数的梯度n,相似容限r取0.1~0.5 SD(SD是原数据的标准差),本文计算取值:N取2 048,n取2,m取2,r取0.2 SD。
3 基于随机森林的模式识别
3.1 随机森林原理
随机森林(random forest)是Breiman在2001年提出的一种分类方法,采用Bagging技术训练多个决策树组合得到随机森林。基于Bagging算法,随机森林同时加入了样本和特征两个方面的随机属性选择。随机森林分类的思想是随机选择一些特征属性构建一个决策树,重复这个过程建立多个决策树,并由产生的决策树作为投票原则产生分类结果。
3.2 随机森林的算法过程
1) 生成每颗决策树的训练集。随机森林利用Bootstrap法重采样从原始训练集中有放回无权重地抽取T个训练子集,每一个子集对应一个决策树。未被抽中的数据称为袋外OOB(out-of-bag)数据,OOB数据用来评估分类器的正确率,且对异常数据具有抗干扰能力,这样可以避免随机森林中的决策树产生局部最优解,使分类更准确。
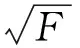
3) 特征β把节点分成2个分支,然后从剩下的特征中寻找分类效果最好的特征,最终决策树按照不纯度最小原则充分生长,且不剪枝处理,直到决策树的属性生长到叶子节点或完全被使用。
4) 通过构建的决策树对测试样本预测后分类,分类的标签来自于所有决策树的综合。基于IITD模糊熵的随机森林模式识别具体方法如图4所示。
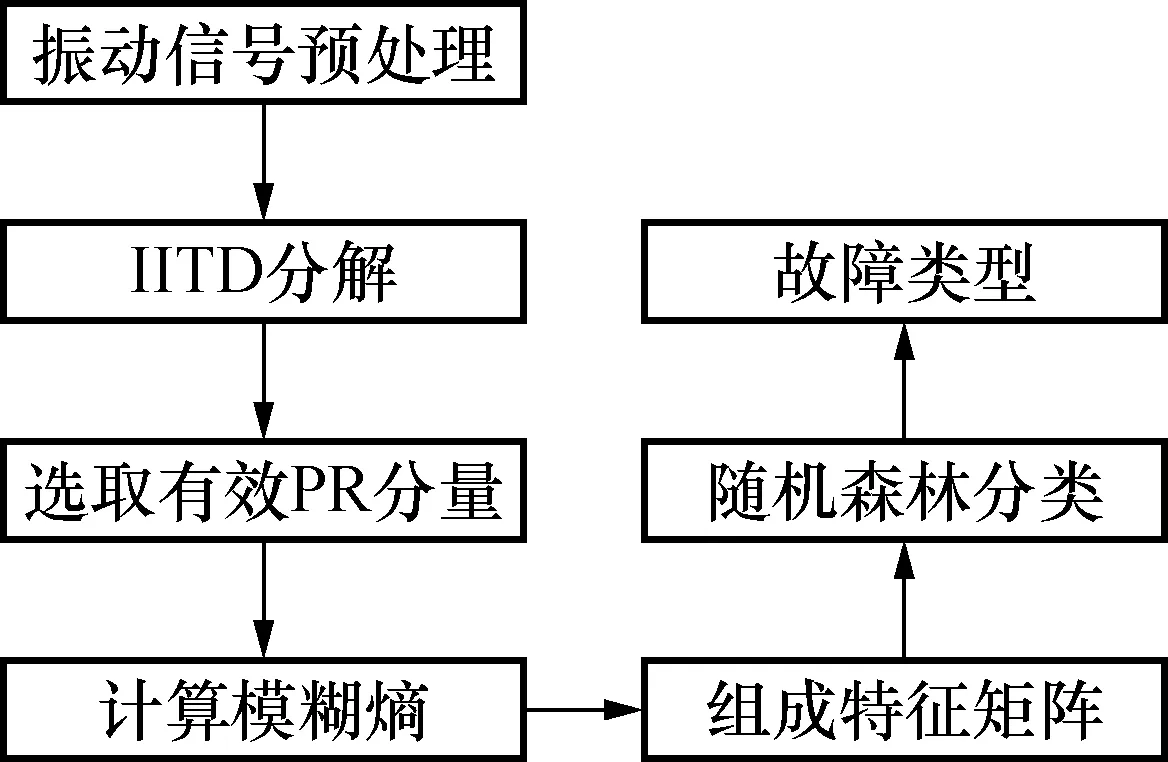
图4 基于IITD模糊熵和RF的滚动轴承诊断方法Fig.4 Diagnosis method of rolling bearing based on IITD fuzzy entropy and RF
4 实验分析
4.1 数据来源
实验数据来自合肥工业大学航空发动机轴承试验台。试验台的整体结构布置如图5所示。实验轴承采用NSK的NU1010型号单列圆柱滚子轴承。为满足实验需求,利用激光打标机和线切割加工出内圈、外圈、滚动体等3种轴承故障。

图5 轴承试验台总体结构Fig.5 Overall structure of bearing test bench
利用LMS Test.lab软件在电脑上采集额定轴向载荷等4种故障状态3种转速振动信号,传感器测点布置如图6所示。试验工况设定:采样频率为20 480 Hz。转速为3 000 rpm,轴向载荷为2 kN,定转速每类故障状态采集长度为634 880。

图6 传感器测点布置Fig.6 Sensor measuring point arrangement
4.2 数据验证
随机选取45组长度为1 000个采样点的样本,其中随机选择30组作为训练,另外15组用来测试。IITD分解得到前5个PR分量与原信号Xt之间相关度高于设定阈值λ=0.2,相关性较高; 第6个分量相关性为0.023,远小于0.2,故选取前5个PR分量进行计算得到模糊熵数据。4种故障状态经过计算,最终形成(4×45)×5即维数为180×5的数据集。
随机抽取120组训练集数据训练得到随机森林分类器模型。剩余60组测试集数据用来验证。为了体现随机森林分类方法的准确性,使用模糊熵数据集训练SVM、BPNN对比。三者分类输出结果分别如图7(a)、(b)、(c)和表1所示。其中图7中纵坐标类别标签1、2、3、4分别对应轴承的滚子故障、内圈故障、外圈故障、正常状态。
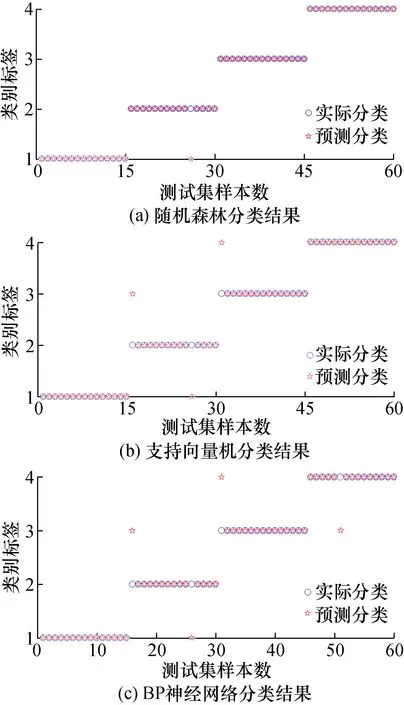
图7 RF、SVM与BPNN分类结果对比Fig.7 Comparison of classification results of RF, SVM and BPNN
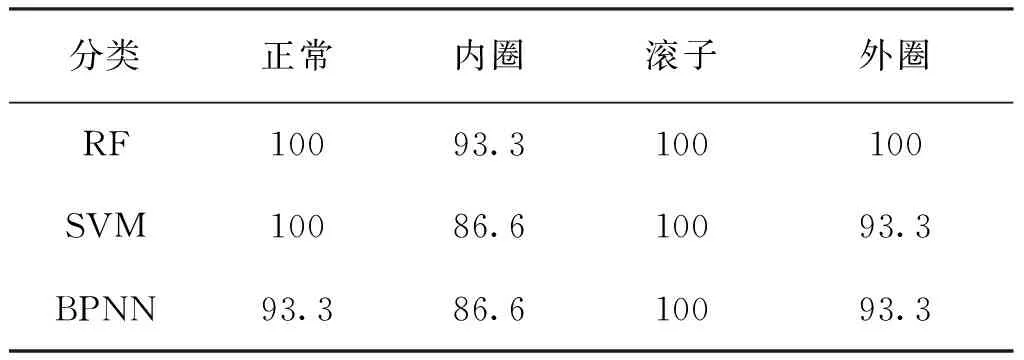
表1 随机森林和支持向量机诊断准确率对比Tab.1 Comparison of diagnosis accuracy between random forest and support vector machine (%)
针对IITD分解得到模糊熵数据构成的特征向量,IITD-RF方法识别率最高,误判数为1次;IITD-SVM以及IITD-BPNN方法误判次数分别为3次和4次。由表1可以看出IITD模糊熵与随机森林的滚动轴承故障诊断方法准确率高于其余两种,对滚动轴承故障诊断更有优势。
5 结 论
本文提出了一种将IITD与模糊熵结合并利用随机森林分类的滚动轴承故障诊断方法。IITD方法克服了ITD的缺点,分解得到的分量曲线光滑;模糊熵应用到滚动轴承故障诊断,消除了数据波动的影响;采用随机森林和支持向量机、BP神经网络等3种算法对故障轴承进行模式识别,实验对比结果表明,本文方法能准确地诊断出滚动轴承的故障类型,且分类总精度大于98%,验证了该方法的有效性,为滚动轴承故障诊断提供了新思路。

