盾构掘进过程离散元仿真与交互作用分析

赵卫星，管会生，廖 江

(1. 中铁建昆仑地铁投资建设管理有限公司，四川 成都 610040； 2. 西南交通大学机械工程学院，四川 成都 610031)

0 引言

成都砂卵石地层由于自稳性差、卵砾石含量高等特点，给地铁盾构法施工增加不少困难，盾构施工经常会遇到刀盘卡停、中心结泥饼、刀盘过度磨损以及螺旋输送机断轴等问题[1-4]； 盾构掘进过程中无法直观观察土体的运动状态，从而无法采取有效的解决措施。因此，对砂卵石地层下盾构掘进过程进行研究，对于解决砂卵石地层下盾构施工难题具有重要意义。

目前，对盾构掘进过程的研究大多采用的是有限元方法、缩小模型试验法以及离散元法。苏翠侠等[5]利用有限元理论及相关软件，对刀盘掘进过程进行三维动态数值模拟，分析了刀盘力学特性及参数的变化规律； 杨果林等[6]基于实际工程数据，研究了贯入度、场切入指数和掘进比能三者间的变化关系，并讨论了地层的可掘性问题； 王俊等[7]开展了室内掘进试验，探究了砂卵石地层中土压盾构隧道掌子面失稳诱发地层变形的特征，同时通过三维离散元仿真研究隧道埋深对掌子面稳定性的影响规律。

目前针对盾构掘进过程的研究基本集中于刀盘的力学特性和参数变化规律等方面，几乎没有针对螺旋输送机力学特性的研究，针对卵石土力学响应和运动规律的研究也涉及较少。由于砂卵石地层的特殊性，采用离散元方法进行分析能更准确地反映砂卵石土体的运动规律。因此，本文基于离散元理论和分析方法，建立砂卵石土体从掘进到排出的盾构掘进过程仿真模型，对盾构掘进过程中土体的运动规律和受力特征进行研究，并对刀盘和螺旋输送机进行分析，从而解决刀盘切削、排渣过程难以可视化，卵石颗粒流动性难以定量分析的难题。

1 工程地质概况

1.1 总体概况与地质构造

成都地铁6号线一、二期工程3标尚锦路—红高路站区间(以下简称尚红区间)右线起点里程为 YDK8+980.036，终点里程为YDK10+261.695，区间长为1 281.659 m，隧道顶板埋深为10.00～18.50 m，盾构隧道直径为6.29 m。尚红区间工程地质剖面示意如图1所示。

盾构施工为左右线同时进行，盾构在掘进过程中主要位于中密卵石层〈2-9-3〉，砂卵石颗粒较为密实，且富含大漂石和地下水，盾构掘进较为困难。

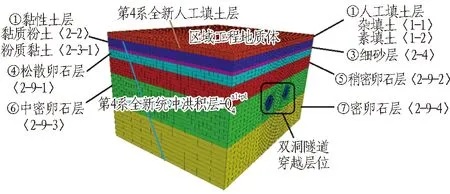
图1 尚红区间工程地质剖面示意图

对尚红区间盾构隧道拱顶以下2 m土体进行筛分试验，各粒径卵石含量比例如图2所示。总体来说，卵石粒径大部分在100 mm以上，颗粒粒径较大，盾构掘进存在较大困难。

图2 粒径分布饼状图

1.2 砂卵石地层特性

在大量工程资料及充分现场调研的基础上，分析得出尚红区间砂卵石地层主要有以下特性。

1)卵砾石多、粒径大，漂石含量高。卵砾石含量约占98%，最大粒径可达650 mm，卵石硬度高，最大抗压强度可达200 MPa以上。

2)地层内摩擦角大。盾构在该地层中掘进时经常会出现刀盘和螺旋输送机转矩大，并且在施工中经常会发生卡刀盘和卡螺旋输送机等问题。

3)地层磨蚀性强，对盾构耐磨性要求高。该地层具有较强的磨蚀性，盾构在该地层中掘进时对刀盘、刀具、螺旋输送机及盾体的磨损较严重，尤其是对刀盘、刀具及螺旋输送机的耐磨性要求高。

4)地层透气性、流动性强，整体稳定性差。在盾构掘进施工过程中，采用气体或液体添加剂进行开挖舱保压以确保地层稳定极为困难，且在盾构施工过程中经常会出现盾构排渣量超方、地表沉降值变化大等问题。

2 土体微观参数标定

2.1 参数标定方法

采用离散元软件EDEM进行刀盘掘进过程的仿真，需要对材料参数进行标定。需要设置的常用材料参数有密度、泊松比和剪切模量，材料接触参数有静摩擦因数、滚动摩擦因数和恢复系数。对于材料参数，可通过工程地质报告获取，而材料接触参数受环境影响较大，同一材料不同环境下的接触参数差距可能很大。因此，接触参数一般通过试验方法进行标定[8-9]。

土体参数标定试验方法有很多，如滑板试验、坍塌试验、三轴压缩试验以及堆积角试验。本次仿真过程涉及颗粒与颗粒之间以及颗粒与几何体之间的接触，采用堆积角试验进行土体微观参数的标定较为符合本文的仿真模型[10]。堆积角是物料在自身内力作用下自然下滑，达到稳定状态后，自由表面与水平面之间的夹角[11]。

2.2 参数标定仿真试验过程

为了使仿真结果更贴近于实际情况，颗粒形状模仿实际颗粒建立，如图3所示。颗粒物料密度根据地勘报告获取。由于颗粒含水率在软件中无法直接确定，而含水率与颗粒表面能量值有较强的联系，通过标定颗粒表面能量值，可以反映颗粒含水率的大小。

(a) 实际颗粒形状

(b) 仿真颗粒形状

仿真试验过程分为以下4部分：

1)建立长方体模型Box，该模型长为500 mm、宽为500 mm、高为700 mm，删除Box的顶面，并建立与实际砂卵石形状近似的颗粒模型，在Box上方建立颗粒工厂，并生成颗粒，如图4(a)所示；

2)当颗粒添加到一定量时，停止生成颗粒，并使其静态堆积一段时长，如图4(b)所示；

3)撤掉长方体某一侧面，使砂卵石颗粒在自身内力作用下沿长方体侧面自由下滑，如图4(c)所示；

4)当整个模型处于平衡状态时，测量土体堆积角，如图4(d)所示。

(a) 建立Box并生成颗粒 (b) 颗粒静态堆积

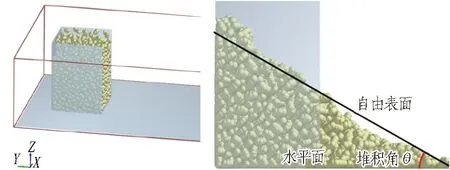
(c) 颗粒自由下滑 (d) 测量土体堆积角

2.3 参数标定仿真试验数据处理

本文堆积角仿真试验所使用的材料有2种，一种是物料颗粒材料，另一种是Box材料。颗粒材料参数采用砂卵石参数，Box材料参数采用盾构材料参数，这些参数可通过地勘报告以及刀盘设计说明书获取。砂卵石地层土体剪切模量为1.12×107Pa，密度为2 200 kg/m3，泊松比为0.27； 盾构材料剪切模量为7.9×1010Pa，密度为7 800 kg/m3，泊松比为0.25。

本次堆积角试验标定的参数包括颗粒表面能量值、静摩擦因数和滚动摩擦因数3个[12]。为了准确标定上述3个参数，根据实际情况设置4个能量值进行标定，分别为4、8、12、16 J，静摩擦因数和滚动摩擦因数同样设置4个值进行标定，静摩擦因数分别为0.2、0.4、0.6、0.8，滚动摩擦因数分别为0.01、0.02、0.03、0.04。对上述参数取值分别进行试验，一共要进行43=64组试验。为了减少试验次数以节约仿真时间，本文采用正交试验设计方法[11]进行试验设计，一共进行16组试验。仿真试验结果如表1所示。

2.4 参数标定结果

对于本次所需标定的卵石层〈2-9-3〉，取一定量的该地层砂卵石土体，按照正常掘进时的比例加入经过发泡后的泡沫及膨润土浆液进行渣土改良，充分搅拌后进行堆积角试验，如图5所示。经测量，其稳定堆积角为36°。试验中第7组和第8组所形成的堆积角与实际值较为接近，因此，参考第7组或第8组试验参数能更符合实际情况。

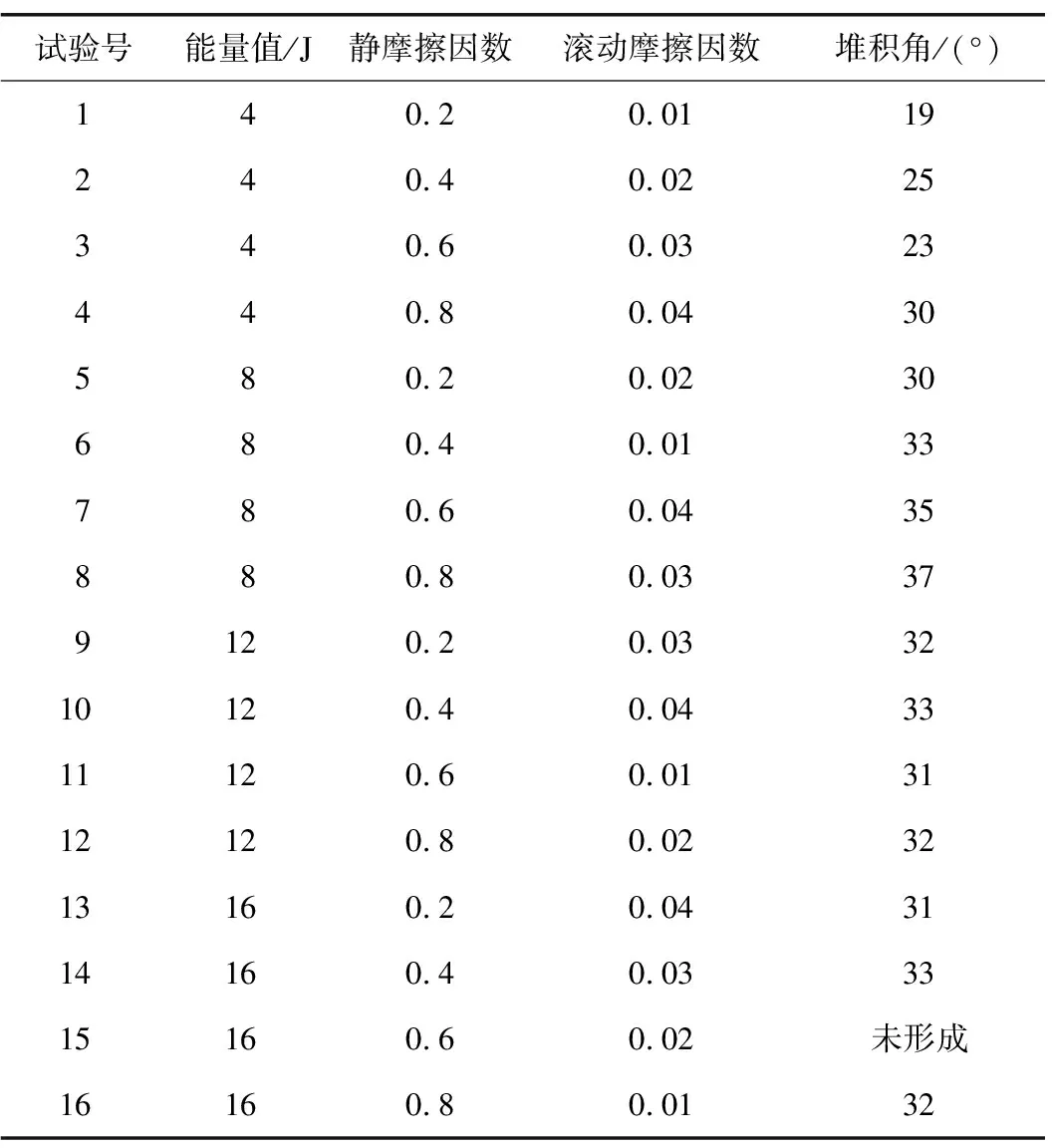
表1 仿真试验结果

图5 堆积角试验

结合本次堆积角仿真试验结果及文献[13-14]，最终确定本次离散元仿真模型接触参数如表2所示。

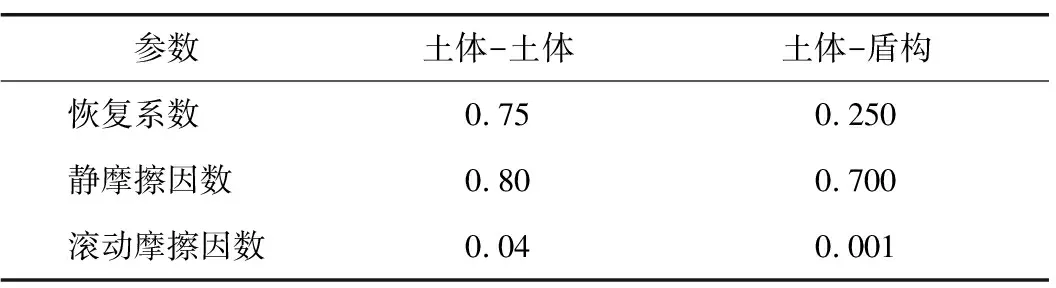
表2 仿真模型接触参数

采用上述确定的离散元仿真模型参数进行堆积角仿真试验，最后得到的土体堆积角为36.2°，与实际土体堆积角相近，故本次离散元仿真模型参数选取较为合理。

3 盾构掘进模型及相关参数控制

3.1 盾构掘进模型建立

盾构掘进系统主要由土体、刀盘、土舱、螺旋输送机组成。为了模拟盾构掘进过程，根据实际尺寸分别建立土体、刀盘、土舱及螺旋输送机三维模型，再组成盾构掘进系统模型，如图6所示。

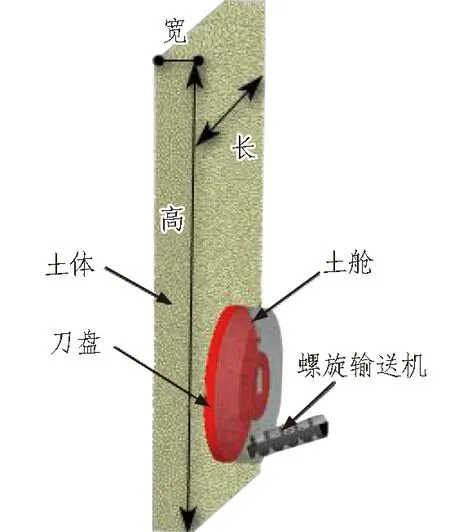
图6 盾构掘进系统模型

3.2 盾构掘进模型参数确定

3.2.1 土体模型参数

充分考虑到尚红区间实际工程地质情况和计算机运算能力，建立土体三维模型尺寸长为10 m，约为刀盘直径的2倍； 宽为1.6 m，为盘厚度的4倍； 高为20 m。刀盘顶端覆土厚度为11 m左右，与研究区间盾构埋深接近。

3.2.2 刀盘模型参数

刀盘参数取自研究区间其中1台盾构(DZ356)，其部分参数如表3所示。

表3 刀盘部分参数

3.2.3 土舱及螺旋输送机模型参数

土舱位于盾构前盾内部，土舱直径与刀盘直径相同，取为6 290 mm，土舱深度实际上略高于刀盘背面到法兰盘的距离。为了简化法兰连接处的复杂结构，将土舱深度取为刀盘背面到法兰盘背面之间的距离，其值为1 030 mm，土舱壳体厚度取为50 mm。

螺旋输送机安装角度为22°，固定在前盾底部套筒法兰上。由于该标段地层大粒径卵石含量高，卵砾石含量大，采用大直径螺旋输送机以便卵石顺利通过，其内径为920 mm，螺旋叶片截距为630 mm，螺旋轴转速为0～19 r/min。

3.3 仿真参数设置与步骤

3.3.1 全局参数设置

运用离散元软件EDEM进行仿真，首先需要定义全局仿真参数。全局仿真参数包括仿真名、接触模型、重力设置、材料参数以及接触参数。砂卵石接触模型选择运用Hertz-Mindlin(no slip)模型，由于本文不研究几何体磨损，因此颗粒与几何体的接触同样也运用Hertz-Mindlin(no slip)模型[15]。重力沿z轴设置为-9.81 m/s2，材料参数与接触参数按前述物料标定的参数进行取值。

3.3.2 几何体运动参数设置

在几何体仿真模型尺寸及位置确定后，需要对几何体运动进行定义。根据盾构掘进过程中各部件的运动情况，刀盘运动由2部分运动组成： 1)刀盘水平推进运动，2)刀盘旋转运动。土舱跟随盾构掘进一起做推进运动。螺旋输送机的运动同样由2部分组成： 1)水平推进运动，2)螺旋轴自身的旋转运动。各部件的运动情况如图7所示。速度根据实际工程进行取值，盾构掘进速度为66 mm/min，刀盘转速为1.6 r/min，螺旋输送机转速为9.5 r/min。

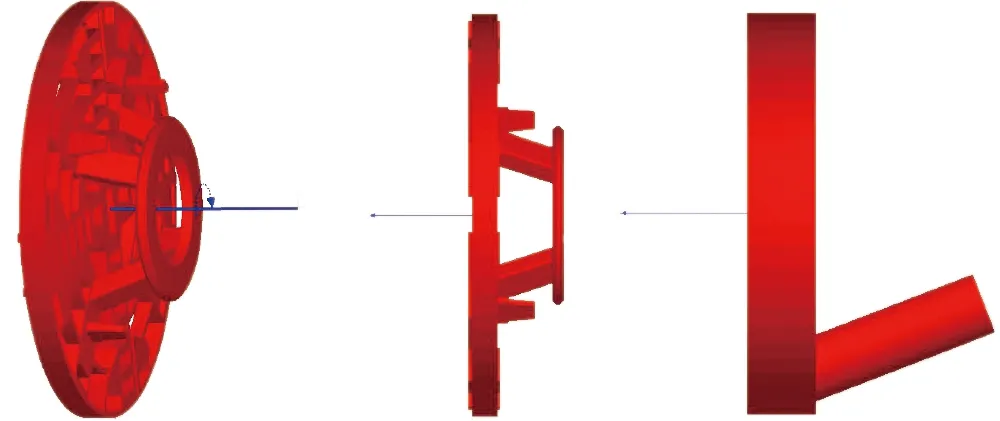
(a) 刀盘旋转运动 (b) 刀盘推进运动 (c) 土舱推进运动

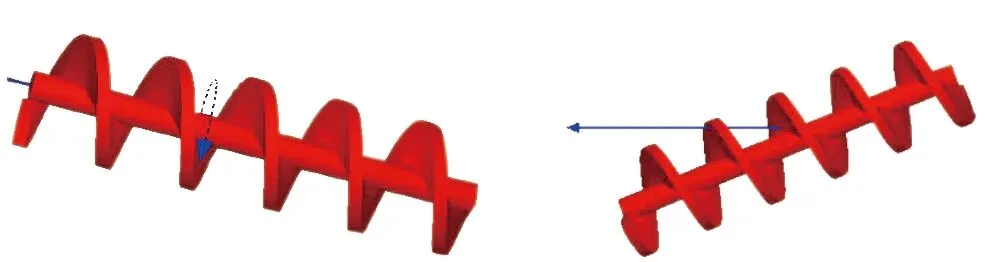
(d) 螺旋输送机旋转运动 (e) 螺旋输送机推进运动

3.3.3 仿真参数设置

仿真参数设置主要有仿真时间步长、仿真时间、数据保存间隔、网格大小以及计算机核心数。仿真时间步长通常取为瑞利时间步长的20%； 仿真时间为400～500 s；为防止数据量过于庞大，数据保存间隔设置为1 s； 网格大小为最小颗粒半径的3倍。

4 仿真结果分析

4.1 土体颗粒运动分析

图8示出刀盘掘进仿真过程中各阶段土体颗粒运动状态云图。图中不同的颜色表示不同的颗粒速度，红色表示速度较大，蓝色表示速度很小，绿色表示速度介于红色和蓝色之间。可以看出： 在刀盘掘进仿真初期，掌子面土体以较快速度涌入土舱； 随着仿真的进行，高速的土体颗粒在土舱底部发生沉积，颗粒运动速度在短时间迅速减小，低速的土体颗粒在螺旋输送机作用下以一定的速度排出土舱。由上述分析可知，土体颗粒在土舱底部发生较大幅度的速度变化，对螺旋输送机螺旋轴伸入土舱的部分产生较大冲击，因此在刀盘开挖初期应尽量控制刀盘转速，以降低对螺旋轴的冲击和损坏。

(a) 土体刚涌入土舱时 (b) 土体填充半舱时

(c) 土体即将填满土舱时 (d) 土体填满土舱时

4.1.1 刀盘前端土体的运动状态分析

图9示出刀盘前端掌子面土体颗粒在仿真前期和仿真后期的运动状态云图。由图9可知： 在盾构掘进仿真前期，掌子面土体颗粒整体上运动速度较快，颗粒运动范围也较大，且刀盘外围土体颗粒运动速度明显高于刀盘中心土体颗粒，掌子面上部的土体颗粒存在一定的运动速度； 在刀盘掘进仿真后期，刀盘掌子面土体颗粒整体上较前期运动速度有所减慢，颗粒运动范围随之有所减小，刀盘外围土体颗粒运动速度同样要高于刀盘中心土体颗粒，但掌子面上部的土体颗粒运动速度较前期显著减慢，土体流动趋于稳定。

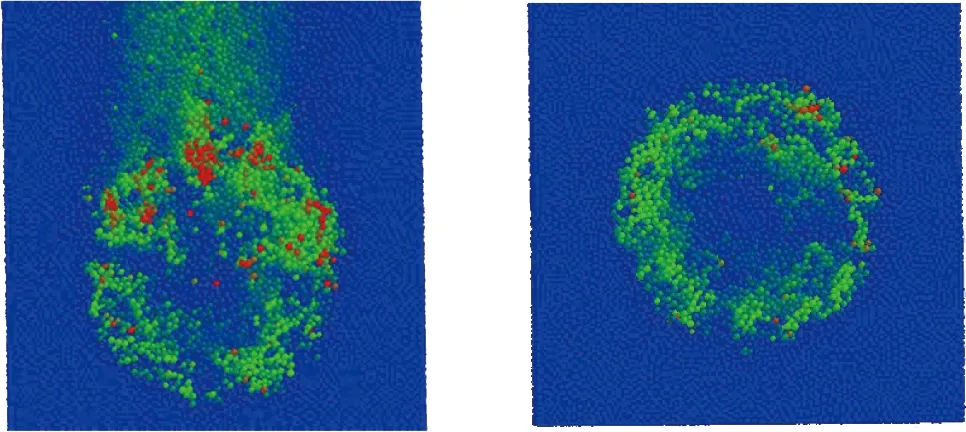
(a) 仿真前期 (b) 仿真后期

4.1.2 土舱内土体的运动状态分析

图10示出土舱正面、侧面以及剖面土体运动状态云图。由图10(a)可知： 土舱中心部位和螺旋输送机左右两侧土体颗粒运动速度较慢。由图10(b)可知： 土舱靠近刀盘侧土体颗粒运动速度要高于土舱背板侧土体颗粒。由图10(c)可知： 土舱外围土体颗粒运动速度明显大于土舱中心部位土体颗粒，且螺旋输送机螺旋轴伸入土舱部分的周围土体颗粒运动速度较大。

(a) 土舱正面 (b) 土舱侧面 (c) 土舱剖面

刀盘掘进过程中土舱内土体平均运动速度随时间变化曲线如图11所示。由图11可知： 在刀盘掘进仿真初期，土舱内土体平均运动速度较大，这是由于掌子面土体在水土压力及推进力作用下涌入土舱，获得较大速度，颗粒在重力作用下落入土舱底部； 当颗粒落入土舱底部后，在土舱底部进行堆积，运动速度迅速减小，并最终趋于平衡(图11中平均运动速度平衡值约为0.23 m/s)，平衡后的平均速度即可用于描述土舱内土体的流动性。

图11 土舱内土体平均运动速度随时间变化曲线

4.1.3 螺旋输送机内土体的运动状态分析

图12示出螺旋输送机内土体运动状态云图。螺旋输送机螺旋轴伸入土舱部分的周围土体颗粒运动速度明显大于螺旋输送机内部土体颗粒，土体颗粒运动速度减小会造成能量损失，其损失的能量由螺旋轴及螺旋叶片承担，这将导致螺旋轴和螺旋叶片的磨损，并减少其使用寿命。

图12 螺旋输送机内土体运动状态云图

4.2 土体颗粒受力分析

盾构掘进过程中土体颗粒的受力状态可以在一定程度上反映盾构掘进对土体颗粒的影响。反之，土体颗粒的受力状态可以影响刀盘、土舱以及螺旋输送机的各种性能。

4.2.1 刀盘前端土体颗粒受力状态

图13示出盾构掘进过程中刀盘前端土体颗粒所受压缩力云图，刀盘旋转方向为顺时针方向。可以看出： 刀盘右方和下方周围土体所受压缩力要高于刀盘上方周围土体，刀盘右下方受力较大，刀盘旋转过程中该部位受阻较大。因此，该部位是刀盘卡停问题中需要着重考虑的位置之一。可以对渣土改良喷口布置进行优化，着重对右下方土体注入泡沫或膨润土。

图13 刀盘前端土体颗粒所受压缩力云图(单位： N)

4.2.2 土舱内土体颗粒受力状态

图14示出刀盘掘进过程中土舱内土体颗粒所受压缩力云图，刀盘旋转方向为顺时针方向。由图14(a)可知： 土舱内土体颗粒所受压缩力大小总体上呈现左低右高的规律，土体颗粒所受压缩力最小值大致分布在土舱最上方处，最大值大致分布在土舱右下角处，此时螺旋输送机伸入土舱部分的螺旋轴受不均衡力的作用。由图14(b)可知： 土舱内土体颗粒所受压缩力大小还呈现出上低下高的规律，土体颗粒所受压缩力最大值大致分布在螺旋输送机上端，最小值大致分布在土舱最上方处。

(a) 土舱正面土体颗粒 (b) 土舱剖面土体颗粒

4.2.3 螺旋输送机内土体颗粒受力状态

图15示出刀盘掘进过程中螺旋输送机内土体颗粒所受压缩力云图。由图15可知： 螺旋输送机前端的土体颗粒所受压缩力较大，螺旋输送机中部土体颗粒所受压缩力较前端有所减小，在即将离开螺旋输送机时，土体颗粒几乎不受压缩力影响。螺旋输送机螺旋轴伸入土舱段通常是悬在土舱内部，缺少支撑，在土体压缩力作用下会产生较大应力，因此，土舱部位螺旋输送机易发生断轴风险。

图15 螺旋输送机内土体颗粒所受压缩力云图(单位： N)

4.3 刀盘和螺旋输送机有限元分析

对刀盘进行有限元分析，需要导出刀盘的受力数据。本文选取300～500 s的刀盘受力数据，数据格式为ANSYS可识别的axdt格式，运用EDEM与ANSYS耦合接口传输数据，进行刀盘有限元分析。在建立好耦合计算接口后，对刀盘施加约束和节点载荷，然后进行计算，得出刀盘应力与变形云图如图16所示。

(a) 应力云图(单位： MPa) (b) 变形云图(单位： mm)

由图16可知： 刀盘面板处应力较小，刀盘云腿、云腿与面板连接处及云腿与法兰盘连接处应力较大，最大应力值为123.27 MPa，位于云腿与法兰盘连接处； 变形量与刀盘半径有关，随着刀盘半径的增大，刀盘面板变形增大，刀盘变形量最大值位于刀盘最外围的环形梁，最大变形量为1.69 mm。

同样对螺旋输送机进行有限元分析，分析结果如图17所示，图中视角方向为螺旋输送机俯视方向，并进行视觉效果放大处理。

(a) 应力云图(单位： MPa)

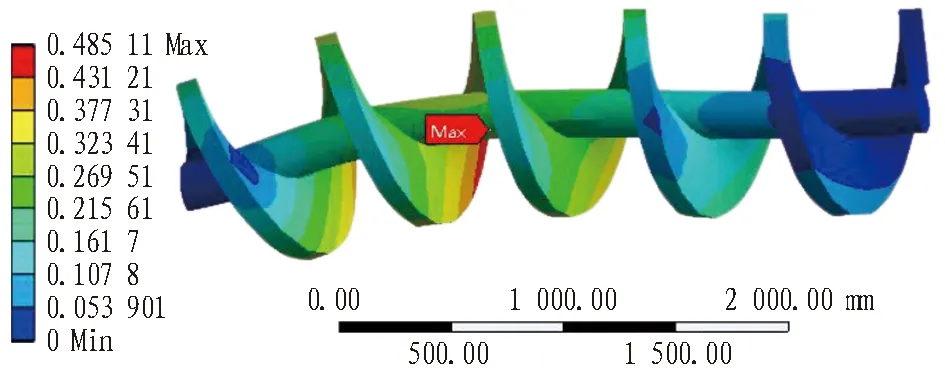
(b) 变形云图(单位： mm)

由图17可知： 螺旋轴靠近土舱段的应力和变形均大于其他部位，最大变形量为0.49 mm，位于土舱和螺旋输送机筒体连接处附近的螺旋叶片外圈，最大应力值为59.01 MPa，位于土舱后隔板和螺旋输送机筒体连接处； 螺旋轴在外力作用下向一侧弯曲，其弯曲方向为土舱左侧。由图14(a)可知： 土舱右侧颗粒所受压缩力大于左侧，螺旋输送机螺旋轴伸入土舱段受到不平衡外力，其螺旋轴易朝土舱左侧发生弯曲。由于螺旋输送机连续转动，外力将导致螺旋轴受到交变荷载而产生材料疲劳，这也是从理论上验证螺旋输送机螺旋轴存在较大的断轴风险的结论。

5 结论与讨论

本文通过建立离散元仿真模型分析盾构掘进过程中的土体运动和受力规律，并利用EDEM与ANSYS耦合对刀盘及螺旋轴进行有限元分析，得到以下主要结论。

1)在盾构稳定掘进过程中，刀盘掌子面外围土体颗粒运动速度要高于刀盘中心土体颗粒； 土舱内土体平均运动速度平衡值为0.23 m/s，可用于描述土舱内土体的流动性。土舱内存在2个土体颗粒运动速度较慢的部位： 一是土舱中心部位，说明此处易导致刀盘中心结泥饼； 二是螺旋轴伸入土舱段左右两侧土体，需考虑搅拌棒设置，以提高该部位渣土的流动性。此外，仿真结果表明螺旋轴伸入土舱部分周围土体颗粒运动速度明显大于螺旋输送机内部土体颗粒，说明土体的一部分能量消耗在与螺旋输送机的摩擦上。

2)刀盘掌子面土体及土舱内土体压缩力分布与刀盘旋转方向有关，当刀盘旋转方向为顺时针方向时，土舱内土体颗粒所受压缩力最大值分布在土舱右下方靠近螺旋轴处。

3)在刀盘掘进过程中，应力较大处基本集中于刀盘云腿，云腿与刀盘面板、法兰盘的连接处应力最大值为123.27 MPa，刀盘云腿与法兰盘连接处最大变形量为1.69 mm，位于刀盘最外围的环形梁；螺旋输送机螺旋轴最大应力值为59.01 MPa，位于土舱后隔板和螺旋输送机筒体连接处，最大变形量为0.49 mm，位于土舱和螺旋输送机筒体连接处附近的螺旋叶片外圈，在交变载荷作用下伸入土舱的螺旋轴存在较大的断轴风险。

本文得出的结论符合工程实际情况，使用离散元法模拟盾构掘进可为盾构研究提供新思路，但由于条件限制，仍有一些不足和有待探索之处。

1)本文的刀盘掘进模型较为简化，地层土体模型较小，土体颗粒较简单，且盾构模型除了刀盘、土舱及螺旋输送机外，并未建立盾构外壳模型，后续研究中可根据计算机能力不断进行完善。

2)针对刀盘及螺旋输送机的有限元分析是静态分析，而采用动态分析显然更为合理。因此，针对刀盘及螺旋输送机的动力学分析是值得研究的方向之一。