Gamma分布在海面目标检测中的应用*
周 围, 朱 勇, 杜玉晗, 谢俊好
(1. 中国电子科技集团公司第三十八研究所, 安徽合肥 230088;2. 哈尔滨工业大学电子与信息工程学院, 黑龙江哈尔滨 150001)
0 引言
雷达最重要的任务之一是目标检测。固定门限检测是一种经典的检测方法,它利用检测背景噪声、杂波水平的先验信息计算固定的检测门限,若回波信号的幅度超过门限则判定为目标。该方法在先验信息完全已知的均匀杂波背景下具有较好的效果,而在时变的杂波环境中检测性能会急剧下降。对海雷达在海面目标检测过程中不可避免地要接收到来自海面的后向散射信号,通常我们将这种信号称为海杂波。由于海杂波功率水平在实际情况中是时变的,通常难以设置一个合适的门限保证良好的检测概率和较低的虚警率,因此固定门限检测器几乎难以直接应用[1]。
为了在对目标正确检测的基础上保持恒定的虚警率,恒虚警(CFAR)处理技术在现代雷达检测系统中获得广泛应用[2-6],其核心思想是利用参考回波样本对未知检测背景的信息进行估计并自适应地设定检测门限,在特定杂波、噪声背景下实现目标的恒虚警率自动检测。为了选择、设计合适的检测器及工作参数,需要对杂波背景进行统计特性分析。研究海杂波幅度统计特性主要利用海杂波的回波包络或者功率进行非相干统计建模,对海面目标检测算法的设计具有重要意义。在低分辨率雷达中,海杂波可以用散斑(Speckle)模型来建模,其幅度概率密度函数服从瑞利(Rayleigh)分布。随着雷达距离分辨率的提高,海杂波幅度分布函数出现“拖尾”现象,并逐渐偏离瑞利分布。近年来,随着对海杂波形成机理及物理含义的进一步理解,复合高斯模型在高分辨海杂波统计建模上得到广泛认可与深入研究发展。学者们提出了多种复合分布模型,如K分布[7]、K+N分布[8]和帕累托分布[9]等,并利用大量的实测数据进行验证。
需要注意的是,在实际情况中,检测器类型和参考窗长度需要根据杂波背景和实际干扰目标特性来决定,虽然近年来CFAR检测得到广泛研究,但最优、通用的CFAR检测器是几乎无法获得的[10],因此在设计检测方法、制定检测准则时必须仔细考虑实际检测背景。同时,虽然经过长期的研究分析,学者们对于海杂波的物理机理已有相对成熟的结论,但由于其散射机制的复杂性以及杂波特性对实际雷达系统参数、外界环境的依赖性,在实际应用中很难找到一个与海杂波实际情况完全符合的模型[11],目前人们对海杂波特性的研究与建模仍然主要依靠实际测量值与观察结果。
为丰富海杂波建模方式、进一步提升海杂波中目标恒虚警探测能力,本文结合大量实测数据处理结果,详细分析了利用Gamma分布对海杂波幅度统计特性建模拟合的可行性,同时介绍了两种基于Gamma分布海杂波背景下的CFAR检测器,通过理论分析和计算机仿真验证了它们在均匀杂波背景和非均匀杂波背景下的检测性能。结果表明,海杂波的幅度分布可以用Gamma分布进行建模,且提出的两类CFAR检测器在各类典型杂波背景下具有良好的目标检测能力和鲁棒的虚警控制能力。
1 Gamma分布与拟合结果
1.1 Gamma分布
Gamma分布的概率密度函数如下所示:
(1)
式中,x为雷达回波幅度,α和β分别为形状参数和尺度参数,Γ(·)为Gamma函数。相应地,Gamma分布的累计概率密度函数(CDF)可以表示为
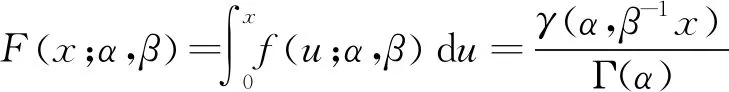
(2)
其中γ(s,x)为低阶不完全Gamma函数,定义为

(3)
Gamma分布随机变量的n阶矩可以表示为
(4)
作为一种双参数概率密度函数,Gamma分布族的形状可以通过改变其中一个参数(例如形状参数α)来进行灵活调整,如图1所示。这意味着Gamma分布可以用于描述不同海面环境下的杂波统计特性。由图1可以看出,当形状参数较小时Gamma分布概率密度函数出现明显拖尾,反之则概率密度函数趋于“平坦”。

图1 不同形状参数下的Gamma分布概率密度函数
1.2 实测海杂波数据统计分析
本节中,共统计分析来自3个实测海杂波数据库的样本,它们分别来自3次大型外场试验。其中,2个数据库来源于某X波段对海ISAR试验雷达(以下简称“试验雷达”),分别采集于中国山东省青岛市和威海市,另外一个数据库来源于加拿大McMaster大学研制的IPIX相参全极化雷达(以下简称“IPIX雷达”)。
1.2.1 试验雷达实测数据统计结果
本节对实测海杂波的幅度进行概率密度函数模型的拟合优度检验(Good-of-Fitness Test),待测试概率密度函数(PDF)包括瑞利分布、Gamma分布、对数正态分布、K分布、K+N分布、韦布尔分布和帕累托分布。在本例中,瑞利分布、Gamma分布、K分布、K+N分布和帕累托分布的分布参数由矩估计方法获得,对数正态和韦布尔分布的参数可通过最大似然估计方法(MLE)来获得[12]。
图2(a)给出了试验雷达在青岛采集的实测数据的直方图拟合结果。图中横坐标为归一化幅度,纵坐标为互补累计分布函数(1-CDF)。考虑到K+N分布是K分布的广义形式,因此在图2(a)中省略了K分布的拟合结果。从图2(a)中可以直观看出,实测海杂波的幅度统计分布可以近似由Gamma分布来拟合。
为了获得更为精确、定量的拟合结果,通常采用χ2检验来进行拟合优度检验。χ2检验统计量可以表示为
(5)
式中,Nbin为分组数,Ai为观测频数,Ti为理论频数。
表1给出了试验雷达在青岛采集的海杂波数据的参数估计与χ2检验统计结果。在这批数据来自6个距离单元,每个距离单元包含3 000个海杂波时域回波样本。从表1的统计结果可以看出,Gamma分布的χ2检验统计结果最小,即Gamma分布在这三者中具有最优的拟合性能。

表1 海杂波参数估计与拟合优度检验结果(青岛数据)

续表
图2(b)给出了试验雷达于山东威海采集的海杂波数据统计结果。这批数据一共包含了来自30个距离单元的海杂波时域回波,每个距离单元共包含16 384个样本。从图中可以看出,Gamma分布可以很好地对海杂波幅度进行建模。

(a) 青岛实测数据拟合结果
考虑到已有研究证明K+N分布和帕累托分布对实际海杂波的拟合效果优于对数正态分布和韦布尔分布[9,13],图3给出了利用Gamma分布、 K+N分布和帕累托分布对在威海采集的海杂波数据的拟合优度结果。图3的结果表明,Gamma分布具有相对更小的χ2值,即更优的拟合效果。

图3 Gamma,K+N和帕累托分布拟合优度检验结果(威海数据)
1.2.2IPIX雷达实测数据统计结果
本节统计分析IPIX雷达于1993年在Dartmouth采集的实测数据,其雷达参数与数据相关信息见表2。

表2 IPIX雷达参数
为了尽量避免不同的外界环境对统计结果带来的影响,提高分析结果的代表性,本例中主要研究数据文件#310和#311。这两批数据文件的采集时间和对应的海况天气与试验雷达的数据类似。每个数据文件包含14个距离单元,每个距离单元包含217个时域样本。其中,由于第6至第9个距离单元中含有合作目标的回波信息,因此在杂波统计时将这几个距离单元的数据剔除。
图4给出了IPIX雷达实测数据的直方图拟合结果,其中横坐标为归一化幅度,纵坐标为互补累计分布函数。从图中可以看出,Gamma分布、K+N分布和帕累托分布皆可以描述真实海杂波的幅度统计模型。表3和表4给出了利用上述3种分布对这两批数据建模的统计分析与拟合优度检验结果。结果表明,Gamma分布相比于K+N分布具有相对更小的χ2值;经计算,帕累托分布的χ2值远大于Gamma分布与K+N分布,因此在表中将其省略。因此,利用Gamma分布对实际海杂波幅度分布进行统计建模是合理的,这也为后续的目标检测奠定了基础。
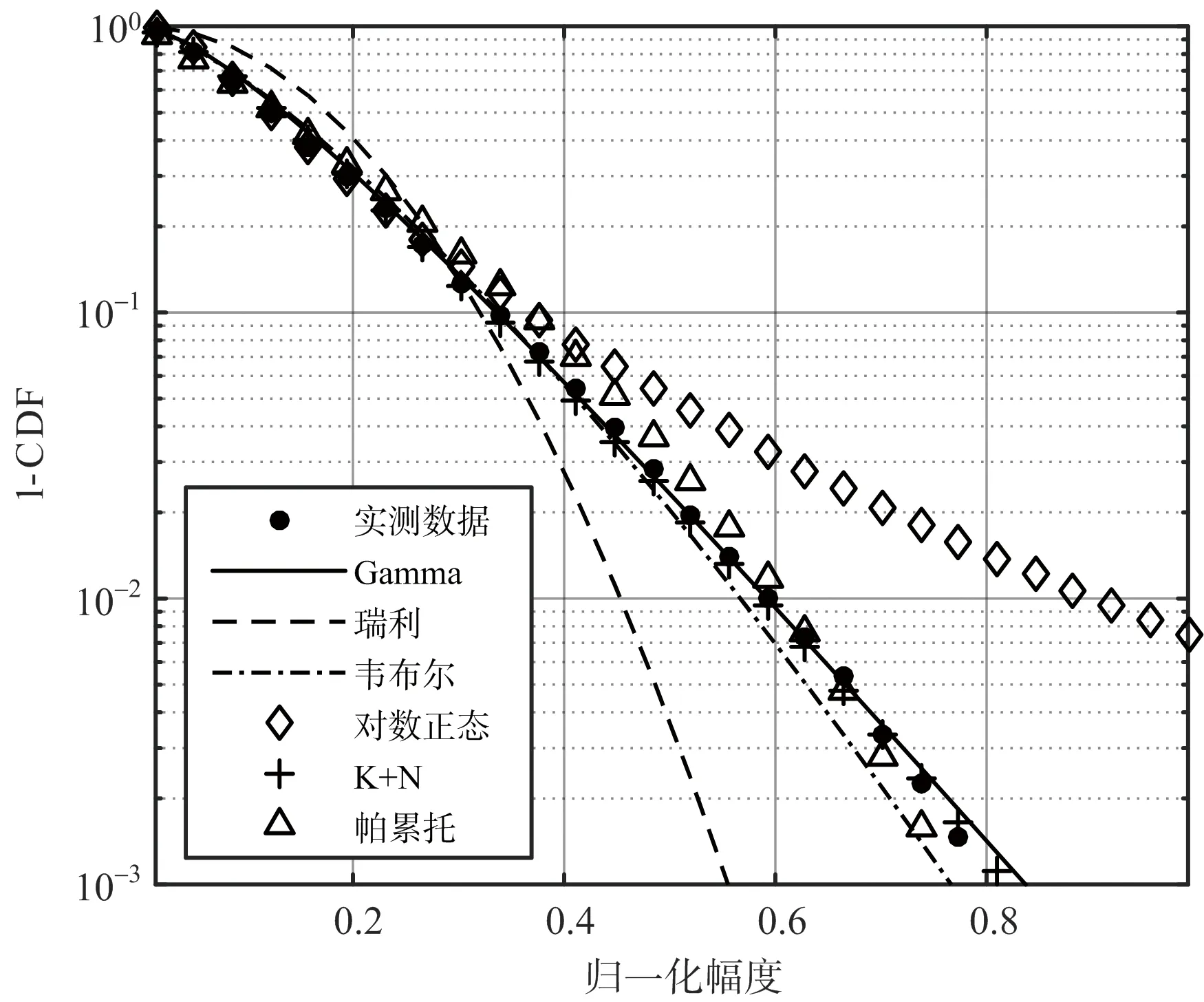
图4 IPIX雷达实测数据拟合结果

表3 海杂2检验结果(IPIX #310数据)

表4 海杂波χ2检验结果(IPIX #311数据)
2 Gamma分布海杂波下的目标检测
2.1 固定门限检测
当检测背景样本服从如式(1)所示的Gamma分布时,则固定门限检测器的虚警率可以表示为

式中,T为检测门限。
将e-t进行幂级数展开,式(6)可以改写为

(7)
几种典型形状参数下的虚警率结果如图5所示。从图中可以看出,当门限值给定时,其虚警率对形状参数仍有依赖性。这意味在实际工作中,杂波背景的形状参数需要作为先验信息提供给检测器。事实上,几乎在所有雷达系统工作之前,都需要事先对监视海域进行观测,获得并分析大量的杂波数据来对雷达系统各项信号处理技术方法进行评估。在雷达系统实际工作时可以事先收集足够的真实海杂波数据,利用Gamma分布对海杂波进行建模分析并将估计出的形状参数作为先验信息;这种处理方式也类似于杂波图法[14]。此外,当监视区域距离范围跨度较大时,可以将监视区域按照距离或者估计出的形状参数分割为若干个子区域[15],在进行目标检测时可以根据各个子区域的特点给检测器配置不同的参数。为不失一般性,本文后续分析皆假设形状参数先验已知。

图5 固定门限检测器在不同形状参数下的虚警率
固定门限检测器在不同形状参数下的检测概率如图6所示。由图6易知,这类检测器在不同形状参数下的检测性能差异较大。同时,由于实际环境下海杂波的时变特性,这类检测器几乎仅存在理论上的可用性,无法适应现代雷达系统的应用。

图6 固定门限检测器在不同形状参数下的检测概率
2.2 基于最大似然估计的CFAR检测器
2.2.1 检测器设计
CFAR检测器通常采用滑窗技术,其基本流程框图如图7所示。经过检波后的雷达回波样本序贯存储在延迟线上,根据具体用途将其分为CUT、参考单元和保护单元。CUT为感兴趣的待检测单元;参考单元中的回波样本用来估计杂波的平均水平;为了避免CUT中目标的能量泄漏到参考窗内而影响杂波水平估计,在CUT的两侧通常放置若干个保护单元。自适应检测门限可以表示为杂波水平估计值与乘积因子的乘积,当CUT中样本的强度超过该门限,则判定目标存在。

图7 CFAR检测器基本流程图
考虑到实测雷达海杂波幅度分布可以用Gamma分布进行建模拟合,本节介绍一种基于最大似然估计的Gamma分布海杂波背景下的CFAR检测器,即MLG-CFAR[5]。
MLG-CFAR检测器利用MLE方法对杂波平均功率进行估计。假设参考窗中的样本是独立同分布的Gamma随机变量X1,…,XNr,其中Nr为参考窗的长度,则参考单元样本幅度的似然函数可以写为
L(α,β|X1,…,XNr)=
(8)
考虑似然函数L恒为正,因此可以在上式的两端同时取自然对数,从而得到
lnL(α,β|X1,…,XNr)=
-Nrαlnβ-NrlnΓ(α)+

(9)
尺度参数β的最大似然估计可以通过解如下所示的一元方程获得:
(10)
由式(10)可以得到尺度参数的估计值为
(11)
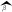
mp=Γ(α+p)βp/Γ(α)
(12)
则杂波平均功率的MLE(即MLG估计器)可以表示为
(13)
式中,E[·]为求数学期望,α为已知的形状参数。易证MLG估计器是对Gamma分布杂波平均功率的一种渐进有效的估计器。
2.2.2 在Gamma背景下的检测性能

(14)
通过随机变量的参数变换,可获得z的概率密度函数为
(15)

MLG-CFAR检测器对杂波背景的平均功率估计值及其概率密度函数已由式(12)和式(15)给出,则该检测器在Gamma分布下虚警率表达式为

(16)
式中,TMLG为归一化乘积因子。式(16)中不包含β,且由于形状参数α为已知的先验信息,所以MLG-CFAR的虚警率仅与归一化乘积因子TMLG有关,这表明MLG-CFAR检测器对尺度参数β是恒虚警的。
图8(a)和(b)分别给出了上述检测器在均匀杂波背景下、不同信杂比时的检测概率曲线和信杂比为15 dB时的接收机工作曲线(ROC)。本例中,设检测背景为各向同性的Gamma分布杂波,α=2,β=100。上述各类检测器的参考窗总长度都为16,左、右两个保护窗长度都为3,给定期望虚警率为Pfa=10-6。为了提高仿真结果的精度,本例中针对每一组参数都进行了105次独立蒙特卡洛实验。由图8中的结果可以看出,MLG-CFAR相比于上述各类CFAR检测器都具有最优的检测性能。

(a) 检测概率
图9给出了几类检测器在非均匀背景下的检测性能。非均匀杂波背景下主要包含了杂波边缘和多目标两种情况。在杂波边缘主要关注CFAR检测器的虚警率控制能力,在多目标情况下主要关注CFAR检测器对主目标的检测能力。图9(a)给出了上述几种CFAR检测器在杂波边缘的虚警率变化曲线。其中,检测场景共包含48个距离单元,其中第25个距离单元为杂波与瑞利噪声区域的交界位置。本例中,杂波幅度服从形状参数α=2、尺度参数β=100的Gamma分布,且杂噪比为10 dB。各类CFAR检测器的参考窗总长度都为16,左、右两个保护窗长度都为3,期望虚警率设为10-3。由仿真结果可以看出,在杂波边缘GO-CFAR具有最优的虚警率控制能力;虽然MLG-CFAR的虚警率控制能力并不让人很满意,但是其性能与CA-CFAR和OS-CFAR相当。
为了更有针对性地对检测性能进行分析与对比,本文结合实际雷达回波,主要考虑了3种多目标情形的假设:1)参考窗内有一个干扰目标,其干杂比(ICR)为10 dB;2)参考窗内有一个干扰目标,该目标具有与CUT内主目标相同的功率;3)参考窗内有5个干杂比为10 dB的干扰目标。为了更好地验证多目标情况下的“遮盖效应”,避免引入由于目标RCS起伏带来的额外干扰项,这几类目标的幅度都设为非起伏模型。
图9(b)至(d)分别给出了各类CFAR检测器在上述3种多目标情况下的检测性能。在图9 (b)中,参考窗内存在一个干扰目标,其干杂比为10 dB。由图中检测概率曲线可以明显观察到,由于“遮盖效应”的存在,CA-CFAR和GO-CFAR的检测性能有所下降。OS-CFAR在估计杂波平均功率时进行了排序处理,因此该检测器在多目标的情况具有较大优势。本例中,OS-CFAR检测器中的样本次序指数设为12,即在参考窗总长度为16时最多可容忍4个干扰目标。考虑到本仿真中仅有一个干扰目标,因此OS-CFAR具有较好的鲁棒性。随着主目标信杂比的逐渐增大,CA-CFAR和OS-CFAR的检测性能逐渐趋近。相比于其他几种CFAR算法,当主目标信杂比比较高时,MLG-CFAR具有较大的优势;当主目标信杂比相对较低时,MLG-CFAR的检测性能明显优于CA-CFAR和GO-CFAR,仅略逊于OS-CFAR。
图9(c)给出了干扰目标的功率与主目标的功率相等时的检测概率曲线。此时,OS-CFAR具有良好的检测性能,而CA-CFAR和GO-CFAR由于严重的“遮盖效应”,在进行目标检测时出现饱和状态,即无法正确检测主目标;这种情况可以通过适当增大参考窗长度来缓解。虽然此时MLG-CFAR的检测性能不尽如人意,但依旧具有一定的鲁棒性,不会出现检测饱和的极端情况。
图9(d)考虑了参考窗内同时出现5个不起伏的干扰目标的情况,每一个干扰目标的干杂比都是10 dB。考虑到此时干扰目标数目为5个,已经超过了OS-CFAR的容忍范围,因此OS-CFAR的检测性能急剧下降。由于GO-CFAR的选大特性,依然会受到“遮盖效应”的影响而难以达到理想的检测性能,但由于其杂波平均功率是Nr/2个样本的算术平均值,干扰目标带来的影响得到一定的削弱,所以检测性能相对于OS-CFAR有一定改善。CA-CFAR通过对Nr个杂波样本的功率求算数平均来获得杂波平均功率的估计值,样本数目比GO-CFAR多一倍,因此能够进一步削弱由干扰目标带来的影响,获得相对于GO-CFAR较优的检测性能也是符合预期的。MLG-CFAR检测器在上述几种CFAR检测器中获得最优的检测性能。

(a) 杂波边缘的虚警率(α=2,β=100)
2.3 加权幅度循环迭代CFAR检测器
2.3.1 检测器设计
在非均匀杂波背景下影响CFAR检测能力的主要原因是此时参考样本不再满足独立同分布的假设,导致检测器对杂波平均功率的估计出现偏差,进而造成虚警率的上升和检测概率的下降。如果一个检测器在估计杂波平均功率时能够最大程度地削弱异常值、尖峰或者潜在干扰目标的影响,那么可以预测该检测器在非均匀杂波背景下能具有良好的鲁棒性与适应性。基于上述思路,本节介绍了一种基于加权幅度循环迭代的CFAR检测器(WAI-CFAR)[2]。
WAI-CFAR检测器对杂波平均水平的估计是一个循环迭代过程,它主要包括两个步骤:排序和加权平均。假设参考窗中的样本是独立同分布的Gamma随机变量数据集:
(17)
则这些样本经过升序排列后为
{X(1),X(2), …,X(Nr)}
(18)

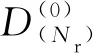
X(1)=ηwX(1)+(1-ηw)X(Nr)
(19)
式中,ηw为加权因子且ηw∈[0,1]。将由式(19)获得的处理结果放回剔除幅度最大和最小的样本后的数据集,可获得经过一次循环迭代处理之后的新数据集,即
(20)
对式(20)给出的新数据集继续进行升序排列,可以获得升序之后新样本序列,即
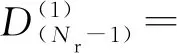
{X′(1),X′(2), …,X′(Nr-1)}
(21)

(22)
WAI-CFAR检测器中的加权系数ηw可以根据实际需要灵活选取。当ηw=0.5时,一次WAI处理输出的结果为两个输入样本的幅度算术平均;当ηw>0.5时,幅度较小的样本在最终输出结果中贡献较大;反之,则幅度较大的样本具有更大的贡献。本文主要分析了WAI-CFAR检测器在5种典型的加权系数下的性能,如表5所示。

表5 5种典型的加权系数
2.3.2 在Gamma背景下的检测性能
图10给出了WAI-CFAR检测器在不同Gamma分布参数和不同加权系数下的虚警概率曲线。为不失一般性,本例中检测器的参考窗总长度为16,左、右两个保护窗长度都为3。为了更好地体现WAI-CFAR在不同尺度参数下的通用性,仿真分析中主要考虑了β=100,150,1 000,1 500和10 000五种情况。为了保证蒙特卡洛仿真的精度,针对每一种参数组合都进行了109次独立的蒙特卡洛试验。
图10(a)给出了当α=0.5时WAI-CFAR检测器在不同尺度参数时的虚警率曲线,其中5种典型加权系数由表4给出。由图10(a)可以看出,当加权系数给定时,WAI-CFAR检测器在不同尺度参数的Gamma分布杂波中的虚警率曲线几乎是各自重叠在一起,这说明此时的虚警率仅随乘积因子的变化而变化,与尺度参数β的取值无关。考虑到蒙特卡洛仿真的精度有限,经过局部放大虽然可以观察到不同尺度参数下的虚警率曲线并不完全相同,但其微小差异可以忽略不计。
图10(b)和(c)分别给出了当α为2和10时的虚警率曲线。仿真结果证明,尽管WAI-CFAR检测器在Gamma分布杂波中的虚警率对形状参数α有依赖性,但该检测器在形状参数给定时对尺度参数具有恒虚警特性。

(a) 形状参数为0.5
图11(a)和(b)分别给出了上述几种检测器在期望虚警率为Pfa=10-6时的检测概率以及当目标信杂比为16 dB时的接收机工作曲线。本例通过蒙特卡洛方法获得上述定量结果,同时为了提高仿真结果的精度,对于每种参数下的检测概率估计都进行了105次独立试验。由结果中可以看出,CA-CFAR检测器和加权系数为参数2和参数3的WAI-CFAR检测器的检测性能相当,且优于OS-CFAR和GO-CFAR检测器。
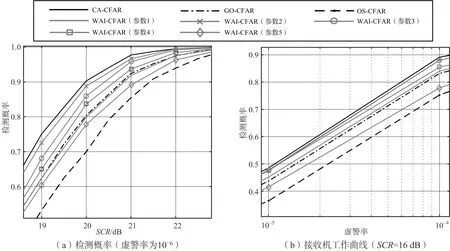
图11 CA,GO,OS和WAI-CRAR在均匀Gamma背景下的性能(α=2,β=100)
图12(a)给出了上述几种CFAR检测器在杂波边缘的虚警率变化曲线。为保证仿真结果对比的客观性,本例中检测场景仿真参数与图9一致。由仿真结果可以看出,CA-CFAR的虚警率在杂波边缘急剧上升,OS-CFAR的虚警率控制能力也不尽如人意,而GO-CFAR具有最优的虚警率控制能力。此时,WAI-CFAR检测器的虚警率变化情况与加权系数的选择有关。在加权系数为参数3,4和5时,WAI-CFAR的虚警率控制能力较差;当加权系数为参数2时,WAI-CFAR的虚警率在杂波边缘有一定上升且高于GO-CFAR,但是明显低于CA-CFAR和OS-CFAR检测器;WAI-CFAR在加权系数为参数1时的虚警率控制能力整体上优于其他几种方法。
在图12(b)中,参考窗内存在一个干杂比为10 dB干扰目标。由结果中可以看出,由于“遮盖效应”GO-CFAR的检测性能急剧下降。由于WAI-CFAR检测器可以利用加权系数进行灵活配置,当加权系数为参数2到参数5时性能较优,当目标信杂比较高时甚至优于OS-CFAR检测器。
在图12(c)中,参考单元中包含一个与主目标的功率相等的干扰目标。此时,OS-CFAR在估计杂波平均水平时通过样本幅度排序将干扰目标的信息剔除,在干杂比较大的情况下也具有良好的检测性能。由于严重的“遮盖效应”,CA-CFAR检测器的检测性能急剧下降。GO-CFAR和加权系数为参数1的WAI-CFAR检测出现饱和状态,无法正确检测主目标。WAI-CFAR在加权系数为参数4或参数5时具有较为鲁棒的性能,其定量结果与OS-CFAR检测器相当。
图12(d)考虑了参考窗内同时出现5个干杂比为10 dB的干扰目标的情况。此时,由于干扰目标数目超过了OS-CFAR检测器的抗干扰能力的极限,OS-CFAR的检测性能急剧下降,只有当主目标的信杂比充分大(例如31 dB)时,才能获得大于90%的检测概率;严重的“遮盖效应”同样导致CA-CFAR和GO-CFAR的检测性能难以令人满意。当加权系数为参数4或参数5时,参考窗中幅度较小的样本对杂波平均水平的估计值贡献较大,此时即使干扰目标的干杂比较大,但经过加权平均后对最终的输出统计量不会产生严重影响,因此此时WAI-CFAR检测器具有最优的检测性能。

图12 CA,GO,OS和WAI-CFAR在非均匀Gamma背景下的检测性能
3 结束语
本文首先利用在中国青岛、威海采集的X波段海杂波实测数据以及加拿大McMaster大学提供的X波段雷达海杂波实测数据进行统计分析,证明了海杂波幅度分布可以Gamma分布来进行建模,并给出了直观的直方图拟合结果和定量的拟合优度检验结果。随后介绍了两种适用于Gamma分布杂波中的CFAR检测器,即MLG-CFAR和WAI-CFAR。理论分析和仿真结果表明,这两类检测器在Gamma分布形状参数已知的前提下对尺度参数具有恒虚警特性,且在均匀杂波背景和非均匀杂波背景下相比于几类经典CFAR算法具有更优的检测性能。

