量测噪声环境下反应堆功率模型预测控制研究

方愿捷，吕厚义，王骏杰，袁啸林，张 炯，江佳琦，刘婷婷，陈孟元

(1.巢湖学院 电子工程学院，安徽 合肥 238000；2.国网安徽电力有限公司临泉供电公司，安徽 阜阳 236400；3.中国科学院等离子体物理研究所，安徽 合肥 230031；4.安徽工程大学 电气工程学院，安徽 芜湖 241000)

火电机组已经广泛地参与到电网的调峰控制中，随着核电机组的控制技术日趋成熟，核电机组的负荷跟踪控制将是未来重要的调峰方式。核电机组负荷跟踪控制的关键是反应堆功率控制，基于经典的PID及其优化改进方法得到了大量关注。文献[3]采用了优化模糊PID的控制器实现了对反应堆功率的控制；文献[4]研究了模糊PID控制器及PID控制器在反应堆功率控制中的切换问题；文献[5]研究了反应堆堆芯功率在不同阶段下模糊系统与PID控制器的切换方法；文献[6]探讨了采用分数阶PID对反应堆的功率进行控制的可行性等。毫无疑问，PID控制是经典控制理论中的最典型应用，但是在控制性能越来越高的要求下，传统PID控制环节中缺少了对提升控制性能的考量。模型预测控制(MPC)首先在工业界得到应用，在学术界得到稳定性证明后，该方法被广泛应用到非线性系统中。模型预测通过在控制器中内置预测模型与目标优化函数参与到系统的反馈控制中，可以划分为动态矩阵方法(DMC)、模型算法控制(MAC)以及广义预测控制(GPC)。近年来多有研究者将模型预测控制应用到反应堆的功率控制中。文献[8]针对反应堆堆芯功率系统构建预测控制函数，并利用二次规划求解方法实现了目标函数的求解；文献[9]对反应堆的模型预测控制的控制量为棒速的增量控制；文献[10]考虑了模型不确定性情形下反应堆功率的预测控制。大量研究表明，预测控制对反应堆堆芯功率这一非线性模型的控制有着卓越的控制效果。但是，在反应堆预测控制的反馈校正环节，未考虑到反馈的量测环节的噪声影响。

量测噪声广泛存在于控制环节中，其中在辨识环节、控制环节、传感器检测环节均有大量学者对其进行研究。反应堆中子检测器是检测反应堆堆芯中子密度的重要设备，各文献均对其稳定工作等开展了研究。但在核电的闭环设计中，需要对反馈环节的量测噪声进行综合考虑设计。

相关的反应堆功率控制还有许多相关的研究正在得到关注，例如反应堆的backstepping控制、内模控制等，研究将对反应堆堆芯量测噪声下的模型预测控制实现及其性能进行分析。

1 包含量测噪声的反应堆功率模型

核电站反应堆通过链式反应不断产生中子，中子是激发下一次链式反应的关键。反应堆中的中子密度从某种程度上表征了反应堆的功率。为了实现可控的裂变过程，在反应堆中装备了可以吸收中子的控制棒，通过控制棒在反应堆的移动中实现中子密度的控制，进而控制反应堆的功率。反应堆的功率受到冷却剂的温度影响，冷却剂不断将堆芯功率带出，在蒸发器中实现热交换，因此反应堆模型还包含热工水力学模型。同时因为控制棒的运动带来反应性的变化，所以整个反应堆功率模型包含中子动力学模型、热工水力学模型与反应性模型。

反应堆堆芯实际模型中涉及上述多种机理模型，整体呈现出非线性耦合的复杂特征。使用单组缓发中子等效可以替代多组缓发中子，使得模型简化。进一步利用非线性模型在平衡点处线性化可以将反应堆堆芯功率系统等效成线性参数变化模型(LPV模型)。等效LPV模型可以改写为：

(1)

式中，状态向量

χ

(

t

)=[

δn

,

δC

,

δT

,

δT

,

δρ

]，算子

δ

表示在平衡点的偏移量，例如，

δn

=

n

-

n

；状态变量中

n

表示反应堆中子密度;

C

表示等效单组缓发中子份额;

T

表示燃料温度;

T

表示冷却剂出口温度;

ρ

表示控制棒移动带来的反应性；

u

(

t

)表示控制棒的棒速；

w

(

t

)表示量测噪声为符合均方为0的白噪声；

η

(

t

)表示输出量，即反应堆中子密度。

同时，式(1)中矩阵满足：

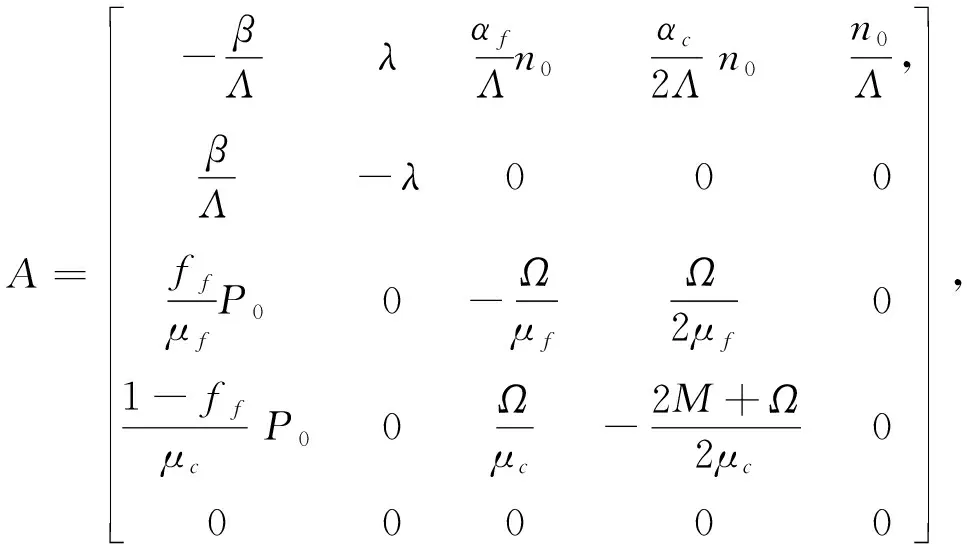
E

=[1]。中子密度是触发反应堆链式反应的关键。反应堆的功率

P

与中子密度

n

近似成线性关系，即

P

=

nP

，反应堆的控制实际可以等同于中子密度的控制。系统矩阵中的参数如表1所示。

表1 反应堆状态空间物理参数[9]

反应堆的实际状态空间中不可避免存在着大量量测噪声，中子探测器在量测过程中反馈中子密度会被传感器的噪声所污染，而非线性系统中对扰动的影响较为敏感，故研究对状态空间建模了均方为0的白噪声

w

(

t

)。噪声

w

(

t

)将直接影响到被量测的功率值，进一步给构建闭环的反应堆控制系统带来困难。

2 模型预测控制策略

模型预测控制基本原理为：在MPC控制器中内置一个接近真实系统的预测模型(预测模型)，遵循与参考轨迹偏差最小与控制信号能量最优的目标函数求解计算获得控制序列(滚动优化)，计算出来的控制信号被作用于真实系统中，被控对象在输入量的作用下产生新的输出量反馈于控制系统实现反馈作用(反馈校正)。

2.1 预测模型综合

结合模型预测控制方法，相应的反应堆模型预测控制系统框架如图1所示。根据式(1)构建预测模型，预测模型的状态空间需先进行离散化。因为噪声在建模中无法预测，因此在MPC控制器内的预测模型不包含噪声，这使得模型与实际无法做到完全匹配，影响控制效果，控制器的预测模型如式(2)所示。

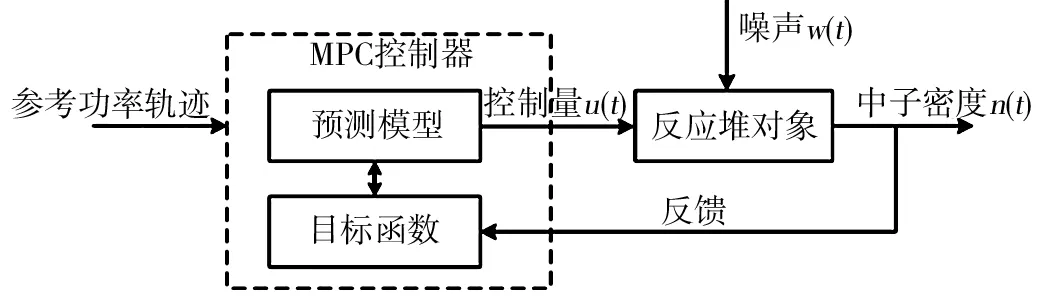
图1 反应堆功率模型预测控制系统框图

(2)

根据模型预测理论，通过求解问题，施加特定的控制序列

U

(

k

)=[

u

(

k

),

u

(

k

+1),…,

u

(

k

+

Nc

)]会在预测模型(2)中计算出预测的

N

步后的轨迹，可以得到：

(3)

将模型的递推结果改写成矩阵形式：

Y

(

k

)=

Fχ

(

k

)+

ΦU

(

k

),

(4)

2.2 滚动优化

基于上述预测推理，关键问题是在线滚动求解控制序列

U

(

k

)。设式(3)

N

步预测轨迹

Y

与给定的期望轨迹

Y

差值最小，同时考量控制量能量最小的原则。目标函数表达如下：

J

=‖

Y

-

Y

‖

P

+‖

U

‖

Q

,

(5)

式中,

P

与

Q

为适当维数的权重系数矩阵;此处

P

、

Q

均为单位矩阵，权重矩阵用以表达不同分量在目标函数的重要程度。在本系统下，实际期望目标函数

J

为最小值，即为

minJ

。

为实现函数式(5)最小的目标，通常需要将其转化为对应的二次规划问题进行求解。根据凸优化理论，需要使得目标函数仅包含控制变量的解析式，对式(4)进行展开，转化成二次规划标准型：

(6)

根据标准二次规划问题的要求，将式(4)代入式(5)，保留与决策量

U

有关的，易得新的目标函数：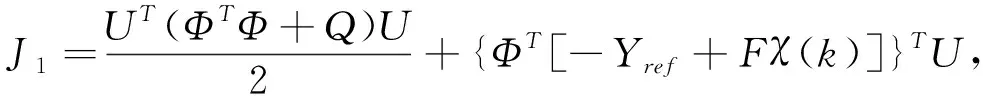

(7)

根据反应堆中棒速控制机理，控制棒的棒速上界为0.019 05

m/s

，故式(7)在求解过程中还应当添加二次规划的约束条件：|

u

(

k

) |<0.019 05,

k

=1,2,3,…,

N

。将其改写成线性不等式形式：

A

U

≤

U

,

(8)

2.3 反馈校正

中子探测器容易受到噪声干扰，中子密度检测的误差给功率控制带来了困难，同时也使得模型预测控制下预测模型与系统真实模型不能完全匹配。在上节的滚动优化方法中，可以获得控制时域

Nc

步的控制序列

U

向量的第一个控制信号

u

(

k

)，施加到有噪的反应堆对象中如式(9)所示。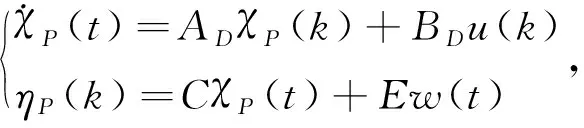

(9)

实际系统式(9)与预测模型式(2)的区别在于真实系统中增加了中子密度检测的噪声

w

(

k

)，这造成了预测模型与真实模型系统的不匹配。因为每时刻的输出量

η

(

k

)及实际的状态量

χ

(

k

)更新了预测模型式(4)，因此整个系统实际工作在闭环的模式下。更新的输出量

η

(

k

)实际是

δn

，它会将系统迁移至新的平衡点

n

(

k

)，式(9)的输出方程可以得到噪声

w

(

k

)，也将直接影响系统的平衡点，因此在实际系统应用中，该噪声不能被忽略。

2.4 控制算法综合

根据以上模型预测控制的原理，算法流程如图2所示。在反应堆的模型预测控制中，实际是预测模型(理想无噪)与有量测噪声的物理模型之间的状态量与平衡点的流转，并通过接近真实模型的预测模型求解控制量来实现跟踪参考轨迹

Y

。

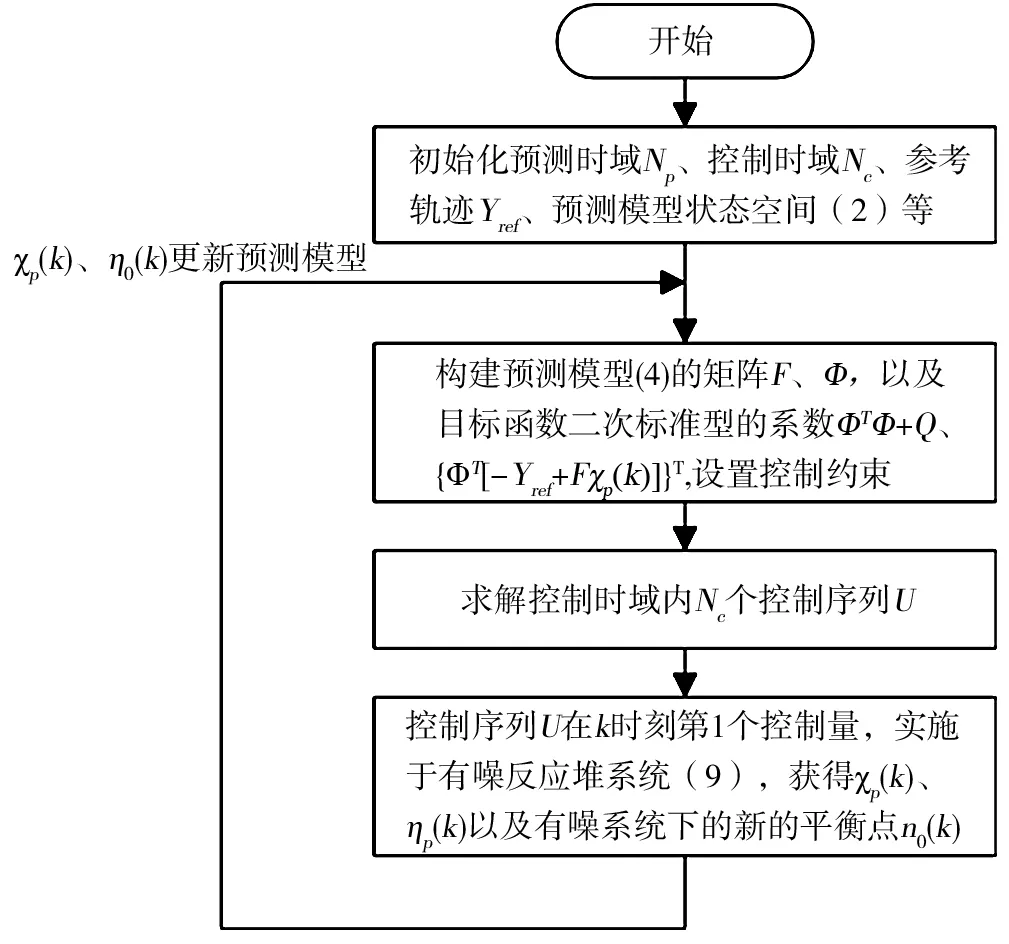
图2 具有量测噪声的反应堆模型预测控制算法

预测模型式(4)与有噪系统式(9)两者虽然有差异，但是由于量测噪声通常是均方为0的白噪声(即期望

E

{

w

(

k

)}=0)，利用预测模型式(4)生成的控制序列对实际有噪系统式(9)进行控制，可以达到期望的控制效果。

3 仿真实验及分析

利用MATLAB平台使用模型预测控制对有噪系统式(9)进行仿真研究，同时与PID控制算法进行对比。鉴于模型预测算法的目标是实现目标优化函数最小，其在轨迹追踪、控制量能耗等性能方面优于PID控制算法。下面通过仿真实验进行验证说明。

模型预测控制算法的预测时域的步长

N

与控制时域

N

步长分别选为25和8。权重系数

P

、

Q

均为适当维数的单位矩阵，保证权重平均。仿真过程设置初始中子密度

n

为0.50,即为50%

P

，功率变化轨迹为50%-70%-60%，噪声信号

w

(

k

)(见图3)为[-0.05%,0.05%]的额定功率区间。在轨迹变化过程中，参考曲线以1%额定功率每秒的速率实现递增或递减，模型预测控制跟踪参考轨迹的效果图如图4所示。对应相同噪声情形和状态初值，使用PID控制方法，选择对应的一组PID参数为：

k

=0.55;

k

=0.07;

k

=0.9，控制效果如图4所示。

图3 期望为0的噪声w(t)序列 图4 MPC与PID响应参考轨迹曲线图

噪声

w

(

k

)范围为[-0.05%,0.05%],整体变化范围为0.1%，但是其变化对应的功率增量变化范围为

ΔP

=0.1%*

P

=2.5 MW,此功率增量

ΔP

是较大的，但是闭环控制是基于中子探测器的探测结果(中子密度

n

)进行输出，对于中子探测器相应的误差是常见的，所以考虑该噪声信号是有实际意义的。

由图4可知，PID控制策略整体能够实现闭环非线性的反应堆控制系统的轨迹跟踪，但是效果要远低于MPC的控制策略；MPC模型预测控制策略在整体上完整跟踪了系统参考轨迹，同时，在噪声影响下，其超调量也远低于PID控制策略。

为了进一步分析两种控制效果，其余4个状态量(

δ

,

δT

,

δT

,

δρ

)偏离各自平衡点的轨迹分别如图5、图6、图7、图8所示。从图5～图8中可以看出，虚线所展示的PID控制效果变化剧烈程度均高于MPC控制算法。同时可以观察到整个反应堆的反应性在PID控制策略下，动态范围整体较大，而MPC控制策略下，其反应性变化较为平缓，纵观整个状态量的控制性能可以得出MPC算法控制效果较优异。

图5 MPC与PID的先驱核浓度 图6 MPC与PID的燃料平均温度

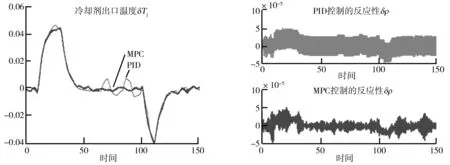
图7 MPC与PID的冷却剂出口温度 图8 MPC与PID的反应性

在模型预测控制的优化函数中，同时约束了控制量的能量，即在控制能量有界的情形下，其控制能量应当代价最小,PID与MPC控制算法的控制信号

u

(

k

)如图9所示。模型预测控制策略产生的控制序列

u

(

k

)(每次计算控制序列

U

中被实施的控制量)较PID控制算法的控制能量要小得多。

图9 PID与MPC控制算法的控制信号u(k)

4 结论

从代表功率水平的中子浓度的量测中误差的实际出发，MPC控制策略应用无噪的预测模型，也能做到优异的轨迹跟踪效果。对比MPC与PID不同的控制策略，模型预测控制因其聚焦了轨迹误差最小与控制能量最低的目标函数，其功率轨迹跟踪、控制信号

u

(

k

)的性能均优于PID的控制策略，但是在线计算控制序列，造程计算繁杂，同时产生的

N

步的控制时域的控制序列仅有第1个元素应用于控制系统，造成了一定的计算冗余。但总体而言，基于无噪声预测模型的MPC控制方法可以应用于有噪声(均方为0)的反应堆功率控制系统，并能获得较为优异的控制效果。