地质统计学在纳米比亚湖山铀矿床资源量估算中的探索应用

荣建锋，朱力

（1.中广核铀业发展有限公司，北京 100029；2.核工业北京地质研究院，北京 100029）

白岗岩型铀矿是纳米比亚在世界上独有的铀矿类型，纳米比亚湖山白岗岩型铀矿床（Husab Uranium Deposits）是继罗辛铀矿床之后在纳米比亚发现的又一个世界级特大型铀矿床，是21 世纪以来非洲乃至世界铀资源勘查领域新发现的最大铀矿，其资源量和产量均位居世界第3 位［1-2］，在全球占有重要位置。

将三维建模技术与地质统计学方法结合起来估算资源储量是当前矿产资源储量估算的发展方向［3］，但在国内矿产勘查中应用还不普及。由于湖山铀矿床资源量巨大，矿量集中，矿体主要呈似层状、脉状、透镜状，矿体数量多，利用传统的块段法估算资源矿体连接、圈定和计算繁杂，工作量巨大，周期长易出差错，利用地质统计学和专业矿业软件估算资源势在必行。2016 年以前，湖山铀矿床的资源量估算和更新均委托国外公司开展。2019 年，中广核铀业公司在完成湖山铀矿1、2 号矿带外围补充勘探的基础上，应用地质统计学和专业矿业软件Data Mine，首次自主开展资源估算，以验证湖山铀矿1、2 号矿体的资源量，并积累经验、培养队伍。本文以湖山铀矿北部的1号矿带（简称Z1）为例探讨地质统计法在资源量估算中的应用。

1 矿床地质特征和地质模型

湖山铀矿床发现于2006 年，通过约5×105m的钻探施工，控制了一条由1～5 号矿带组成、南北走向上长约8 km 的特大型白岗岩型铀矿带，其中Z1 矿体规模最大，资源量占整个矿床的近一半（图1）。湖山白岗岩型铀矿床大地构造上位于纳米比亚埃龙戈地区铀矿省的泛非达马拉造山带的南部中央区带，矿区出露主要地层自下而上有：前达马拉基底的阿巴比斯组杂岩体（Abbabis）、达马拉层序的艾杜西斯组（Etusis）、可汗组（Khan）、罗辛组（Rossing）、楚斯组（Chuos）、阿兰蒂斯组（Arandis）、卡里比布组（Karibib）和卡塞布组（Kuiseb）。含矿主岩为浅灰白色白岗岩，矿化岩体主要侵入罗辛组，极少量侵入可汗组内，矿体主要呈似层状、脉状、透镜状。

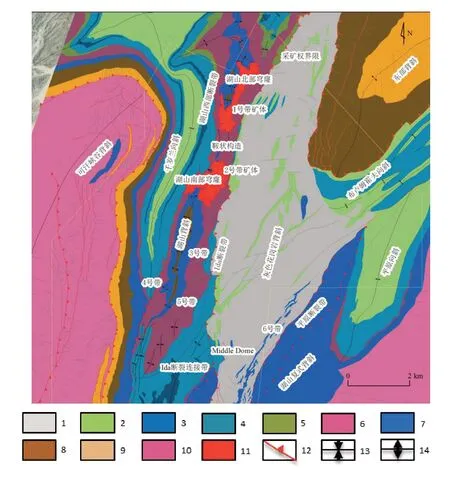
图1 湖山铀矿地层和构造示意图Fig.1 Schematic map of strata and structure in Husab uranium deposit

Z1 矿体主要侵入于湖山北部穹窿的东翼，走向28°，西翼走向355°，倾角为20°～55°。矿体主要产于罗辛组内，矿化白岗岩产状与地层一致，受地层控制明显，呈似层状、脉状和透镜状，总体成群脉状（图2）。

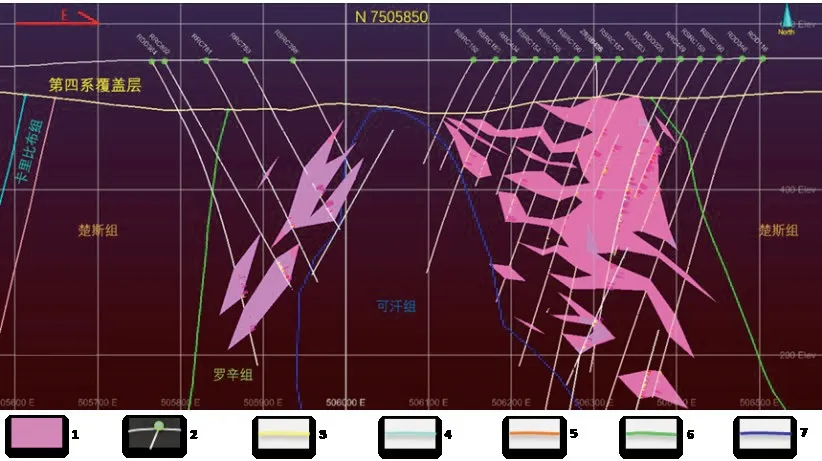
图2 Z1 矿体7505850 勘探线矿体解译剖面图Fig.2 Interpretation of Z1 ore body in section of exploration line 7505850

2 矿床数学模型的建立

2.1 数据库建立

本文以湖山铀矿床Z1 的铀矿体为资源量估算对象，区域化变量选取主要成矿元素U的品位。该变量来自于1 223 个钻孔，共260 236 个岩性编录数据，278 623 件样品分析结果，在Data Mine 软件中创建地质数据库，建立如下数据表。

孔位表：包括钻孔的孔口数据、钻探深度及钻孔类型等基本信息；

测斜表：包括钻探施工过程中的测斜信息；

岩性编录表：包括岩心/岩屑的岩性记录、地层代号等信息；

样品品位表：包括钻孔取样分析结果及其取样位置等信息。

2.2 矿体实体模型

在建立的数据库基础上，首先建立地层模型，然后按照工业指标将相邻工程对应的见矿部位用直线进行连接，圈定出剖面矿体解译线（图3）。根据剖面上矿体解译线，进入三维界面将相邻剖面对应的线框进行连接，在三维空间上形成矿体的实体模型［4］（图4）。实体模型直观地体现了矿体空间展布的几何形态，其内部包含的原始品位数据则是矿块模型估值的重要基础。

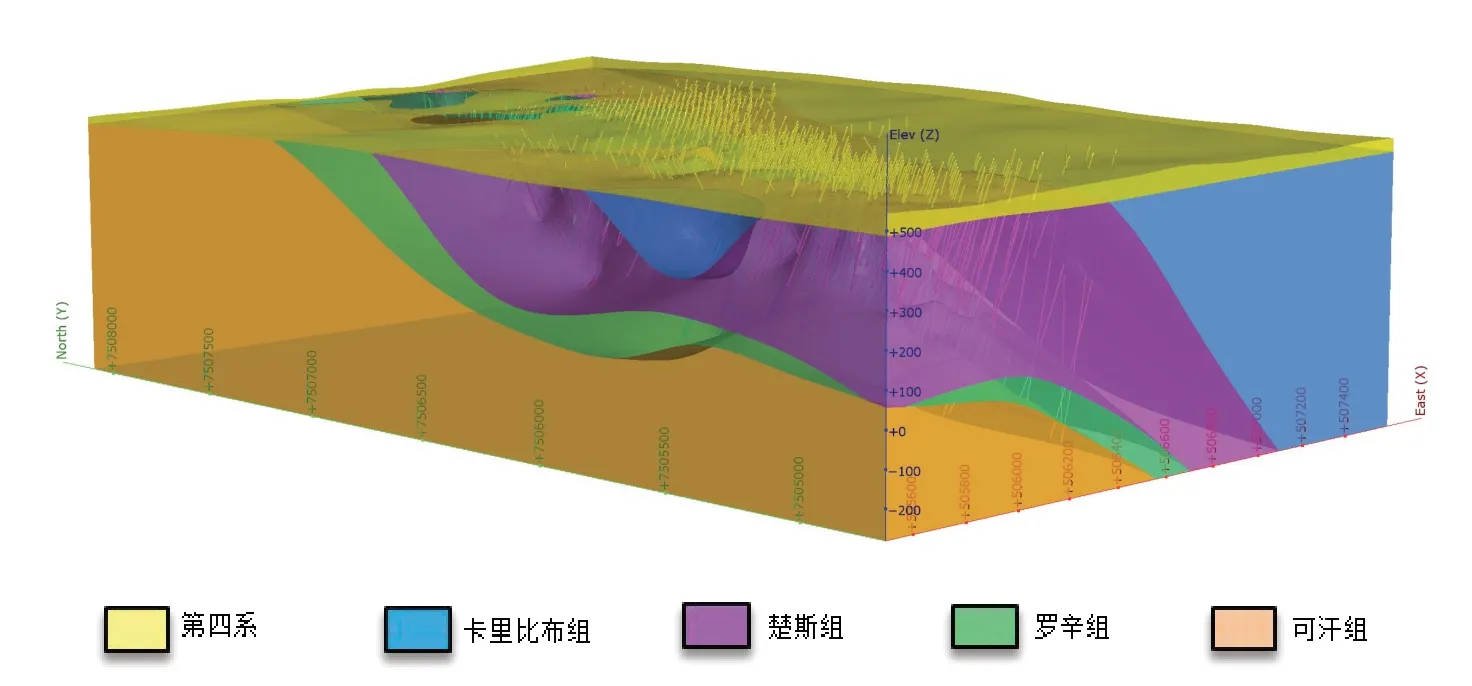
图3 数据库图形化文件（钻孔＋地层三维模型）Fig.3 Graphical database file（boreholes and strata model）

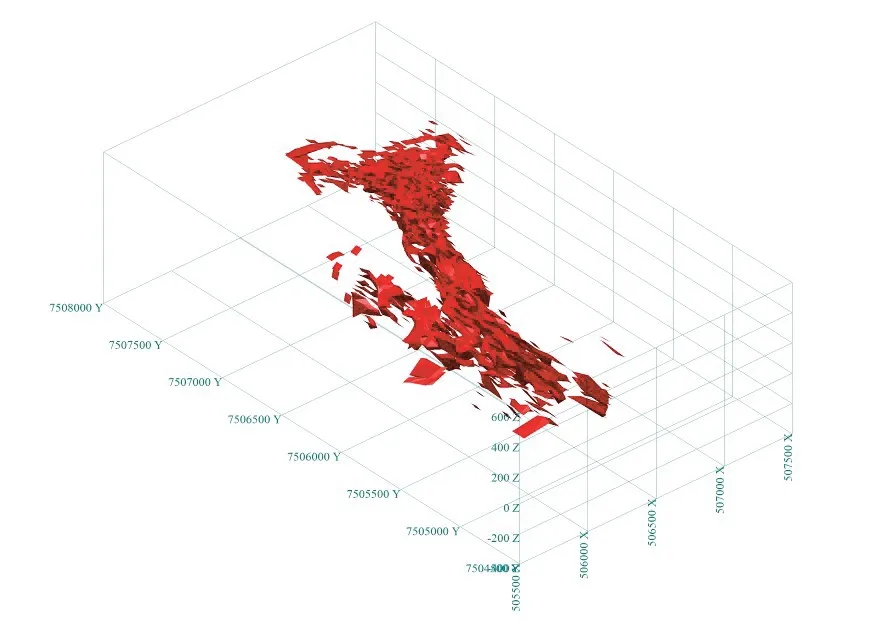
图4 Z1 矿体三维空间模型示意图Fig.4 Schematic 3D model of Z1 orebody

3 矿床数学模型的分析研究

3.1 特高品位识别和处理方法

特高品位的识别和处理是资源量估算中必须要考虑的步骤。传统的识别方法有3 种：采用品位均值的6～8 倍值作为特异值下限；将累积概率达到97.5%的样品品位值作为特异值下限［5］；侯景儒等曾提出根据样品品位的变异（化）系数来识别特异值，在不同的变异系数范围，选取不同倍数（2～20 倍）的均值作为特异值下限［6］。国际咨询公司地质师在进行特高样品的处理时，通常依据变化系数和西舍尔值来确定累积概率的分位值，一般选择矿体内品位数据的97.5%或99%分位数的数值作为特高品位的下限值。

经统计，在Z1 矿体中，样品品位最大值为243 618×10-6，平均品位为458×10-6，标准方差为1 654.3，品位变化系数为3.612，铀品位在矿体域中呈偏态分布，需要进行特高品位的处理（图5）。

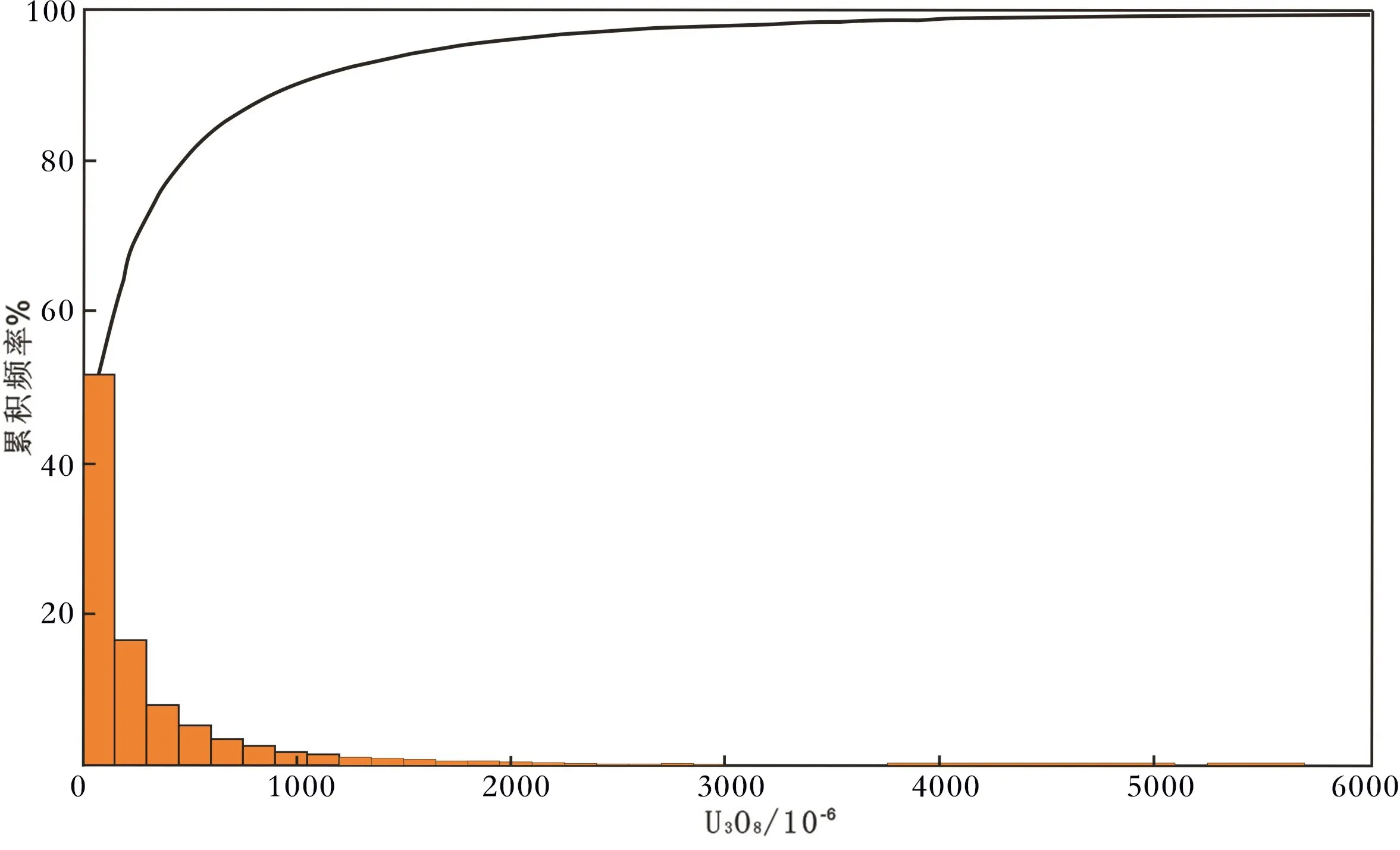
图5 Z1 矿体原始样品铀品位统计直方图和累积分布曲线Fig.5 Statistical histogram and cumulative distribution curve of uranium grade in Z1 orebody

结合累积概率曲线来看，铀品位大致在99%的分位数附近品位分布明显少，在6 000×10-6处对数累积频率曲线有明显的转折（图6）。按6 000×10-6下限值处理样品后，品位均值变化不大，品位变化系数从3.61 降至1.86，西舍尔值与平均值比较接近，标准差、偏度、峰度值也有大幅改善，故将6 000×10-6定为Z1 特异值的下限（表1）。

表1 Z1 矿体特异值处理前后矿化域内样品统计数据对比Table 1 Statistic of the samples and grade before and after outliers treatment in Z1 orebody

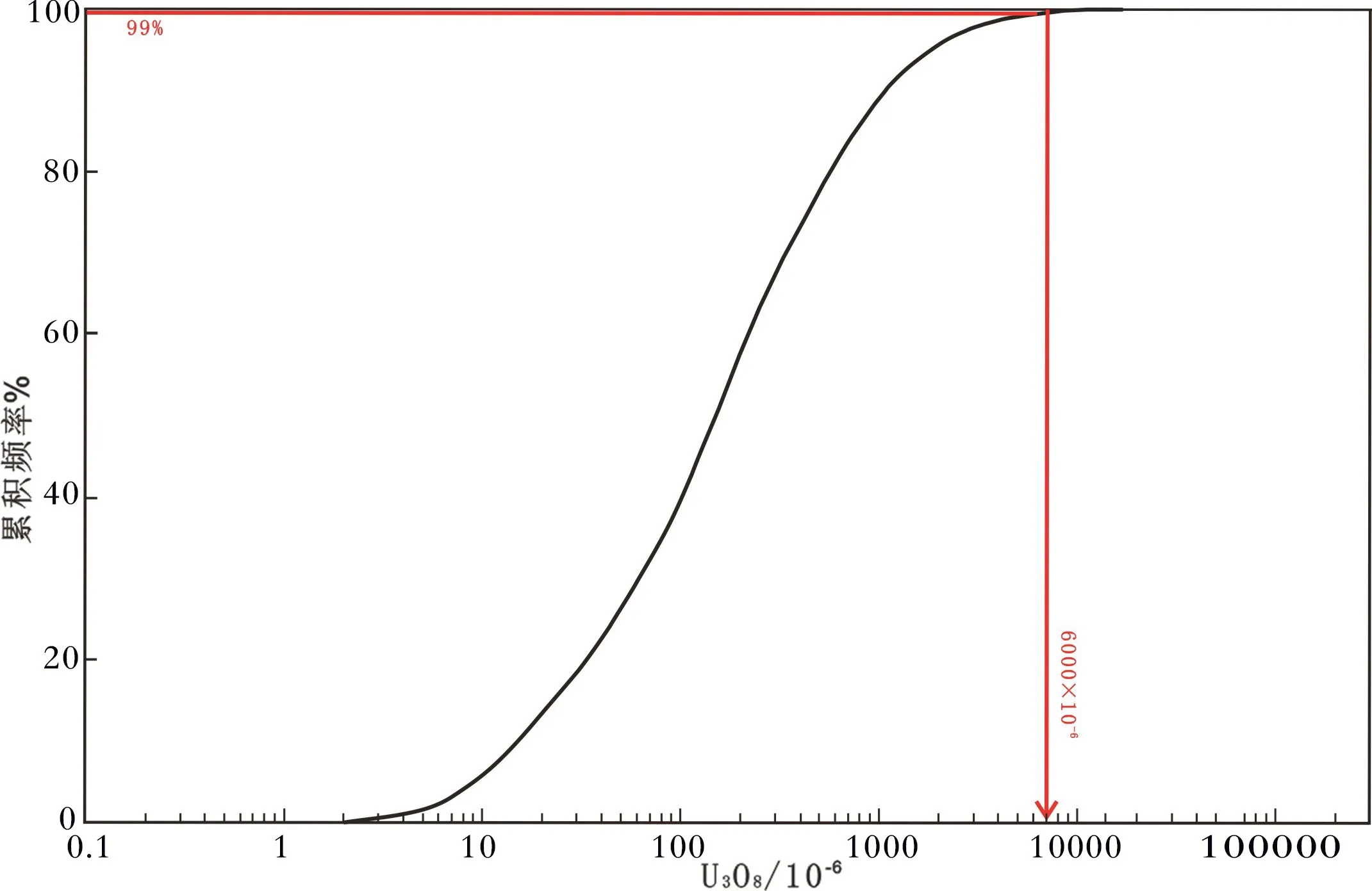
图6 U3O8品位累积频率曲线及截止品位Fig.6 The cumulative frequency curve of U3O8 and the top-cut grade

3.2 样品组合与统计分析

样品组合是将不等长的样品长度和品位统一到等长的样品上。根据地质统计学原理，为确保得到各参数的最优无偏估计量，所有的样品数据应落在相同的承载上，即同一类参数的地质样品段的长度应该一致［7-9］。因此，在估算之前，必须按照一定长度对长度不等的样品数据进行组合，并统计分析其分布特征。样品组合有多种方式，如按钻孔长度组合、按样品长度组合、按台阶高度组合、混合组合等［10］。经统计，Z1 矿体内含有样品72 053 件，平均样长0.82 m，1 m 样长占比65%，处理特异值后按组合样品长度分别设为1 m、3 m 进行统计和比较。两者的统计学分布特征，两种组合方案的样品特征基本不变，但是3 m 组合方案的变化系数、偏度和峰度值均有所降低，说明样品数据更符合地质统计学对参与估值数据的要求；且样品总数大幅减少有助于节省软件处理数据花费的时间。综上，判定3 m 样品组合是较优方案（表2）。

表2 Z1 矿体特异值处理后样品组合统计数据对比Table 2 Statistic of the composite grade after outliers treatment in Z1 orebody

对3 m 样品组合后的数据进行统计分析，获取U3O8样品的品位分布直方图呈正偏分布，对品位数据取对数后，样品基本呈正态分布，无明显的多峰分布特征，可以采用普通克里格进行品位估值（图7、8）。

图7 Z1 矿体组合样U3O8品位分布直方图Fig.7 Histogram of U3O8 grades in a composite sample of Z1 orebody

3.3 变异函数分析

在进行品位变异函数分析时，根据矿体产出特征，分别沿矿体走向（主轴）、倾向（次轴）、厚度（最小轴）3 个方向进行变异函数分析，从而确定各方向实验变异函数计算时角度及距离参数（表3）［11］。

表3 实验变异函数参数表Table 3 Parameters of experimental variation functions

3.4 结构分析

按照数据分析流程，需对区域化变量进行实验变异函数计算，在此基础上拟合出理论变异函数。借助结构分析可以更全面的掌握区域化变量的结构性和变异性，从而保证实验变异函数计算的精度。实验变异函数计算完成后，需选择合适的数学模型表达变异函数的曲线特征。用一个球状模型来表示各个方向的变异性，从而实现理论变异函数的拟合，这是业内广泛使用的方法［12］。

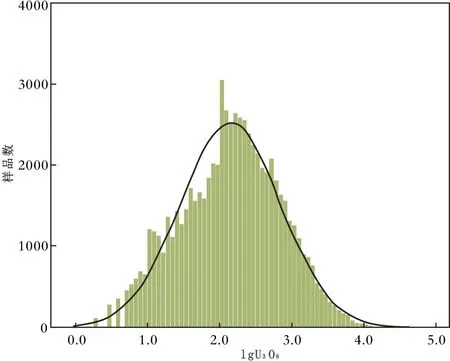
图8 Z1 矿体组合样U3O8品位对数值分布Fig.8 Logarithmic distribution of U3O8 grades in a composite sample of Z1 orebody

球状变异函数模型标准形式为：

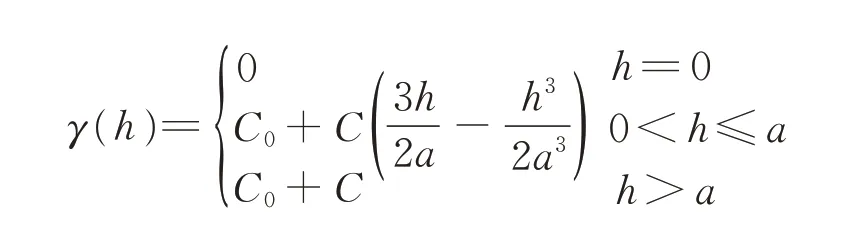
式中：γ（h）—变异函数；h—滞后距离；C0—块金常数；C—跃迁常数；C0+C—基台值；a—变程［13］。

根据矿体空间赋存特征，结合成矿规律研究成果，使用Data Mine 的分析模拟功能调算各种参数，最终得到矿体走向、倾向、厚度方向变异函数拟合曲线（图9）。所拟合出的球状模型理论变异函数最佳结构参数见表4。

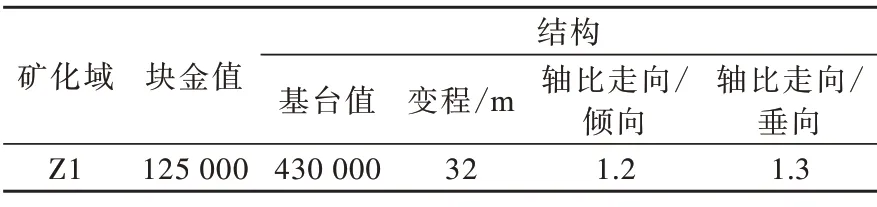
表4 Z1 矿体最佳理论变异函数结构参数表Table 4 Main parameters of the best variogram of Z1 orebody

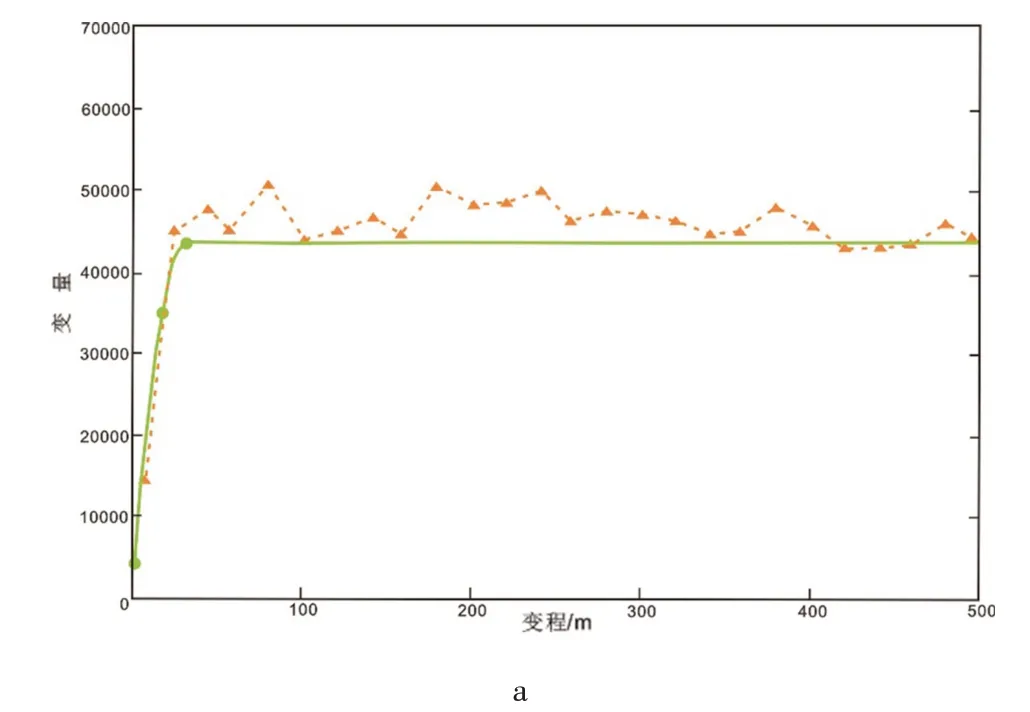
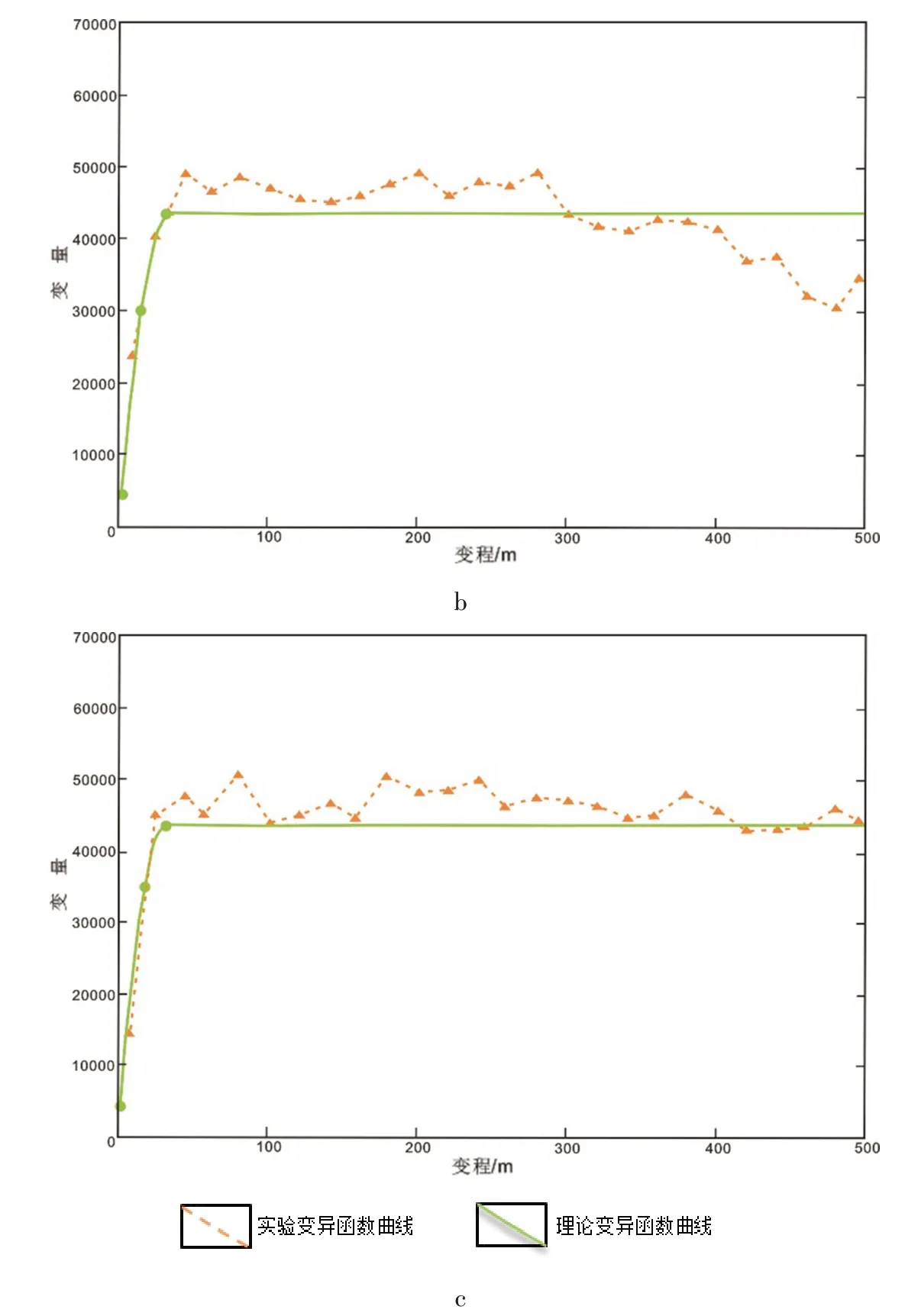
图9 Z1 矿体三维方向变异函数曲线Fig.9 The variogram of grade in 3D of Z1 orebody

3.5 理论变异函数交叉验证

在进行理论变异函数的拟合后，用交叉验证的方法对模型设置的参数进行检验。交叉验证的统计结果显示，均值差较小接近0，且方差/标准差趋近于1，良好的交叉验证结果证明变异函数结构模型可靠［14］，可作为普通克里格估值的参数（表5）。因此，前面分析得到的理论变异函数参数是可靠的，可用于该矿床U3O8品位估算。

表5 各项异性变异函数参数的交叉验证结果Table 5 Results of cross validation of each hetero variogram parameters

4 资源量估算

4.1 矿块模型的建立

在确定单元块尺寸时主要考虑采矿方法、最小开采单元大小、矿体形态、勘探线网度、最小可采厚度、夹石剔除厚度以及运算效率等因素［15］。该矿床采用露天开采方式，最小采矿台阶高7.5 m，设定单元块尺寸为12.5 m×12.5 m×7.5 m，在矿体边缘部次级块设为6.25 m×6.25 m×2.5 m。

4.2 矿块模型估值

矿块模型估值就是求出块模型中每个块中心位置的品位值，这就需要在具有相关性的空间范围内搜索已知点，并通过给予一定的权系数实现“最佳、线性、无偏”估计［16］。本次工作采用普通克里格法分三次进行估值，完成估值后的块体模型可以在三维空间详细列示不同品位级别的矿石的分布情况（表6，图10）。

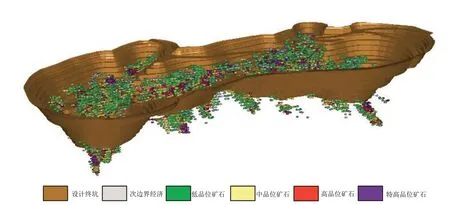
图10 Z1 矿体品位估值块体模型图Fig.10 Block model diagram of Z1 orebody

表6 Z1 矿体椭球体参数表Table 6 Parameters of search volume of Z1 orebody

4.3 可靠性验证

为验证估值品位与原始数据的一致性，开展全局检验统计分析两组数据在三维空间分布特征是必要的。Swath 曲线就是用于刻画在特定方向上样品与估值模型品位的吻合情况。本 文从X 轴、Y 轴 和Z 轴3 个方 向，分别 对 比 样品品位曲线和估值模型的曲线的品位变化趋势（图11）。整体而言，两组品位曲线较为一致，只是在矿体两端尖灭部位有较明显的偏差，这是由于样品数量较少，以及克里格估值方法在估值过程中产生的平滑效应引起的。

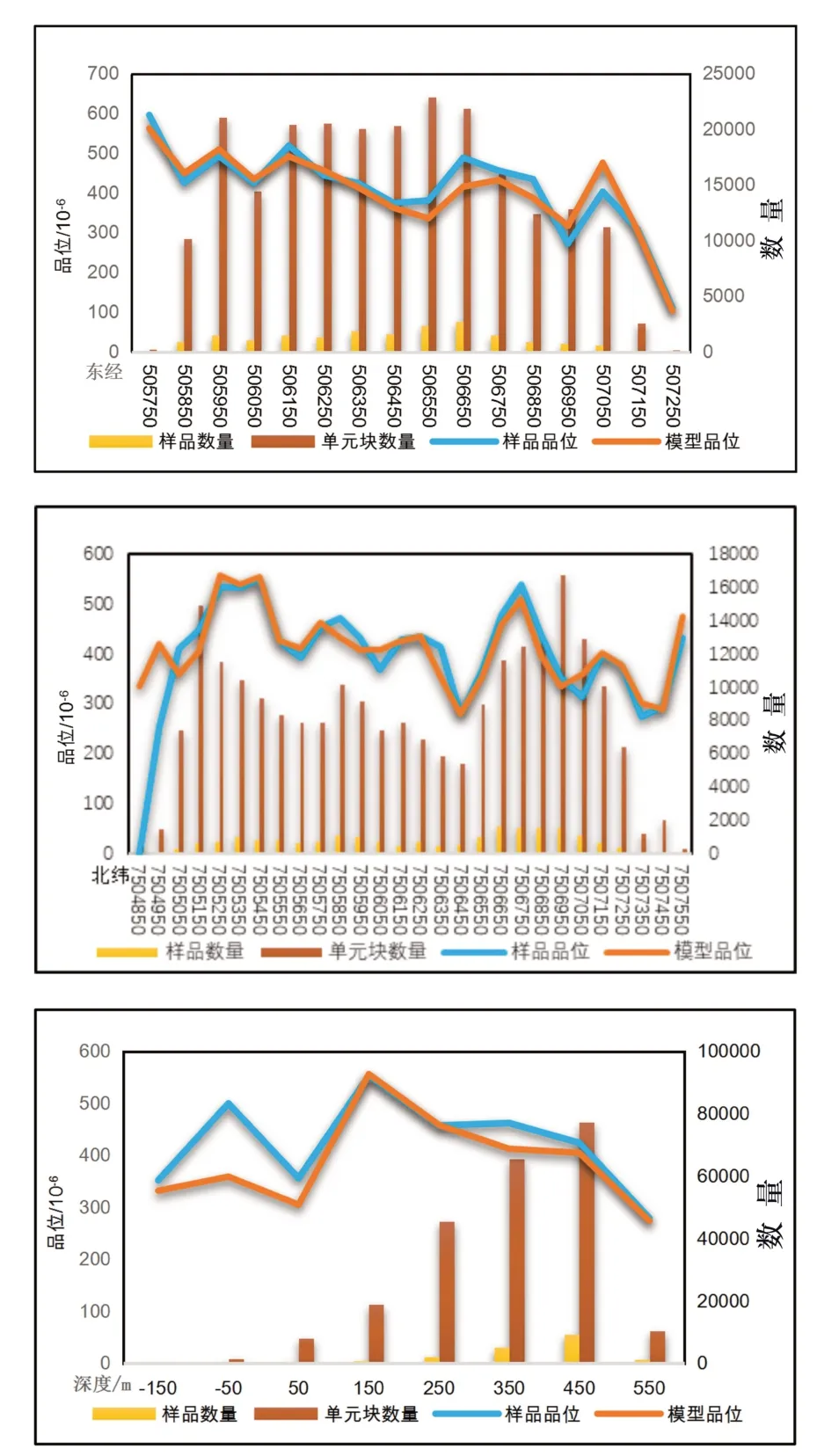
图11 Z1 矿体全局检验Swath 曲线对比图Fig.11 Swath plot of global inspection of Z1 orebody

同时，将矿体内等长组合样品的品位均值与估算品位均值进行比较，评估平均品位的变化，验证估值过程是否存在明显的偏差，从而实现对估算结果的可靠性验证。统计结果表明，块体模型中估值元素经过插值，品位产生平滑效应，平均品位有所降低（表7）。矿体等长样品位均值与块体品位插值均值比为92%，说明数据插值拟合度较高，没有明显偏差。

表7 矿体等长样品位统计与矿块体模型品位统计对比表Table 7 Statistics of samples and interpolation grade

为保证估值质量，本次工作还采用距离幂次方反比法对Z1 资源模型的工业矿部分进行资源量估算结果验证。经对比，两种估算方法的矿石量相差1.5%，平均品位相差1.5%，金属量相差0.2%。两种估算方法的矿石量、金属量及品位相差均在5%以内，说明本次研究采用Data Mine 软件普通克里格法估算资源量是适当的，估算结果是可靠的。

与2012 年资源量估算结果进行对比，Z1 矿体的控制级以上资源量减少5%，推断级资源量也有一定程度的减少，本次工作达到了资源量核实的目的。

5 结论

本次研究综合运用地质统计学理论，在Data Mine 矿业软件平台上建立了纳米比亚湖山铀矿床的数学模型，在研究和处理特高品位数据的基础上，使用球状模型计算和拟合了不同方向实验变异函数并进行了结构分析，成功构建出符合矿床地质特征的结构模型，交叉验证各结构参数合理可靠；最后采用普通克立格法对铀矿石品位及矿石量进行了估算。可靠性验证及对比结果表明，本次研究所选用的区域化变量和模型估值方法合理，符合矿床空间展布特征和分布规律。地质统计学理论和Data Mine 矿业软件在资源量估算中快速、动态和直观的特性得到充分体现，其成果可用于矿山资源评估、露天采矿设计以及生产计划编制等工作。