基于GM-HMM的驾驶人疲劳状态检测

张 明 恒，刘 朝 阳，郭 政 先，万 星

(1.大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024；2.大连理工大学 汽车工程学院，辽宁 大连 116024 )

0 引 言

驾驶疲劳是交通事故致因的重要组成部分，当前针对驾驶人状态检测的车载系统研发已经成为人们关注的焦点问题[1]．从驾驶疲劳检测的过程来看，其本质在于利用构建的特征-状态模型对驾驶人疲劳状态进行实时评估．其中，疲劳特征的选择应能满足车载系统需求，检测模型应体现驾驶疲劳的动态特性．

目前，应用于驾驶疲劳检测的特征指标主要包括车辆运行特征、驾驶人表观特征和生理特征[2]．其中，基于车辆运行特征的方法可以充分利用车辆运动信息，具有较好的实时性，但易受驾驶习惯等因素影响[3]；基于驾驶人表观特征(如PERCLOS)的方法，其特征获取大多采用非侵入式的视觉传感器，具有灵活的平台适应性和成本优势，已逐渐成为舱内感知技术(ICS)领域的主流研发方向[4]；基于驾驶人生理特征(如脑电(EEG)信号)的方法，由于其可以直接反映疲劳变化，在疲劳发生初期即具备较好检测效果，常常被称为疲劳检测的金标准，但是由于其需要测试仪器与人接触测量，容易对驾驶人造成干扰，因此常常被用于其他检测方法的对标性测试[5]．

在疲劳状态检测模型研究方面，主要包括支持向量机(SVM)、神经网络、贝叶斯网络和隐马尔可夫模型(HMM)等．Hu[6]基于EEG数据搭建了SVM驾驶疲劳辨识模型，在对数据进行特征提取后有效提高了辨识准确率，但该模型仅在小数据量时准确率较高．为深入分析疲劳特征与疲劳状态间的映射关系，胡淑燕等[7]选用朴素贝叶斯网络建立了疲劳辨识模型，但疲劳的动态时序特性并未得到充分反映．针对疲劳的强时序特性，Fu等[8]基于HMM提出了一种疲劳检测方法，表现出了较好的检测效果．

综上，基于机器视觉等的驾驶人表观特征疲劳检测方法由于其自身优势逐渐成为应用研究的主流，而在建立相关特征与疲劳状态映射的过程中，准确的疲劳状态界定对其模型构建准确性具有重要影响，同时也是目前相关车载系统研发所面临的共性问题．因此，本文基于疲劳生成的强时序特性和输入数据的连续性，利用EEG数据构建一种高斯混合隐马尔可夫模型(GM-HMM)进行驾驶疲劳状态评估，为相关车载系统研发提供必要的驾驶疲劳状态比对参考．

1 驾驶疲劳检测机理

1.1 疲劳特性及检测模型

文献[9]表明，驾驶人疲劳状态的产生是一种随时间变化逐渐形成的过程．在驾驶过程初期，疲劳程度的增加与驾驶时间近似成线性关系；随着驾驶时间增长，疲劳程度将呈现不稳定的波动状态，如图1所示，其中横坐标t为驾驶人的持续驾驶时间，纵坐标F(t)为驾驶人的疲劳程度．由此可见，强时序性是驾驶疲劳形成的本质属性，用于驾驶疲劳辨识的基本模型应能反映这一基本特征，这也是提高相关识别系统准确性的关键．

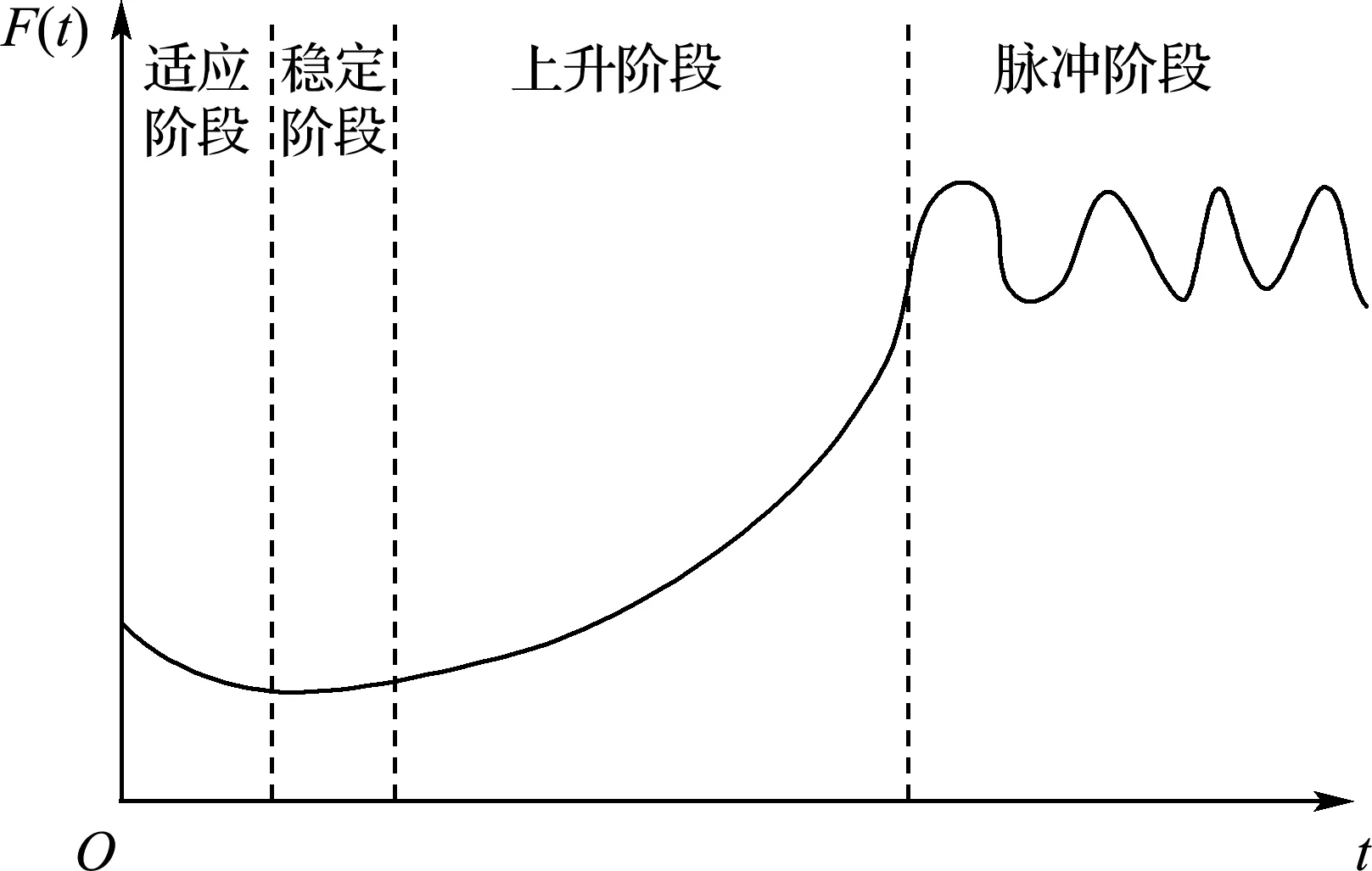
图1 驾驶疲劳-时间变化特性Fig.1 Driving fatigue temporal sequence characteristic

基于本文研究目的，生理特征参数EEG信号被用于HMM构建过程的基础数据来源，从而形成对疲劳状态水平的准确评估．同时，考虑离散型HMM虽然在实时性方面具有一定优势，但相对于连续型模型在准确度方面还有一定差距，因此本文采用高斯混合(GM)模型对HMM中的疲劳状态分布进行合理估计，以获得准确的疲劳状态辨识结果．本文的整体模型研究框架如图2所示．

图2 基于GM-HMM的驾驶疲劳辨识框架Fig.2 Driving fatigue detection framework based on GM-HMM

1.2 数据处理平台概述

本文基于ErgoLAB人机环境同步平台进行相关实验数据的采集和同步．数据采集平台由舱内感知设备、数据同步系统、状态标记过程组成．其中，舱内感知设备由BBT-E08-AAB007脑电仪和Logitech Webcam C930e摄像头组成．脑电仪被用于采集驾驶人脑电数据，摄像头被用于采集驾驶人实时图像；ErgoLAB数据同步平台可以在模拟驾驶时同步协调及汇聚脑电仪和摄像头采集的数据；状态标记过程是通过驾驶人状态自述和专家状态评估[10]获得当前时刻所对应的疲劳状态标签．实验数据采集平台的构成如图3所示．

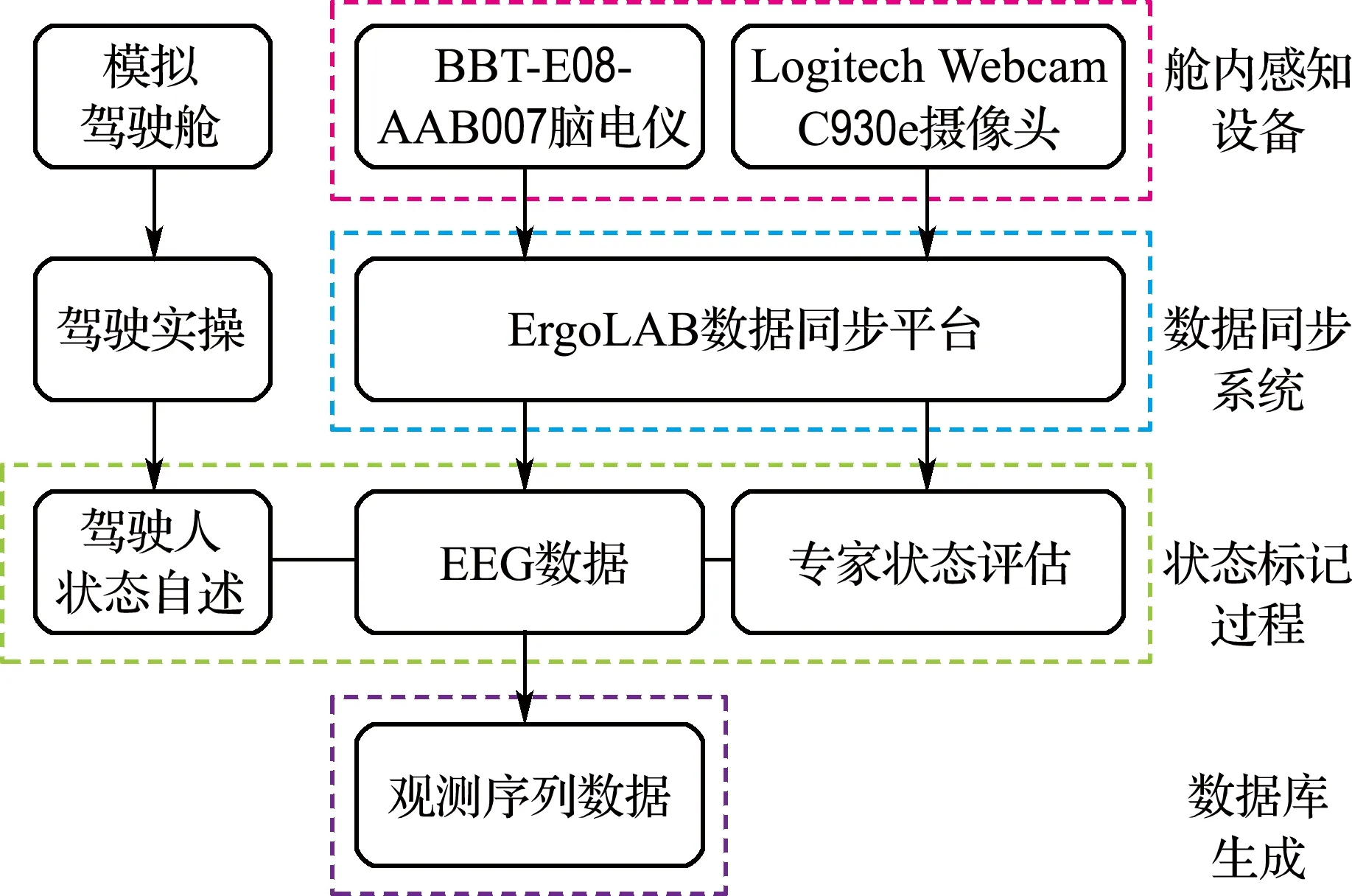
图3 ErgoLAB实验数据采集平台Fig.3 Experimental data acquisition platform based on ErgoLAB

在得到上述初始EEG数据库后，需要对其进行预处理(如滤波、去伪迹、降采样等)以获得准确的模型输入特征．预处理主要包括两个部分：基于小波包变换的特征提取操作和基于灰色关联分析的指标优选操作．基于小波包变换的特征提取操作是通过节律波重构来获取脑电仪每个电极通道的能量比值[11]；基于灰色关联分析的指标优选是将能量比值和疲劳状态进行关联性分析来找出与疲劳状态相关性最大的能量比值[12]．数据预处理的整体流程如图4所示．

图4 EEG数据预处理流程图Fig.4 The flow chart of EEG data pre-processing

2 基于GM-HMM的疲劳检测

GM-HMM的构建，总体上可分为两部分：GM拟合参数的确定和HMM的参数训练[13]．其中，由于EEG的数据符合正态分布，从而选择高斯拟合函数为概率密度函数，对观测数据进行拟合训练来确定GM的参数；根据驾驶疲劳生成的时序特性，选用各态遍历型HMM作为检测模型构建的基本结构，利用Baum-Welch和Viterbi 算法训练HMM完成最终参数的确定，其中模型λ的主要参数为(π，A，B)，π表示初始状态概率向量，A表示状态转移概率矩阵，B表示观测概率矩阵．

2.1 观测序列的GM拟合

脑电仪采集的EEG数据为离散数据，这会导致大量关键信息的丢失，要同时获得具有时序性和连续性的分析模型，方法之一是对观测EEG数据进行GM拟合．实际应用过程中，根据中心极限定理，大量观测EEG数据服从几个正态分布的叠加，图5展示了部分EEG数据的分布情况，其中横坐标n为数据片段数量，纵坐标G为EEG数据和高斯拟合数据的数值．

图5 EEG数据GM拟合曲线Fig.5 GM-fitting curves of EEG data

故本文利用高斯概率密度函数对观测序列拟合来确定HMM的参数：观测概率矩阵B=(bj(ot))N×R，其中N代表所有可能的状态数目，R代表所有可能的观测数目．观测序列的高斯概率密度拟合函数为

(1)

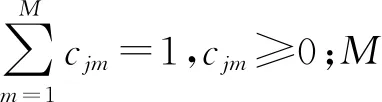
(2)

HMM的模型参数B决定了模型的收敛速度，且对后续模型的训练效果影响较大．本文采用K-means结合Viterbi算法对参数进行初始化，当模型收敛到更新值基本无变化时，说明达到了GM的拟合效果，此时将参数输出．观测序列的GM拟合具体流程如图6所示．

图6 GM拟合观测数据流程图Fig.6 The flow chart of GM fitting observation data

2.2 疲劳检测模型构建

基于本文研究目的，设S=(s1s2…sN)是驾驶人所有可能的隐状态集合，以时间刻度表示时，对应于长度为T的状态序列Q=(q1q2…

qT)；V=(v1v2…vR)是所有可能的观测状态集合，以时间刻度表示时，对应于长度为T的观测序列O=(o1o2…oT)．鉴于驾驶疲劳的时变性，其符合各态遍历型的HMM基本结构类型，本研究所用的HMM结构类型如图7所示．

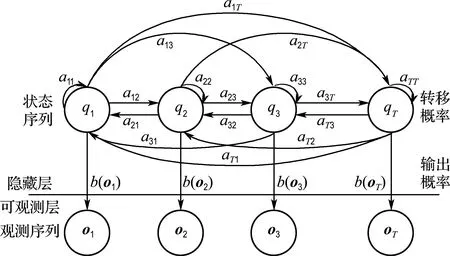
图7 各态遍历型HMM结构Fig.7 The structure of ergodic HMM

基于HMM模型算法，其前向变量α可定义为

αt(i)=P(o1，o2，…，ot，qt=si|λ)；i=1，2，…，N

(3)

后向变量β定义为

βt(j)=P(ot+1，ot+2，…，oT|qt=sj，λ)；j=1，2，…，N

(4)

其中αt(i)表示在HMM模型λ下，到时刻t为止产生的EEG数据观测序列为o1，o2，…，ot，且t时刻清醒(或疲劳)状态为si的概率．而βt(j)表示在HMM模型λ和t时刻疲劳或(清醒)状态为sj情况下，t时刻后产生EEG数据观测序列为ot+1，ot+2，…，oT的概率，T为总的时间序列．

由式(3)和(4)，在t时刻HMM模型λ中的清醒(或疲劳)状态si转移到t+1时刻的疲劳(或清醒)状态sj的概率公式为

ξt(i，j)=P(qt=si，qt+1=sj|O，λ)=

(5)

在t时刻为清醒(或疲劳)状态si的概率公式为

(6)

当初始参数确定好之后，利用Baum-Welch和Viterbi算法来估计HMM的最终参数．根据式(5)和(6)由Baum-Welch算法推导的HMM的参数π=(πi)N、A=(aij)N×N、B=(bj(k))N×R表示如下：

πi=P(q1=si)

(7)

(8)

(9)

式中：πi为t=1时驾驶人处于状态si的概率，i=1，2，…N，j=1，2，…，N，k=1，2，…，R；π表示初始状态概率向量；aij表示状态转移概率；bj(k)表示在t时刻驾驶人处于状态sj的条件下，生成第k个观测序列vk的概率．由于在训练过程中参数B会改变，需要对其内部参数进行重新估计．而在更新迭代参数π、A时会同时更新B，即同时更新GM模型中的cjm、ujm、Ujm3个参数．为方便表达，引入公式：

(10)

其中γt(j，m)表示在t时刻疲劳检测状态为sj且EEG数据观测序列是由第m个高斯混合函数拟合的概率，因此由式(10)可得其他参数更新的重估公式为

(11)

(12)

(13)

训练完成后，得到cjm、ujm、Ujm对应的最优参数c、u、U，最终所构建的GM-HMM驾驶疲劳检测模型可被表述为

λ=(π，A，c，u，U)

3 实验验证

3.1 实验设备及流程

所需观测序列数据由实验获得，以东风菱智汽车驾驶舱为主体进行实验环境搭建，实验时驾驶人佩戴脑电仪，按高速公路的行车场景视频进行对应的模拟驾驶操作[14]；同时驾驶人的行为和状态被摄像头采集成视频数据，由ErgoLAB数据同步平台保证EEG信号与视频数据同步采集．所用实验设备如图8所示．

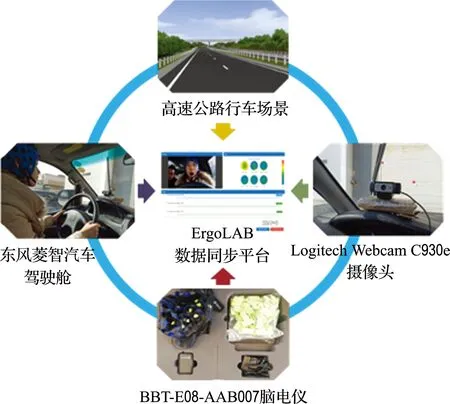
图8 实验环境和设备Fig.8 Experimental environment and equipment

为保证实验过程采集数据的有效性，实验前以问卷形式对驾驶人进行了作息时间规律的调查，并结合调查结果选择驾驶人容易出现疲劳状态的时段进行了相关实验．驾驶人的选取充分考虑了年龄、驾龄等因素，共招募10名具有一定驾驶经验的驾驶人，同时为进一步避免相关外部因素对驾驶人的影响，所有驾驶人被要求在实验前一天不得饮食含提神作用的食品、不能服用药物以及做剧烈运动等．实验时间选取在易发生驾驶疲劳的13：00～15：00，实验场景选取为环境变化较为单调的道路，并通过驾驶人的行为特征和主观报告来验证驾驶人在实验时进入深度疲劳驾驶状态．实验电极位置选取为Fpz、F3、F4、Fz、C3、C4、P3和P4，采样频率为256 Hz；在脑电信号采集的同时，由工作人员每隔5 min询问并记录驾驶人的当前状态，作为疲劳状态主观评分．

实验结束后，对照视频采集数据将由干扰因素(如接听电话、喝水等)影响的异常状态EEG数据段剔除，通过专家经验认定疲劳观测指标与实际状态的对应标记．为确保评价准确性，将视频对照的专家评分与驾驶人自述的主观评分进行综合分析来确定驾驶人的最终真实状态，最后将每位驾驶人的真实状态与其EEG信号数据段对应标记来构建初始数据库．图9是剔除异常数据并进行状态标记后的驾驶人状态时序图，其中横坐标为驾驶人的驾驶时间，纵坐标为参试驾驶人的编号．

图9 驾驶人状态时序图Fig.9 The temporal sequence diagram of drivers′states

由于实验过程中的EEG数据掺杂有噪声伪迹，如心电、肌电、眼动(EOG)等生理性伪迹，必须对原始EEG数据进行相应的预处理[15]．本文所采取的预处理方法如表1所示．

表1 预处理方法Tab.1 The pre-processing methods

3.2 特征指标优选

EEG原始信号的维度较高，疲劳特征表现不明显，因此需要从预处理后的EEG数据中提取出最能表征驾驶疲劳的特征指标，其中能量比值指标可有效表征出驾驶人的疲劳状态[11]．本文首先利用小波包变换进行节律波的频率分解来提取能量特征，由于Daubechies小波的灵敏度高、正则性好，且其中的db4小波与EEG信号的波形最为相似，故选取db4小波作为分解小波基．EEG信号频率范围为0～30 Hz，常用4种波形频带为δ(0～4 Hz)、θ(4～8 Hz)、α(8～12 Hz)、β(12～30 Hz)，故对EEG信号进行第一层节点选取为0～64 Hz的5层小波包分解．分解后的4种节律波如图10所示，其中横坐标n′表示经降采样后数据点的序列，纵坐标A为对应数据点处经小波包分解后的幅值．

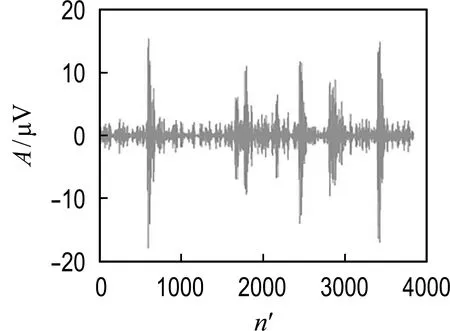
(a)α信号波形

小波包分解系数可以反映EEG数据中时域和频域的信号能量分布，因此可以利用小波包分解系数平方的叠加来表示信号的能量，节点能量计算公式为

(14)

其中pi(t)表示在t时刻第5层分解上的第i个节点的小波包分解系数，i=0，1，…，15．因此各节律波的总能量计算公式为

(15)

其中r表示α、β、δ、θ4种节律波，k的范围由节律波r的节点数决定．由式(15)，将4种节律波的能量值进行快波与慢波的比值[16]计算，得到8种能量比值特征指标，其公式为

(16)

EEG信号的8种特征指标与驾驶人的疲劳状态存在潜在对应规律，可以利用灰色关联分析(grey relation analysis，GRA)探寻与疲劳状态关联最大的指标[17]．以驾驶人的实际状态为参考数列，以8种EEG指标为比较数列进行关联度比较，结果如图11所示，其中横坐标为8种EEG特征指标，纵坐标RGRA为8种EEG指标分别与实际状态参考数列的关联度值．

图11 关联度数值图Fig.11 Numerical graph of relation degree

从图中可以看出F5指标的相关性最大，F8次之，符合随驾驶疲劳程度加深数值呈上升趋势；F3与参考序列最不相关，符合随疲劳程度加深数值呈下降趋势．因此，用于本文研究的驾驶疲劳优选特征向量F组成为

F=(F3F5F8)

3.3 实验结果及分析

将前8名参试驾驶人测试得到的特征数据指标按照驾驶人清醒、疲劳两个状态进行分类，作为训练集数据按照第2章方法构建了驾驶人清醒模型和驾驶人疲劳模型．为验证本文所建立模型的性能，将最后一名驾驶人的特征数据作为测试数据，利用前向后向算法最大概率地对模型匹配后，将数据输入到对应GM-HMM中进行状态检测，识别流程如图12所示．

图12 驾驶人状态识别流程图Fig.12 Driver state detection flow chart

图12中λa和λf分别对应清醒、疲劳检测模型．将驾驶人的部分实验数据作为测试序列输入到搭建的GM-HMM中，得到了实际状态和模型识别结果的对照，如图13所示，其中横坐标为驾驶人的驾驶时间，纵坐标为驾驶人的疲劳状态S(S=0代表驾驶人处于清醒状态，S=1代表驾驶人处于疲劳状态)．

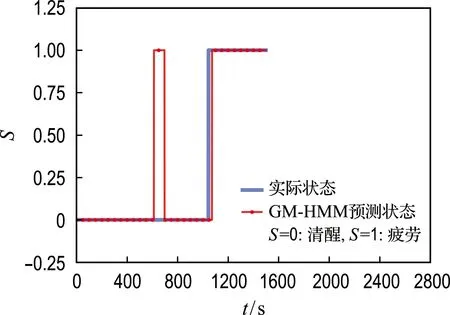
图13 GM-HMM预测结果Fig.13 Prediction results of GM-HMM

从图13中可以看出，本文所构建的GM-HMM在驾驶初期表现出了很好的检测判断效果；在驾驶中期可能由于驾驶人分心等原因(但不是疲劳)存在部分错误判断；在产生驾驶疲劳后表现出了优良的检测效果．因此，在考虑疲劳状态时序性和观测序列连续性因素后，本文所建立的GM-HMM可进行有效的驾驶疲劳状态辨识．

为进一步对比时序性和HMM内部参数连续性对疲劳状态辨识准确率的影响，设置离散隐马尔可夫模型(DHMM)和逻辑回归(Logical Regression)模型作为对比．模型的识别效果通常用准确率(accuracy，Acc)、灵敏度(sensitivity，Sen)和特异性(specificity，Spe)3个评价指标进行表示[18]．公式如下：

(17)

(18)

(19)

其中Tp为正例被判为正例(true positive)，Fn为正例被判为负例(false negative)，Tn为负例被判为负例(true negative)，Fp为负例被判为正例(false positive)．正例为清醒样本，负例为疲劳样本．利用上述公式对GM-HMM、DHMM和Logical Regression模型的驾驶疲劳识别结果进行分析，对比结果如表2所示．

可见，GM-HMM模型的3个评价指标均高于另外两种模型．建立3个模型的接受者操作特征(receiver operating characteristic，ROC)曲线如图14所示．其中横坐标Fpr为ROC曲线中的假阳性率(false positive rate，Fpr)，纵坐标Tpr为真阳性率(true positive rate，Tpr)，ROC曲线下的面积(AUC)大小代表模型识别准确率．ROC曲线越靠近左上，即曲线下的面积越大，表示其性能越好．结合表2，从图14中可以看出本文所提出的GM-HMM相比DHMM和Logical Regression模型具有更好的检测效果．

表2 模型的准确率、灵敏度和特异性Tab.2 Accuracy,sensitivity and specificity of models

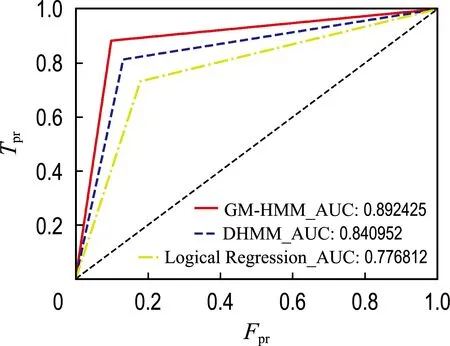
图14 不同模型的ROC曲线Fig.14 ROC curves of different models

4 结 语

针对车载驾驶疲劳检测系统研究中的驾驶人疲劳辨识准确率低的问题，本文首先选取了能有效反映驾驶疲劳变化的EEG信号作为观测序列数据；其次，结合驾驶疲劳的动态生成特性，采用高斯混合模型拟合观测序列，提出了一种基于GM-HMM的驾驶疲劳检测方法；最后，为了进一步分析所建模型的优势，分别设置了基于DHMM和基于Logical Regression模型的驾驶疲劳检测方法作为对比．对比测试结果表明，本文所提出的基于GM-HMM的驾驶疲劳检测方法在准确率、灵敏度和特异性方面具有较大优势，此研究成果可为相关车载驾驶疲劳检测系统研发提供参考．

鉴于实验场地、人员招募以及模型中驾驶疲劳分级等的限制问题，未来将针对更多复杂路况、更多参试者和多级疲劳状态类型来优化所建模型，进一步提升模型的检测准确率．