惯导系统结构拓扑优化方法研究

杨晨曦，余盛强，闫红松,袁大义，王永振

(北京自动化控制设备研究所，北京 100074)

0 引言

惯导系统是运载火箭等飞行器和其他载体中广泛应用的精密测量仪器，其工作精度和可靠性直接影响着载体的控制精度和可靠性[1]。新一代飞行器要求飞行速度更快、射程更远，在提升动力性能的同时，结构减重是目前一项亟待解决的关键技术难题。惯导系统作为飞行器的核心导航控制电子设备，在精度指标要求不断提升的同时，还要求其具有小型化、轻质化、力学环境适应性强等特点。同时飞行器动力性能的提升使惯导系统面临比以往更加严酷的振动、冲击及噪声环境条件，而传统的结构设计模式主要基于现有的设计规范及设计师的个人经验，在设计基本完成后进行力学仿真校核，结构减重主要依据个人经验，缺少科学的计算数据支撑，这就造成了减重设计不合理及多轮的设计反复，影响了设计质量和研制周期。如何使惯导系统结构在满足力学环境适应性要求的同时，又能实现大幅度轻量化，是惯导系统结构设计的一项重要研究内容。除采用轻质化的高强度材料外，基于结构拓扑优化技术的正向创新设计是目前最有效的一种技术手段。

近年来，国内已经开始把拓扑优化技术应用在惯导系统结构设计中。如李雄魁等对运载火箭惯组基座进行了拓扑优化设计，确定了一种轻质化、高刚度的悬臂惯组基座结构形式[2]；刘仲宇等对航空遥感惯性稳定平台内框架进行了拓扑优化设计，减小了平台内框架的总质量，提高了平台的动态性能[3]；王平等对无人机惯导减振系统支架进行了拓扑优化设计，在减重的基础上提升了一阶模态频率[4]；徐江涛等对光纤陀螺结构进行了结构优化设计，在满足频率和光纤环体积的条件下,减小了结构的质量,轻量化效果明显[5]；陈兴好等对惯性台体结构进行了拓扑优化设计，在满足一阶频率要求的前提下减重效果明显[6]。上述工作均以质量或一阶模态频率作为目标函数，以一阶模态频率或质量作为约束条件，主要对结构振动这一典型工况进行优化，而没有考虑结构在承受其他力学载荷(例如大气压力)等多种工况下的优化。此外，在边界处理上也大多对安装面直接进行理想刚性约束,这种假设与真实情况存在差异，一般来说拓扑构型也并不理想。王立平等将子模型技术引入装配体结构的拓扑优化中，对边界条件进行了精确提取[7]，但这种方法仅适用于静力学工况，并不适用于惯导系统结构件所受的模态工况。

本文基于拓扑优化理论，提出了考虑多工况组合和等效边界处理方法的惯导系统典型结构拓扑优化方法，梳理了适用于惯导系统结构的拓扑优化流程。并以某惯导系统盖板、惯性台体和外壳体组成的系统为实例进行拓扑优化设计，优化结果在满足刚度和频率约束的前提下，实现了结构质量大幅减小，拓扑优化构型清晰，取得了良好的优化效果。

1 结构拓扑优化理论与方法

结构优化是对结构设计的优化，根据设计变量的范围大体分为三个层次：拓扑优化、形状优化和尺寸优化，分别对应产品的概念设计、基本设计和详细设计阶段。拓扑优化主要是在规定的设计区域内，在给定的载荷和边界条件下，通过改变结构的拓扑来满足应力、频率和位移等约束条件；形状优化是在给定结构和拓扑的基础上，对其边界形状进行优化；尺寸优化是在给定结构的类型、拓扑和形状的基础上，对构件尺寸进行优化。与尺寸优化和形状优化相比，拓扑优化不仅待优化参数更多，对优化目标的影响更大，取得的效果也更好，是当今结构优化设计研究领域的热点[8-9]。

结构拓扑优化方法主要有均匀化法、变密度法、独立连续映射法(Independent Continuous Mapping，ICM)、渐进结构优化法(Evolutionary Struc-tural Optimization，ESO)和水平集法等[10]。均匀化方法寻优效率低，独立连续映射法程序实现较难，渐进结构优化法通用性差，水平集法过程过于复杂，而变密度法设计变量少、通用性强、寻优效率高、程序易于实现、灵敏度计算较易，是目前工程上应用最为广泛的方法[11-12]。

变密度法的基本思想是在优化中引入一种材料，其密度在[0 1]区间内连续可变，并假设结构材料的其他物理参数也与材料密度值有一定对应关系。优化过程中，设计变量为结构材料在[0 1]间连续可变的密度，当密度取值为0～1之间的中间值时，通过选用合适的惩罚函数因子对设计变量进行惩罚，使中间密度能够向两端靠近，从而使结构的优化模型能够尽可能地只存在0和1两种相对密度单元，得到实体和孔洞分明的优化结果[13-14]。

变密度法模型为

ρ=Xeρ0

(1)

式中：Xe为设计区域里的每个单元的相对密度；ρ0为拓扑优化的设计变量。当Xe为1时，则表示该单元材料为实，需要保留或添加此单元；当Xe为0时，则表示该单元材料为空，应该删除此单元(孔洞)；当Xe在0～l之间时，根据密度设定来判断对该单元进行保留或者删除。

2 惯导系统结构拓扑优化方法

2.1 惯导结构拓扑优化数学模型

惯导系统一般由陀螺、加速度计、光源盒、导航计算机、直流电源、IF转换电路、惯性台体、系统主壳体、盖板、减振器和连接器等零部件组成。其中，惯性台体、盖板和外壳体是结构设计的主要内容，也是结构轻量化设计的重点关注对象。

盖板结构主要承受压力载荷，在满足刚度要求的条件下，结构频率也是影响系统动力学性能的重要因素。因此，在进行盖板类结构优化时，需要综合考虑压力载荷工况和模态工况，将结构最大变形和结构一阶频率作为设计约束，考虑工艺性，对盖板施加制造约束。当盖板左右对称时，施加对称约束；当盖板安装有电路板等组件时，还要考虑安装位置接触。

惯性台体由于安装在壳体内部，不承受压力载荷。在进行惯性台体拓扑优化时，主要考虑模态工况。

壳体和盖板类似，主要承受压力载荷，在进行壳体拓扑优化时，要考虑模态工况和压力载荷工况。考虑到安装工艺性，安装支耳区域不进行优化。

惯导系统在工作中主要经受振动、冲击、过载等动力学环境，以及高空环境压力载荷、密封检漏过程压力载荷、重力载荷等多种组合工况，因此，拓扑优化模型中需要综合考虑多种工况组合。经过大量分析研究与验证，惯导系统结构拓扑优化的典型优化模型可以描述为以最大化刚度，暨柔度最小为目标的优化模型，结构体积分数、结构频率、结构最大变形及具体制造约束等为约束条件的数学问题[15]

(2)

式中:设计变量X={x1,x2,x3,…,xi}T为经有限元离散后的单元相对密度;Ω为优化设计变量的集合;C为结构的柔度;K、U和F分别为结构的整体刚度、位移和外荷载矩阵;V(xi)和V*分别为结构的实际体积关于变量xi的函数和整个优化问题的约束体积分数值;G(X)和H(X)为一阶固有频率和最大变形函数,G*为设计频率，H*为结构允许的最大变形；xmin和xmax分别为设计变量的上下限值;i为单元数量。

2.2 等效边界处理方法

除目标函数与约束条件具体设置外，载荷工况与边界条件是影响拓扑优化结果的关键因素。传统拓扑优化方法中，如果仅导入单独零件，并直接对其安装面施加固定约束，在运算中会把固定面视为刚度无限大的刚体面，这种假设与实际情况有明显差异，导致拓扑优化结果并不是真实工况下的最优解；而如果将待优化零件置于装配体中进行优化计算，则会因结构复杂、接触非线性等问题导致迭代缓慢，甚至难以收敛。为了尽可能准确地描述结构优化区域的边界条件，考虑装配连接刚度影响，本文在对盖板和惯性台体进行单独拓扑优化时，提出了一种等效边界处理方法：把外壳体上与盖板和惯性台体接触的面向下切割分离，并对切割后的外壳体下表面固定约束。由于外壳体安装支耳区域不进行优化，故不进行等效边界处理。

2.3 惯导系统结构拓扑优化流程

惯导系统结构比较紧凑,尺寸、质量及安装接口限制较多，需要预先考虑惯性器件、导航计算机和直流电源等零部件的空间摆放位置，形成方案的初始设计。在初始设计的基础上，传统设计主要通过挖减重孔、槽等实现轻量化设计，而这种轻量化设计方式主要基于工程师的设计经验，布局不尽合理，并不是轻量化的最优解。本文提出的惯导系统结构拓扑优化方法是在初始设计方案的基础上进行的，其主要流程如下：

首先分析了结构模型,以确定优化区域即优化模型中的设计区域，并根据可允许设计的空间限制，充分利用可以填充结构的空间,使设计区域在布局限制下最大化；其次，根据各零部件安装接口位置，局部切割作为非设计区域；包含设计区域与非设计区域的模型建好后，进行有限元建模，并根据各结构件所受工况，施加载荷及边界条件；进行优化模型定义，提交求解器计算；对拓扑优化结果进行模型重构，并对该结构进行具体工况下的仿真分析，若各性能指标不满足设计要求，再在拓扑优化后的模型上进行局部针对性的尺寸优化，最终使各性能指标均满足设计要求。图1所示为适用于惯导系统结构的拓扑优化设计流程[16]。

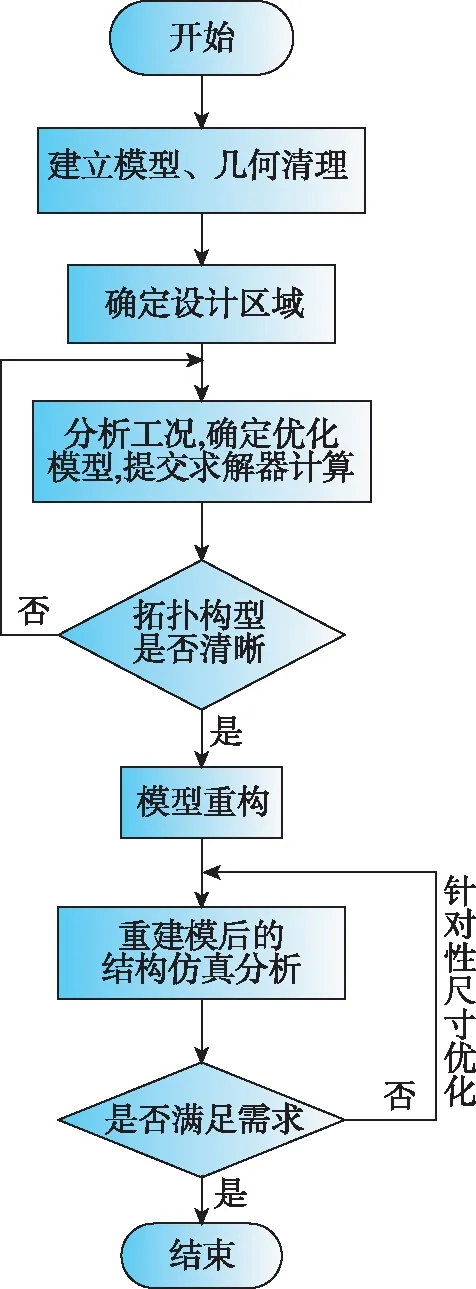
图1 拓扑优化流程Fig.1 Process of topology optimization

3 应用实例

3.1 模型分析

本文在研究的基础上，以某惯导系统的三种典型结构件为实例，进行了拓扑优化分析。

某惯导系统惯性台体组件主要由3个加速度计、3个陀螺、1个连接器和1个光源盒等构成。盖板上装有1块电路板，通过一周法兰面与外壳体进行螺栓连接。外壳体结构较为复杂，安装有2块电路板和4个连接器，通过4个安装支耳进行固定。

预先考虑惯性台体、盖板、电路板和连接器等零部件的空间摆放位置和整体安装接口位置，形成方案的初始设计。为了提高仿真计算效率，在导入有限元分析软件分析之前，对模型进行了适当的简化处理：

1)陀螺仪、加速度计、连接器和光源盒等按照实体建模，以等厚度的平板代替电路板。

2)螺钉预紧力对被连接构件的刚度不产生明显影响，且两接触面不产生相对滑移，故将螺纹孔用构件材料填充，仅在螺钉头压紧的圆形区域内将两构件的接触面黏合在一起，圆形区域的直径各取螺纹直径d与螺钉头直径dk,min的1.5倍。

简化后的惯导系统初始结构如图2所示。

(a)盖板

3.2 传统设计模型

基于工程经验，在初始设计的基础上进行传统设计，方案模型如图3所示。

3.3 惯导系统优化

3.3.1 模型等效边界处理

通过等效边界处理方式，分别对初始设计的盖板和惯性台体模型进行处理，壳体结构不进行等效边界处理，如图4所示。

3.3.2 网格划分

网格密度为3mm，各组件节点数和单元数如表1所示。

表1 各组件节点数和单元数

3.3.3 材料属性

惯导系统结构件材料为2A12铝合金。零部件采用等效密度,即零部件质量除以简化后体积,各组件材料的弹性模量和泊松比采用工程经验参数。

图4 等效边界处理后的惯导系统结构Fig.4 INS structural parts after equivalent boundary treatment

材料属性如表2所示。

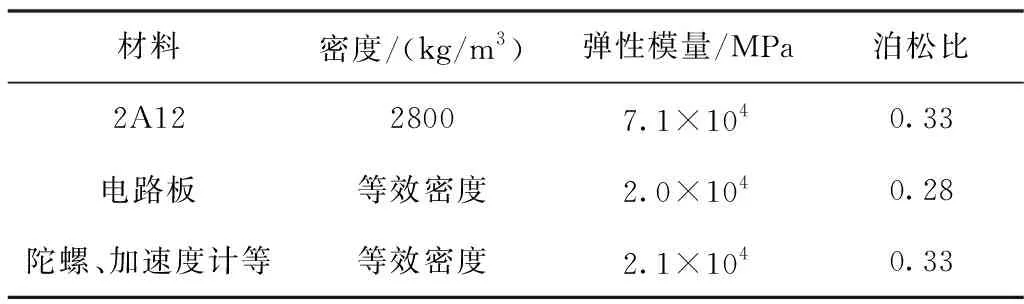
表2 材料属性

3.3.4 优化参数设置

求解器计算，通过修改密度阈值，切除密度值小于0.5的材料。根据拓扑优化结果，各结构均得到了清晰的拓扑构型，可作为模型重构的参考。考虑到密封性，盖板和主壳体上镂空部分需要加一层蒙皮。惯性台体拓扑构型呈现出桁架结构形式，需要根据模型重构后的仿真情况对局部进行尺寸优化，优化参数如表3所示。

表3 优化参数设置

3.3.5 重建模后仿真分析

将拓扑优化计算得到的结果导出STL文件，进入NX建模界面重建模。拓扑构型与重建模后的模型如图5所示。重建模后的模型以上述分析方式分别进行模态分析，最终优化后的各结构仿真结果如图6所示。

图5 各结构的拓扑优化结果Fig.5 Topology optimization results of each structure

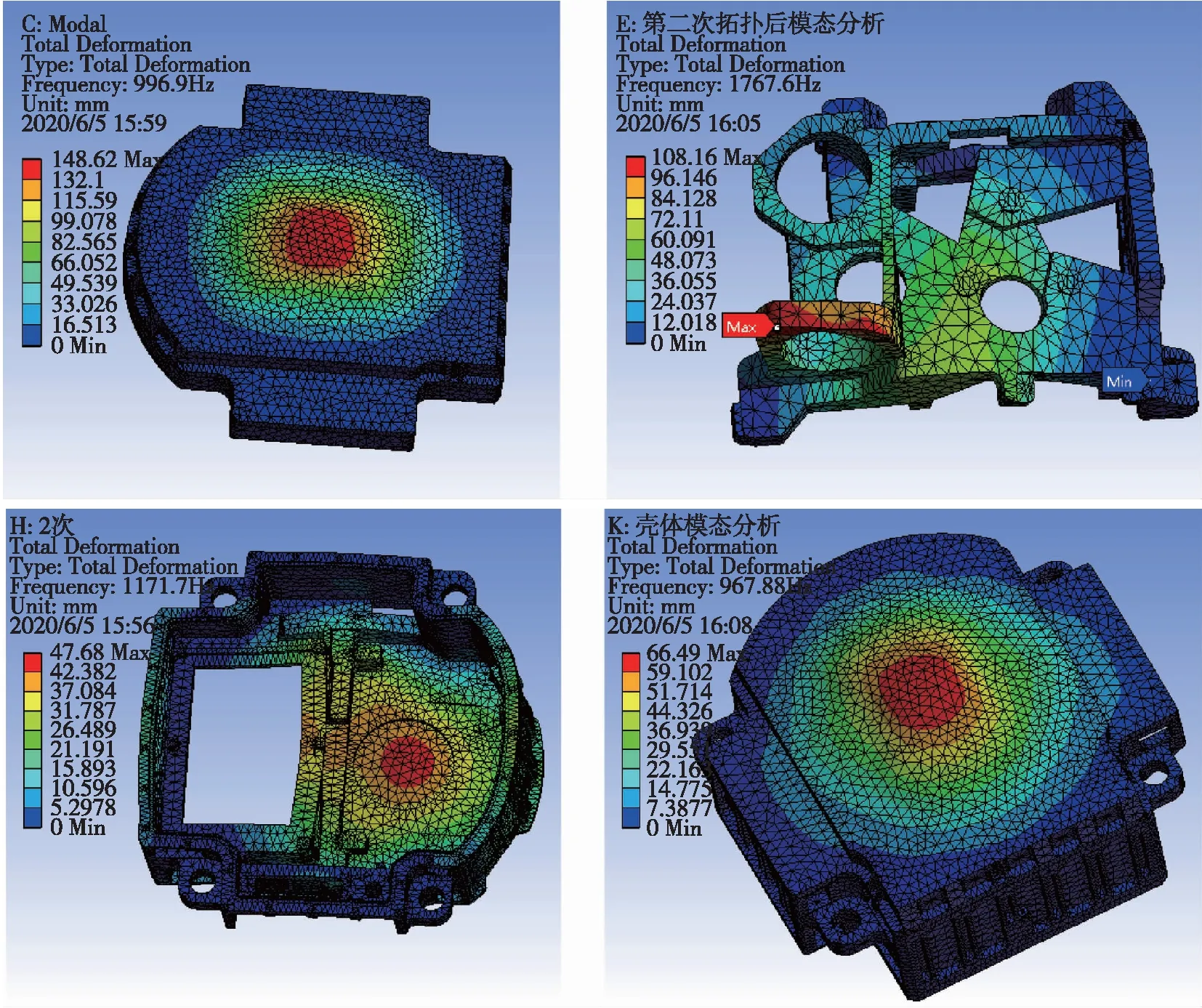
图6 优化后的结构仿真分析结果Fig.6 The simulated analysis results of each optimized structure

3.4 传统设计模型模态分析

对传统设计进行模态分析，结果如表4所示，各结构一阶模态振型如图7所示。通过等效边界建模进行分析的误差均不超过10%，在可接受范围内。

图7 各结构一阶模态振型Fig.7 First mode formation of each structure

表4 传统设计模态分析结果

3.5 结果对比

传统结构设计和采用拓扑优化设计后的一阶模态、质量对比如表5所示。由结果可以看出，通过拓扑优化，惯导系统结构件在模态提升的情况下，质量大幅度减小，达到了轻量化的目的。

表5 传统结构设计和采用拓扑优化设计后的一阶模态、质量对比

4 结论

针对传统惯导系统结构件拓扑优化中，没有考虑除模态工况外，由密封等工艺条件而产生的低气压压力载荷等工况，以及装配体拓扑优化中，复杂程度和迭代速度与安装面刚度的准确性存在矛盾，本文提出了考虑多工况组合和等效边界处理方法的惯导系统典型结构拓扑优化方法，建立了适用于惯导系统结构的拓扑优化流程。并以某惯导系统结构件为实例，分别对其盖板、惯性台体和外壳体进行优化后，其各自和组合成的装配体较传统经验设计结构模态均有所提升，质量明显减小。本文提出的研究方法同样适用于其他惯导系统结构件的拓扑优化设计。