基于三维原子磁强计的核磁共振陀螺仪实验优化

李连花，徐正一，彭欣欣，周尹敏，裘栩炀，魏梦梦，周 敏，徐信业

(华东师范大学精密光谱科学与技术国家重点实验室，上海 200062)

0 引言

陀螺仪是用来测量物体相对于惯性空间旋转角度或角速度的传感器，是惯性导航系统(Inertial Navigation System，INS)的核心部件之一。与全球定位系统(Global Position System，GPS)相比，惯性导航系统可以在许多特殊环境下工作，如深海和洞穴[1]。核磁共振陀螺仪(Nuclear Magnetic Reson-ance Gyroscope, NMRG)利用原子自旋进动来测量角速度，具有精度高、体积小、功耗低、对加速度不敏感等优点[2-5]。核磁共振陀螺仪也是未来高精度、芯片级陀螺仪的研究热点[6-7]。

1938年，伊西多·拉比成功地进行了第一次核磁共振实验，随后他于1944年获得了诺贝尔物理学奖[8]。1952年，通用电气公司提出了核磁共振陀螺仪的概念，并于1955年获得了名为《角运动测量仪》的专利[9]。从那时起，其他公司和研究机构也开启了自己的核磁共振陀螺仪研究。1979年，美国Litton公司和Singer-Kearfott公司分别研制出光泵浦核磁共振陀螺仪的原理样机。前者陀螺仪的零偏稳定性为0.1(°)/h、角度随机游走为0.01(°)/h1/2，后者的性能指标分别为0.05(°)/h和0.015(°)/h1/2[10-11]。为解决弱信号检测和磁场稳定这一问题，美国斯坦福大学和英国萨赛克斯大学转向研究低温超导核磁共振陀螺仪[2]。然而，由于环形激光陀螺仪和光纤陀螺仪的快速发展，许多研究机构逐渐放弃了对核磁共振陀螺仪的研究。直到2005年，美国国防部高级研究计划局(Defense Advanced Research Projects Agency，DARPA)开始在定位、导航和授时(Positioning, Navigation and Timing, PNT)方面开展micro-PNT项目，核磁共振陀螺仪被列为重点资助项目。在DARPA的资助下，诺格公司(Nor-throp Grumman)在体积为10cm3的物理封装中研制出了角度随机游走为0.001(°)/h1/2、零偏稳定性为0.01(°)/h的核磁共振陀螺仪[12]。2016年，北京自动化控制设备研究所成功研制了体积为50cm3的样机，其角度随机游走为0.2(°)/h1/2、零偏稳定性为1(°)/h[13]。此外，美国加州大学欧文分校和美国国家标准与技术研究院(National Institute of Standards and Technology，NIST)也对核磁共振陀螺仪的关键技术进行了研究[14-15]。

本文展示了一种基于三维原子磁强计的核磁共振陀螺仪。通过检测进动的原子核磁矩来获得参考系的角速度，因此将三维原子磁强计集成到核磁共振陀螺仪中是构建小型化核磁共振陀螺仪的一种有效途径。磁场的波动会影响核磁共振陀螺仪的角速度测量，所以优化三维原子磁强计的静磁场调制度、激励磁场幅度等重要参数可更好地补偿剩余磁场。在三维磁场闭环锁定后，获得了角度随机游走为0.038(°)/h1/2、零偏稳定性为0.94(°)/h的核磁共振陀螺仪。

1 基本原理介绍

核磁共振陀螺仪的基本原理主要包括光泵浦超极化原子的制备和高灵敏原子磁强计探测，工作原子一般选用碱金属原子和惰性气体原子[16]。首先通过光泵浦将碱金属原子极化，经过碱金属原子与惰性气体原子的自旋交换碰撞，从而实现惰性气体原子的超极化。惰性气体原子的旋磁比小，由碱金属原子构建的磁强计通过探测惰性气体原子核磁矩来更灵敏地测量角速度。

核磁共振陀螺仪的工作原理如图1所示。原子的核自旋指向在未发生极化时各不相同，为使核自旋获得宏观磁矩，首先在z轴方向施加泵浦光和静磁场B0z(如图1(a)所示)，使碱金属原子的价电子发生极化，之后碱金属原子与惰性气体原子发生碰撞，使电子自旋极化转移到了惰性气体的原子核，这样核自旋就获得了沿z轴方向的宏观磁矩M。单个的核磁矩以拉莫尔(Larmor)进动频率围绕z轴进动，它们进动的相位互不相同，故合磁矩M在x-y平面净分量为0。为了实现核磁共振陀螺仪测量载体装置角速度的功能，磁矩M需要在x-y平面内有分量，从而在x-y平面内进动。因此，可以沿x轴方向施加一个激励磁场，使得惰性气体原子核自旋进动与外加激励磁场发生共振，所以激励磁场的频率应约等于惰性气体原子核磁矩进动的拉莫尔频率。如图1(b)所示，所加激励磁场为B1cos(ωat)，其中激励磁场大小为B1，激励磁场频率满足ωa≈γB0z，γ为惰性气体原子旋磁比。在施加激励磁场后，核自旋磁矩与外加激励磁场发生核磁共振，使得惰性气体原子核自旋磁矩进动的相位一致，则磁矩M在x-y平面内有一个分量磁矩Mxy，会以惰性气体原子的拉莫尔频率绕着z轴方向进动。磁矩M绕着静磁场B0的进动可以用式(1)描述

(1)

其中，静磁场B0的x、y和z轴方向分量分别为B0x、B0y和B0z，本文沿z轴方向施加静磁场，即这里只考虑z轴方向分量B0z。

如图1(c)所示，如果陀螺仪所处载体装置的参考系绕着z轴方向开始旋转，那么观测频率ωobs就变为

ωobs=ωL-ωR=γB0z-ωR

(2)

其中，ωL为惰性气体原子的拉莫尔进动频率(满足ωL=γB0z)；ωR为载体装置参考系的角速度。将磁矩M的进动方向定义为参考系的正向旋转方向，假定旋磁比和外加静磁场大小已知，通过测量观测频率ωobs，根据式(2)可知参考系的角速度ωR，这是核磁共振陀螺仪测量载体装置角速度的基本原理。

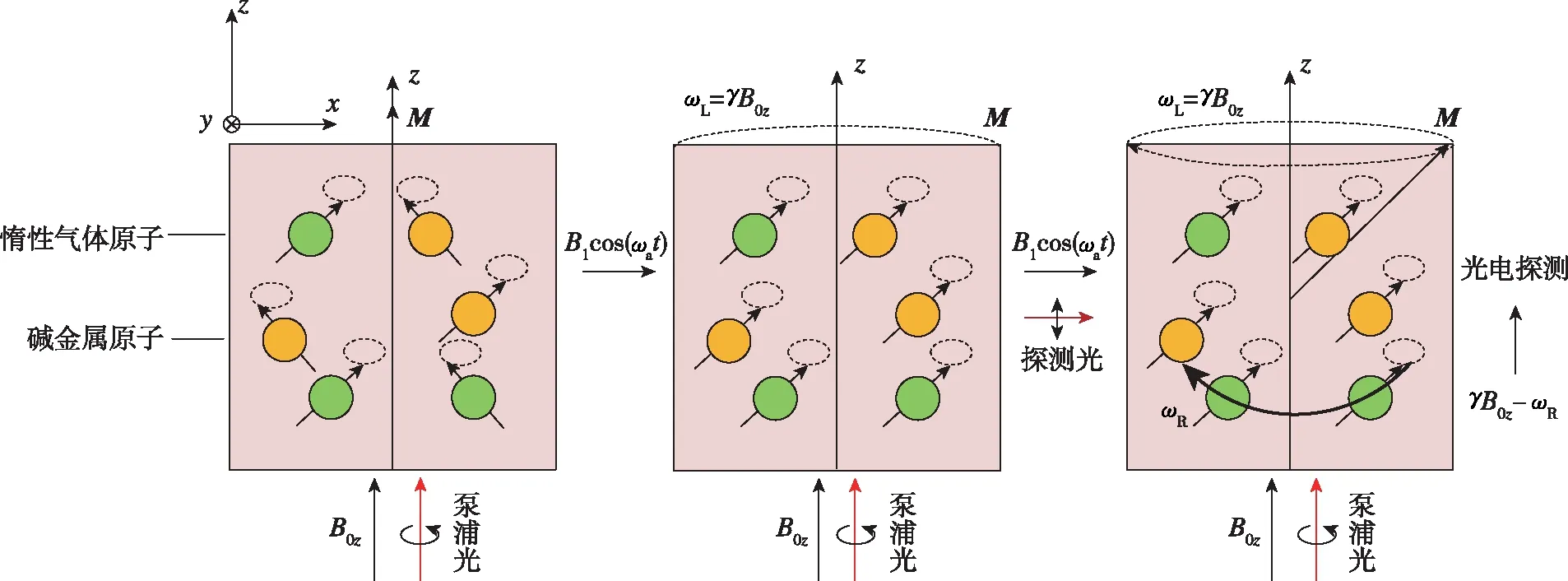
(a)原子极化 (b)施加激励磁场 (c)探测角速率ωR图1 核磁共振陀螺仪的原理图Fig.1 Schematic diagram of NMRG

本文展示的核磁共振陀螺仪是基于133Cs-129Xe/131Xe原子所研制的，为了构建基于133Cs原子的非线性旋光探测的三维原子磁强计，需要对纵向磁场进行高频调制，以达到消除低频闪烁噪声和提高信噪比的目的。施加调制后的纵向磁场Bz满足Bz=B0z+Bccos(ωct)，其中Bc为调制幅度，ωc为调制频率，并且调制频率等于Cs原子的拉莫尔进动频率，即ωc=γCsB0z。Cs原子的动力学过程可以用布洛赫方程来描述，横向磁化强度可以通过求解布洛赫方程来获得[17-18]，布洛赫方程的解可以表示如下

J1-p(k)]sin(pωct)-By[J1+p(k)+

J1-p(k)]cos(pωct)}

J1-p(k)]cos(pωct)+By[J1+p(k)-

J1-p(k)]sin(pωct)}

(3)

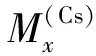
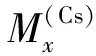
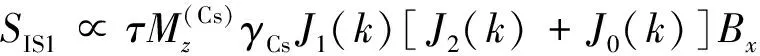
(4)

定义x和y方向上信号与磁场之间的标度因子分别为kx和ky。则它们可以表示如下

kx1∝J1(k)[J2(k)+J0(k)]
ky1∝J1(k)[J2(k)-J0(k)]
kx2∝J1(k)[J3(k)-J1(k)]
ky2∝J1(k)[J3(k)+J1(k)]

(5)

其中，下标1和2表示p=1或p=2。为了使磁场测量更为灵敏，应使式(5)中的复合贝塞尔函数最大化。标度因子kx和ky的绝对值与调制度k的关系如图2所示。

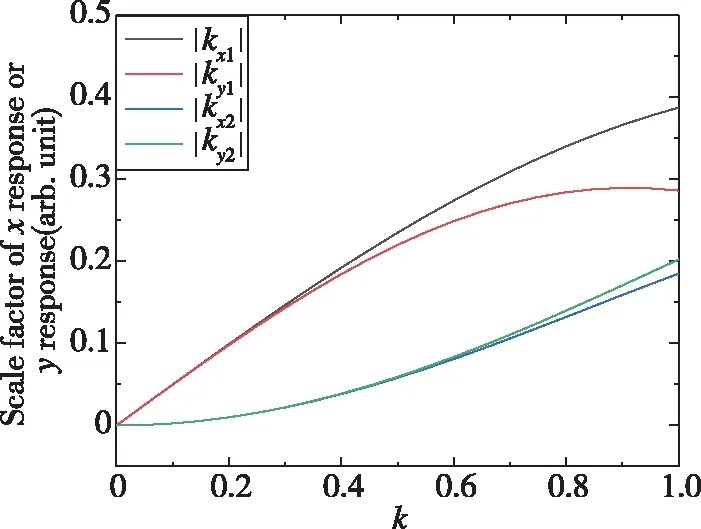
图2 kx1、ky1、kx2和ky2的绝对值与调制度k关系的仿真结果Fig.2 The simulation result of the relationship curve between the absolute value of kx1, ky1, kx2 and ky2 and the modulation degree k

由图2可知，当调制度k小于1时(实验中采用电流源输出电流通过线圈产生Bz，且对电流实施幅度调制,目前使用的电流源仅限于单个方向的输出，因此k不能超过1)，有|kx1|>|kx2|和|ky1|>|ky2|，因此实验中选择ωc作为参考频率而不是2ωc来解调探测到的信号。当调制度k小于1时，标度因子kx和ky随k的增大而增大。当调制度一定时，同相信号SIS和正交信号SQS在一定范围内分别与磁场Bx和By成正比，因此可以通过测量同相信号SIS和正交信号SQS获知Bx和By的大小和方向。

Xe原子的进动和自旋弛豫也满足布洛赫方程。Xe原子磁矩M与磁场B之间的相互作用关系可以表示为[17]

(6)

其中，Mx、My和Mz分别为Xe在x、y、z方向上的磁化分量;M0为Xe原子在热平衡状态下的磁矩;T1和T2分别为纵向自旋弛豫时间和横向自旋弛豫时间，用来描述弛豫过程。

如果沿x轴施加激励磁场B1cos(ωat)，以频率ωa为参考频率解调My，得到色散型信号和吸收型信号为

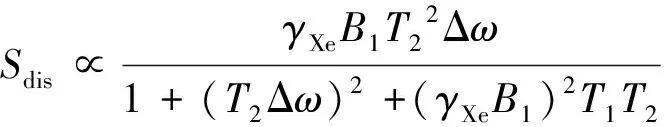
(7)

其中，Δω=γXeBz-ωa-ωR，ωa=γXeB0z。当核磁共振陀螺仪的磁场锁定后,即Bz=B0z，则Δω=-ωR，此时可通过色散信号Sdis测角速度ωR；如果核磁共振陀螺仪保持静止，则Δω=γXe(Bz-B0z)，则可通过色散信号Sdis测Bz在B0z附近的波动。

对于色散型信号，零点Δω=0处的斜率表示为

(8)

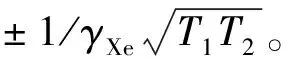
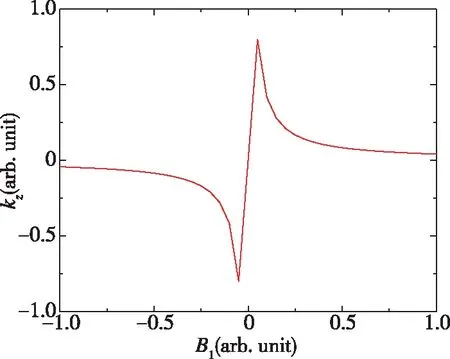
图3 色散信号斜率kz与激励磁场幅度B1关系的仿真结果Fig.3 The simulation result of the relationship between the slope kz of the dispersion signal and the amplitude of the oscillating magnetic field B1

2 实验结果与分析

实验装置如图4所示，气室为边长1.5cm的立方体，其中包含133Cs、10Torr(1Torr=133.322Pa)的129Xe、10Torr的131Xe和200Torr的N2，并通过一对无磁加热片将其加热到约107℃。气室被放置在一个五层圆柱形磁屏蔽筒中，其屏蔽因子为106。左旋圆偏振泵浦光使Cs原子泵浦后极化，然后通过Cs原子与Xe原子之间的自旋交换碰撞，从而使Xe原子超极化。泵浦光束光功率为120mW，其由沿z轴施加的分布式布拉格反射(Distributed Bragg Reflector, DBR)激光器产生，该激光被调谐到Cs原子的D1谐振频率处。另外，N2用于消除自发辐射并减少极化原子与气室壁的碰撞。三维磁场线圈用于产生磁场并补偿剩余磁场。除了静磁场(B0z=2.5μT)外，还沿z轴施加了调制磁场Bccos(ωct)，并且调制频率等于Cs原子的拉莫尔进动频率(ωc=8750Hz)。此外,沿x轴施加了一个激励磁场，其频率等于129Xe原子的拉莫尔进动频率(ωa=29.65Hz)。另一个DBR激光器被调谐到Cs原子的D2谐振频率处，沿着y轴发射了250μW的线偏振探测光进入蒸气池。探测光的偏振面由于原子的自旋极化而被调制，并由平衡光电探测器探测，该平衡光电探测器由3个锁相放大器(Lock-in Amplifier, LIA)解调。以Bz磁场为参考的LIA-x的同相输出和LIA-y的正交输出分别用于解调获取Bx和By磁场大小。用x方向激励磁场频率ωa作为参考解调得到的LIA-z正交输出可用于测量Bz磁场。

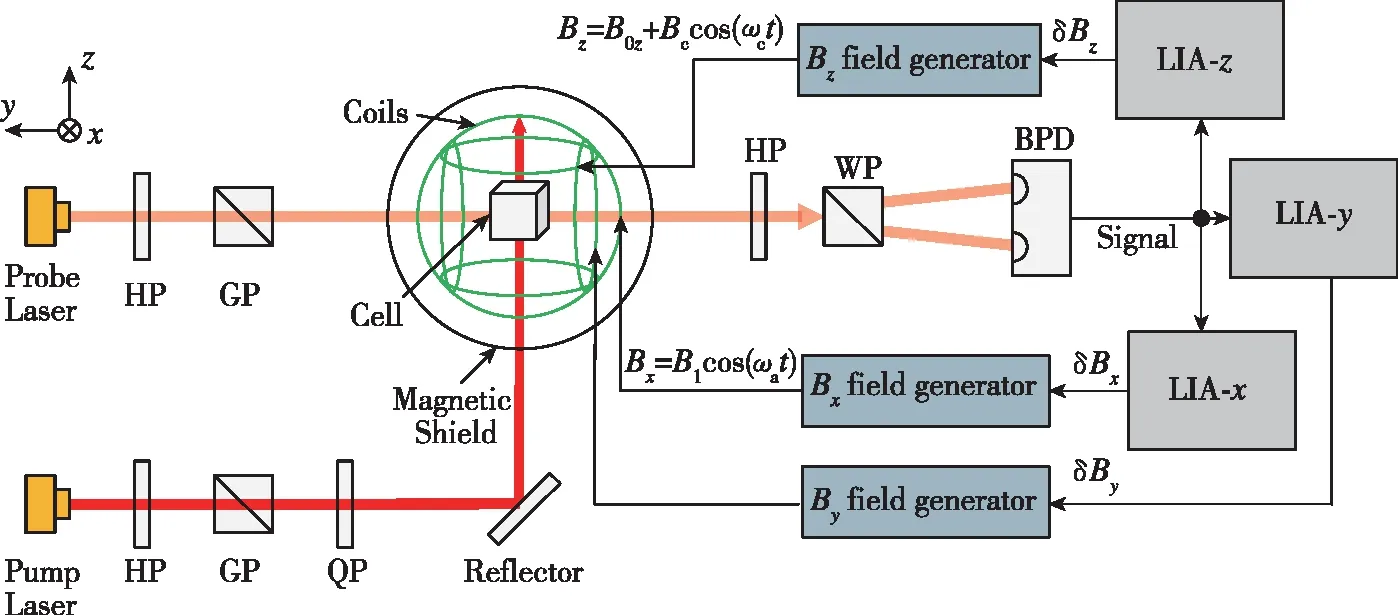
HP：半波片；GP：格兰棱镜；QP：四分之一波片；WP：沃拉斯顿棱镜；BPD：平衡光电探测器；LIA：锁相放大器图4 核磁共振陀螺仪实验装置Fig.4 Experimental setup of NMRG

核磁共振陀螺仪通过测量Xe原子自旋进动的拉莫尔频率来测量角速度，拉莫尔频率与沿z轴方向的纵向磁场有关。另外，如果横向磁场太大，也会影响拉莫尔频率。因此，构造一个三维原子磁强计来测量和补偿磁场十分有必要。为了使三维原子磁强计足够灵敏，实验上需要优化静磁场调制度k和激励磁场幅度B1等参数，从而使磁强计的标度因子足够大。

为了获得灵敏的三维原子磁强计，首先要优化调制度k。尽管x和y轴相位相差π/2，但是为了保持它们的独立性，使用2个锁相放大器对ωc处的信号进行解调，分别获得x和y轴上的磁场，它们的相位略有不同。设置静磁场B0z=2.5μT，调制磁场幅度Bc分别为0.42μT、0.84μT、1.25μT、1.67μT和2.09μT，相应的调制度k分别为16.8%、33.6%、50.0%、66.8%和83.6%。通过扫描改变Bx和By的大小，可以得到解调信号和磁场之间的关系，如图5所示。

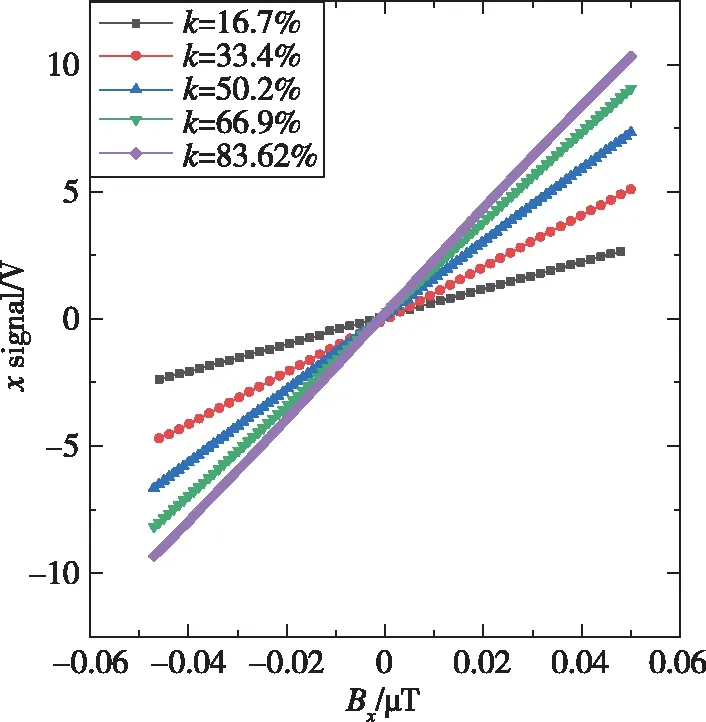
(a) x轴

由图5可以看出，随着调制度的增加，x、y轴磁强计信号的标度因子kx和ky也随之增加。当调制度k为83.6%时，磁强计信号的标度因子达到最大，这也与图2中的仿真结果一致，说明实验上该条件下的x、y轴磁强计性能最优。

实验上为了使z轴磁强计信号的标度因子足够大(标度因子为色散信号零点处的斜率)，需要对激励磁场B1的振幅进行优化。为探究B1对z轴磁强计信号的影响，设定B1的幅度在1.6～8.6nTpp范围内变化。扫描z轴磁场得到的z轴磁强计信号如图6所示，其中频率是由z轴磁强计信号和Xe原子的旋磁比转换得到的。利用式(7)对信号进行拟合，可以得到B0z=2.5μT时，B1对z轴磁强计信号标度因子kz的影响，如图7所示。当B1=2.6nTpp时，标度因子kz最大，也就是说实验中该条件下z轴磁强计性能更好。

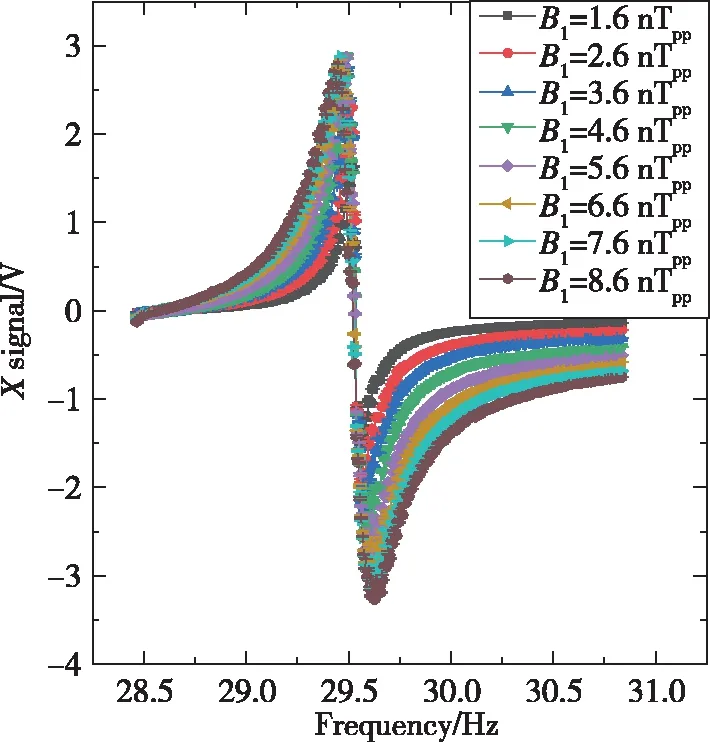
(a) X信号是z轴锁相放大器的X通道信号

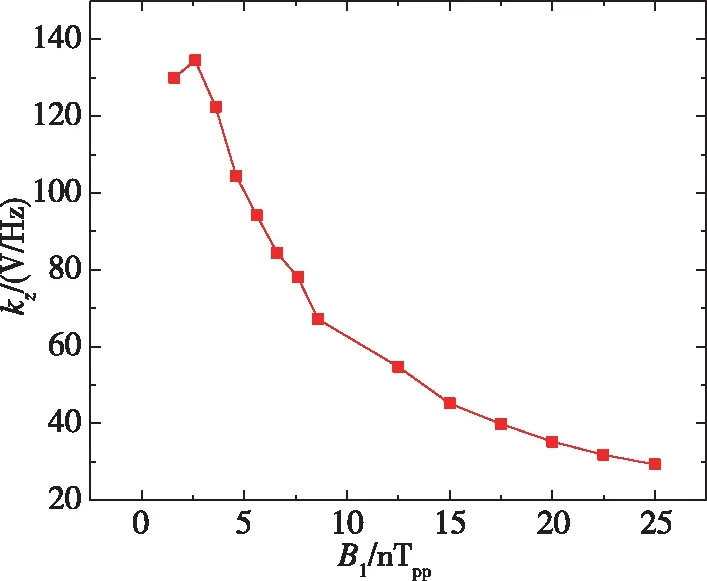
图7 z轴磁强计信号斜率kz与激励磁场幅度B1关系的实验结果Fig.7 The experimental result of the relationship between the slope kz of the magnetic field signal along the z axis and the amplitude of the oscillating magnetic field B1

通过优化实验参数，研制了一个可用于测量三维磁场的灵敏度更高的三维原子磁强计。基于图4所示的闭环反馈实验装置，将三维磁场锁定，以补偿剩余磁场。锁定前后三维原子磁强计的输出结果对比如图8所示，实现了磁场锁定后6000s内Bx、By、Bz起伏分别不大于143pT、147pT和28pT的锁定效果，而锁定前Bx、By、Bz的6000s内起伏范围分别约为351pT、587pT和79pT。

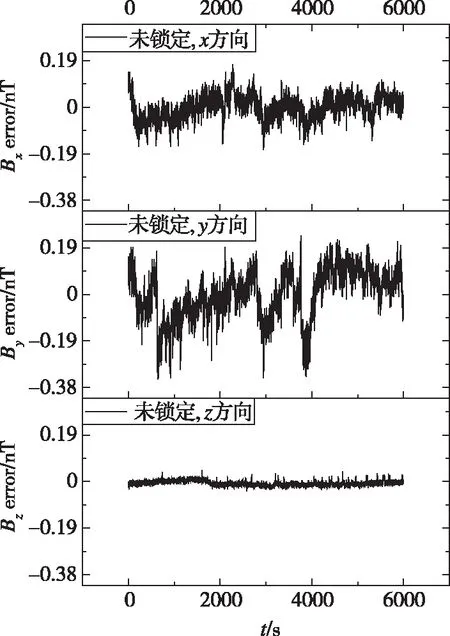
(a)未锁定

为了测试核磁共振陀螺仪的性能，保持核磁共振陀螺仪静止，测量其在6000s内的输出角速度波动，其Allan偏差分析如图9所示。通过拟合Allan偏差曲线[19]，得到核磁共振陀螺仪的角度随机游走和零偏稳定性分别为0.038(°)/h1/2和0.94(°)/h。

图9 核磁共振陀螺仪角速度起伏Allan偏差的实验和拟合结果Fig.9 Experimental and fitting results of Allan deviation for angular rate fluctuation of the NMRG

3 结论

综上所述，本文展示了一种基于三维原子磁强计的核磁共振陀螺仪。通过优化静磁场调制度k和激励磁场幅度B1，找到了更优的工作条件，得到了更灵敏的三维原子磁强计，可以更好地测量和补偿三维磁场。基于核磁共振陀螺仪测量角速度的原理，这些优化进一步提高了核磁共振陀螺仪的性能。最后得到了角度随机游走和零偏稳定性分别为0.038(°)/h1/2和0.94(°)/h的核磁共振陀螺仪。未来可通过优化气室温度和气室内原子的配比，进一步提高核磁共振陀螺仪的性能。