一种MEMS陀螺仪零偏建模与估计方法

王国栋，孙丽艳，王振凯，杨 亮

(北京航天控制仪器研究所，北京 100094)

0 引言

随着微机电系统(Micro-Electro-Mechanical System，MEMS)惯性器件精度的不断提升，微纳卫星、机器人、无人机和影视特拍等军、民用领域越来越多地采用MEMS惯性器件作为姿态测量和导航的重要部件产品[1-2]。高精度的MEMS陀螺仪作为角速率测量的惯性器件，是实现精确姿态测量和导航的核心关键[3-4]。MEMS陀螺仪的精度取决于仪表的设计、加工、标定和误差补偿等多个环节[5-7]。其中，设计和加工是保证MEMS陀螺仪精度的前端环节，标定和补偿是保证和提升MEMS陀螺仪精度的后端环节。对于MEMS陀螺仪标定和补偿的前提是其各项误差参数具有稳定的性质或变化规律，这样才能通过标定予以去除和补偿。陀螺仪的零偏具有一定的漂移性，很难通过常规的全温标定方法[8-9]予以完全补偿。这是由于MEMS陀螺仪的零偏取决于自身结构以及封装应力、材料缺陷、电路偏移等多种因素，所有这些因素都与温度有关。随着温度的变化，各种影响因素的特性会发生变化，导致陀螺仪的零偏产生相应的漂移。当陀螺仪工作时，其零偏漂移主要由自身发热所引起[10]，以及在整个器件工作过程中其他变化因素变化而引起的漂移。

为了消除温度对陀螺仪零偏的影响[11]，往往会通过测量不同温度点下的陀螺仪零偏，建立零偏关于温度的数学模型，实现陀螺仪的零偏误差补偿[12]。然而，这种模型一般是针对陀螺仪整个工作温度范围而建立的，在大的温度变化范围内能够实现零偏的误差建模和补偿。由于建模的温度范围跨度大、取样点有限，必然存在模型误差，因此常规的温度建模方法建立的模型仅能够近似地给出某温度下的陀螺仪零偏值。将零偏估计值从陀螺仪的输出中予以扣除，一定程度上实现了MEMS陀螺仪的零偏误差补偿。通过这种方式建立的零偏温度模型，对于大的温度范围内的零偏变化是有效的，对于温度小幅度变化范围内的零偏漂移，难以有效描述。此外，随着时间的推移，惯性仪表的结构应力等材料特性会发生变化，使得前期建立的温度模型精度下降。由于受到系统拆装和成本等因素的制约，往往难以重复开展温度建模标定。在实际应用中，陀螺仪在连续工作过程中，其温度会随着环境温度的变化在温度平衡点附近小范围内做上下波动，这种小幅的波动也会导致陀螺仪的零偏变化和测量精度下降。温度是影响MEMS陀螺仪零偏变化的主要因素，因此可以通过建立零偏关于温度的关系模型，进一步实现陀螺仪的零偏估计和补偿。

针对MEMS陀螺仪在使用过程中温度小幅波动引起的零偏漂移问题，提出了一种零偏建模和估计方法，实现了MEMS陀螺仪的零偏有效估计，为陀螺仪的误差补偿和精度保持提供了技术基础。

1 MEMS陀螺仪零偏建模

建立系统的数学模型包括两种方式，一是分析方法，二是系统辨识的方法。分析方法是利用系统工作的内在物理客观规律以及结构参数，推导出系统的数学模型。然而由于系统的复杂性和某些结构参数的不可测性，导致很难基于分析方法建立系统的数学模型。系统辨识的方法是基于系统的输入输出测量值等先验知识，假定系统的数学模型，选择合适的估计方法估计模型的参数，并通过试验加以验证。

MEMS陀螺仪由于结构的复杂性，很难采用分析方法建立零偏关于温度小幅度变化的模型，因此采用系统辨识的方法建立其模型。MEMS陀螺仪零偏随着温度的变化是一个连续动态平衡过程，这种连续过程可以采用微分方程的形式予以描述[13]；对于数字量输出系统，一般采用差分方程[14]的形式予以描述。如图1所示，2020年5月26日在实验室内测得某型MEMS IMU陀螺仪的零偏和温度变化曲线，1h取一个零偏均值，连续通电测试24h内的零偏数据。从图1中可以看出，由于环境温度的变化，陀螺仪的温度是一个连续动态平衡过程，温度在整个测试过程中有小幅变化。整个过程中，随着温度的上升和下降，陀螺仪零偏经历先下降后波动，再上升之后下降的过程。采用传统的代数方程多项式，难以描述零偏跟温度之间的关系。因此，选用差分方程进行零偏和温度的数学关系描述。

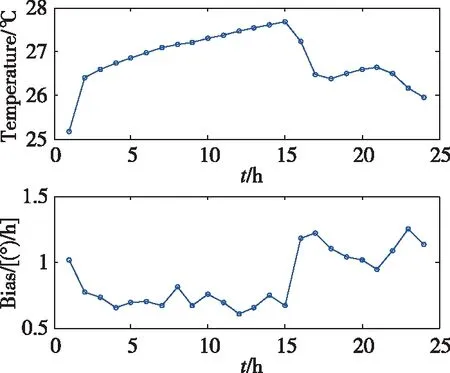
图1 陀螺仪零偏、温度变化曲线Fig.1 Bias and temperature of the gyroscope

以温度T为输入变量，零偏Y为输出变量，建立系统的差分方程

Yn+a1Yn-1+a2Yn-2+…+akYn-k=

b0Tn+b1Tn-1+b2Tn-2+…+bmTn-m

(1)

式(1)中，k为差分方程的阶次，Yn-k，…，Yn-1，Yn为从n-k时刻到n时刻的陀螺仪零偏；Tn-m，…，Tn-1，Tn为从n-m时刻到n时刻的陀螺仪温度；a1，…，ak，b0，…，bm为方程的系数，k≥m，共有k+m+1个待求系数。差分方程阶次k可以根据系统的建模误差和样本点波动情况进行选取。样本点的取样间隔越小，零偏波动越剧烈，选择的差分方程阶次越高；反之，则方程的阶次越低。基于陀螺仪的试验数据分析，可以选择较为合适的差分方程阶次。

由式(1)可得

Yn=-a1Yn-1-a2Yn-2-…-akYn-k+

b0Tn+b1Tn-1+b2Tn-2+…+amTn-m

(2)

从式(2)可以看出，陀螺仪零偏Yn不仅与当前时刻的温度Tn有关，还跟以前时刻的Yn-1，…，Yn-k和Tn-1，…，Tn-m有关。如果已知(n-k) ～(n-1)时刻的陀螺仪零偏和(n-m)～(n-1)时刻的陀螺仪温度，就可以根据式(2)递推得到n时刻以及后续时刻的陀螺仪零偏，从而实现陀螺仪的零偏估计。

2 模型参数的辨识流程

在建立MEMS陀螺仪零偏和温度的误差模型之后，根据式(2)可以开展模型的参数识别。具体实施步骤如下：

1)数据采集。根据设定的取样间隔Δt，获取一段时间内的MEMS陀螺仪零偏和温度值，零偏和温度值均取时间间隔Δt内的数据均值。

2)基于式(2)，得到一系列的差分方程组，方程的个数(N-n)>(k+m+1)，如式(3)所示

(3)

将式(3)用矩阵表示，可以简化为

Y=Z·C

(4)

式中，Y是式(3)左侧零偏输出构成的列向量矩阵；Z是式(3)右侧陀螺仪零偏和温度构成的矩阵；C是式(3)右侧差分方程的系数构成的列向量矩阵。

3)基于最小二乘法，可以得到系数向量C

C=(ZTZ)-1ZTY

(5)

根据式(5)，可以得到系统的建模误差

Δ=norm(Y-ZC)

(6)

4)零偏-温度构成的系统稳定性分析。由式(1)可得系统的Z变换

(7)

通过求解方程1+a1Z-1+…+an-1Z-k=0的所有特征根z1,z2,…,zk，并判断所有特征根是否位于Z平面的单位圆内，即特征根的模值|zi|<1，以确定系统是否稳定。如果有一个特征根不在单位圆内，则系统不稳定，需要重新选择模型的阶次k和m值，重复步骤2)～4)，直到找到合适的系统参数为止。建模及模型参数的辨识流程如图2所示。

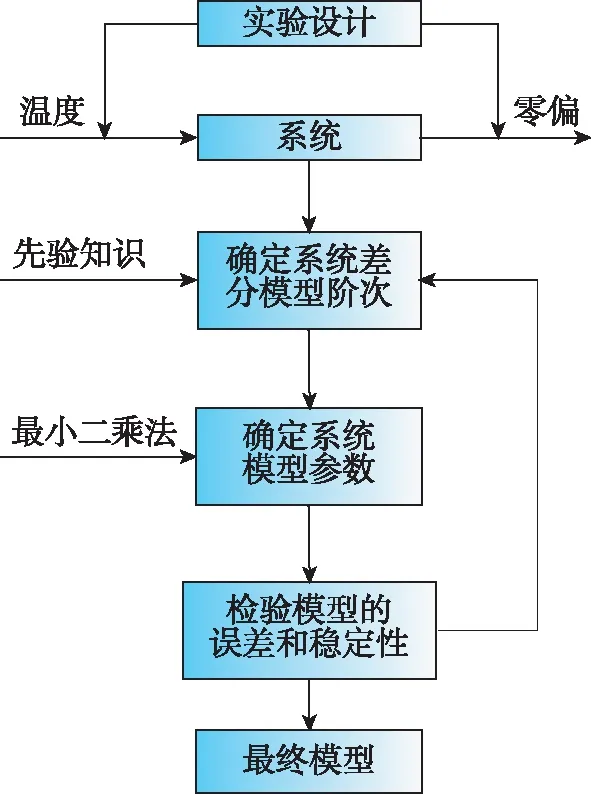
图2 建模及参数辨识流程Fig.2 Flow chart of modeling and parameter identification

3 试验验证与分析

为了验证提出方法的有效性，设计了验证试验。在实验室内，将某型高精度短时自主导航用MEMS IMU置于大理石平板上，给MEMS IMU连续通电。如图3所示，MEMS IMU东北天放置，监测MEMS IMU东向陀螺仪的输出即零偏值，测试时长为72h。该MEMS IMU试验前期经过了三轴温箱转台全温范围的标定和温度补偿。MEMS IMU内置的MEMS陀螺仪为四质量块对称结构陀螺仪，通过检测电容的变化实现对外界角速率的敏感。

图3 测试环境Fig.3 Testing environment

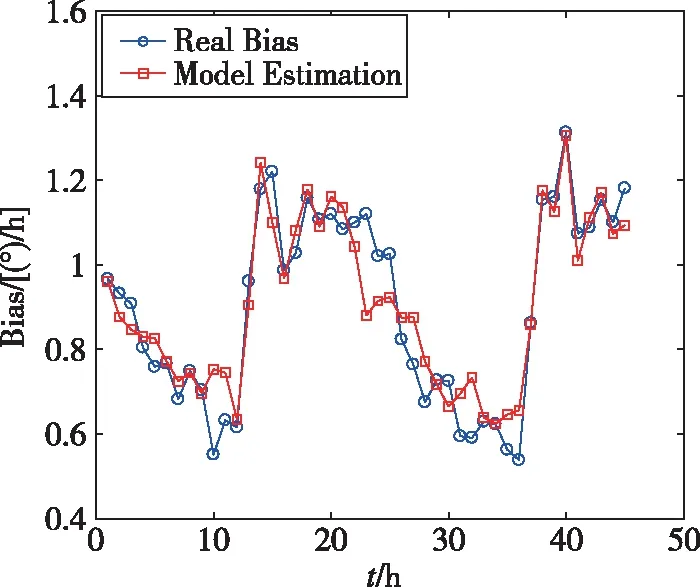
在5月26日—28日连续通电测试，得到72h的样本数据。以1h为一个取样间隔，1h内的温度和零偏均值作为一个样本数据对，共获得72对样本数据。前24对样本数据如图1所示，用于零偏建模和模型参数识别；后48对样本点用于模型的性能验证，如图4所示。由图4可知，由于实验室环境温度的变化，陀螺仪的温度在25℃～28℃之间波动，是一个动态热平衡的过程。连续2d的温度变化规律趋于一致。陀螺仪的零偏随着温度的变化呈现出一定的规律，当温度上升时下降，当温度下降时上升。

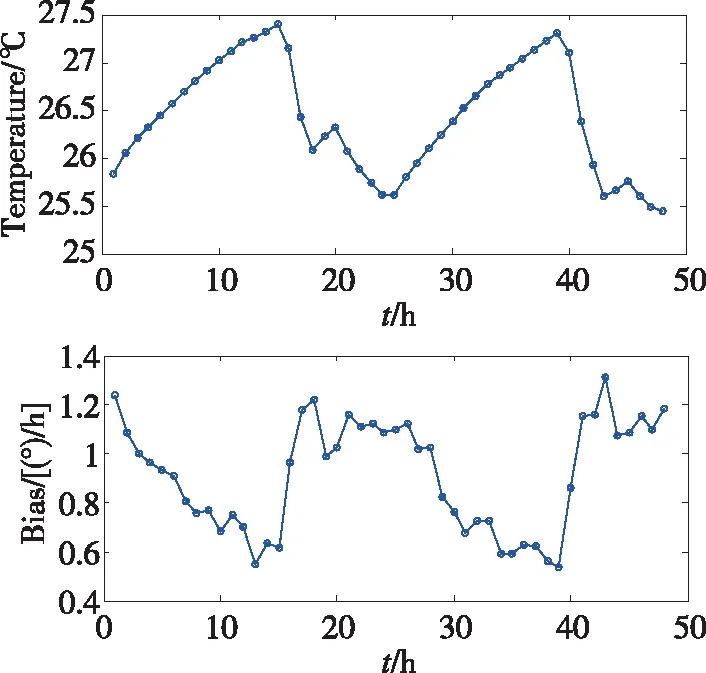
图4 模型性能验证的取样数据Fig.4 Sampling data used to verify the model

利用提出的方法建立系统的差分方程，经过建模和参数识别过程，通过比较1～4阶的建模误差，选择模型的阶次为3(k=3,m=3)，差分方程的系数如表1所示。

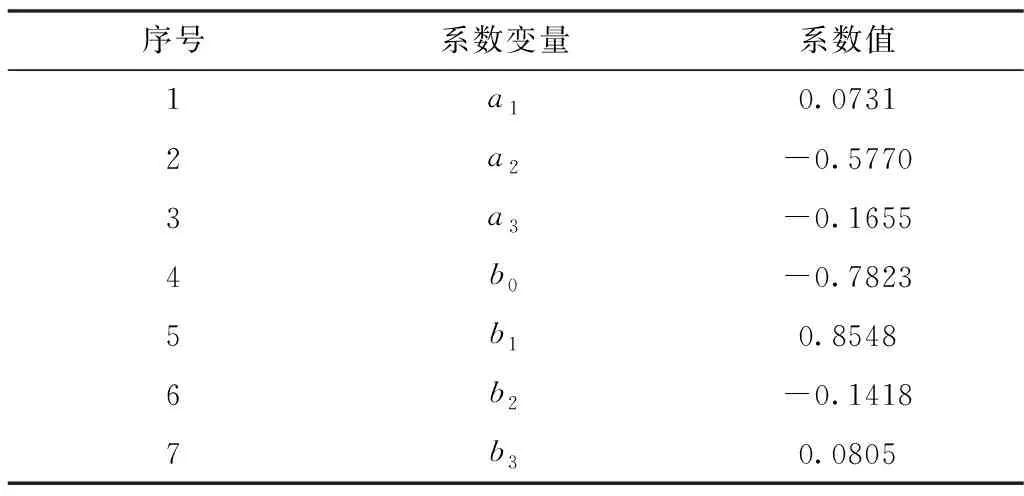
表1 三阶差分模型系数

(a)单步估计

(a)二阶多项式模型估计

表2 模型估计的误差

4 结论

1)通过分析MEMS IMU陀螺仪在稳态工作过程中零偏随温度的变化规律，建立了零偏关于温度的差分方程模型，并给出了差分模型的参数识别过程；

2)通过试验验证，给出了某型MEMS IMU陀螺仪的零偏三阶差分模型，试验结果表明：零偏温度差分模型能够实现陀螺仪零偏的高精度估计，模型多步估计的误差是三阶多项式模型估计误差的65.37%；

3)多步估计是基于含有误差的估计值递推得到的，由于不断引入误差，估计的误差相比单步估计会有所增加；

4)基于零偏的历史数据，实现对零偏漂移的精确单步估计和多步估计，可以有效地估计和补偿陀螺仪零偏的漂移，满足多种场景下的应用需求。