基于Kinect三维重建的地下井室可视化方法研究

余兆凯，彭晓峰，邱昌杰

(中国电建集团贵州电力设计研究院有限公司,贵阳 550003)

0 引言

随着地下空间信息化程度的提高，传统二维图像和视频信息的表达方式已经无法满足地下井室及管道的可视化要求。传统的地下井室测量多使用人工测绘、2D成像和24目井下机器人测量等方案[1-3]。但人工测绘存在危险性高、人力成本高、准确度难以保证等缺点；而普通2D图像由于丢失了深度信息，故无法精确测量三维尺度信息，且由于拍摄区域有限导致无法获取井下全貌；24目井下机器人结构复杂、体积庞大、适用性较差，而且设备使用前需要在特定的标定室进行标定，标定繁琐且成本较高[4-6]。总体而言，现有的地下井室测量手段存在三维信息缺失、效率低下以及成本较高等缺点。RGB-D深度相机可在任意光照条件下获取被测目标的深度图像数据，且可较好地应用于地下空间环境，对于地下空间的三维重建具有重要意义[7-10]。针对上述应用中存在的问题及行业需求，本文基于RGB-D深度相机对地下井室进行视觉三维重建，以实现其内部环境状况的三维可视化，并在三维实测点云模型的基础上，对地下空间的缺陷状况进行定量分析，为地下空间的病害探测与维护提供了技术支持。

深度相机种类繁多，其中Microsoft公司推出的Kinect深度相机具有代表性。基于深度相机的三维可视化研究众多，也出现了一些具有代表性的工作。P.Henry等通过在室内移动Kinect传感器设备采集得到数据，结合深度和彩色信息进行三维重建，并在后端中加入闭环检测进行优化，但重建结果质量不佳，且实时性较差，精度有待提高[11]。Microsoft公司针对Kinect发布的KinectFusion三维模型重建算法[12]，利用Kinect深度传感器自由转动获取室内场景深度数据，通过与点云域截断符号距离函数(Truncated Signed Distance Function，TSDF)模型匹配的方式进行位姿估计，并将所有数据融合到模型中实现三维场景的重构。该项目实现了实时的三维重建，但是缺少彩色纹理信息，且需要利用图像处理器(Graphics Processing Unit，GPU)进行加速计算。由于KinectFusion算法使用固定体积的网格模型表示重建的三维场景，因此只能对固定大小的场景目标进行三维重建。TSDF模型将整个待重建的空间划分为相同大小的网格，当重建场景较大时，或者网格的空间分辨率较高时，会占用大量的显存空间[13]。另外，该算法缺少回环检测和回环优化，当相机移动距离较大时，不可避免地存在误差累积，易造成重建场景的漂移。T.Whelan等在KinectFusion算法的基础上,提出了Kintinuous算法。该算法结合了迭代最近点(Iterative Closest Point，ICP)算法和直接法，用于提升位姿估计精度。使用动态的网格模型进行场景数据的融合，对相机量测范围内任意大小的场景都可进行三维重建，融合了回环检测和回环优化，对重建结果进行优化，对累积误差进行控制。T.Whelan等提出了ElasticFusion算法[14]，采用了不同于KinectFusion方案的surfel面元模型进行数据融合。使用OpenGL对点云进行更新、融合、显示和投影，通过ICP算法计算相机间的位姿信息，并基于构建的变形图进行优化。采用融合重定位算法，当相机跟丢时，可重新计算相机的位姿[15]。该方案适合对房间大小的场景进行三维重建，但在较大场景下适用性较差。

1 Kinect深度数据预处理及误差修正方法

1.1 基于多项式曲面拟合的深度测量误差修正方法

针对Kinect深度相机在不同方向上的测距误差表现，提出了一种基于多项式曲面拟合的深度测量误差修正方法。Kinect的三角测量原理可通过图1所示的示意图进行表示，根据三角形相似可得

(1)

其中，Zo为参考平面深度值;f为红外相机的焦距；b为基线长度；d为视差。由式(1)得到被测目标的深度为

(2)

图1 Kinect三角测量原理Fig.1 Kinect triangulation principle

若令Δd为视差误差，则深度测量的误差ΔZk可以表示如下

(3)

视差误差由系统误差所决定，系统误差是固定的，因此，视差误差也是不变的。由式(3)可知，深度测量误差与测量距离成正比。通过上述Kinect三角测量的误差模型，可以得到每一个像素点的真实深度值F(u,v)关于Kinect测量距离Zk的多项式曲面模型，即

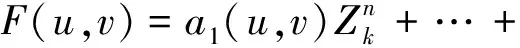
(4)

式中，a1(u,v),…，an(u,v)代表多项式系数；b(u,v)表示常数项。

1.2 Kinect深度图像预处理

联合双边滤波器是一种基于双边滤波器的改进算法，可用于低分辨率图像升采样，从而填补图像的信息缺失[16-17]。双边滤波算法中由一幅图像计算得到所有的权值，而在联合双边滤波算法中，通过再引入一幅具有丰富信息的图像计算权值，可得到更优的权值。RGB-D相机可以同时获取目标深度图像和RGB图像，其中RGB彩色图像中包含了场景的完整信息，可以用来补全深度图像的缺失部分。因此，本文在联合双边滤波算法的基础上，实现对深度图像的快速滤波去噪。

联合双边滤波权值函数表示如下

w(i,j,x,y)=wg(i,j,x,y)×wr(i,j,x,y)

(5)

其中，(i,j)和(x,y)表示选取的2个像素点坐标，且彩色图像灰度域权值wr和深度图像空间域权值wg计算公式如下

(6)

(7)

式中，g(i,j)和g(x,y)分别代表在像素点(i,j)和(x,y)处，将彩色图像转化为灰度图像后得到的灰度值。

2 稠密三维点云重建及可视化方法

2.1 结合SIFT匹配和RANSAC算法的点云初始位姿估计

深度相机可以快速获取场景目标的深度及彩色信息，从而得到彩色点云数据。但是，由于深度相机视角范围有限、场景目标的尺寸较大以及障碍物的遮挡等原因，一次从一个角度的扫描方法只能获取被测目标的部分数据。因此，需要从不同角度进行多次数据采集，以获取场景目标的全局点云数据。不同视角下获得点云数据的坐标系是不一致的，需要通过点云配准的方式将其统一到同一坐标系下。

尺度不变特征转换(Scale-Invariant Feature Transform，SIFT)算法可以对图像中的区域特征进行检测和描述，其原理是在建立的不同尺度空间中检测关键点，并计算其方向。SIFT主要检测信息明显的关键点，对于遮挡目标的检测效果也较为明显。且SIFT特征的信息量较大，适合在海量数据库中快速准确匹配[18]。在获取到图像的SIFT特征点后，对相邻两帧图像进行特征匹配，以获取两帧图像之间的位姿变换关系。传统的随机抽样一致性(Random Sample Consensus，RANSAC)算法利用随机选取的特征点进行匹配，忽略了特征点的差异性，易造成图像的错误匹配。改进的RACSAC算法基于迭代的思想，先对迭代过程中的随机采样结果进行筛选操作，将存在明显错误的匹配点对剔除。其原理如下：

1)假设相邻两帧图像提取到的ORB(Oriented FAST and Rotated BRIEF)特征点集合为

P={pi|pi∈P,i=1,2,…，m}
Q={qi|qi∈Q,i=1,2,…，m}

(8)

查找P中特征点pi在Q中最近邻和次近邻的2个特征点。若与最近邻和次近邻的欧式距离之比小于设定的阈值，则认为pi与最近邻ORB特征点是一对匹配点。

2)利用双向匹配机制，即找到P中特征点在Q中对应的特征点，同样找到Q中特征点在P中对应的点。若二者一一对应匹配，则认为该匹配是正确的，将匹配不正确的结果进行剔除，以达到筛选的目的。

3)通过设定最小匹配距离阈值，将筛选剩余的匹配结果中大于最小匹配距离一定倍数的部分剔除。经过上述步骤得到匹配质量较高的匹配点对。

2.2 结合邻域特征的ICP点云精确配准方法

在利用SIFT算法对图像数据进行匹配后，获取了图像数据帧之间的初始位姿信息。在特征点匹配的基础上，进一步利用基于邻域特征的ICP算法实现三维点云间的精确位姿估计，从而实现点云精确配准，其算法流程如图2所示。

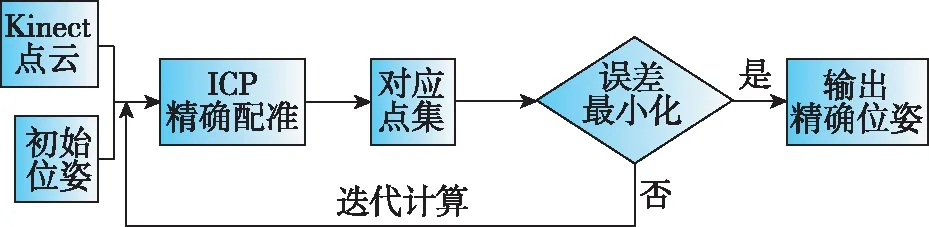
图2 ICP点云精确配准流程Fig.2 Point cloud precise registration process with ICP algorithm

首先建立邻域特征，其原理如下：

(9)

其中，n为采样点的邻近点数量。点云的方差σN和均值μN计算如下

(10)

式中，N为点云的采样点数量，将采样点邻域曲率处于μN±ασN之外的点作为选取特征点。其中α是用于调整特征点数目的调整因子。

2)确定对应点：假设P和Q为两片相邻的点云，若要找到点云P中特征点pi在点云Q中的对应点，可通过选取Q中最近邻近的3个点作三角形。

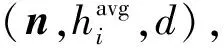
在邻域特征建立完成后，基于建立的邻域特征,使用ICP算法进行相邻两帧点云间的精确位姿估计。假设P和P′是已经匹配好的点对

P={p1,…,pn}
P′={p′1,…,p′n}

(11)

即找到一个欧式变换R和t，使得

∀i,pi=Rp′i+t

(12)

3 实验分析

3.1 Kinect深度相机误差修正

实验对Kinect深度传感器的测距结果与激光测距结果进行分析，得到了Kinect在测距视场范围内的多组深度测量误差及其变化情况。利用获取的深度误差数据，构建真实深度值关于测量距离的多项式曲面模型，基于最小二乘法原理对得到的测量误差数据进行拟合，得到测量深度关于深度误差的拟合公式，其拟合结果如图3所示。

图3 Kinect测距误差距离曲线拟合Fig.3 Kinect ranging error distance curve fitting

图3中的深度误差结果经曲面函数模型拟合后得到如下拟合公式

y=4E-10x3-3E-6x2+0.01x

(13)

式中，y为误差修正值;x为距离值。若Kinect v2.0深度值为d，测得修正深度误差为

d′=d-(4E-10x3-3E-6x2+0.01x)

(14)

通过多项式曲面拟合的误差修正方程对深度误差进行修正，得到修正后的误差分布结果，如图4所示。

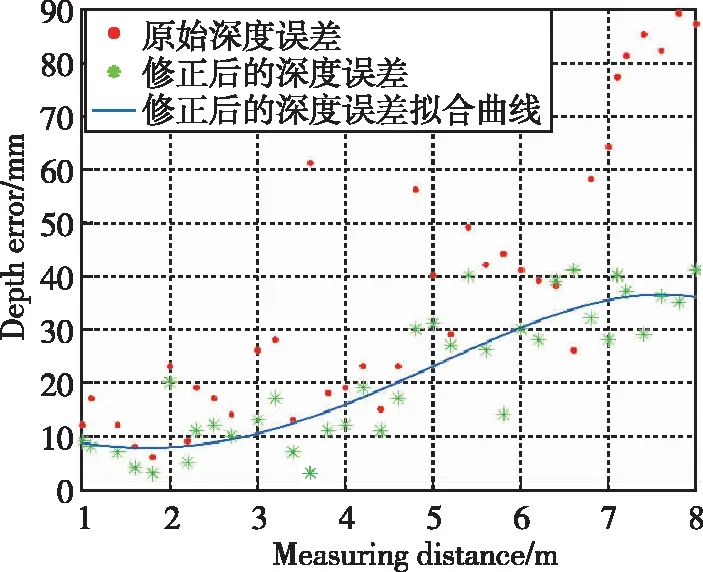
图4 深度误差修正结果Fig.4 Depth error correction result

由图4的实验结果可以看出，原始深度误差随着测量距离的增加出现急速增长的趋势，而经过误差补偿修正后的深度误差随距离增加的变化较为平缓。且当Kinect深度传感器在0.5～4.5m的测距范围内时，其深度测量误差小于2cm；在4.5～7m的测量范围内时，其深度测量误差也可以保持在4.5cm以内。实验结果表明，本文提出的误差修正方法可以较好地修正Kinect深度测量数据的误差，有效提升其测距精度。

3.2 地下井室稠密三维点云重建

地下井室空间狭小且纹理单一，常规的激光扫描仪在其中难以作业。针对地下井室应用场景的需求，本文采用基于飞行时间(Time of Flight，ToF)测距原理的Kinect v2.0深度传感器作为图像采集设备。如图5所示，首先通过机械传动装置将Kinect v2.0深度相机置于地下井室中，从上、中、下3个视角旋转获取了3个不同方位的深度及彩色数据。实验设置转动设备选择次数默认值为16次，每次旋转角度20°，从井室的3个层次对其进行数据采集。采集时保证深度相机量测距离至少为1m，确保获得的数据质量更佳。设置设备采集范围为0.6～7.5m，保证获取数据的有效性。由于Kinect v2.0深度传感器的视场角为水平70°，垂直60°，其在垂直和水平方向的覆盖范围有限。因此，在实际测量中将Kinect v2.0深度传感器分别向上、向下倾斜一定的角度，进行多次扫描，从而增加相机的采集覆盖范围，确保经过一周旋转后采集的图像数据间存在较多重叠。

图5 Kinect地下井室数据采集Fig.5 Underground wells data acquisition by Kinect

3.2.1 SIFT特征点匹配结果

实验通过SIFT特征点算法对获取的图像数据进行匹配，获得初始的位姿估计信息，为后续的ICP点云精确配准提供较优的计算初值，进一步提升点云图像的配准精度。图6(a)所示为地下井室图像的SIFT特征点原始匹配效果，其中存在较多的误匹配，不利于图像帧间的初始位姿估计。为提升初始位姿的估计精度，利用改进的RANSAC算法对特征匹配结果进行处理，剔除其中的误匹配结果，如图6(b)所示。实验选取了其中一组数据进行统计，得到表1所示的匹配结果。实验结果表明：经过改进的RANSAC算法处理后的特征点匹配率明显提升，正确匹配率可达95.24%，有效剔除了其中的错误匹配点对。

(a)原始匹配结果

表1 SIFT特征点匹配结果统计

3.2.2 局部及全局点云配准结果

在SIFT特征匹配提供的位姿估计初始值上，利用结合邻域特征的ICP算法可实现对局部帧间点云和全局点云的精确配准。帧间点云配准结果如图7所示，可以看到，经过ICP算法精确配准后的两帧点云之间实现了很好的拼接融合，局部配准的细节也有不错的表现。在进行两帧点云的精配准后，仅实现了局部的点云配准，并未将全局的点云进行融合。进一步通过基于邻域特征的ICP精配准算法对多视角的点云进行融合，得到全局一致的点云重建配准结果，如图8所示。实验统计了两帧点云以及全局点云的精确配准结果，并同经典ICP算法[19]进行了对比分析，两种算法配准结果如表2所示。实验结果表明：本文方法在局部点云和全局点云的精确配准效果均优于经典ICP算法，点云精确配准误差较小，且配准所耗时间显著减少。

图7 ICP点云精确配准Fig.7 Point cloud accurate registration with ICP algorithm

图8 全局配准后的点云结果Fig.8 Point cloud results after global registration

点云算法配准误差/mm耗时/s局部两帧点云经典ICP算法0.3970.206本文算法0.1890.187全局点云经典ICP算法0.6679.337本文算法0.2956.375

3.2.3 曲面重建及表面真实纹理贴图

在进行点云重建以后可以得到稀疏或稠密的地下井室点云重建结果，但是其仅停留于大量点集合的点云地图，3D点之间并没有明显联系，可视性较差；需要进一步的曲面重建还原出更为真实的实物原貌，增强可视化效果。本文在Windows 10环境下基于VS2017利用点云数据处理库(Point Cloud Libary, PCL)对重建的地下井室三维点云进行了曲面重建。图9所示为基于地下井室三维重建点云的泊松曲面重建结果。由重建的表面模型可以看到，经过泊松曲面重建后，在独立的3D点云间建立了一定的联系，目标表面的基本轮廓和形状都得到了很好的表达，模型的可视性明显提升。

图9 地下井室泊松曲面重建结果Fig.9 Poisson surface reconstruction results of underground wells

进行曲面重建后得到的模型缺少了彩色纹理信息，与实际场景的视觉效果存在一定的区别，可视化效果并未达到最佳，并未实现真正意义上的三维实景重建。为此，本文在重建的曲面模型的基础上，结合Kinect深度相机获取的彩色图像数据，通过纹理贴图重建出具有彩色纹理的模型。图10所示为地下井室场景模型纹理视图，可以看到,经过真实纹理贴图后的三维重建结果较之前的重建点云结果可视化效果更好，对于地下井室的局部纹理细节反映更细致，与实际场景基本一致。原始的三维点云重建结果只是大量彼此无联系的点云集合，由曲面重建方法可以实现将点上升到面的过程，获取三维重构模型，再通过真实纹理贴图还原出目标场景的真实面貌，实现真正意义上的三维可视化。

图10 地下井室纹理模型Fig.10 Texture model of underground wells

4 结论

本文提出了一种基于Kinect三维重建的地下井室可视化方法，通过Kinect v2.0从不同角度获取地下井室的深度及彩色图像数据，实现了地下井室的真实场景三维可视化。实验结果分析表明：

1)本文所提方法可使Kinect在0.5～4.5m的测距范围内，三维重建精度达到2cm；在4.5～7m的测距范围内，三维重建精度仍可保持在4.5cm以内。

2)针对Kinect深度测量误差提出了一种基于多项式曲面拟合的深度误差修正方法，可有效实现Kinect的深度测量误差修正。

3)实现了地下井室真实场景的三维可视化，获取了带纹理及细节特征的三维真实模型，可为地下井室三维探测和维护提供相应技术支持。