考虑UAV性能约束的变速度自主避障算法研究

周硙硙，赵海涛

(海军装备部驻南京地区第一军事代表室，南京 210001)

0 引言

随着科学技术的发展，无人飞行器(Unmanned Aerial Vehicle，UAV)智能化水平得到了很大地提升，无论在民用领域还是军事领域的应用都越来越广泛[1]。与此同时，UAV在执行任务过程中的安全性问题成为人们关注的焦点，特别是随着UAV执行任务的范围不断扩大和执行任务的环境日益复杂，其具备自主避障(Autonomous Collision Avoidance，ACA)功能变得尤为重要，且已成为智能化UAV的关键性能指标。为提高UAV执行任务的可靠性和降低执行任务的代价，为UAV配备性能良好的自主避障系统成为UAV技术研究的重要方向之一，而自主避障算法是自主避障系统的核心部分。对UAV而言，动态障碍避碰[2]成为一个重要的、普遍存在的、具有挑战性的问题。因此，如何提高UAV在复杂环境下执行艰巨任务的生存能力，成为UAV技术研究中亟待解决的关键问题之一[3]。

近年来，一些学者对UAV自主避障算法进行了深入研究，提出了基于速度障碍法的UAV自主避障算法，并取得了一些研究成果，提升了UAV自主避障系统的性能。学者P. Fiorini和Z. Shiller[4-5]提出了速度障碍法的理论框架；文献[6]将速度障碍法应用于多智能体的协同冲突消解；文献[7]在速度障碍法的基础上，提出了一种几何优化方法，以解决在融合空域内面临复杂障碍物时，UAV的飞行冲突解脱和航迹恢复问题；文献[8]为解决复杂融合空域内无人机冲突解脱过程中消耗大的问题，提出了基于速度障碍法的合作型无人机的最优防相撞策略；也有一些学者在速度障碍法的基础上，对其进行了延伸和拓展应用，文献[9]为解决UAV与UAV之间的自主避碰问题，提出了一种选择速度障碍法(Selective Velocity Obstacle，SVO)；文献[10]在UAV的非协同自主避障系统中应用了速度障碍法，并提出了一种感知与避碰速度障碍法(SA-VO)。

另外，还有一些学者将导引的思想引入威胁障碍物避碰的问题中，并提出了基于导引法的自主避障算法。文献[11]基于比例导引律提出了UAV的最优导引避障算法；文献[12]在非结构环境下，基于导引律方式实现了对威胁障碍物的避碰；H. S. Shin等[13-14]将微分几何的思想用于解决UAV的避障问题，提出了基于非连续导引控制律的避障算法；A. Mujumdar等[15]基于导引方式，给出了两种非线性避障导引方法：非线性几何导引(Nonlinear Geometric Guidance，NGG)及微分几何导引(Differential Geometric Guidance，DGG)，使UAV快速将向量对准瞄准点，并给出了相应的导引方法；文献[16]在动态环境下，提出了一种基于改进比例导引律的机器人动态避障算法。

文献[17]通过速度障碍圆弧对障碍物的威胁大小进行量化，提出了一种基于速度障碍圆弧法的UAV自主避障算法，解决了多动态威胁障碍物避碰、考虑潜在威胁障碍物对UAV避碰的影响以及动态不确定环境下自主避障的问题，但未对考虑UAV性能约束条件和变速率自主避障进行进一步研究。在考虑UAV自身性能约束的情况下，UAV在复杂动态环境下对威胁障碍的避碰将受到一定的限制，本文通过研究UAV速度矢量大小与威胁障碍速度障碍圆弧之间的关系，提出了一种考虑UAV性能约束的变速度自主避障算法。与现有算法相比，可实现UAV对威胁障碍避碰偏转更小的速度矢量角度，从而在考虑自身性能约束的条件下，为实现UAV对多威胁障碍的避碰提供了更大的避碰裕度，可有效地提升UAV在复杂动态环境下执行任务的安全性和可靠性。

1 UAV的自主避障模型

UAV在动态不确定环境下执行任务过程中，通常沿初始规划的航路飞行，初始规划的航路已完成对已知威胁障碍物的避碰。但UAV在跟踪规划航路的过程中，可能会遭遇未知的动静态障碍物，此时需要完成以下工作：1)对传感器感知到的动静态障碍物进行威胁性判断。2)若感知到所有的障碍物均不具有威胁性，则UAV沿初始航路继续执行任务；若感知到的障碍物中包含威胁性障碍物，则UAV需要对初始航路进行重规划。3)UAV沿重规划的航路继续执行任务，若再次感知到未知动静态威胁障碍物，则重复工作1)和2)，直至UAV完成被赋予的任务。

1.1 速度障碍模型的建立

UAV在执行任务的过程中，可通过自身携带的传感器装置获取障碍物O和自身的位置坐标、速度矢量等信息，即障碍物和UAV的位姿信息Pose2obs(PO,vo)、Pose2uav(PU,vu)。为简化避碰模型的建立，依据UAV与感知到的障碍物之间的大小关系，将UAV简化为质点，相应的障碍物确立为半径R的障碍圆⊙PO；那么，UAV和障碍物之间形成的障碍锥(Collision Cone，CC)如图1所示。其中，d0为UAV感知距离；l1和l2为障碍锥的边界，且为过UAV位置点PU并相切于障碍圆⊙PO的切线。

图1 障碍锥示意图Fig.1 Sketch of collision cone

(1)

(2)

考虑UAV对多障碍物避碰及潜在威胁障碍物对避碰影响的复杂情况，将障碍锥整体平移障碍物速度矢量vo得到速度障碍锥(Velocity Obstacle，VO)，如图2所示。在障碍锥模型上，UAV实现了对威胁障碍物避碰需要将与障碍物之间的相对速度vuo偏转出障碍锥；那么，从障碍锥转化到速度障碍锥后，可直接通过将UAV速度矢量vu偏转出速度障碍锥，从而实现对障碍物的避碰，简化了避碰模型的建立，特别是对多威胁障碍物及考虑潜在威胁障碍物影响的避碰分析。

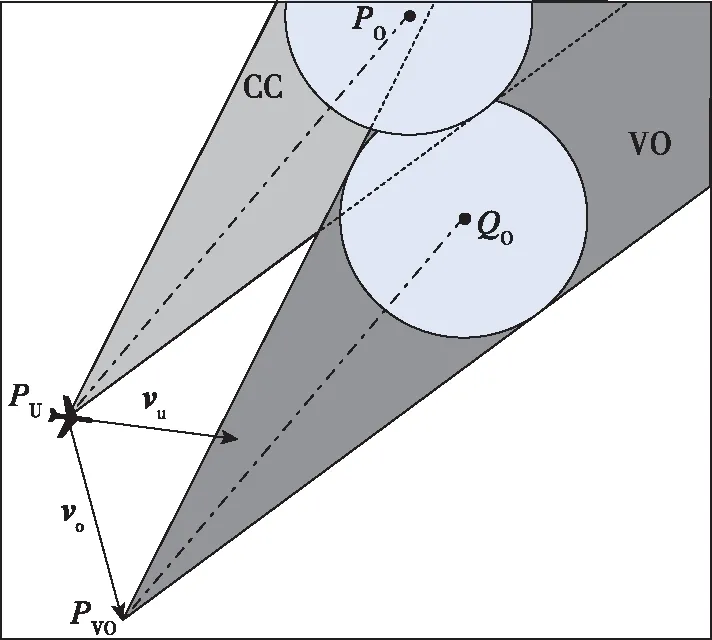
图2 速度障碍锥示意图Fig.2 Sketch of velocity obstacle

1.2 速度障碍圆弧法

速度障碍圆弧法的提出主要基于转化的思想，将障碍物对UAV的飞行安全影响转化为UAV速度圆⊙PU位于VO内的圆弧，称为速度障碍圆弧，如图3所示。那么，通过对速度障碍圆弧参数的计算，可将障碍物对UAV飞行安全的影响确定为UAV不可行的速度矢量方向范围，从而量化了障碍物对UAV飞行安全的影响，提升了UAV自主避障能力，特别是UAV对多威胁障碍物的避碰能力，同时也可综合考虑潜在威胁障碍物对UAV安全飞行的影响。

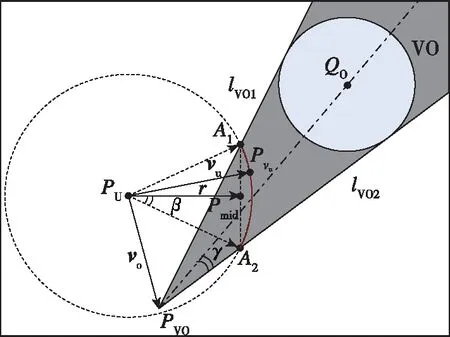
图3 速度障碍圆弧示意图Fig.3 Sketch of velocity obstacle arc

1.3 动态不确定环境下速度障碍圆弧法的应用

PVO+∈PVOQO

图4 动态不确定速度障碍模型建立的示意图Fig.4 Sketch of establishment of dynamic uncertain velocity obstacle model

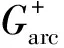
图5 动态不确定速度障碍圆弧示意图Fig.5 Sketch of dynamic uncertain velocity obstacle arc

2 考虑UAV性能约束的变速度自主避障算法

在复杂动态环境下，UAV可能遭遇多个动静态障碍物，单纯地通过UAV的速度矢量偏转实现对多个动静态障碍物的避碰较为困难，尤其在相遇的障碍物对应较大的速度障碍圆弧时，即UAV对应有一个较大的不可行飞行方向范围。较文献[17]在不考虑UAV机动性能的情况下，可实现对威胁障碍物的避碰；但复杂情况下，UAV要偏转较大的角度才能实现对威胁障碍物的避碰，此时UAV会偏离初始规划路径较大。那么对多威胁障碍物的避碰及考虑潜在威胁障碍物影响的情况下，变速度自主避障法将更具优势，且充分地考虑了UAV性能约束条件。

2.1 UAV动态性能约束条件

在考虑UAV动态性能约束条件时，依据UAV自身的机动性能，设定UAV法向加速度at和纵向加速度an的范围，则在有限自主避障时间tavo内，相应地UAV速度矢量vu具有一定的变化范围。

设定at和an的取值范围分别为

0≤at≤at_max

(3)

0≤an≤an_max

(4)

那么，在有限自主避障时间tavo内，UAV速度矢量vu的大小vu和方向角θu边界值可分别确定为

vu_min=vu-τ0

(5)

vu_max=vu+τ0

(6)

τ0=an_maxtavo

(7)

θu_min=θu-σ0

(8)

θu_max=θu+σ0

(9)

(10)

其中，r0为旋回半径，由UAV自身性能条件确定。则相应的UAV速度矢量vu的大小vu和方向角θu的范围可分别确定为

vu∈[vu_min,vu_max]

(11)

θu∈[θu_min,θu_max]

(12)

2.2 考虑UAV性能约束的变速度自主避障算法

为实现UAV在复杂动态环境下的安全飞行，且充分考虑自身的性能约束条件，基于速度障碍圆弧法，量化障碍物对应不同UAV速度矢量vu下的速度障碍圆弧Garc，再依据UAV速度矢量vu与速度障碍圆弧Garc之间的相对态势，从而确定UAV对威胁障碍物避碰的最优策略。以UAV对单个威胁障碍物避碰为例，考虑UAV性能约束的变速度自主避障策略态势如图6所示。

图6 考虑UAV性能约束的自主避障策略态势图Fig.6 Sketch of autonomous obstacle avoidance strategy considering UAV’s performance constraints

根据式(5)、式(6)、式(8)和式(9)，可确定UAV速度矢量vu的大小vu和方向角θu的约束范围分别为2τ0和2σ0。在态势图6中，分别以速度圆⊙PU最大半径vu_max和最小半径vu_min之间的差值、速度矢量方向约束范围线之间的夹角进行表示。相应的速度圆⊙PU以半径vu_min、vu和vu_max位于速度障碍内的圆弧可分别表示为

Garc-vu_min=⊙PU(λ=vu_min)∩VO

(13)

Garc-vu=⊙PU(λ=vu)∩VO

(14)

Garc-vu_max=⊙PU(λ=vu_max)∩VO

(15)

那么，从考虑UAV性能约束的自主避障策略态势图中可直观得出，UAV速度矢量方向角θu的约束范围限定了UAV在避障过程中的偏航范围，减少了UAV对威胁障碍物的避碰空间，尤其是UAV需要同时对多威胁障碍物进行避碰或考虑潜在威胁障碍物对避碰影响的情形。为解决考虑UAV性能约束条件下UAV避障空间变小的问题，基于偏航的思想实现了UAV对威胁障碍物避碰的方法，同时采取改变UAV速度矢量大小vu的思路进行研究。

对比态势图6中不同半径vu_min、vu和vu_max的速度圆⊙PU位于速度障碍内的速度障碍圆弧，可以确定UAV速度矢量大小vu改变了速度障碍圆弧在速度障碍上的相对位置和大小。假设UAV实现了对威胁障碍物避碰时速度矢量vu偏转的角度为λ，那么依据态势图6可以得出结论：

1)在有限自主避障时间tavo内，当UAV速度矢量vu通过逆时针偏转实现对威胁障碍物避碰时，UAV速度矢量大小vu变化为vu_min，对应的速度矢量vu偏转的角度λ最小，即

λvu_min<λvu<λvu_max

(16)

2)在有限自主避障时间tavo内，当UAV速度矢量vu通过顺时针偏转实现对威胁障碍物避碰时，UAV速度矢量大小vu变化为vu_max，对应的速度矢量vu偏转的角度λ最小，即

λvu_max<λvu_min<λvu

(17)

从而可通过比较λvu_min与λvu_max之间的大小，确定考虑UAV性能约束的变速度自主避障的最小速度矢量偏转角λmin，使得UAV偏离最优初始规划路径最小。因此，当UAV基于变速度自主避障时，UAV最小速度矢量偏转角λmin在速度矢量大小vu边界值上取得，且λmin小于UAV基于恒定速率避障的速度矢量偏转角度；则在偏转速度矢量避碰的基础上，辅以变速率的策略更加有助于UAV对威胁障碍物的避碰。

2.3 多威胁障碍物避碰方向分析

依据求解的速度障碍圆弧参数Garc，可将2个威胁障碍物的速度障碍圆弧表示在UAV的速度圆上，相应的示意图如图7所示。

图7 2个威胁障碍物的避碰圆弧示意图Fig.7 Collision avoidance arcs of two threatening obstacles

依据2个威胁障碍物的速度障碍圆弧参数Garc1(r1,φr1,β1)和Garc2(r2,φr2,β2)，可分别确定速度障碍圆弧对应的避碰不可行速度矢量方向范围为[φr1-β1,φr1+β1]和[φr2-β2,φr2+β2]。那么，2个威胁障碍物对UAV避碰所产生的不可行速度矢量方向范围为二者的并集。因此，为实现UAV对多威胁障碍物的避碰，需要将UAV速度矢量vu偏转出不可行速度矢量方向范围。为直观地确定UAV最优避障方向，将UAV速度矢量vu的方向角φu及2个威胁障碍圆弧所对应的圆心角范围表示在一维坐标系上，示意图如图8所示。从而，依据UAV速度矢量vu的方向角φu在UAV避碰的不可行速度矢量方向范围中的位置，可直观地确定UAV对2个威胁障碍物的最优避碰方向。

图8 2个威胁障碍避碰角度的坐标表示示意图Fig.8 Coordinates representation of collision avoidance angles for two threatening obstacles

3 算法的仿真与验证

在UAV自主避障态势图6中,给出了速度矢量大小vu边界值上速度障碍圆弧的情况，同样通过设定vu的取值范围，也可得出UAV速度矢量大小vu在取值范围内相对应的速度障碍圆弧Garc的大小；设定UAV法向加速度at和纵向加速度an的范围分别为[0,0.5]和[0,20]，本文以文献[17]中对威胁障碍物避碰仿真为例，作对比分析。

(1)单个威胁障碍物避碰

依据UAV性能约束条件，相应的UAV速度矢量vu的大小vu和方向角θu的取值范围可分别确定为[53.2,56.8]和[-10,136.8]。那么，对于任意的vu∈[53.2,56.8]，可确定一个速度障碍圆弧，即威胁障碍物对应于一个不可行UAV的速度方向范围；那么作出整个UAV速度矢量大小vu范围与速度障碍圆弧对应不可行速度方向范围的关系图，如图9所示。

图9 速度障碍圆弧对应的圆心角边界随UAV速率变化关系图Fig.9 Sketch of the relationship between the central angle boundary corresponding to velocity obstacle arc and the UAV’s speed change

在仿真图9中，给出了UAV性能约束条件对应的速度矢量大小vu的边界线，以及速度障碍圆弧在不同vu情况下对应的圆心角边界。那么，从图9中可以得出，威胁障碍物的速度障碍圆弧对应的圆心角边界随vu变化而改变，且在vu取值范围内，当vu取边界值56.8m/s时，UAV实现了对威胁障碍物避碰所需偏转的角度最小。

与文献[17]进行对比，对单个威胁障碍物避碰时UAV速度矢量所需偏转角度如表1所示。

表1 单个威胁障碍物避碰情况下的UAV避障方向角范围

那么，当UAV采取变速度自主避障算法时，对单个威胁障碍物避碰所需偏转的角度较小，较文献[17]避障算法性能更优，且更加易于实现。相应的UAV对单个威胁障碍避碰的仿真如图10所示。

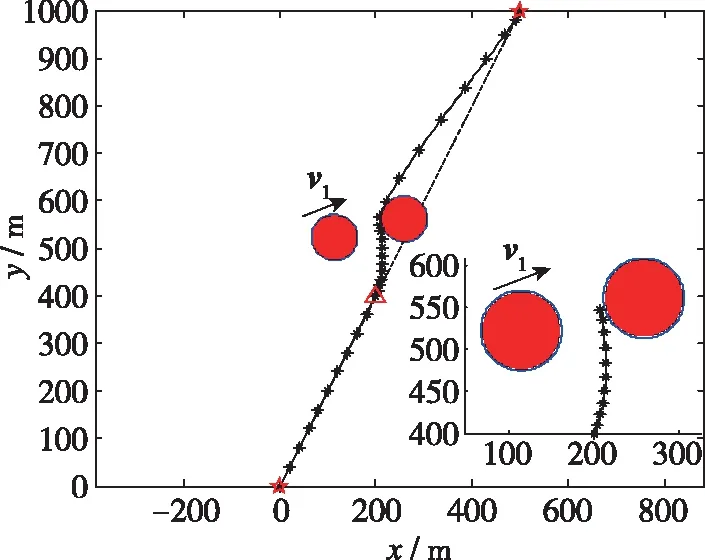
图10 UAV对单个威胁障碍避碰的仿真图Fig.10 Simulation diagram of single threatening obstacle avoidance for UAV

(2)多威胁障碍物避碰

当UAV需要对多个威胁障碍物进行避碰时，与文献[17]相比，UAV对多个威胁障碍物避碰的速度矢量所需偏转角度如表2所示。

表2 多个威胁障碍物避碰情况下的UAV避障方向角范围

那么，当UAV采取变速度自主避障算法时，对多个威胁障碍物避碰所需偏转的角度较小，较文献[17]避障算法性能更优，且更加易于实现。相应的UAV对多个威胁障碍避碰的仿真如图11所示。

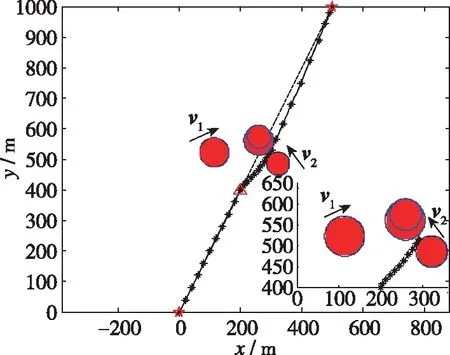
图11 UAV对多个威胁障碍物避碰的仿真图Fig.11 Simulation diagram of multiple threatening obstacles avoidance for UAV

4 结论

本文针对动态不确定环境下提升UAV执行任务的安全性和可靠性，提出了一种考虑UAV性能约束的变速度自主避障算法。算法分析和仿真结果表明：

1)考虑性能约束条件对UAV自主避障结果产生的影响。本文考虑UAV法向加速度约束，限定了UAV在自主避障时间内的速度矢量变化范围，更加贴近实际数学模型。

2)基于速度障碍圆弧法，得出障碍物对应的速度障碍圆弧大小和方向随UAV速度矢量大小变化，且在有限自主避障时间tavo内，UAV对威胁障碍物避碰的最小速度矢量偏转角λmin在速度矢量大小vu边界值上取得。

3)本文所提出的变速度自主避障算法为UAV避障提供了更多可能性，弥补了考虑UAV性能约束条件产生的限制。