被动型氢原子钟原子跃迁谱线测试与分析
陈煜舒,帅 涛,陈鹏飞
(1.中国科学院上海天文台,上海 200030;2.中国科学院大学天文与空间科学学院,北京 100049)
0 引言
被动型氢原子钟具有稳定度高、频率漂移率低、体积较小以及质量较小等特点,作为时间频率基准被应用于伽利略和北斗等卫星导航系统[1]。
根据量子力学理论,原子核外电子的能量不连续,一个原子从一个能级变换到另一个能级被称为跃迁,这个过程中原子对外以光量子或电磁波形式辐射或吸收能量,原子的能级不连续,因而原子跃迁的频率非常准确和稳定[2]。被动型氢原子钟通过(F=1,mF=0)到(F=0,mF=0)2个超精细能级的氢原子受激跃迁输出的1420.405MHz射频信号对压控晶振(Voltage Controlled Crystal Oscillator,VCXO)鉴频,通过后者输出高稳定度、高准确度的10MHz频率基准信号[3]。
高纯度的工业氢气通过镍管控制进入电离源电离,获得各个能态的氢原子,并通过准直器形成原子束流[4],由磁选态器筛选(F=1,mF=0)能级的氢原子进入储存泡。微波谐振腔和原子储存泡等设备构成的腔泡系统为这一能级的氢原子跃迁提供电磁环境,激励其跃迁到(F=0,mF=0)能级,输出稳定的1420.405MHz射频信号,这部分装置连同电磁屏蔽和真空系统等被称为氢钟物理部分(Physical Package,PP),而将原子跃迁谱线同步到压控晶振上的环路设备称为电路部分(Circuit Package,CP)[5]。
稳定度是原子频标最重要的指标之一,物理部分的性能直接决定了被动型氢原子钟的稳定度极限[6]。本文设计了测试电路对氢钟物理部分进行探测,利用物理部分的静态鉴频特性,获得了不同参数配置下的原子跃迁谱线。通过对谱线特性的分析,提出了使稳定度指标最优的参数配置方案,为物理部分与电路部分闭环参数的设置提供了依据。
1 氢原子跃迁谱线理论模型
原子跃迁谱线通常为洛伦兹线型(Lorentz Line Shape),其一般表达式为
(1)
其中,v为探测信号频率[2]。
对于被动型氢原子钟,当探测信号功率较高时,谱线线宽出现饱和效应,线型表示为
(2)
其中,S为饱和因子(Saturation Factor),反映了谐振腔内电磁场的强度,与弛豫时间(Relaxtion Time)相关,与输入功率正相关[6]。当谐振腔中心频率与原子跃迁频率一致时表示为S0。T2为氢原子横向弛豫时间,与储存泡结构、电磁场环境和氢气流量等相关。
原子跃迁谱线线宽定义为谱线功率衰减至峰值一半时的带宽,由式(2)得
(3)
定义原子受激跃迁辐射达到最大时的腔内微波信号与原子为受激跃迁时的腔内背景微波信号功率之比为增益
(4)
其中,b表示辐射最大时的腔内微波信号功率;p表示腔内背景信号功率;α为原子跃迁谱线的振荡系数,决定了系统的振荡特性,氢原子受激跃迁时,α<1[3-5]。
谱线增益反映了原子跃迁信号相对谐振腔的强度,而信噪比则进一步表征了原子跃迁信号相对环境噪声的强度,对于被动型氢原子钟物理部分的稳定度指标,有经验公式
(5)
即氢钟物理部分的稳定度与线宽和信噪比平方根之比成正比,稳定度越小,指标性能越好[5-7]。
2 测试电路设计
数字电路具有环路稳定性好、控制灵活性高的特点,基于此设计了对氢钟物理部分的测试电路[8],如图1所示。
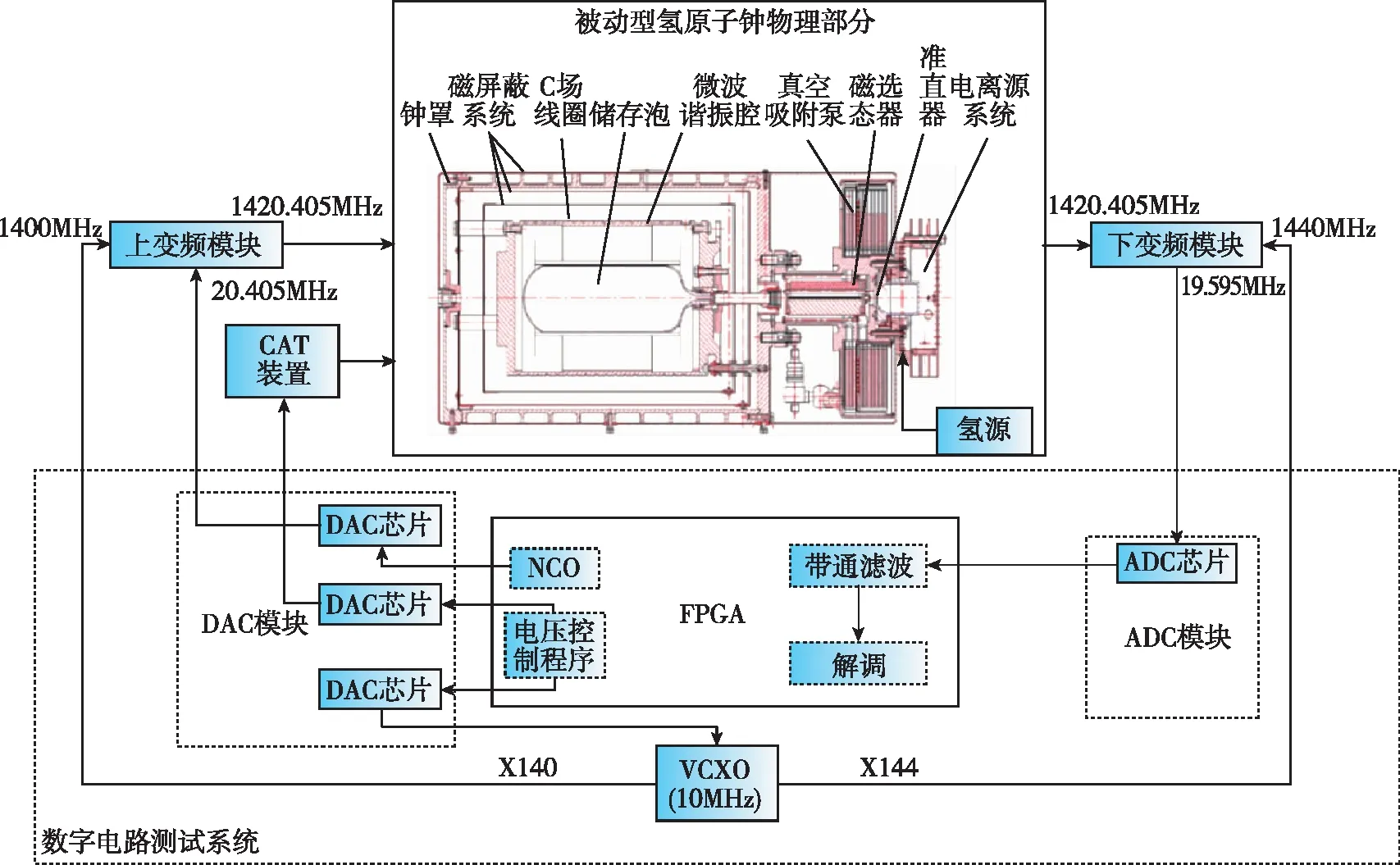
图1 测试电路原理图Fig.1 The schematic of the measurement and test circuit
被动型氢原子钟物理部分具有鉴频特性,在测试电路中作为鉴频器[9]。电路以现场可编程门阵列(Field Programmable Gate Array,FPGA)芯片为主控芯片,通过模数转换器(Analog-to-Digital Converter,ADC)和数模转换器(Digital-to-Analog Converter,DAC)等芯片及上下变频模块等实现了探测信号的产生、对谐振腔和压控晶振频率的控制以及原子跃迁谱线的采集、处理等功能。通过测试获得了多组不同参数下的谱线,测试结果可用于分析其特性。
2.1 探测信号的产生
探测信号由FPGA与DAC芯片输出的中频信号上变频后产生。
利用电子设计自动化(Electronic Design Automatic,EDA)工具对FPGA进行编程,实现数字控制振荡器(Numerically Controlled Oscillator,NCO)精确输出数字正弦信号。如图2所示,NCO的原理是正弦信号的幅度与相位线性相关,将其对应储存为只读内存(Read Only Memory,ROM)正弦信号幅度相位查找表(Look Up Table,LUT)[8-9],并设计相位积分器使得相位每遇到一个时钟上升沿就增加一个增量,即相位分辨率,再通过查找表获得其对应的幅度[10]。该数字正弦信号通过DAC芯片转换为模拟信号输出。由NCO和DAC组合输出模拟正弦信号的装置称为直接数字频率综合器(Direct Digital Synthesis,DDS),DDS输出信号频率fout为
(6)
其中,N为上升沿表深度,N=48;fs为数字系统参考时钟,fs=90MHz;频率分辨率达3.20×10-7Hz;查找表存储数据的位宽设置为16位;k为频率控制字,设置为63,818,980,972,094。为满足量化误差等方面的要求,通过14位DAC,DDS输出20.405MHz模拟正弦信号。
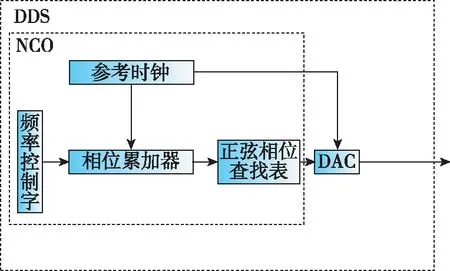
图2 DDS及NCO原理图Fig.2 The schematic of DDS & NCO
该20.405MHz中频信号在上变频模块与由晶振倍频的1400MHz射频信号混频后并通过高通滤波去除差频分量,产生与氢原子跃迁频率一致的1420.405MHz射频探测信号。
2.2 调谐电压的控制
利用EDA工具对FPGA编程输出两路线性扫描电压,分别对谐振腔频率和压控晶振频率进行控制。
微波谐振腔在氢钟工作时会发生腔牵引效应,即谐振腔中心频率偏离原子跃迁频率,这将造成测试结果的偏差[11]。扫描电压通过DAC芯片扫描腔自动调谐(Cavity Automatic Tunning,CAT)装置中的变容二极管,固定此路扫描电压为探测信号作用下的谐振腔幅度最大值所对应的值,从而抑制腔牵引效应[12-13]。
另一路扫描电压以同样的方式控制压控晶振频率,对晶振频率进行微调,但根据原子跃迁谱线特性,频率变化范围应大于跃迁谱线带宽但远小于谐振腔带宽[11],设置扫描频率更低、扫描区间更短。压控晶振振荡频率与控制电压具有线性关系,其作为上下变频模块的频率源,实现了对探测信号的线性频率调制。原子跃迁系统对不同频率探测信号的幅度响应不同,形成输出信号的包络。
两路扫描电压的扫描过程均在图3可视化。
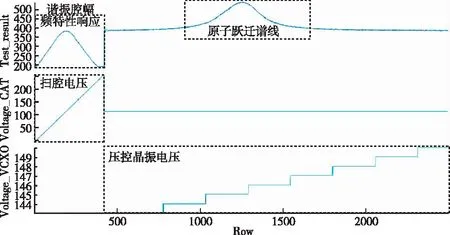
图3 典型测试结果Fig.3 Typical result of measurement and test
2.3 数据采集及信号处理
测试电路通过ADC芯片将下变频至19.595MHz的原子跃迁辐射信号采集到FPGA芯片进行处理。ADC芯片的有效位数由式(7)决定
(7)
其中,ENOB表示有效位数(Effective Number of Bits);SNRreal表示实际信噪比,单位dB。本文测试要求信噪比大于90dB,即ENOB为15位,而实际信噪比会比理想情况更差,故选择16位ADC[14]。
采集后的信号通过2MHz数字带通滤波器,获得幅度调制(Amplitude Modulation,AM)信号,可表示为
sm(t)=sI(t)·cosωct+sQ(t)·sinωct
(8)
其中,sm(t)为包络信号A[V(t)]与探测信号幅度调制后下变频的信号[14]。压控晶振频率与扫描电压具有线性关系:fvcxo∝V(t),故原子跃迁过程中的包络信号可表示为A(fvcxo)。
对于AM信号的解调有相干解调(Coherent Demodulation)和非相干解调(Noncoherent Demodulation)两种方式。非相干解调结构简单,但是其中的积分部分引起信噪比平方根衰减[16],不利于对信噪比的获取,故选择相干解调方案。相干载波由NCO提供,频率设定为19.595MHz,相干载波cosωct与AM信号sm(t)相乘
sp(t)=sm(t)·cos2π·ωct
(9)
对sp(t)低通滤波得到信号sd(t)
(10)
通过逻辑分析仪可以观察到sd(t),即原子跃迁谱线[15-17]。
3 测试结果分析
本文对上海天文台一台质量为23kg,品质因数(Q值)为6234的被动型氢原子钟物理部分进行测试,获得不同氢气流量和输入功率等参数配置下的原子跃迁谱线,典型测试结果如图4所示。其中,横坐标为采样点,由测试程序换算,测试结果两点之间的间隔等同0.01Hz带宽,而纵坐标的数字测量值与信号的电压成正比。

图4 谱线特性分析Fig.4 Analysis on properties of the spectral line
测试结果的增益G可以由式(11)得到
(11)
其中,Va表示测试得到的原子跃迁谱线峰值;Vc表示原子跃迁背景辐射强度,等于谐振腔峰值。
根据线宽定义,其所对应的测量值Vlinewidth为
(12)
利用拟合工具对测量结果进行拟合,式(12)计算结果对应的频率带宽即为原子跃迁谱线线宽。
表1测试数据为在不同参数配置下获得的谱线增益,单位为dB。
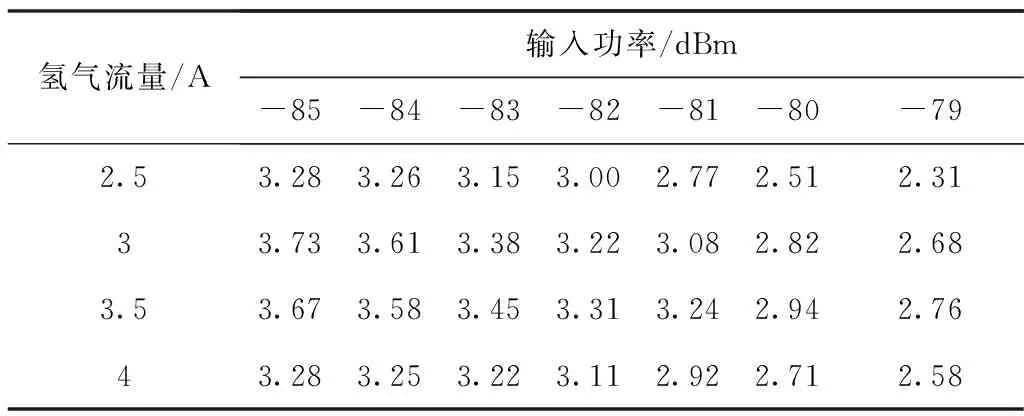
表1 不同参数配置下的谱线增益
对测试数据做趋势图分析,如图5所示。

图5 不同参数配置下的谱线增益Fig.5 Gains of spectral line in various parameters
由图5可知,谱线增益随输入功率增大而减小,随氢气流量先增大后减小。
表2测试数据为在不同参数配置下获得的谱线线宽,单位为Hz。

表2 不同参数配置下的谱线线宽
对测试数据做趋势图分析,如图6所示。
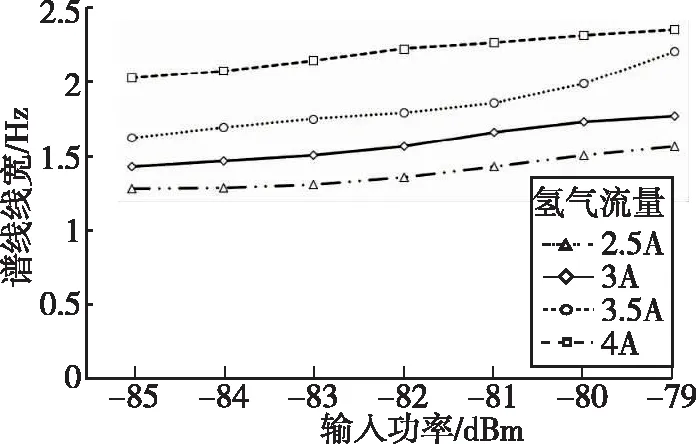
图6 不同参数配置下的谱线线宽Fig.6 Linewidths of spectral line in various parameters
通过图6可知,谱线线宽与输入功率和氢气流量均正相关。
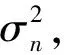
(13)

表3 不同参数配置下的信噪比
对测试数据做趋势图分析,如图7所示。

图7 不同参数配置下的信噪比Fig.7 The SNRs in various parameters
图7反映了信噪比与参数的关系,氢气流量和输入功率对信噪比的影响均不是单调的。
根据经验公式(5),定义参考值R
(14)
其中,式(13)中的信噪比使用信号与噪声比值的数值。对于同一环境的测试数据,通过比较R的大小判断其稳定度指标的优劣,R越大则稳定度指标越好。
图8所示为不同输入功率和氢气流量下测试得到的谱线R值,可以明显地观察到其在输入功率为-81dBm、氢气流量为3A时R值最大,即在此参数配置下频率稳定度指标最优。

图8 不同参数配置下的R值Fig.8 The R-values in various parameters
4 结论
物理部分性能决定了被动型氢原子钟产品的稳定度指标,本文设计了数字化测试电路对一台被动型氢原子钟的物理部分进行测试,并分析了不同参数配置下的原子跃迁谱线特性,获得以下结论:
1)输入功率越大,原子跃迁谱线增益越小,线宽越宽,信噪比先增大后减小,在-81dBm时达到最大值。
2)氢气流量越大,原子跃迁谱线线宽越宽。
通过稳定度与谱线特性的关系,提出了表4所示方案使得稳定度指标最优。

表4 最优参数设置方案
此后将对闭环后的氢钟进行稳定度测试,对此方案做进一步验证,力臻对物理部分参数配置的完善。

