管截面形状对颗粒毛细效应影响的离散元仿真
童亮 李美求 吕志鹏 陈帅挥
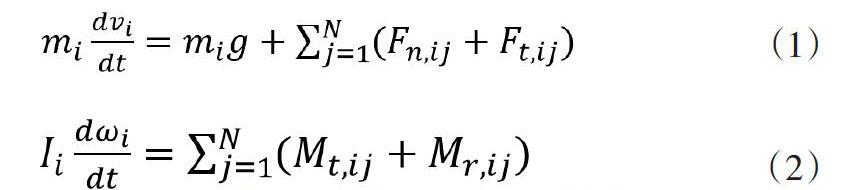

DOI:10.16660/j.cnki.1674-098x.2011-5640-4026
摘 要:垂直振動置于颗粒床的竖直空心小管,颗粒床中颗粒会沿竖直空心管向上攀升。本文将圆形截面管和等面积正六边形截面管置于同等振动强度、同种颗粒床内进行数值模拟,对比分析二者之中颗粒运动状态的异同点。给出了管内颗粒数量随时间的变化曲线,圆形截面管内颗粒数量在仿真结束前已经达到稳定,且要少于正六边形截面管内颗粒数量,除此之外正六边形截面管内颗粒数量有着很明显的上升趋势;通过观察两个时间周期内颗粒速度变化图,可知无论圆形截面管内颗粒是否达到稳定状态其速度场波动均较为剧烈,而正六边形截面管内颗粒速度场在处于稳定状态时明显要小于处于颗粒数量上升的状态;因此可以知道正六边形截面管在本文振动条件下有着比圆形截面管更好的运输能力以及运输稳定性。
关键词:颗粒 毛细效应 振动 逆重力运输
中图分类号:TQ022.3 文献标识码:A 文章编号:1674-098X(2021)01(c)-0050-05
Discrete Element Simulation of the Influence of Tube Section Shape on Capillary Effect of Particles
TONG Liang LI Meiqiu LV Zhipeng* CHEN Shuaihui
(Institute of Strength and Vibration of Mechanical Structures, Yangtze University, Jingzhou, Hubei Province, 434020 China)
Abstract: The vertical vibration is placed in the vertical hollow tube of the granular bed, and the particles in the granular bed will climb up along the vertical hollow tube. In this paper, the circular cross-section tube and the regular hexagonal cross-section tube with the same area are placed in the same vibration intensity and the same particle bed for numerical simulation, and the similarities and differences of particle motion state between the two are compared and analyzed. The change curve of the number of particles in the tube with time is given. The number of particles in the tube with circular section has reached a stable level before the end of the simulation, and is less than that in the tube with regular hexagon section. In addition, the number of particles in the tube with regular hexagon section has a very obvious upward trend. By observing the change diagram of particle velocity in two time periods, it can be seen that no matter the number of particles in the tube with circular section The results show that the fluctuation of velocity field is more violent when it reaches the stable state, and the velocity field of particles in the regular hexagon section tube is obviously smaller than that in the state of increasing number of particles when it is in the stable state; therefore, it can be known that the regular hexagon section tube has better transportation capacity and stability than the circular section tube under the vibration condition in this paper.
Key Words: Particle; Capillary effect; Vibration; Counter gravity transportation
离散颗粒在振动的条件下,会产生多种复杂的行为,如“巴西果效应(BNE)[1-3]”和反巴西果效、振动U形管中的颗粒迁移[4-5]。对插入颗粒堆中的空心管施加垂直振动,颗粒将沿着管上升,并最终在管内形成一个稳定的高度。这种特殊的逆重力运动现象为颗粒的输运方式提供了一种新的方式。其在运输颗粒物料方面结构简单、不易堵塞的特点,更为其在实际应用中增添了优势,考虑到工程实际的多样性,可以使用任意截面形状的管,因此研究管截面形状对颗粒传输特性的影响显得很有必要。
将竖直振动空心管插入装有颗粒的容器中,容器中颗粒会沿竖直管上升并在一段时间后与竖直管外颗粒形成一稳定的高度差。在2009年,Tatemoto等基于离散元(DEM)对这一现象进行了数值仿真,研究了管径大小对颗粒爬升高度、颗粒对流特性的影响[6];2014年,Liu等探究振动管管口形状对颗粒上升的影响;张富翁等设定颗粒床的竖直壁面为周期性边界,使用离散元方法模拟了第一个振动周期内颗粒的受力状况[7]。Liu与Zhao建立了颗粒上升高度与时间变化关系的半经验公式[8];2017年,Fan基于离散元模拟对其物理机制开展研究,发现了颗粒毛细效应的对流机制;Xu等同样采用离散元模拟方法,对管内沿轴线方向颗粒的填充率进行了探究,考察了振动条件、恢复系数对颗粒上升高度的影响[9-10];2018年,Zhang等通过实验,研究了振动强度和竖直管浸入深度对颗粒上升的影响[11];2019年凡凤仙等人对颗粒毛细效应现象进行了数值模拟,发现了颗粒毛细效应在此条件下呈现单周期上升、倍周期上升和倍周期稳定三个阶 段[13]。
考虑到蜂巢正六边形结构紧密坚固的特性,将同等截面积的圆管和正六边形管进行仿真计算,比较其不同。探究竖直管截面形状对于颗粒运输影响。
1 离散元法研究颗粒毛细效应现象
1.1 离散元法的数学模型
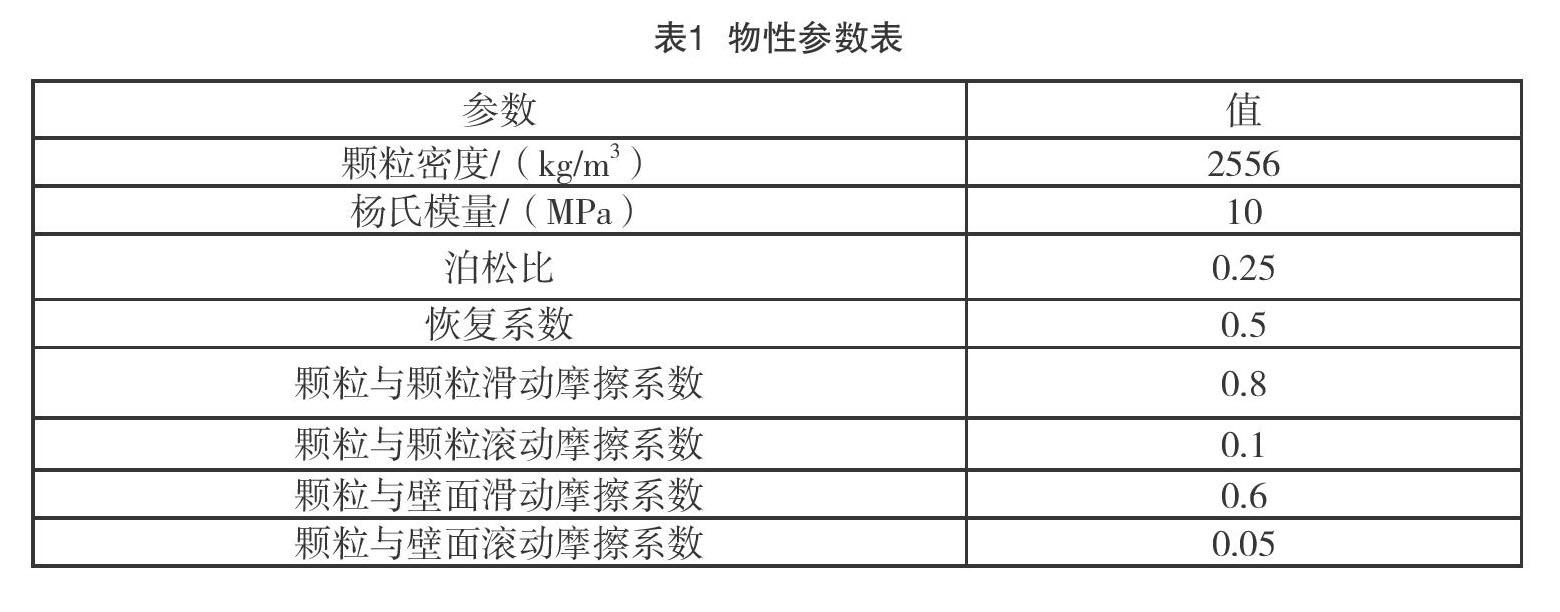
离散元方法研究离散颗粒体系的本质是将离散体系细化为单个颗粒的运动,然后将每一个颗粒运动联合起来,考虑单位时间步内颗粒之间的位移、碰撞、摩擦(参数见表1)。计算过程中法向力和切向力由下列方程控制。
(1)、(2)式子中mi和Ii分别为颗粒i的质量和转动惯量,vi和ωi分别是颗粒i的速度和角速度,g为重力加速度,t是时间,N为颗粒的数量,Fn,ij和Ft,ij分别是颗粒i和j之间的法相作用力和切向作用力,Mt,ij和Mr,ij分别是颗粒j的切向力对颗粒i产生的转矩和颗粒j的滚动摩擦力对颗粒i的转矩。
(3)式中ρ为弹性参数,δn,ij颗粒i和颗粒j之间法向重叠量。并且有δn,ij=Ri+Rj-|ri-rj|,Ri和Rj分别是颗粒i和颗粒j的半径大小,ri和rj为颗粒i和颗粒j的位置矢量。An为法向耗散系数,本文中依據与恢复系数ε的关系对An进行近似的计算。
(4)式中G为剪切模量,Y为杨氏模量,v为泊松比;At为切向耗散系数,μs、vt,ij和et分别是滑动摩擦系数、颗粒i和颗粒j的切向相对速度和切向单位矢量。
1.2 计算方法
本文设置竖直空心玻璃管竖直振动,频率f为10Hz,振幅为A为15mm。对应的无量纲振动强度。颗粒粒径r为0.6mm圆球形颗粒。设置不同管口形状的竖直空心玻璃管,分别为圆形、正六边形取圆管半径为3mm,正六边形管边长3.299mm,正四边形管边长5.317mm,管壁厚度均为0.6mm,保证各形状管截面积大小相等。实验中,设置浸入深度为40mm计算总时长为150个周期。
2 结果与讨论
图1给出了数值仿真开始前与结束时仿真结果图。截取沿y=0截面的剖视图。如图1为颗粒初始位置,通过张富翁等的研究[12]可知,管内颗粒初始高度并不影响最终颗粒高度。仿真过程中可以看到两个容器中颗粒床中心区域的颗粒在下降,位于容器壁周边的颗粒在竖直方向上明显要高于中心区域的颗粒,颗粒发生了对流现象[7]。
在垂直振动条件下,管外壁面对颗粒有剪切作用,促使容器内的颗粒出现对流,从而在容器中间区域形成对颗粒的横向运输运动,容器中部的颗粒随着管竖直振动过程的发生进入到竖直管中,周围颗粒不断向中部区域输送颗粒,管内颗粒不断增加,直到管下端产生的压力与管外颗粒在同一位置产生的压力相平衡时,颗粒系统趋于稳定,管内的颗粒不再增加形成基本稳定高度的颗粒柱[14]。
2.1 管内颗粒数量随时间的演变
为了更为直观的分析竖直管对于颗粒运输的能力,这里用管内颗粒数量来表征管对颗粒的运输能力。由图可知圆形截面管管内颗粒数量初始时刻有一个迅速的上升,管内颗粒数量在前25个周期时间段内一直保持上升经历一段时间的波动到第50个周期时刻管内颗粒数量再次迅速上升,在第80个周期时刻数量达到稳定,由此可以看到整个过程历经两个颗粒数量增加的时间段,最终达到稳定数量;六边形截面管内颗粒数量也在初始时刻有一个增加,但相较于圆管,它的初始上升时间较短并快速达到一个数量稳定的波动时间段,在第50个周期时刻颗粒数量第二次增加,上涨到与圆管内颗粒数量基本相同的数量,在第125个周期时刻,六边形截面管内颗粒数量有一个很明显增加;通过对比分析两种截面管内颗粒数量跟时间变化的关系曲线,能够知道六边形截面管在此振动条件下颗粒运输能力强于圆管。
2.2 管内颗粒的速度场
在20T-22T时间段内,根据图2曲线可知,管内颗粒数量均保持在一个稳定的数量内波动。在20T时刻,管向下运动,在20.25T时刻到达最低点,然后在20.5时刻再次通过初始位置,管带动颗粒向上运动,管上端颗粒拥有一个向上的速度。在20.75时刻,管到达最高点,此时速度方向将发生变化,对颗粒的剪切力方向发生改变。在21T时刻,管完成一个周期运动回到初始位置并向下运动,此时颗粒速度受到重力与管壁面剪切力作用,全部为向下运动。在21-22T时间段内,管周期性运动,带动管内颗粒运动。当颗粒被抛起过程中,颗粒间隙增加,壁面对颗粒剪切作用力会减小,其由主要受壁面剪切力变为主要受重力作用。分析20-22T两个周期内圆管和正六边形管内颗粒速度场变化,知道正六边形管在运动过程中颗粒间隙始终要小于圆管内颗粒。观察120-122T时间段内圆管和正六边形管内颗粒速度场,发现此时正六边形管内颗粒间隙相较于20-22T周期时间段内增大,结合图2颗粒数量随时间变化曲线,在120-122T时间段内,正六边形管内颗粒数量处在一个增长的时间段。由此分析,在颗粒数量增加的时间段,正六边形管内颗粒运动相较于颗粒稳定的时间段内颗粒运动更为剧烈。比较两个时间段内圆管和正六边形管内颗粒速度场变化发现,正六边形管内颗粒运动较圆管内颗粒运动要更加平稳。
2.3 管内颗粒能量变化
如图3为单个颗粒平均总能量随时间变化的曲线图,观察知圆管和正六边形管内颗粒能量变化,在初始时刻都有着明显的下降,然后回升,可以发现其变化趋势基本与图2中管内颗粒数量变化趋势相同。从图3圆管和截面管内颗粒能量变化曲线知道,正六边形管对颗粒有着更好的运输稳定性。且在计算最后时段,正六边形管内颗粒能量仍有着上升的态势,因此可以认为管内颗粒数量仍会继续上升,由此可以认为正六边形截面管对比同等截面的圆管对于颗粒的运输能力要更强。
如图3颗粒平均总能量随时间变化的曲线,可以看到曲线的分布与图一颗粒数量变化基本一致,由此可以知道,颗粒本身具有能量的多少决定管中颗粒数量。
3 结论
本文基于离散元法对比分析圆管和正六边形管在颗粒运输方面的异同点。给出了管中颗粒在运动各个时间段的速度场变化规律,分析了颗粒平均总能量与管中颗粒数量之间的变化规律。通过分析研究,得到如下结论:
(1)在相同振动强度、同种材料颗粒条件下,正六边形管对于颗粒运输能力要强于相同截面积的圆管。
(2)竖直管的截面形状不同导致对颗粒的运输能力也产生差异性,因此对竖直管管口界面形状的研究对于颗粒的逆重力运输有着重要的意义。
(3)相较于圆形截面管,正六边形截面管在振动过程中能量波动更为平稳,具有更好的运输稳定性。
参考文献
[1] Prziwara, P., Breitung-Faes, S., Kwade, A.: Impact of grinding aids on dry grinding performance, bulk properties and surface energy[J]. Adv. Powder Technol. 29(2), 416–425 (2018).
[2] Yamada TM,Katsuragi H. Scaling of convective velocity in a vertically vibrated granular bed. Planetary and Space Science,2014,100:79-86.
[3] Liao CC,Hsiau SS. Transport properties and segregation phenomena in vibrating granular beds[J]. KONA Power and Particle Journal,2016,2016(33):109-126.
[4] Gray, J.M.N.T.: Particle segregation in dense granular flows[J]. Annu. Rev. Fluid Mech. 50, 407–433 (2018).
[5] Sanchez I, Diaz AA,Guerrero B,et al. Improved model for the U-tube granular instability: Analytical solution and delayed coupling[J]. Mechanics Research Communications,2015,67:1-7.
[6] Yuji Tatemoto, Yuki Niwa, Takenari Takeshita,Circulation of particles in a vibrated bed with an inner tube[J]. Powder Technology,2009,:279-286.
[7] Liu CP,Zhang FW,Wu P,et al. Effect of hoisting tube shape on particle climbing[J]. Powder Technology,2014,259:137-143.
[8] Liu Y,Zhao J. Experimental study and analysis on the rising motion of grains in a vertically-vibrated pipe[J]. Chinese Physics B,2015,24(3):030405.
[9] Fan FX,Parteli EJR,Poschel T. Origin of granular capillarity revealed by particle-based simulations[J]. Physical Review Letters,2017,118(21):218001.
[10] Fan FX,Liu J,Parteli EJR,et al. Vertical motion of particles in vibration-induced granular capillarity[J]. EPJ Web of Conferences,2017,140:16008.
[11] Zhang FW,Cronin K,Lin Y,et al. Effects of vibration parameters and pipe insertion depth on the motion of particles induced by vertical vibration[J]. Powder Technology,2018,333:421-428.
[12] 張富翁,王立,刘传平,等.竖直振动管中颗粒的上升运动[J].物理学报,2014,63(1):14501.
[13] 韩红,姜泽辉,李悠然,等.器壁滑动摩擦力对受振颗粒体系中冲击力倍周期分岔过程的影响[J]. 物理学报, 2013 ,62(11):114501.
[14] 刘举,白鹏举,凡凤仙,等.竖直振动下颗粒物质的行为模式研究进展[J].化工进展,2016,35(7):1956-1962.
[15] Zhang N,Cheng B,Baoyin H. A new physical model on the capillary phenomenon of granular particles[J]. Applied Mathematics and Mechanics(English Edition),2019,40(1):127-138.

