基于卡尔曼滤波算法的自平衡机器人检测分析

易强 宋子瑜

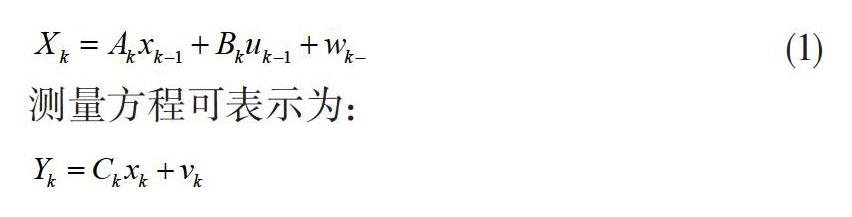
DOI：10.16660/j.cnki.1674-098x.2101-5640-2708

摘  要：对立方体机器人姿态的检测也是立方体机器人能够实现单点平衡的重要一环。姿态检测反映了立方体机器人平衡时的姿态角，当立方体机器人姿态角发生改变时，自平衡控制系统接收到姿态角的改变而做出反应，调整动量轮转速转向来保证立方体机器人平衡。将传感器安装在立方体方块上时，随着立方体方块姿态的变化可获得稳定的翻滚角和俯仰角，基本实现立方体机器人的姿态角测量。

关键词：姿态检测  机器人  姿态传感器  姿态角  卡尔曼滤波器

中图分类号：TP242.2                        文献标识码：A                  文章编号：1674-098X（2021）03（c）-0001-4

Detection and Analysis of Self Balancing Robot Based on Kalman Filter Algorithm

YI Qiang1   SONG Ziyu2

（1.Suzhou Ruisai Precision Tools Co.， Ltd， Suzhou， Jiangsu， 215104 China; 2. School of Automation， Beijing Institute of Technology， Beijing， 100102 China ）

Abstract： The attitude detection of the cube robot is also an important part of the single point balance of the cube robot. Attitude detection reflects the attitude angle of the cube robot when it is in balance. When the attitude angle of the cube robot changes， the self balancing control system responds to the change of the attitude angle and adjusts the rotation speed of momentum wheel to ensure the balance of the cube robot. When the sensor is installed on the cube， the stable roll angle and pitch angle can be obtained with the change of the cube attitude， and the attitude angle measurement of the cube robot is basically realized.

Key Words： Attitude detection; Robot; Attitude sensor; Attitude angle; Kalman filter

立方體自平衡机器人主要分为以棱边平衡的机器人和以角平衡的机器人，以棱边平衡的机器人只需要一个动量轮即可进行单边平行，而以角为平衡点的机器人需要三个相互垂直的动量轮[1]。因此以角为平衡的机器人应用空间更大，但是难度更高[2]。

自平衡机器人开发的难点在于自身姿态的平衡保持，姿态平衡最重要的就是要确定立方体机器人当前的姿态角，只有正确的姿态角才能保证立方体机器人对动量轮的控制能够达到立方体机器人的单点平衡。若借助固定的检测系统（摄像机）来对立方体进行检测，会由于立方体机器人的不断运动，造成数据的不准确、丢失等问题[3-4]。

立方体的检测系统应当属于自身，这样的检测系统减少数据传输过程中的丢失问题，同时使立方体姿态角的实时性更好[5-6]。

1  卡尔曼滤波器设计

卡尔曼滤波的信号模型可以分为状态方程和测量方程两个部分。卡尔曼滤波通过递归计算的方法用上一时刻的估计值和当前时刻的测量值来计算当前时刻的估计值。卡尔曼滤波器的离散系统信号模型的状态方程可以表示为：

测量方程可表示为：

式中Xk表示k时刻的系统状态量，Yk表示k时刻的观测变量。wk表示系统的测量噪声，vk表示系统的观测噪声，具有独立正态分布，其符合期望值为0。uk-1是k-1时刻的可控向量，Ak、Bk、Ck是k时刻的增益矩阵并由系统决定。

在这个条件下卡尔曼滤波器通过测量方程（2），从第一个时刻观察到第k个时刻，这k个观察值分别为Y（1），Y（2），...，Y（n），第j时刻的状态X（j）由这k个观察值进行估计，并结合线性代数与统计知识，得到卡尔曼滤波算法的5个核心公式。事实上，卡尔曼滤波算法分为两个部分，第一个部分为预估，当前时刻的估计值由上个时刻的估计值得出。第二部分为校正，用当前时刻的观察值校正预测值，以此提高估计值的精确性。

（1）预估过程

（2）校正过程

a）滤波增益计算

预估过程中通过k-1时刻的估计值Xk-1去预估k时刻的状态值Xk-，同时由k-1时刻的协方差Pk-1和过程噪声的协方差来预测此时k时刻的协方差Pk-。而校正过程则是先求出k时刻的卡尔曼增益Kk，然后通过公式（5）和（6）来校正k时刻的估计值Xk和协方差Pk。卡尔曼滤波算法的流程如图1所示：

2  線性模型建立

首先，建立测量系统模型，即陀螺仪姿态角测量的线性模型。本设计立方体机器人绕着自身所在的坐标系旋转的角速度作为陀螺仪的输入量，立方体机器人的姿态角作为有效输出。不考虑误差，陀螺仪输出的角速度与立方体的姿态角存在如下关系：

式中θ（k+1）为立方体在k+1时刻姿态角，θ（k）为立方体在k时刻的姿态角，ω（k）为立方体在k时刻绕自身坐标系旋转时的角速度，△t为系统的采样周期，v（k）为系统的过程噪声。

事实上在计算物体姿态角的过程中应当考虑陀螺仪测量的误差对测量结果的影响，因此最后的关系式应为：

式中err（k+1）是陀螺仪在k+1时刻的测量误差。

实际上陀螺仪的测量误差并不是一个常值，这是一种具有时变性质的误差。设定陀螺仪的测量误差与陀螺仪所测的角速度以及上一时刻的误差线性相关，即：

式中δ是陀螺仪测量误差err（k）与输入的ω（k）之间的一种线性关系。

接下来结合（9）和（10）可以得到陀螺仪测量的最终模型为：

接下来把立方体的姿态角θ（k）和陀螺仪的测量误差err（k）作为系统状态，把加速度ω（k）作为系统的输入量，那么陀螺仪的线性测量模型可以变成表示如下的状态方程：

令

可以得到姿态角测量系统的状态方程为：

对于姿态角而言，加速度计的角度输出值可以表示为：

因为陀螺仪的输出值不会受到加速度计的检测状态的影响，所以加速度计的误差输出值为0。所以由检测系统的状态变量X可知，姿态角的输出可以表示为：

令

则式（14）可以表示为：

式中C为系统的观测矢量。

卡尔曼滤波器在式（13）和（16）的基础进行设计，用加速度计输出的翻滚角和俯仰角修正陀螺仪的姿态角测量误差，从而提高姿态角测量的准确性。

3  数据融合

姿态角测量的数据融合主要分为以下几个步骤：

计算测量的偏差值

计算陀螺仪所需的横滚角φG、俯仰角θG的预估值与加速度计测量的横滚角φA、俯仰角θA之间的偏差值。计算表达式如下：

式中errφ、errθ分别为横滚角φ和俯仰角θ在k时刻的偏差，也就是校正值。

（2）计算卡尔曼增益K

其中，P（k-1）为k-1时刻的协方差，C（k）为系统输出方程的观察矢量，R（k）为测量噪声协方差。

由下式得出：

（3）修正姿态角的系统预测值

通过式（16）可得出卡尔曼增益以，由式（17）（18）来修正系统姿态角的最终输出值：

滤波协方差P（k+1）算法更新

在完成了k时刻的计算后应该更新系统的滤波协方差，这样可以保证算法的递归计算、不断循环，其计算公式为：

定义一系列变量，陀螺仪的噪声协方差Qangle为0.001，陀螺仪的漂移噪声协方差Qgyro为0.003，加速度计的测量噪声协方差Rangle为0.5，滤波器采样周期△t为0.005。完成定义后根据五个公式在keil 5中建立响应的模型，将加速度和陀螺仪所测量的姿态角输入卡尔曼滤波器中进行数据融合。计算出最优角度、最优飘零，更新角度测量模型模型。

4  结论

本文研究了单点自平衡立方体的姿态检测，设计了立方体的姿态检测系统对姿态角进行检测，为立方体单点平衡的研究打下基础，选择姿态角数据融合的方法，选用卡尔曼滤波器进行数据融合，通过卡尔曼滤波器利用加速度计的姿态角对陀螺仪的姿态角进行修正。

参考文献

[1] Marle C M. Symmetries of hamiltonian systems on symplectic and poisson manifolds[J]. Lecture Notes in Applied and Computational Mechanics， 2018， 50（13）： 2033-2049.

[2] Yin S Y， Ou Y P， Dai X， et al. An Adaboost based face detection system using parallel configurable architecture with optimized computation[J]. IEEE Systems Journal， 2017， 11（1）： 260-271.

[3] Zhang Z F， Sarlette A， Ling Z H. Integral control on Lie groups[J]. Systems and Control Letters， 2019， 80： 9-15.

[4] Hu C L， Gong L Y， Wang T J， et al. Effective human age estimation using a two-stage approach based on Lie Algebrized Gaussians feature[J]. Multimedia Tools and Applications， 2019， 74（11）： 4139-4159.

[5] Altuzarra O， Diez M， Corral J， et al. Kinematic analysis of a flexible tensegrity robot[J]. Mechanisms and Machine Science， 2017， 46： 457-464.

[6] YUANXF，XIANGYZ，WANGY，et al.Neural networks based PID control of bidirectional inductive power transfer system[J].Neural Processing Letters，2020，43（3）：837-847.