基于物料运动特性和破碎机理的旋回破碎机生产率分析
王林伟,高 勇,宋伟刚,刘 宇
1东北大学机械工程与自动化学院 辽宁沈阳 110819
2北方重工集团有限公司 辽宁沈阳 110000
旋 回破碎机应用于煤矿、冶金建材等行业的初级破碎阶段,是中粗碎矿石的典型机械设备。为预测旋回破碎机的性能、优化腔型以及为研制新型旋回破碎机提供理论根据,对旋回破碎机生产率计算方法的研究具有重要意义。国内外学者已对破碎机生产率的计算进行了深入研究:Briggs 分析了散体物料在动锥上的受力及运动特性,推导了圆锥破碎机的生产率计算模型[1];Evertsson 基于散体物料和动锥运动学和动力学特性,建立了圆锥破碎机的生产率计算模型[2-5];郎宝贤等人[6]根据动锥每转一周排出的一个环形体积的物料,结合物料物理参数计算旋回破碎机的生产率;黄冬明[7]结合 Evertsson 的研究成果,提出了动锥在高转速下物料以自由落体方式通过破碎腔的圆锥破碎机生产率计算新方法;李强等人[8]基于物料运动特性建立动锥在低转速下物料滑动模型,提出了旋回破碎机生产率计算的新方法。
目前对旋回破碎机生产率的研究大多基于物料以自由落体的方式通过破碎腔,未考虑物料以滑动方式通过破碎腔。而在实际生产中动锥转速不同,物料通过破碎腔的运动方式亦不同,直接影响破碎机生产率。相对于细碎圆锥破碎机,中粗碎旋回破碎机的破碎比较大,挤压破碎力大,若采用高转速,衬板磨损速度加快,破碎机寿命降低,因此物料在旋回破碎机中多以滑动运动方式为主。
笔者对物料在挤压和排料半周期的运动特性进行研究,推导物料的运动方程,并采用数值计算方法求解。依据物料运动特性和层压破碎机理,建立动锥在低转速下物料以滑动方式通过破碎腔的旋回破碎机生产率计算模型。最后以 PXF6089 旋回破碎机为例,通过离散元法仿真和现场测量试验,验证该旋回破碎机理论生产率计算模型的可行性。
1 散体物料通过破碎腔的运动方式
1.1 旋回破碎机腔型结构分析
如图 1 所示,PXF6089 旋回破碎机的动锥衬板由直线段和曲线段组成,曲线段又由 18 段直线段相连而成。为便于研究,建立以悬挂点为原点O,竖直方向为Y轴的全局坐标系。当动锥对称中心线和Y轴重合时,取曲线段上各直线段端点作为拟合点,采用最小二乘法构造正则方程组,运用 Gauss 消去法求解得到二次拟合函数各项系数。动锥拟合曲线如图 2 所示,在全局坐标系下动锥母线函数式为
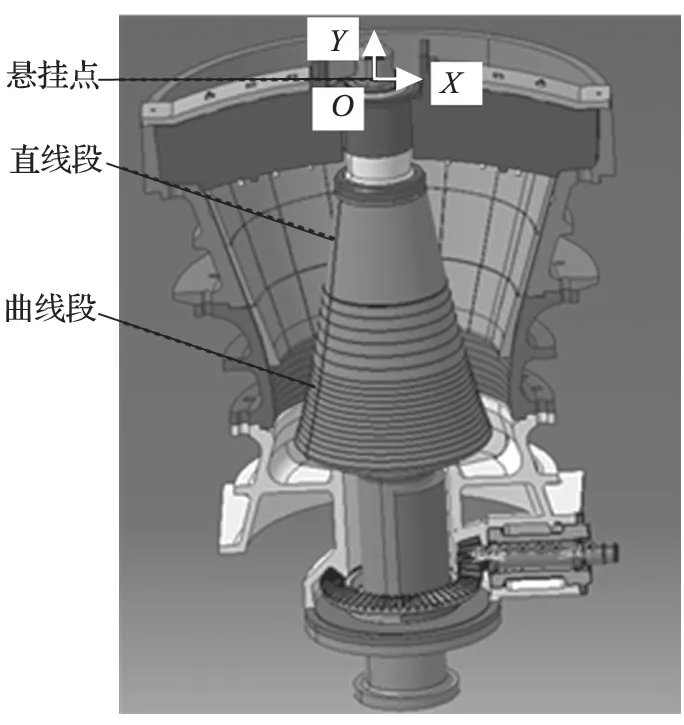
图1 PXF6089 旋回破碎机三维图Fig.1 3D diagram of PXF6089 gyratory crusher
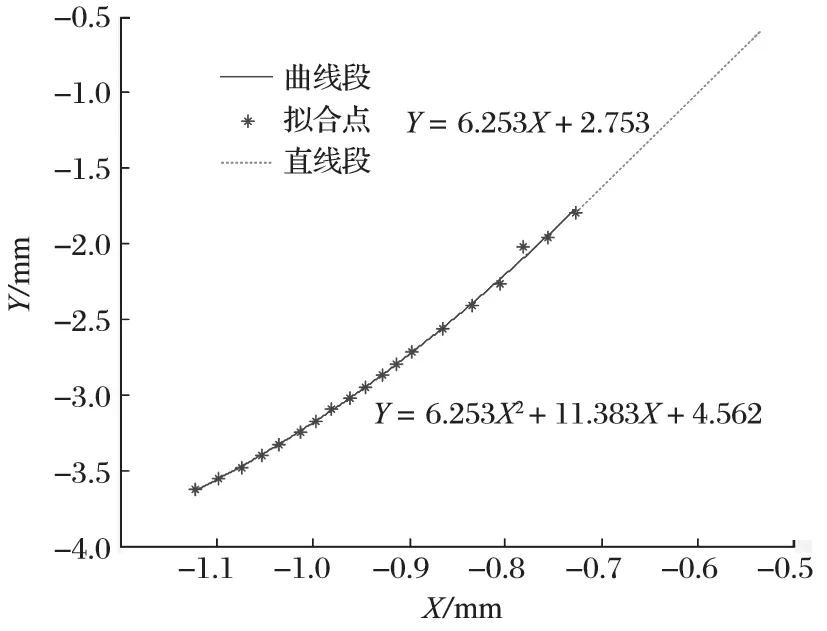
图2 动锥拟合曲线Fig.2 Fitting curve of moving cone

式中:am、bm分别为动锥直线段斜率和截距,m;cm、dm、em分别为动锥曲线段拟合二次项系数、一次项系数和常数项,m。
1.2 散体物料的运动方式分析
物料通过破碎腔的运动方式主要取决于动锥转速及动锥在挤压和排料极限同一位置的高度差。其运动方式分为自由落体、滑动运动以及 2 种运动方式并存3 种。
如图 3 所示,在给料口,物料在A点与动锥衬板接触,假设物料发生自由落体运动,将在B点与动锥再次接触,则物料自由下落距离为hmin;同理,在排料口处,物料自由下落距离为hmax,其中hmax>hmin。若物料在破碎腔内每个旋回周期都发生自由落体运动,则物料在重力作用下的位移应小于hmin,即动锥转速应大于物料发生自由落体运动的临界速度nc2;若每个周期内物料都发生滑动运动,则物料的位移应大于hmax,即动锥转速应小于物料发生滑动运动的临界速度nc1。因此旋回破碎机动锥的临界转速模型为
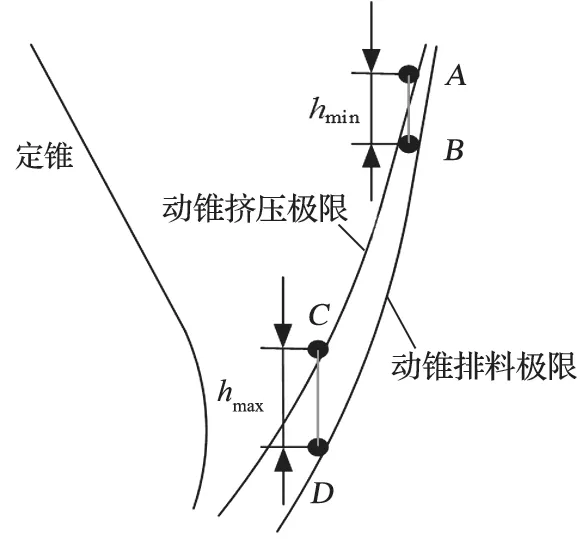
图3 动锥的临界转速模型Fig.3 Critical speed model of moving cone

式中:hmax、hmin分别为动锥在挤压和排料极限同一位置高度差的最大和最小值,m。
根据动锥挤压和排料极限位置方程求得hmax=0.178 m,代入式 (2) 得出 PXF6089 旋回破碎机物料发生滑动运动的临界速度nc1=157.5 r/min。该破碎机推荐的动锥转速n=120 r/min,因此,物料通过破碎腔的运动方式为滑动运动。
2 旋回破碎机生产率计算
2.1 生产率建模
为了预测 PXF6089 旋回破碎机的生产性能和进行腔型优化,需要基于物料运动特性和层压破碎理论,建立动锥在低转速下物料以滑动方式通过破碎腔的旋回破碎机生产率计算模型。
如图 4 所示,根据物料滑动和随动锥衬板旋摆上拱的运动特性,将堵塞层截面分为排料和挤压半周期,在动锥转角α处任取微元进行二重积分,可分别计算出排料和挤压半周期的排料量Qdown及上拱量Qup,两者之差即为旋回破碎机的生产率,如式 (3)~(5) 所示。

图4 堵塞层截面物料的运动分布Fig.4 Motion distribution of material on cross section of clogged layer
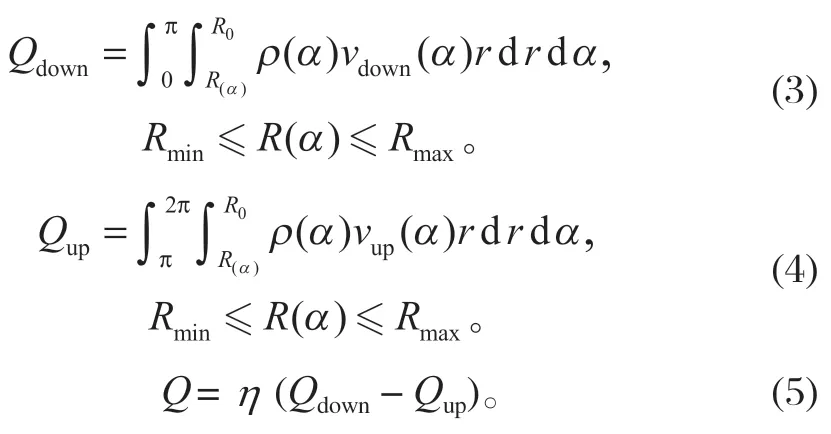
式中:R0为定锥半径,m;R(α) 为动锥椭圆上的点到定锥中心距离,m;ρ(α) 为堵塞层物料堆积密度,t/m3;vdown(α) 为堵塞层截面排料半周期的下落速度,m/s;vup(α) 为堵塞层截面挤压半周期上拱速度,m/s;η为单位时间,h。
由生产率计算模型可知,一旦知道堵塞层截面排料和挤压半周期的下落速度和上拱速度的表达式,便可通过积分求出旋回破碎机的生产率,因此需对排料和挤压半周期的物料运动特性进行分析。
2.2 排料半周期物料运动特性分析
虽然动锥在空间上做旋回运动,但从纵截面上看,动锥上的各点都是以悬挂点为圆心、以到悬挂点的距离为半径的单摆运动,最大摆角为进动角的 2倍。因此,排料半周期内物料沿动锥衬板滑动下落的同时,随着动锥绕悬挂点摆动。
2.2.1 相对坐标系的建立
为研究排料半周期的物料和破碎机的运动特性,以悬挂点为原点,以动锥对称中心线为y轴,建立如图 5 所示相对坐标系Oxy。相对坐标系与全局坐标系的夹角为θt(以顺时针方向旋转为正),相对坐标系的摆动角速度、角加速度分别为ω、˙ω,挤压极限处对应的时间t=0。
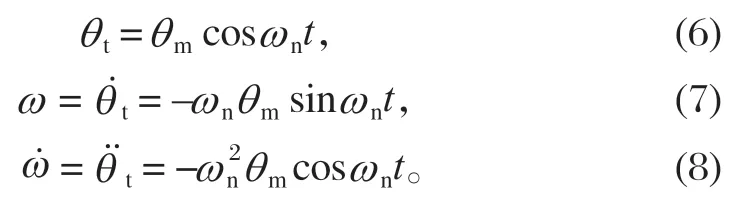
式中:θm为最大摆角,rad;ωn为动锥角速度,rad/s。
2.2.2 受力分析
如图 5 所示,任取第i破碎层中靠近动锥衬板的单颗粒物料为研究对象,物料沿动锥衬板表面滑动下落时受到自身重力G、摩擦力Ff和动锥衬板对它的支持力N的作用。支持力N与摩擦力Ff的合力用Nres表示,将Nres和G在相对坐标系中进行正交分解,根据牛顿第二运动定律可得到物料的受力平衡方程为

图5 单颗粒物料受力分析Fig.5 Force analysis on single particle

式中:γ为摩擦角,rad;ψxy为支持力N与y轴之间夹角,rad。
消去式 (9) 中Nres,可得在相对坐标系下绝对加速度ax与ay的关系为
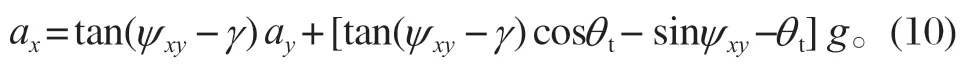
2.2.3 加速度分析
如图 6 所示,物料沿摆动的动锥衬板滑动下落时,将产生相对速度vr和相对加速度ar;物料与动锥衬板重合的A点绕悬挂点摆动时将产生牵连加速度ae,切向与法向分量分别为和ω×(ω×r),大小为r˙ω和rω2;当牵连运动是转动形式时会产生科氏加速度ac,矢积为 2ω×vr,方向采用右手定则确定。根据加速度合成定理可得物料在相对坐标系下的绝对加速度为
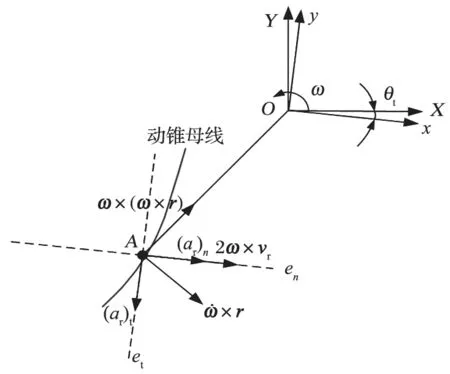
图6 物料加速度分析Fig.6 Analysis on material acceleration

对式 (11) 进行矢量积计算后,可得相对坐标系下的绝对加速度aa的表达式如式 (12)、(13) 所示。
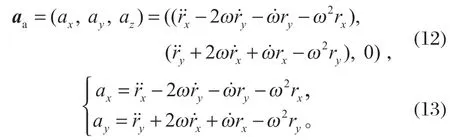
2.2.4 运动方程的推导
只要物料与动锥衬板接触,ry就完全由rx和动锥衬板母线函数fgeo决定。因此,式 (13) 中ry、和rx之间具有以下关系:
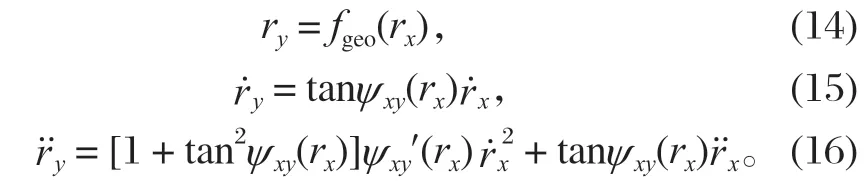
将式 (13)~ (16) 代入式 (10),可推导出物料滑动运动方程为

令q=tan (ψxy-γ),则式 (17) 可以化简为
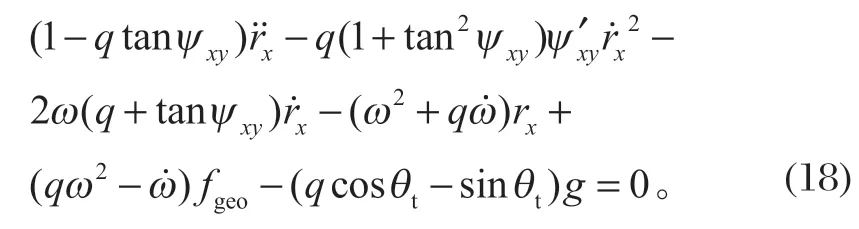
由式 (18) 可知,该运动方程是关于rx为自变量的二阶非线性微分方程。为求解该方程,对于每个位置的rx,fgeo、tanψxy、的值必须为已知,而这些值是由动锥衬板母线函数提供的。
2.2.5 运动方程的求解
当相对坐标系和全局坐标系重合时,将式 (1) 中的X、Y替换成rx、ry,可得此刻的动锥母线在相对坐标系下的函数。尽管动锥母线在全局坐标系下作旋摆运动,但在相对坐标系下却保持相对静止,因此在任意时刻动锥母线在相对坐标系下的函数fgeo保持不变,如式 (19) 所示。

如图 7 所示,ψ xy为支持力N与y轴之间的夹角,根据几何关系,ψ xy等于动锥母线在该点的切线与x轴的夹角,即切线在相对坐标系下的倾斜角,因此ψxy的函数为

图7 几何关系Fig.7 Geometric relationship

令vx=,将二阶非线性微分方程式 (18) 转化为一阶微分方程组,即
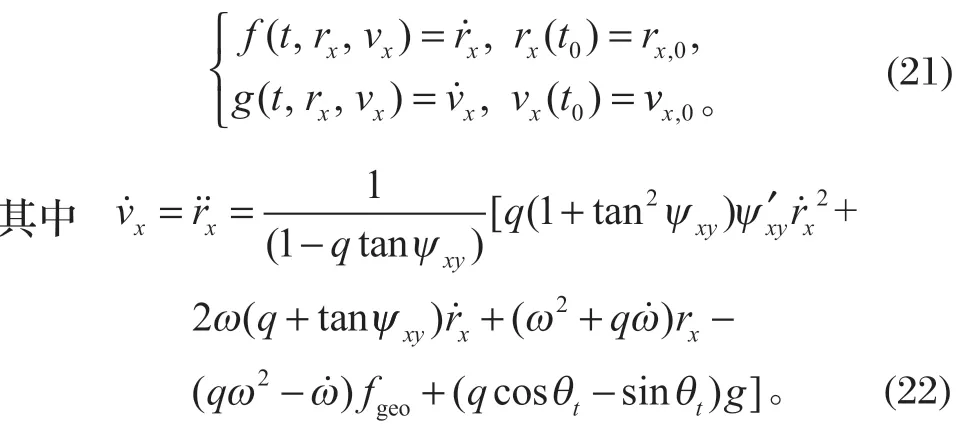
采用四阶标准 R-K 方法对一阶微分方程组求解,过程如下:

对任意给定的时间步长 Δt,经过多次迭代求出rx、和后,与之相关的ry、和可通过式 (14)~ (16) 求得。
当动锥母线上A点相对坐标 (rx,ry) 已知,通过坐标变换,可计算出A点的全局坐标。因此,在全局坐标系下可绘制物料在破碎腔中的滑动运动轨迹。
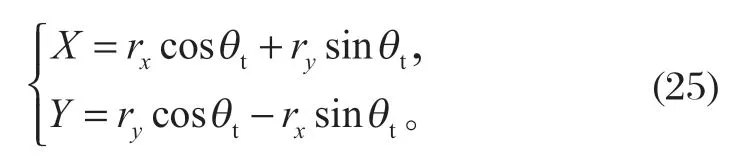
2.2.6 下落速度vdown(α) 的求解
由式 (13) 可计算出在相对坐标系下的绝对加速度ax和ay,必须将其变换到全局坐标系下,如图 8 所示。由式 (26) 可得物料在Y轴方向的加速度aY,当时间步长 Δt特别小时,可认为物料在每个步长内的aY恒定。在整个排料半周期内,物料作变加速度的加速滑动运动,任意时刻的下落速度vY,n+1通过式 (26)、(27) 迭代计算出,再将其与动锥转角α采用最小二乘法进行二次拟合,可得物料在任意转角α处的下落速度vdown(α),如式 (28) 所示。
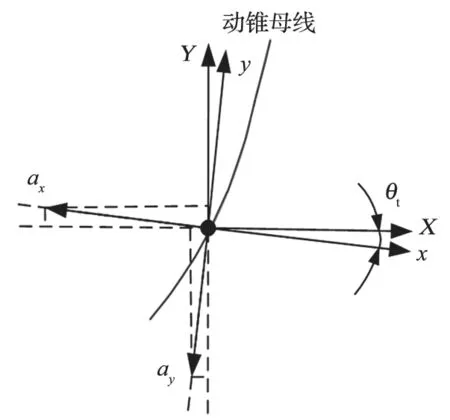
图8 全局坐标系下的绝对加速度Fig.8 Absolute acceleration in global coordinate system
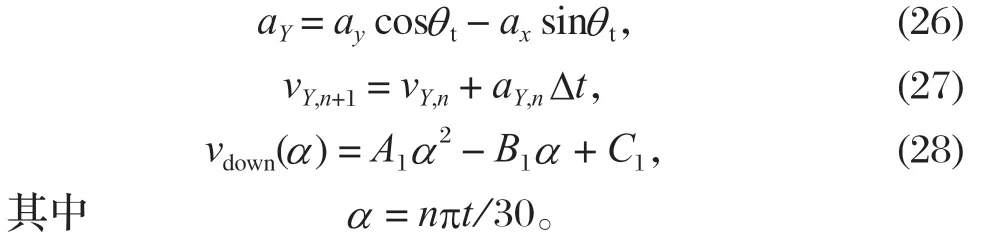
式中:A1、B1、C1为拟合系数。
2.3 挤压半周期物料运动特性分析
物料滑动下落后会立即随动锥衬板旋摆上拱,破碎腔中的物料被紧密压实,无向下运动趋势,因此,挤压半周期内物料只作单纯的单摆运动。(XB,YB) 为单摆起点坐标,则物料单摆终点坐标 (XC,YC) 为
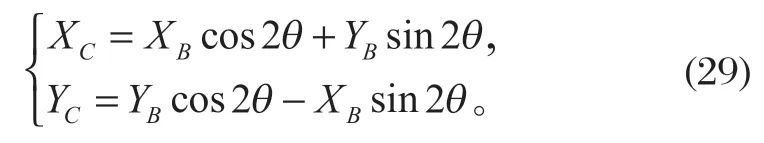
式中:θ为进动角,rad。
如图 9 所示,物料上拱速度与相应位置动锥上拱速度一致,转角α处物料的上拱速度vup(α) 沿径向为线性分布,与定锥接触处物料速度最小,与动锥接触处物料速度最大,即

图9 物料上拱速度分布Fig.9 Distribution of upwards creeping speed of material

式中:vd为摆动速度,m/s;τ为摆径与X轴夹角,rad。
在任意半径r处物料上拱速度
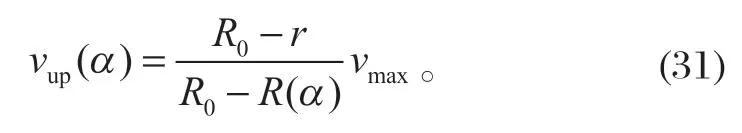
2.4 旋回破碎机理论生产率算例分析
以 PXF6089 旋回破碎机为例,对生产率进行计算。PXF6089 旋回破碎机生产率计算参数如表 1 所列。
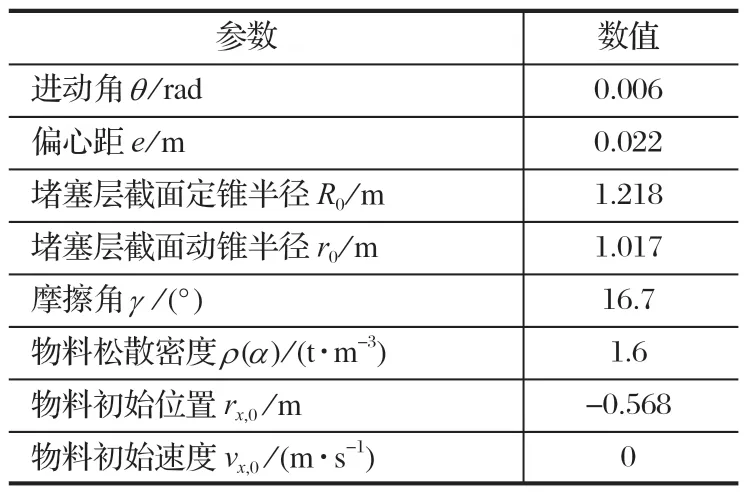
表1 PXF6089 旋回破碎机生产率计算参数Tab.1 Parameters of calculating productivity of PXF6089 gyratory crusher
若满足给料充分、给料粒度均匀和给料可破碎性等要求,即可确保物料在旋回破碎机破碎腔中实现层压破碎,而不是传统的单颗粒破碎。
旋回破碎机的破碎层可根据破碎腔中单颗粒物料的运动轨迹来划分,这样既考虑了旋回破碎机本身的运动特性,同时又考虑了物料在破碎腔中的运动特性。具体分层方法:根据式 (25) 和式 (29) 可绘制破碎腔中单颗粒物料的运动轨迹,如图 10 所示。A点为单颗粒物料的初始点,B点和C点为物料随动锥绕悬挂点的摆动轨迹BC与动锥母线的交点,过C点作摆动轨迹切线,切线与定锥母线相交于D点,则切线DC与摆动轨迹BC共同构成了当前破碎层的边界线。散体物料在动锥直线段经过 3 次层压破碎,在曲线段经过 4 次层压破碎,最后一个破碎层为堵塞层。

图10 物料运动轨迹Fig.10 Motion trajectory of material
根据式 (28)、(31) 对堵塞层物料竖直方向速度进行绘制,如图 11 所示。在排料半周期内,物料作变加速度的加速下滑运动,下落速度vdown(α) 随转角α的增大而增大;在挤压半周期内,动锥的上摆具有简谐运动特点,上拱速度vup(α) 呈现出简谐运动的规律。

图11 堵塞层物料竖直方向速度Fig.11 Speed of material on clogging layer in vertical direction
将堵塞层物料的下落速度vdown(α) 和上拱速度vup(α) 代入动锥在低转速下的生产率模型 (式 (3)~(5)),计算出理论生产率Q=4 052.992 t/h。
3 生产率离散元法仿真验证
为确保旋回破碎机生产率计算模型的可行性,采用离散元法进行仿真验证。
近年来,EDEM 软件被广泛应用于破碎领域并取得了良好效果。Potyondyd 提出了一种用粘结颗粒模型 BPM (Bonded Particle Model) 模拟矿石破碎过程的先进手段,该模型具有较好的数值计算特性[9]。Quist 和Evertsson 等人[10-13]都通过大量试验验证了 BPM 的准确性。使用 EDEM 软件采用 Hertz-Mindlin 和 BPM 模型对旋回破碎机矿石破碎过程进行离散元仿真分析。
3.1 仿真模型建立
对旋回破碎机关键零部件进行建模,简化与仿真无关零部件。根据某选矿企业提供的矿石给料粒度曲线,将矿石粒度离散化处理,采用均匀分布方式确定各矿石颗粒的大小和数量,采用模具挤压法,按照矿石实际的几何形状形成由填充颗粒构成的矿石模型,在 EDEM 软件后处理模块中导出填充颗粒的位置坐标及半径,将其写入 API 文件中的替换颗粒坐标数据文件和颗粒替换文件,具体过程如图 12 所示。

图12 仿真模型建立Fig.12 Establishment of simulation model
3.2 仿真计算过程
3.2.1 参数设置
仿真破碎过程主要分为 3 个阶段:颗粒替换、粘结键形成及粘结键断裂,如图 13 所示。为确保仿真的可靠性,需对矿石模型粘结键参数进行标定。Quist采用夹逼处理的方法,以矿石宏观力学特性为目标,对细观参数进行标定[14]。采用 EDEM 软件模拟矿石单轴压缩试验的方法来标定铁矿石模型的粘结键参数,如表 2 所列。材料属性和材料间接触属性根据资料和文献设定[15],分别如表 3、4 所列。
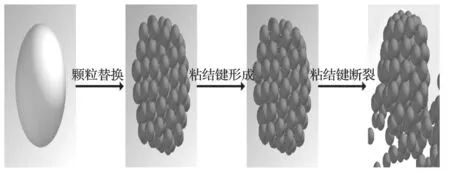
图13 仿真破碎过程Fig.13 Simulation of crushing process
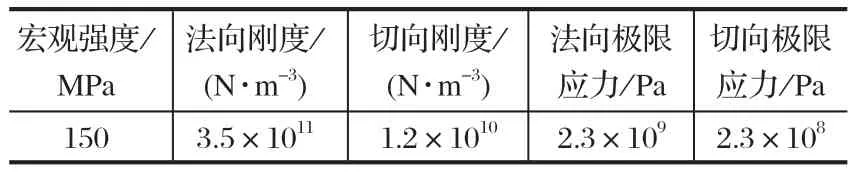
表2 矿石力学参数Tab.2 Mechanical parameters of ore

表3 材料属性Tab.3 Material properties

表4 材料间接触属性Tab.4 Contact properties of material
3.2.2 仿真过程
选取固定时间步长 (Rayleigh 步长的 5%),文件自动保存时间间隔为 0.01 s,仿真时间为 15 s,文件大小为 10~ 30 GB。仿真过程如图 14 所示。

图14 仿真过程Fig.14 Simulation process
3.3 仿真结果分析
在 EDEM 软件后处理模块中将质量传感器放置于集料槽处,以统计集料槽内破碎产品的质量。
由图 15 可知,产量曲线分为 4 个阶段:初始阶段 (0~ 0.85 s),包括物料生成、颗粒替换和落入破碎腔;产量不平稳阶段 (0.85~ 3.13 s),只有少许物料以单颗粒破碎形式破碎;产量平稳阶段 (3.13~ 10.24 s),物料完全进入破碎腔并以层压破碎形式破碎,产量平稳增加;最终阶段 (10.24~ 15.00 s),破碎腔内剩余的物料以单颗粒破碎形式被逐渐破碎。取产量平稳阶段作为计算对象,采用平均生产率计算公式

图15 产量随时间变化曲线Fig.15 Variation curve of throughput with time

式中:Q(t1)、Q(t2) 为不同时刻生产量,t。计算得出平均生产率Qa=3 715.20 t/h。
为了更好地分析旋回破碎机生产率,需对导出的产量数据进行相应后处理工作:使t2~t1趋于很小的值,按照式 (32) 计算得出的生产率为瞬时生产率。根据计算结果绘制瞬时生产率随时间的变化曲线,如图16 所示。

图16 瞬时生产率随时间变化曲线Fig.16 Variation curve of instantaneous productivity with time
由图 16 可知,瞬时生产率曲线也分为 4 个阶段:初始阶段,瞬时生产率为 0;生产率上升阶段,大量粒度小于破碎机排料口尺寸的物料未经破碎直接被排出,导致生产率激增;生产率波动阶段,生产率在 3 700~ 4 200 t/h 之间小幅波动;生产率下降阶段,破碎腔中物料逐渐减少,导致生产率逐渐降低。
4 现场测量试验验证
为进一步验证该生产率模型的可行性和可靠性,对某选矿厂 PXF6089 旋回破碎机的生产率进行现场测量。如图 17 所示,现场测量试验包括物料卸载、破碎起始、破碎终止和产量测量。在输送带托辊下方安装称重传感器 (皮带秤),用于实时测量和记录破碎产品质量。经过近一年的记录,实际测量的 PXF6089旋回破碎机生产率为 3 600~ 4 100 t/h。

图17 现场测量试验Fig.17 Field test
将 PXF6089 旋回破碎机生产率理论计算值、离散元仿真值和现场测量数据汇总,如表 5 所列。

表5 PXF6089 旋回破碎机生产率汇总Tab.5 Summarization of productivity of PXF6089 gyratory crusher t/h
由表 5 可知,PXF6089 旋回破碎机生产率理论计算值略大,这是由于生产率计算模型是基于层压破碎理论建立的,它满足充分给料、给料粒度均匀、给料可破碎性等基本前提和假设,是一种理想的工作状态,该数值在仿真和现场测量的可行域中,验证了该生产率理论计算模型的可行性。
5 结论
(1) 对物料在挤压和排料半周期的运动特性进行研究,推导了物料的运动方程,并采用数值计算方法求解。
(2) 依据物料运动特性和层压破碎理论,提出了根据单颗粒物料运动轨迹对旋回破碎机腔型分层划分方法,建立了动锥在低转速下物料以滑动方式通过破碎腔的旋回破碎机生产率计算模型。
(3) 采用 EDEM 软件进行仿真分析和实际生产测量,验证了低速旋回破碎机理论生产率计算模型的可行性,但该模型是基于层压破碎理论建立的,是理想工作状态,造成理论值偏大,可视为 PXF6089 旋回破碎机的最大生产率。

