黄河流域城市土地利用全要素生产率指数的偏向型技术进步分析及收敛性检验

薛建春，张安录

（1.内蒙古科技大学 经济与管理学院，内蒙古 包头014010；2.华中农业大学 公共管理学院，湖北 武汉430070）

一、引言

伴随社会经济与城市化的发展，人地矛盾日益突出，土地作为重要生产要素之一，其相关研究由来已久。自生态文明的思想提出以后，土地利用相关研究内容也日渐丰富，而且，城市土地资源、粗放城市建设、保护生态环境与偏向型技术进步之间关系愈加紧密。2015年李克强总理在政府工作报告中强调：增加研发投入，提高全要素生产率，将推动中国经济由投入型增长转向效率型增长。因此本文立足城市土地利用全要素生产率指数，研究偏向资本、劳动的技术进步与偏向土地资源的技术进步对城市土地利用全要素生产率指数的影响。[1](p36-47)

新古典增长理论假设资本和劳动两种投入要素之间的替代弹性为1，技术进步表现为中性，[2](p131-142)但在实际生产过程中，技术进步对于要素的偏向型不同导致技术进步具有方向性。技术进步对土地利用的影响主要表现为技术进步通过要素边际产出，进而影响土地利用生产率，所以，技术进步作为土地利用生产率的来源之一，其偏向型会直接影响土地利用过程中要素的投入和对环境造成的影响。学者们普遍认为偏向型技术进步起源于J.R.Hicks的宏观经济假设——诱发性创新，目的是为了节约更珍贵的要素资源，[3]张俊回顾了偏向型技术进步的研究进展，总结偏向型技术进步理论是将技术进步方向的内生化，用于解释现实生活中许多经济现象，激励环境友好型技术的进步。[4](p148-160)技术进步偏向型理论最初用于探索技术进步在资本与劳动之间的优化配置对收入的影响，后来应用于资本与劳动之间的替代弹性研究，[5](p62-82)[6]近几年应用领域更为广泛，Zhou 分析了我国不同类型环境规制对能源环境偏向型技术进步的影响，[7](p1-23)Yi，Ming 以中国30 个省市2003—2016年的面板数据为实证，分析了中性技术进步和偏差技术进步对雾霾污染的影响，发现不同类型技术进步的减霾效果存在显著区域差异性，[8](p169)陈勇利用省级面板数据，分析了技术进步偏向、资本与劳动要素禀赋、产业结构变动对劳动收入份额发生的逆转作用，[9](p56-68)韩国高实证检验了技术进步偏向对工业产能过剩的影响程度及其传导机制，发现技术适宜性下技术进步偏向会有效促进生产效率并化解产能过剩，[10](p2157-2167)丁黎黎发现技术进步是中国沿海地区海洋积极绿色生产率增长的主要驱动因素，且呈现节约资本、使用劳动和资源的特征。[11](p119-127)

综上，以往学者很少将偏向型技术进步引入土地资源利用中，而且在测算技术进步偏向性时大多采用参数法，可能会影响结果的稳健性。因此，总结相关研究成果，选用基于方向距离函数的Super-SBM 模型结合Window-Malmquist 指数模型计算城市土地利用全要素生产率指数，并分解其来源得到投入偏向、产出偏向和规模变化技术进步指数，探究黄河流域城市土地利用的技术进步偏向是节约土地资源亦或是减少资本或劳力投入，并分析土地利用全要素生产率指数的收敛特性，为流域内城市土地利用决策提供建设性建议。

二、研究方法与数据来源

（一）研究区域概况。

黄河流域地处我国西北部，途经9省69个地级市，虽然幅员辽阔，但其主要的黄土地貌和干旱、半干旱气候使得整个流域内水土流失严重，黄河“水少沙多、水沙异源”的突出特征对沿途城市的生态治理提出了更高要求。流域内69 个城市的常住人口21749.9万人，占全国人口总量的15.54%，土地面积218.3万平方公里，占国土面积22.74%，GDP总量130683.18亿元，占全国经济总量的13.25%，近四分之一的土地面积经济总量却不足七分之一，土地利用生产率低下成为黄河流域发展的瓶颈。在当前黄河流域生态保护与高质量发展的引领下，在我国目前还不能一蹴而就的工业化转型发展期内，一项创新研发的新技术可以偏向于减少土地投入且促进土地利用生产率提高，因此识别投入与产出的技术进步偏向性，可以合理地节约土地资源且保护环境，促进黄河流域生态保护与高质量发展。

（二）研究方法。

将方向性距离函数Super-SBM 模型与Window-Malmquist 指数模型相结合，测度黄河流域土地利用全要素生产率指数，并在此基础上进行技术进步的偏向性分析和收敛性检验，探索黄河流域土地利用全要素生产率指数变动的内部驱动机制。

1.Super-SBM模型。

传统的距离函数没有考虑非期望产出的影响，本文选用包含非期望产出的Super-SBM 模型计算城市土地利用全要素生产率指数，考虑到规模报酬可变条件下SBM模型存在无可行性解的状态，选用规模报酬不变包含非期望产出的Super-SBM模型，其数学规划模型如下：

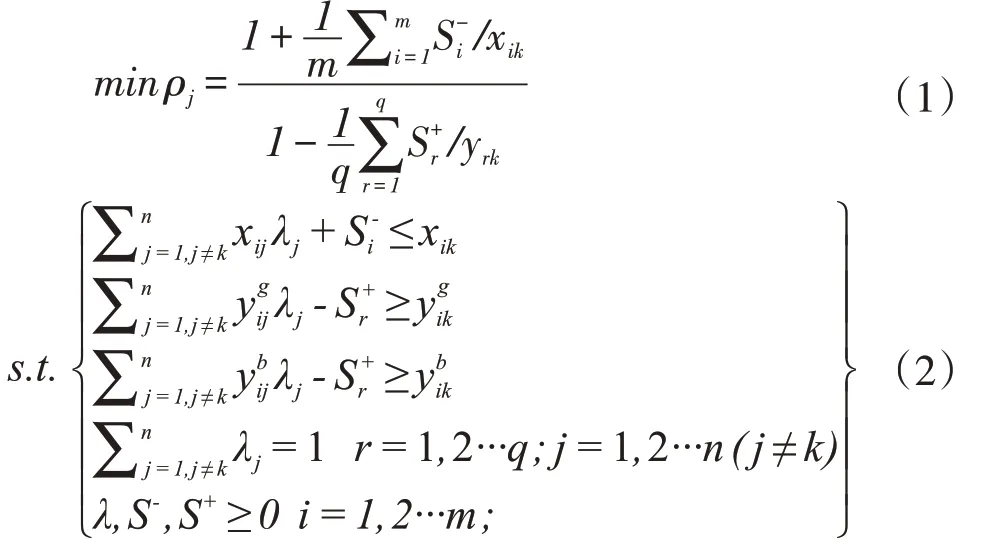
其中，ρj为评估的指数值，S-，S+分别表示过度投入与产出不足。记为期望产出，记为非期望产出。

2.Window-Malmquist指数模型。

由于Malmquist 方法得到的指数值无法按照时间序列纵向对比，[12](p56-68)[13](p1345-1355)本文引入Windows变体，在这种模式下，不同时期的每个决策单元可以视为不同的单元，对处理小样本数据非常有效，为了反映土地资源和投入要素施加给土地利用的影响，本文选用包含非期望产出的投入产出指标，采用基于投入角度的Window-Malmquist 模型将土地要素也纳入偏向型技术进步研究中，测算黄河流域城市土地利用全要素生产率指数，然后分解得出效率变化和技术进步导致的增长率改变。效率变化指数（EC）表示投入产出组合到生产前沿面之间距离的变化，技术变化指数（TC）表示生产前沿面本身的变化情况。由于选择几何平均的分解方法，[14](p220-229)所以，进一步将技术变化指数分解为投入偏向型技术变化（IBTC）、产出偏向型技术变化（OBTC）和技术规模变化（MATC）指数。将Window模型窗口宽度设置为最大，相当于所有时期的“DMU”汇总成一个总参考集，计算Malmquist 全要素生产率指数，然后通过公式（3）分解其来源得到投入偏向、产出偏向和规模变化技术进步指数，进而分析黄河流域城市土地利用技术进步的偏向是土地资源节约（土地资源投入的相对减少）或者是土地环境保护（土地利用碳排放的相对减少）。Malmquist指数公式表示如下：

IBTC 反映了技术进步对各投入要素边际替代率的改变，IBTC＞1 说明投入偏向型技术进步使得全要素生产率在投入要素等比例减少的情况下增加；OBTC 反映技术进步对多种产出不同比例的促进作用，如果产出是单一指标时OBTC 为1，MATC反映生产前沿面的平移，属于中性技术进步范畴。这种分解方式可以单独研究生产前沿面因为技术进步而发生的旋转效应。

3.收敛性模型。

利用新古典增长理论的收敛假说，分析沿黄流域城市土地利用全要素生产率指数的收敛性，常用的模型有绝对收敛和局部收敛，绝对收敛还可以再细分为σ收敛和绝对β收敛，局部收敛主要是条件β收敛。σ收敛反映的是各城市土地利用全要素生产率指数差异随时间变化的状况，通常用标准差和变异系数来检验，计算公式为：

其中，Yit表示第t年i城市的土地利用全要素生产率指数，-Yit表示t年n 个城市土地利用全要素生产率指数的均值，n是黄河流域城市总数。若CVt值随时间推移不断缩小，或者不同城市的离差随时间序列变化而下降，则认为满足σ 收敛，表明各城市土地利用全要素生产率指数的离散程度逐步缩小。

绝对β收敛的公式为：

其中，T是评价期时间间隔，α、β分别为变量参数，ε 为随机误差项。绝对收敛主要测量观察变量与变量初期之间的相关关系，目的在于判断是否存在“追赶效应”。若β ＜0，且通过了显著性检验，认为存在绝对收敛，表明黄河流域土地利用全要素生产率指数低的城市对土地利用全要素生产率指数高的城市具有“追赶效应”。

条件β收敛的公式为：

其中Xit为影响因素，m是条件影响因素的个数，γ是变量参数，其他变量如上描述。若β ＜0，且通过了显著性检验，认为存在条件收敛，表明黄河流域各城市土地全要素生产率指数值收敛于自身的稳定状态。

（三）指标构建与数据来源。

本文以黄河流域69个城市作为研究对象，且全文中所指“城市”界定都是其行政区划面积范围，因此，城市中的各地类划分，也遵照国家土地分类标准执行。

1.指标构建及说明。

根据古典经济学思想，城市土地利用全要素生产率指数的投入要素选取土地、资本和劳动力三类指标，产出要素选择期望产出（经济效益、社会效益）和非期望产出两类指标，环境变量选择常住人口、水域及水利设施用地面积两个指标，其对城市土地利用全要素生产率指数具有显著的影响并且属于短期内无法有效控制的外部变量，首先采用规模报酬不变条件下Super-SBM 模型得到各类投入指标的松弛量，接着消除环境变量的影响，最后采用调整后的指标计算城市土地利用全要素生产率指数。具体指标说明见表1所示。为了减少价格对指标的影响，利用GDP指数将各类价值指标平减到以2009年为基期的数值。

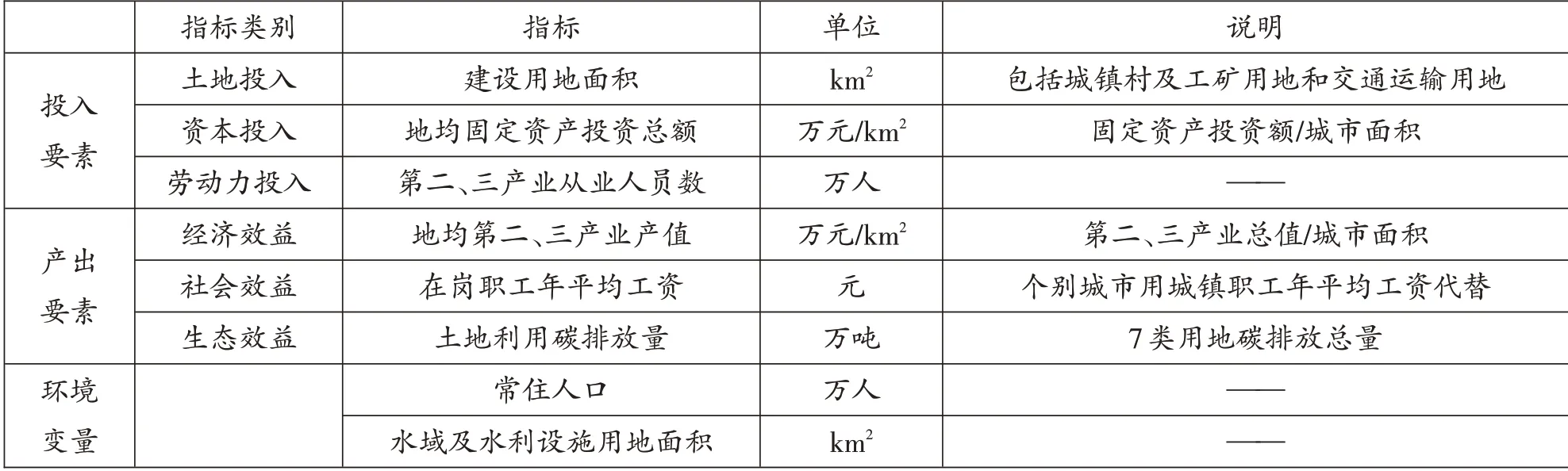
表1 城市土地利用全要素生产率指数测度指标

非期望产出指标——土地利用碳排放量的计算根据《2006年IPCC国家温室气体清单指南》中思想：“管理土地被用作借以确定人为源排放和汇清除的替代物”，划分为建设用地（能源消费）碳排放和其他地类碳排放两类，建设用地（能源消耗）碳排放选用各城市的能源消耗总量与每吨标准煤碳排放系数的乘积计入，其他地类碳排放主要计入耕地、园地、林地、草地、水域和其他未利用地。

其中，每吨标准煤的碳排放系数以赵荣钦、[15](p154-162)孙赫[16](p12-19)等学者对各类能源碳排放系数的计算结果作为参数值（表2），然后根据不同类型能源的占比作为权重计算各年综合碳排放系数（表3）。其他地类的碳排放系数选用孙贤斌等学者的研究结果（表2）。

从表2和表3计算得到各年的能源消耗碳排放系数略有差异，但均值为0.74 吨/吨标准煤，将此系数作为研究期间内每吨标准煤碳排放系数，计算各年的建设用地（能源消耗）碳排放量。汇总7类土地利用的碳排放总量作为指数测算中的非期望产出。

表2 不同类型能源碳排放系数（单位：kg标准煤、t/hm2）

表3 不同类型能源各年占比（单位：%、kg标准煤）

2.数据来源。

所有变量以2009—2018年为研究时段，指数测度所需的投入、产出变量及环境变量数据均来源于Wind 数据库和EPS 数据库，以及《中国国土资源年鉴》和各城市土地利用变化数据（2009—2018）等，部分缺失数据查看政府报告或者使用插值法补入。收敛检验所需的控制变量数据来源于《中国城市统计年鉴》（2009—2018）。

三、结果分析

（一）土地利用全要素生产率指数测度及分解。

利用MaxDEA 软件估算黄河流域69 个城市的土地利用全要素生产率指数。模型设定为规模报酬不变，投入角度进行Windows—Malmquist 分析时，窗宽设置为10，偏移设置为0，即得到该城市在整个研究期间内的移动平均指数值，并采用公式（3）和（4）对指数进行分解，结果如图1所示。

图1 黄河流域城市土地利用全要素生产率指数及分解指数变化

总体看，黄河流域各城市土地利用全要素生产率变化指数均值为1.096＞1.0，年均增长幅度9.6%，说明研究区间内土地利用生产率处于增加态势，且观察各城市的平均MI 值，除甘孜藏族自治州是0.998以外，其他城市都大于1.0，属于土地利用生产率增长状态，即在样本研究期，在既定的投入产出下实现了最优的产出规模。观察效率变化指数和技术变化指数，发现效率变化指数拖累了土地利用全要素生产率指数的提高，其对总体生产率指数的贡献为负，而技术进步指数对土地利用全要素生产率指数的贡献为正（11.1%），说明黄河流域城市土地利用全要素生产率的增长主要源于技术进步的推动。

其次，黄河流域城市土地利用全要素增长率存在时期差异，MI指数2010—2014年呈现增长趋势，2015—2018年整体呈现下降趋势，效率变化指数在2010—2012年呈现“追赶效应”，随后出现波动下降趋势，但技术进步变化指数在研究区间内呈现波动上升，进一步说明研究区间内由于技术创新导致生产前沿面的整体前移，所以给定相同投入下，最优产出也会比前一年有所提高。

进一步分解技术进步指数，发现投入偏向型技术进步和产出偏向型技术进步虽呈现波动特征，但是其值绝大部分小于1，而中性技术进步/技术规模变化指数均大于1，说明在研究区间内，生产前沿面向外发生了平移，技术进步主要因为技术规模变化导致，或者说技术规模变化的贡献要大于投入偏向型技术进步和产出偏向型技术进步，而且投入偏向型技术进步和产出偏向型技术进步的贡献为负。

（二）土地利用偏向型技术进步分析。

借鉴Barros 和Weber 提出的判定方法，[17](p642-653)充分利用2009—2018年黄河流域城市土地利用技术进步偏向型指数，结合各类投入产出的跨期比例，判断出技术进步的具体要素偏向，并分析投入和产出偏向型技术进步的演化特征。

首先，分析三种投入要素，包括建设用地面积、地均固定资产投资总额和第二三产业从业人员数。现在分别利用建设用地面积/地均固定资产投融资总额、建设用地面积/第二三产业从业人员数进行两两对比分析，发现在整个研究区间内，IBTC偏向于使用建设用地、节约资本的城市有44个，其中渭南、固原、新乡在研究期间8年处于这种投入方式，这或许由于建设用地是资源开发利用的基础，且这些城市的行政区划面积相对较大，所以在投资较短缺时，首先想到的是投入土地增加生产率的方式。IBTC偏向于使用建设用地、节约劳动力投入的城市也有44个，其中典型代表城市有：白银、定西、固原、商洛、济源、焦作，这是由于这些地区劳动力流出较多，因此为了获得更高土地利用生产率依然采用投入建设用地的方式。

按照研究区间内平均值分析，IBTC偏向于使用劳动力、节约建设用地的城市比例36.23%，偏向于使用固定资产投资，节约建设用地的城市比例也是36.23%，但这些城市并不全部重叠。从IBTC 偏向型的时间分布情况看，沿黄流域各时期采用投入资本节约建设用地方式的城市平均不足29 个。采用投入劳动力节约建设用地方式的城市平均不足36个。说明研究区间内大部分城市提高土地利用生产率仍旧依靠增加建设用地面积投入方式。各年使用固定资产投资、节约建设用地投入的城市数量随时间呈现波动上升的态势，2018年有32 个城市依旧采用这种方式提高土地利用生产率。

其次，分析三种产出要素，其中包含两种期望产出（地均第二三产业产值、职工年平均工资）和一种非期望产出（土地利用碳排放）。现分别将非期望产出与两种期望产出进行比较分析，可以发现，研究时期内OBTC 偏向增加地均第二三产业产值、减少碳排放量的城市有23个，典型代表城市有：阿坝、陇南、淄博和东营；OBTC 偏向增加职工年平均工资、减少碳排放量的城市有27个，典型代表城市是鄂尔多斯、海北、阿坝、甘孜、淄博和东营等。说明这些城市在研究区间里重视经济效益的同时不忘环境效益，提高土地利用生产率不以牺牲环境为代价。OBTC 偏向增加碳排放量、减少地均第二三产业产值或职工平均工资的城市比例66.67%，这些城市需要政府积极引导改变目前的投资结构，重视生态环境保护，努力实现环境效益、经济效益和社会效益多赢。

表4 是不同时期技术偏向性比重，可以发现黄河流域各城市不同时期主要以增加建设用地投入作为提升土地利用生产率的主要方式，其次是投入劳动力，最后才是投入资本。而从产出看，首先是以增加地均二、三产业产值为主，其次是增加职工年均工资，最后是增加碳排放量。这说明黄河流域在土地利用过程中，增加建设用地投入是主要方式，而碳排放量增加依旧是制约其生产率提升的主要因素，因此重视土地利用生态效益是目前沿黄流域的重要工作，这也是十八大以后政府工作新目标的导向。

表4 不同时期技术进步的偏向性比重

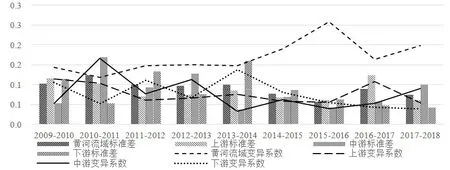
图2 黄河流域及其上、中、下游各年土地利用全要素生产变化指数的σ 收敛性

（三）土地利用全要素生产率指数收敛性分析。

1.σ 收敛分析。

基于Windows-Malmquist 模型的黄河流域土地利用全要素生产率指数计算其σ收敛性。可以发现随着时间的推进，整个黄河流域土地利用全要素生产率指数变异系数没有减小的趋势，但黄河流域上游城市与下游城市内部的土地利用全要素生产率指数变异系数具有趋小态势，黄河流域中游城市在2010—2013年内土地利用全要素生产率指数变异系数存在下降趋势，说明上游和下游各城市的土地利用生产率指数满足σ 收敛特性，而中游城市在2010—2013年里存在离散程度逐步缩小的态势。

2.β收敛分析。

利用公式（7）对69个城市的土地利用生产率指数进行绝对β收敛分析（表5）。可以看出，绝对β收敛检验中，各评价区域的土地利用全要素生产率指数都通过了t检验，黄河流域及其上、下游的土地利用全要素生产率指数在1%的水平上显著，中游则均在5%水平上显著，且β系数都＜0，表明黄河流域及其上、中、下游的土地利用全要素生产率指数具有绝对β收敛特征，如果没有外在干扰，各区域的土地利用全要素生产率指数收敛于各自的稳态，而且城市之间的土地利用全要素生产率指数具有“追赶效应”。条件β收敛检验中，引入城镇化率、人均GDP和建设用地占比三个指标作为控制变量，分别反映社会、经济和土地结构对促进土地利用生产率指数收敛的作用，利用公式（8）选择时间个体双向固定效应模型进行检验。可以发现，增加了控制变量条件以后，所有研究区域的土地利用全要素生产率指数值也都通过了t 检验，且回归系数均为负值，而且条件收敛的β系数普遍小于绝对收敛的β系数，上、下游内城市平均收敛速度＞中游内城市平均收敛速度，同一研究区域内条件β收敛下的平均收敛速度大于绝对β收敛下的平均收敛速度，体现了模型的收敛性减弱。从系数值分析，当黄河流域全域的土地利用生产率指数增加1%时，条件收敛下ln（TFPi+1/TFPi）减少1.121%，绝对收敛下ln（TFPi+1/TFPi）减少1.123%。观察控制变量的影响效果，可以发现，建设用地占比对城市土地利用全要素生产率指数的影响存在区域差异性，上、下游内建设用地占比显著正向影响，但全域内则显著负向影响；中游城镇化水平对城市土地利用全要素生产率指数具有正向弹性。

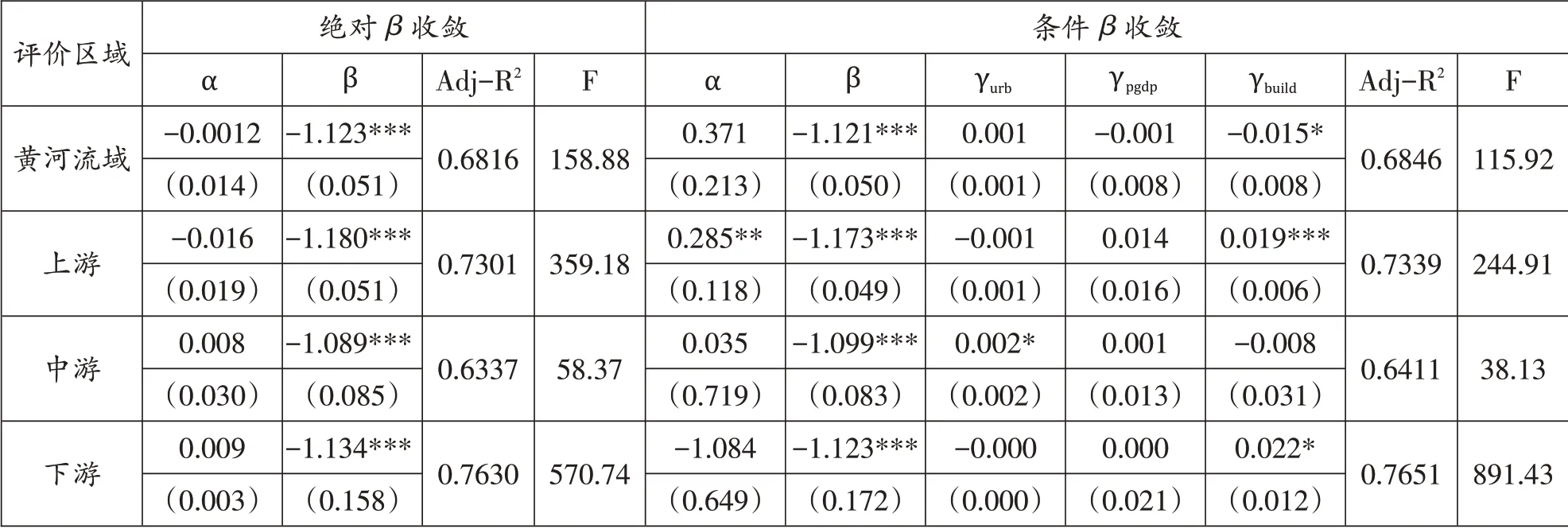
表5 评价期间土地利用全要素生产率指数的[β]收敛检验结果

四、结论与建议

本文结合方向距离函数Super-SBM 模型和Window-Malmquist 指数模型测算了黄河流域69 个城市土地利用全要素生产率变化指数并进行分解，从投入和产出两个角度判断技术进步的要素偏向性，并分析指数的收敛性和区域差异性，主要结论如下：

（一）自2011年以后，黄河流域城市土地利用全要素生产率指数均大于1，表明流域内城市土地利用生产率整体处于增长趋势，且土地利用全要素生产率的增长主要源于技术进步的推动，分解指数后发现技术进步指数对土地利用全要素生产率指数的贡献为正，投入偏向型技术进步和产出偏向型技术进步的贡献均为负。

（二）从投入偏向要素分析，流域内63.8%城市偏向于使用建设用地，从产出偏向要素分析，流域内偏向于减少非期望产出的城市仅23个，说明黄河流域的土地利用生产率还主要依靠投入土地资源，而产出方面则主要关注经济效益和社会效益，对生态效益关注不多。因此，建议黄河流域各城市要积极培训高层次人才，积极引导依靠劳力和资本促进城市土地利用的高效发展。国家在流域内各省积极实施生态保护政策，但是受经济发展影响，很多城市在土地利用建设过程中没有重视生态效益，因而效果受限，今后，各城市政府可以将国家生态保护政策与当地的经济效益和社会效益协同发展，真正做到黄河流域城市土地利用的高质量发展。

（三）从收敛性分析，黄河流域城市土地利用生产率指数在上游和下游具有σ收敛性，整个流域内和中游则不具有σ收敛性，但是四个区域内都存在绝对β收敛和条件β收敛，说明黄河流域土地利用生产率低的城市对土地利用生产率高的城市具有“追赶效应”，而且随着时间的推移各城市的土地利用生产率会收敛于各自的稳态，而且，条件收敛回归中，建设用地占比显著负向影响城市土地利用生产率指数的提高。因此，黄河流域内各城市在土地利用过程中，可以打破地域界限，加强交流与学习，积极鼓励创新技术与环境友好型技术的推广和应用，同时，还要考虑各地区的土地资源禀赋以及产业发展、城镇建设水平，提高土地利用稳态发展水平。