冷却时间约束多对多任务分配及其优化
刘冬宁,郑楚楚
(广东工业大学 计算机学院,广东省 广州市 510006)
社会高度信息化加快经济发展的同时,公共资源缺乏的现象也随之出现[1-7]。由于疫情原因,医院急诊和发热门诊的患者增多导致医院原始排班系统无法满足患者就诊。因此,在周期内合理分配有限数量的医生,有效地优化出诊系统,完善分配方案至关重要。
冷却时间作为时空约束常见的约束之一,冷却时间约束是指在一段连续工作的时间内,由于执行者(人或者设备)各方面的原因(体能,维护等)需要停止(休息)一段时间后,才能继续连续工作(如图1所示)。若不能有效地解决冷却时间约束,执行者的工作效率将事倍功半。前人在研究时空约束常用算法为搜索算法、基数模型、启发式或分布式等方法得到解决方案[8-10],得到的结果一般为局部最优结果,或部分研究成果为全局最优结果,但是求解的响应时间较长。
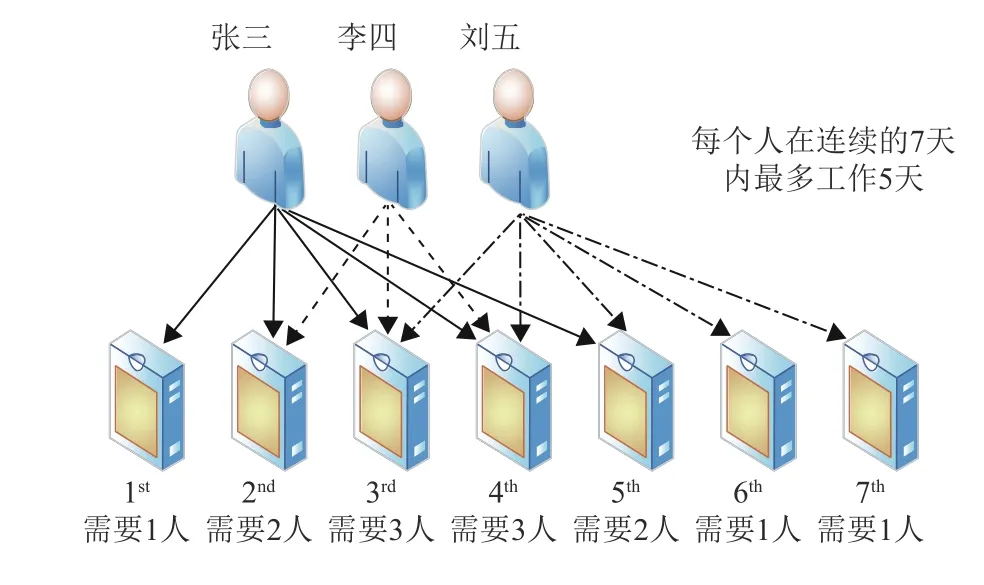
图1 冷却时间约束图Fig.1 Time sharing spatiotemporal constraint graph
针对此,本文以医院排班为案例,提出解决冷却时间约束多对多任务分配的形式化模型,该模型主要基于群组角色多对多指派模型(Group Multirole Assignment,简称GMRA)[11-18]。基于该模型,可将问题采用整数规划的形式化表达,并利用IBM优化包CPLEX[19]以秒分级的效率得到解决方案。
论文结构如下:第1节提出一个实际问题。第2节将第1节中的实际问题利用GMRA和E-CARGO模型进行形式化描述,并建立模型。实验结果分析与必要条件的证明在第3节,并通过规模性实验验证了必要条件的可靠性。第4节本文的结论。
1 场景预设
B医院急诊科需要根据以往急诊科医生出诊的情况对9名医生进行出诊排班,9名急诊科医生对每天出诊的意愿是不同的,这取决于医生出诊的心态和医生是否愿意当天出诊。医院的吴人事主管根据7天急诊科需要出诊医生的数量对9名医生进行排班,其中每天具体需要几名医生如表1所示。吴主管根据以往9名医生出诊概率的情况(如表2所示)需要对9名医生进行出诊排班。为了保证医生出诊的效率以及病患得到高效的医治,医院规定每名医生在连续的7天内必须休息2天(可以非连续的两天)以保证医生出诊的效率。因此,急诊科9名医生在排班过程中受冷却时间约束的限制(连续7天的工作周期内必须休息两天)。

表1 任务需求表Table 1 Task requirement table
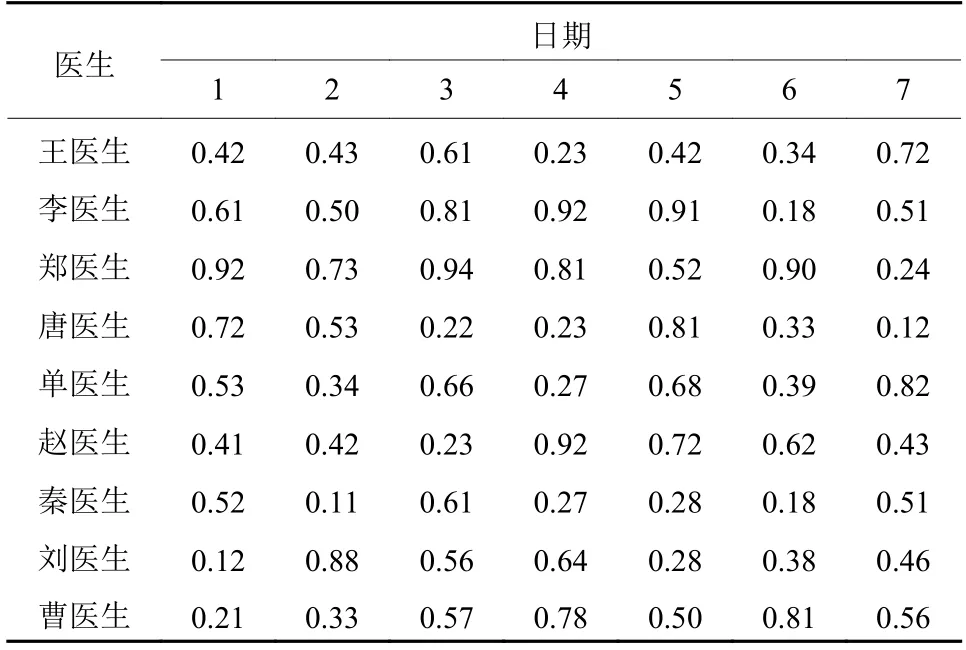
表2 医生出诊概率矩阵Table 2 Doctor visiting probability matrix
吴主管现在面临的主要问题是,如何安排9名医生完成周期为7天的出诊任务,并且符合医院的规定,以及根据表2的评估矩阵得到医生出诊的最优指派。
因此,本文采用了GMRA模型对冷却时间约束下的急诊科出诊排班予以解决。
2 数学模型
GMRA模型是基于角色协同理论(Role-Based Collaboration,简称RBC)[10-11]及其通用模型ECARGO的。E-CARGO模型的形式化表达为:它将协作系统的组件表示为一个9元组∑::=
在讨论角色分配问题[8-9]时,环境(E)和群(G)分别被简化为向量和矩阵。此外,使用非负整数m(=|A|,其中|A|是集合A的基数)来表示代理集A的大小,n(=|R|)角色集的大小R,i,i1,i2, ···代理的索引,以及j,j1,j2, ···角色的索引。
因此,基于E-CARGO通用模型及其子模型GMRA,可将冷却时间约束多对多指派问题形式化如下:
定义1 属性集Ⓢ。属性集是一组定义为对象的属性集,该对象由P0,P1,P2···Pl-1标识,其中l=|Ⓢ|。
注意:在场景中,Ⓢ={“医生出诊的状态”,“医生出诊的喜好”}。下面定义5中提到的矩阵Q的元素高度依赖于集合Ⓢ。
定义2 角色,角色被定义为r:: =
例如:上述场景中有条记录为2nd=<“2”,7>其中“2”表示第3天(记录从0开始)需要7名医生出诊(本文通过E-CARGO模型将每天视为角色)。
定义3 代理,代理根据E-CARGO被定义为a::=
例如,在场景中,可能有一个记录:王医生=<“001”,{ 0.42,0.43,0.61,0.23,0.42,0.34,0.72}>。王医生的内部id是“001”。值0.42表示王医生以往第1天出诊的概率(包含医生出诊时对病人就诊的效率)。角色相当于请求,代理被视为资源。可将时间(天)形式化为角色,将每名医生形式化为代理。
定义4 角色需求向量L是群组g中环境e的角色范围下界的向量。
例如:在上述场景中,L反映的是总共需要多少名医生。其中L[j]为常数,如L[6]=7,表示第7天需要7名医生(j的计数单位是从0开始)。因此,在本文中也称L为需求向量。
定义5 评估矩阵Q是m×n的矩阵,其中Q[i,j]∈[0,1]表示代理i∈N(0≤i<m)对角色j∈N(0≤j<n)的评估值。Q[i,j]=0表示最小值,1表示最高值。
例如,在分配代理的过程中,代理需要根据Ⓡ中的所有元素进行比较得到一个公平值,通过2维矩阵的形式得到一个Q矩阵。本文假设Q[i,j]的值已经确定,并且是每名医生对以往每天出诊的意愿(如以往的星期一医生是否愿意出诊)。本文中的一组假设实验值见表2。
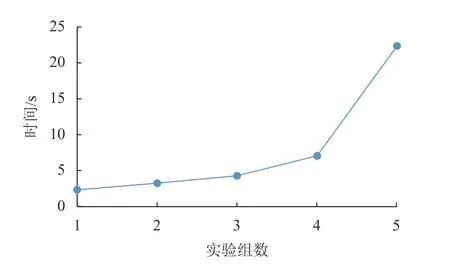
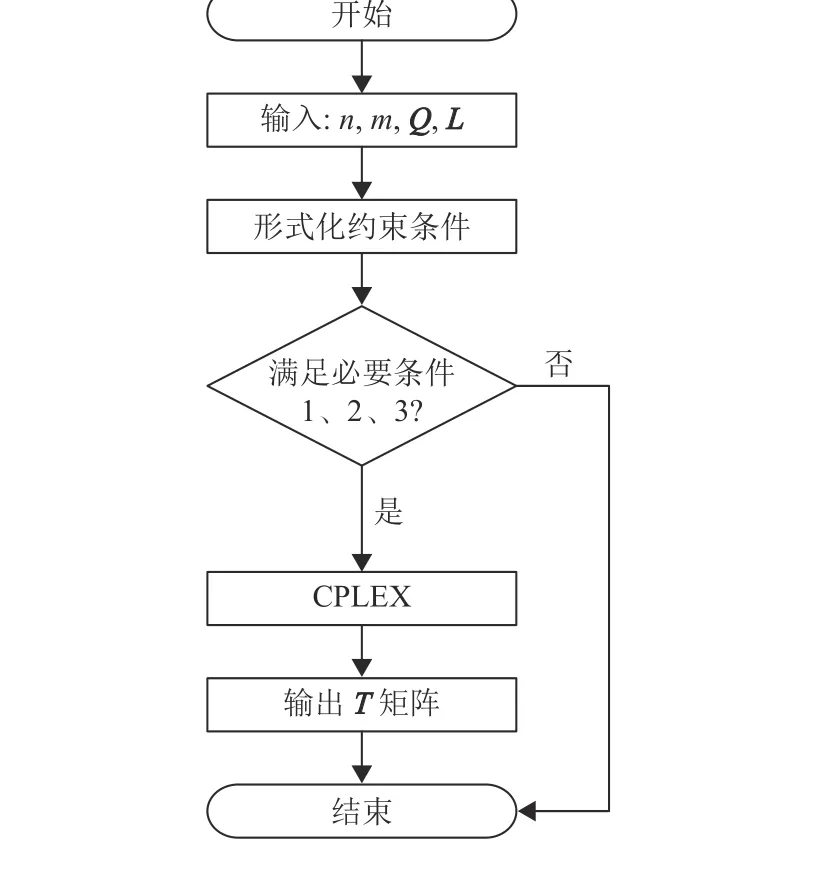
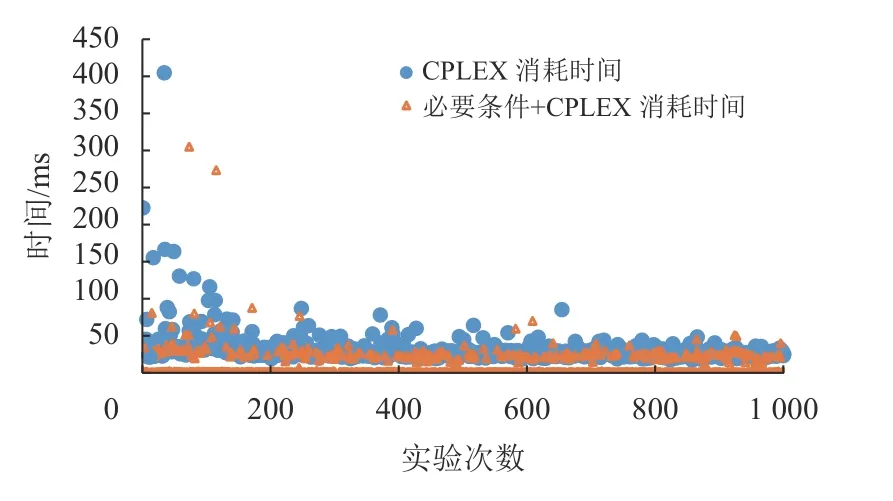
定义6 代理能力值向量La表示最多可分配给代理的角色数,即La[i](0≤i 例如:代理可以分配的最大角色数(天)取决于总角色数(工作周期)。例如,对于本文场景预设中所提到的场景中,代理能力值为La[i]=5。 定义7 角色分配矩阵T定义为m×n矩阵,其中T[i,j]∈{0,1}表示代理i是否被分配给角色j,T[i,j]=1表示是,反之T[i,j]=0表示否。 根据上述定义,在多对多指派中群组g可以由Q、L、La和T表示。 定义11 已知代理数量m,角色数量n,评估矩阵Q,需求向量L,代理能力值向量La,则需要为多对多指派寻求一个可行的分配矩阵T且效益最高,即 其中,表达式(1)为0-1约束,其中0表示代理i未分配,1表示代理i所扮演的角色为j;式(2)使群组g有可行解,每个角色都有足够的代理扮演;式(3)表示每个代理最多只能分配给有限数量的角色;式(4)表示每个代理在7天的周期内最多可以工作5天。 在描述本文问题时,可将每天视为角色,每名医生视为代理。Q[i,j](0≤i 本文采用GMRA理论和E-CARGO模型将冷却时间约束以及多对多指派问题形式化表达,从而简化了冷却时间约束下的多对多指派建模与求解,实验结果分析如下。 实验配置如表3所示。 表3 实验配置Table 3 Experiment configurations 本文解决冷却时间约束下多对多指派的步骤为:步骤1:确定代理数量(m),角色数量(n),角色需求量(L)。 步骤2:根据GMRA理论和E-CARGO模型将冷却时间约束形式化表达。 步骤3:利用IBM 优化包CPLEX进行计算。 步骤4:得到最优解和解决方案或无法指派。 在第1节所提到的实际场景中医院急诊科医生出诊的排班,本文根据上述步骤得到的解决方案如图2所示。 图2 分配矩阵Fig.2 Distribution matrix 图2中每行表示一名医生出诊的状态,每列表示出诊的日期,1表示医生分配出诊,每行的总和表示某名医生在7天内一共出诊天数,0表示医生休息,每列的总和表示每天一共出诊医生的数量。实验结果的总体效率值为25.43。 根据实际情况,医院需要医生尽可能出诊,从而减轻患者等待时间。因此,医院会有临时增加医生出诊的需求,同时必须考虑到突发事件。本文为解决此问题,在数量和排班日期不变条件下,增加了医生的需求量,保证解决方案的有效性。 其中实验变化的数据为每天平均增加1名医生出诊,实验结果方案如图3所示。 图3 增加需求分配矩阵Fig.3 Add demand allocation matrix 图3中所得到的团队效益为27.2,从图中可发现,这9名医生已经处于工作饱和状态,其中还能增加出诊的医生分别为刘医生和秦医生,并且这两名医生最多只能增加2天出诊,由于冷却时间约束,限制了两名医生出诊的日期。 冷却时间约束多对多指派问题随着角色数量和代理数量增加,时间复杂度将会变高,因此,本文针对时间复杂度的问题完成了规模性实验,其中实验分为5组,每组实验包含100种情况,第1组代理数量m=9,角色数量n=7,需求向量L=[1,m];第2组代理数量m=15,角色数量n=15需求向量L=[1,m];第3组代理数量m=20,角色数量n=20需求向量L=[1,m];第4组代理数量m=30,角色数量n=35,需求向量L=[1,m];第5组代理数量m=40,角色数量n=40,需求向量L=[1,m]。时间对比如图4所示。 图4 CPLEX规模性实验时间分析Fig.4 Time analysis of large scale experiment 图4反映了实验随着规模增大,实验的复杂度成指数性变化。规模增大时,实验速度将成为重要的问题。因此,需要找到一个合理的加速条件,筛选出无解的情况,从而保证实验的速度。同时,现实生活中存在突发情况,如疫情发生时,需要更多的医生出诊,排班时间也将从天变为小时或者分钟计算。医院的排班系统随时可能发生变化,为了应对突发情况决策者必须考虑时间复杂度的问题。 医院排班系统常常遇到紧急情况,医生的排班随时需要调整。因此,在保证解决方案可行时,还需要考虑如何优化系统提高实验的效率。 针对实验加速的问题进一步形式化描述,并增加符号及下标如下: (1) 求和函数sum(),sum(L)表示一共有多个角色需要扮演。 (2) sum(T[i])表示第i个代理一共指派给多少个角色。 (3) 一个周期长度为U。例如在一段连续的时间内,其中每7天为一个周期,那么U=7。 (4) 一个周期U内最多工作时长为p,其中p≤U。例如一个周期为7天的工作时长,最多工作5天。那么p= 5。 引理1(必要条件1) 每个时段的角色数量不能超过总代理数量(|A|)。 引理2(代理最大工作时长) 在一个工作周期为n的时长内,任意为7的时间内代理工作时长不能超过5,则在工作周期为n,代理工作时长最大取值为n除以7向下取整记为a,得到的余数c若小于等于5,则p=5a+c, 若余数大于5,则p=5a+5。 定理1(必要条件2) 冷却时间约束的整体任务下,所有代理最多扮演的角色数量不能小于sum(L)。 证明 假设有m个代理,每个代理最多工作时长为p,那么m个代理最多可以扮演的角色数量为m×p。那么要生成一个分配矩阵T必须有以下关系即 则无法出现指派结果,因此要想存在一个合理的指派方案必须有sum(L)≤m×p的成立。 定理2(必要条件3) 每组代理在相邻工作周期U中最长工作时间不能超过p。公式为 证明 周期为U的时间段内,当存在一个j使代理工作时长大于p,那么此情况一定不会存在一个合理的分配矩阵T。 为了验证解决方案的有效性,本文采用随机的方式做出对比,实验数据以及实验对比分别为,排班天数为10天,代理的数量为20名医生。医院中医生的Q矩阵是随机产生,保证实验的随机性。其中实验流程图如图5所示。 图5 必要条件流程图Fig.5 Necessary conditions flow chart 通过10000组对比实验验证必要条件的加速效果,其中实验的取值范围为需求向量L随机取值的范围变化分别为:L∈[1,20],L∈[3,20],L∈[5,20],L∈[9,20],L∈[1,25]。得到以下数据:CPLEX中有890组数据无解,必要条件同样找到890组数据无解,并且两者找到的数据是一致的。表4所示为10000组实验,必要条件对比于CPLEX效率提升表。本文从中随机筛选出1000组数据对比时间的变化如图6所示。 表4 必要条件效率提升表Table 4 Necessary condition efficiency improvement table 在上述的规模性实验中,5组的无解比例分别为:8.7%,14.8%,38.8%,74.9%,89%。并且CPLEX与必要条件筛选出来的数据是一致的。从图6分析发现必要条件筛选出大量无解的情况,确实有助于加速实验,保证速度提升的同时,也保证了解决方案的的准确性。 图6 必要条件与CPLEX时间对比Fig.6 CPLEX and necessary condition 表4为必要条件的实验效率表,必要条件总体效率提高了40.74%,可能有个别情况无法提升实验速度,但是总体提升效率很高。此套程序适用于紧急事件。例如疫情的发生,医务人员可能是以小时为单位进行排班,医院在排班过程中必须考虑医生的休息情况以及体能状态,以保证医生出诊的效率。对于此类紧急事件,医院必须缩小排班消耗的时间并且保证得到的效果是最优指派,使得更多病患得到有效的医治。 本文研究冷却时间约束下多对多任务分配及其优化的问题,使用GMRA模型对该类问题进行了形式化建模和求解。首先分析冷却时间约束耦合问题,针对冷却时间约束采用线性规划的方式建立约束之间的关系,继而建立了冷却时间约束多对多任务指派模型,形式化冷却时间约束证明了该问题的必要条件,并通过消除无解的情况对解空间进行归约。该模型的求解是基于整数线性规划的模型,借助 CPLEX生成解决方案,在秒分级时间范围内,满足了冷却时间约束多对多指派快速响应的需求。最后,本文对冷却时间约束下的多对多任务分配进行了大规模仿真实验,实验结果验证了本文所提出的模型和方法具有时效性,适用于一般的冷却时间约束多对多指派问题,并通过必要条件对解空间的快速归约,使得实验平均加速为40.74%左右。在下一步工作中,可沿以下思路进一步完善研究: (1) 采用GMRA方法解决其他更多的时空约束下的任务及资源分配问题; (2) 进一步证明冷却时间约束的充分必要条件及相关对应定理等问题。
3 实验分析及结果
3.1 问题求解与实验分析



3.2 优化实验

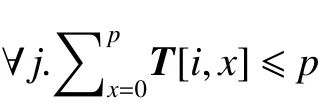

4 结论

