Passivity-Based Robust Control Against Quantified False Data Injection Attacks in Cyber-Physical Systems
Yue Zhao, Ze Chen, Chunjie Zhou, Yu-Chu Tian,, and Yuanqing Qin
Abstract—Secure control against cyber attacks becomes increasingly significant in cyber-physical systems (CPSs). False data injection attacks are a class of cyber attacks that aim to compromise CPS functions by injecting false data such as sensor measurements and control signals. For quantified false data injection attacks, this paper establishes an effective defense framework from the energy conversion perspective. Then, we design an energy controller to dynamically adjust the system energy changes caused by unknown attacks. The designed energy controller stabilizes the attacked CPSs and ensures the dynamic performance of the system by adjusting the amount of damping injection. Moreover, with the L2disturbance attenuation technique,theburdenof control systemdesignissimplified because there is no need to design an attack observer. In addition,this secure control method is simple to implement because it avoids complicated mathematical operations. The effectiveness of our control method is demonstrated through an industrial CPS that controls a permanent magnet synchronous motor.
I. INTRODUCTION
RECENTLY, cyber attacks against cyber-physical systems(CPSs) have increasingly occured. Due to the existence of such attacks, CPSs usually exhibit strong nonlinear characteristics. The inherent nonlinear nature of the attacked CPSs has motivated the research of nonlinear control methods in security control. Existing investigations have delved into the nonlinear control of CPSs include adaptive control [1], [2],sliding mode control [3] and model predictive control [4]–[6].
Existing nonlinear control methods against cyber attacks have been studied mostly from the perspective of signal processing. These nonlinear control methods show some disadvantages. For example, the design of adaptive control methods is usually complicated. When the control system has non-parametric uncertainties, its robustness is greatly affected by model errors. As another example, the application of sliding mode control methods not only shows a chattering phenomenon, but also is restricted by the relative order of the system. Furthermore, the backstepping control method is easy to cause the dimensional expansion of the system. The model predictive control method demands a large amount of calculation. As a result, the control time is difficult to guarantee. Because attacks are unpredictable, time-varying,and complex, these high-gain control methods have limited ability to deal with attacks.
The design of adaptive secure controller in [7] counteracts denial-of-service (DoS) attacks as well as external disturbances. They offset the impact of unknown attacks on the system in real time. However, the selection of adaptive parameters is a difficult task as attacks are changeable. The study reported in [8] uses an backstepping secure controller to deal with attacks. However, this controller is only designed for second-order systems. Its applications to high-order systems are difficult because it will cause dimensional expansion problems. The work in [9] investigates discretetime cyber-physical systems under actuator and sensor attacks.As attacks are unknown, it adopts an observer-based control scheme to stabilize attacked systems. But the design of the additional attack observer complicates control system design.The reports in [10]–[13] consider a model predictive control algorithms to handle attacks for discrete-time systems. They solve an optimization problem with some constraints expressed by linear matrix inequalities. However, the optimization process is computationally expensive, increasing the complexity of the control problem.
In the fields of science and engineering, it is generally believed that the change in various physical quantities in dynamic systems reflect a change in energy (absorption,conversion, and consumption). For example, the change in current flowing through an inductor reflects the change in magnetic field energy. Therefore, the physical quantity of the system can be controlled through the control of the system energy. The passivity of the system is the energy change property of the system. Passivity-based control [14]–[16] is an inherently nonlinear control method because of its good physical interpretation and global convergence characteristics.With an intuitive physical concept, this nonlinear control method provides a physical explanation for control behavior[17], [18]. It not only ensures the stability of the system but also improves the dynamic performance of the system through the method of damping injection [19]–[21]. Compared with other nonlinear control methods based on signal processing,the passive-based control method does not need to solve the high-gain feedback control law. Thus, it is computationally simpler, implying that it is easier to implement in engineering.
However, a CPS under passivity-based control has weak stability when it is attacked. When false data injection attacks[22], [23] occur, the control commands and/or sensor outputs are maliciously increased or reduced. Eventually, the system energy will be maliciously changed, causing system instability. There are two main ways to increase the stability of the system: 1) Use the observer [24], [25] to observe, and compensate for, the attack, and 2) Use theL2disturbance attenuation method [26], [27] to suppress the impact of the attack on the system to a certain level. Due to the unpredictability of attacks, the existing disturbance observer may fail when observing unknown attacks. The design of the attack observer will increase the cost and difficulty of the control system design. Therefore, this paper combines the Hamiltonian system theory and theL2disturbance attenuation control technology. Adopting the passivity-based method of interconnection and damping configuration, we design a passivity-based robust controller from the port controlled Hamiltonian with dissipation (PCHD) model to improve the control quality.
Overall, this paper makes the following two main contributions to the security of CPSs under false data injection attacks:
1) A defense framework is proposed from the perspective of energy conversion; and
2) With theL2gain disturbance attenuation technology, a passivity-based robust controller from the port controlled Hamiltonian model is designed to stabilize the attacked CPSs.
The remainder of this paper is organized as follows:Section II describes our defense framework based on energy conversion. This is followed by our deign of a passivity-based robust controller in Section III. Section IV gives experimental results. Finally, Section V concludes the paper.
Notations:R , Rn, and Rm×nstand for real space,ndimensional real space, andm×nreal matrices, respectively.||·|| means the 1-norm of a vector or matrix.Imrepresents anm-order unit matrix. diag(x1,...,xm) denotes a diagonal matrix.ATmeans the transpose of a vector or matrixA.
II. DEFENSE FRAMEwORk BASED ON ENERGY CONVERSION
In this section, we describe a defense framework from the perspective of energy conversion. The framework is based on system transformation.
A. System Model Conversion for Energy Control
For an arbitraryn- inputn-output affine nonlinear system:

wherex∈Rnis a system state vector,u∈Rnrepresents control input vector,y∈Rndenotes sensor output vector,f(x)∈Rnandh(x)∈Rnare function vectors, andg(x)∈Rn×nis a function matrix.
Almost all existing studies carry out secure control from the perspective of signal processing, with their defense framework based on system (1). However, this article designs a defense framework from the perspective of energy conversion. For energy control, system (1) is transformed into the following port controlled Hamiltonian with passivity (PCHD) form:

B. Description of Attacks
Typical attacks include denial-of-service attacks [28], [29],false data injection attacks [30], [31] replay attacks [32], [33],zero-dynamic attacks [34], and covert attacks [35], [36]. The false data injection attacks are simple to implement and can arbitrarily destroy a system. Therefore, there are many related literatures researching security control issues under false data injection attacks, such as in [37]–[39].
The false data injection attack models in the literature are usually complicated because intelligent attackers are usually in conjunction with system models. Therefore, the attackers need to adopt system identification methods [40]–[42] to obtain the system model. This process is very complicated,which limits the application of these attack models. In addition, no matter how smart the attack models are, their ultimate effect on the system is reflected in the malicious change of control commands and/or sensor outputs.
Therefore, this article dispenses with the application of these complex false data injection attack models. It finds a new way of false data injection attacks to attribute the impact of the attack on the system to the malicious increase or decrease of control commands and/or sensor outputs. This new way of exploits is simple to design and easy to implement for increasing or reducing control commands and/or sensor outputs. Ultimately, it can purposefully compromise the system. The exploit strategies are shown as follows:


C. System Under Actuator and Sensor Attacks
When attacks and external disturbances occur, system (2) is transformed into

III. DESIGN OF PASSIVITY-BASED RObUST CONTROLLER
A. Energy Shaping and Damping Injection
In order to configure the energy of system (5), and construct the energy function of the closed-loop system, in this subsection, we assume that there is no uncertainty occur.Then, system (5) becomes

The interconnection and damping assignment passivity based control (IDA-PBC) method is used to feedback stabilize system (6). Then, the closed-loop system (6) becomes

B. Design of Passivity-Based Robust Controller
When attacks, disturbances, and conversion errors occur,system (6) becomes the form of system (5). Under feedback control lawu=α(x), system (6) can be stabilized in the neighborhood of equilibrium pointx*. However, when attacks occur, system (5) has weak stability under controlleru=α(x).Therefore, we design a passivity-based robust controller (14)to stabilize the attacked system (5).

Under controller (14), system (5) becomes
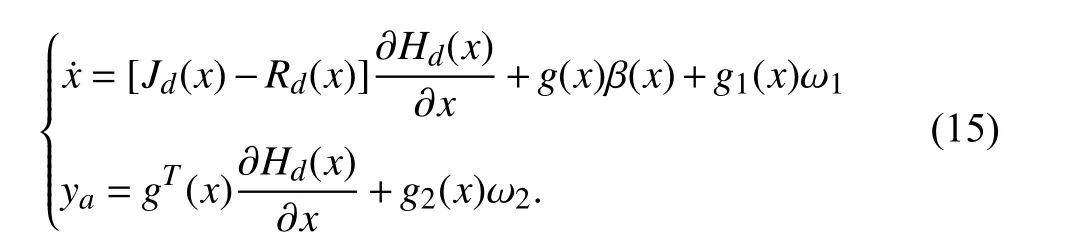
The next goal is to design the control law β(x) for system(15). For this purpose, the true or estimated values ofg1(x)ω1andg2(x)ω2need to be available. The fact is that these two uncertain terms are unknown. Thus, disturbance observers need to be designed to estimate their values. To simplify the control system design, this paper uses theL2disturbance attenuation technique to suppressg1(x)ω1andg2(x)ω2within a certain level. This idea has been used in the disturbance attenuation problem of nonlinear systems [43]–[45].
For system (15), define the penalty signal as

Proof:The proof of Theorem 2 is given in Appendix B. ■
Remark 2:Combining (12) and (18), controller (14)becomes the form of controller (19). Under controller (19),system (5) is stable in the presence of attacks.

Remark 3:The secure control method proposed in this paper has the following advantages:
1) It has a good physical interpretation and global convergence characteristics. Meanwhile, it avoids complicated mathematical operations. Moreover, as there is no need to design an attack observer, it simplifies the burden of control system design;
2) It drives the system states to converge to the origin by promptly adjusting the system energy changes in the presence of attacks; and
3) It ensures the dynamic performance of the system by adjusting the amount of damping injection.
IV. NUMERICAL SIMULATIONS
In this section, numerical simulations are conducted to demonstrate the performance of the proposed controller for CPSs under cyber attacks.
A. Descriptions of An Example
We consider a control system of an interior permanent magnet synchronous motor (IPMSM), as shown in Fig. 1. The controller proposed in this paper is applied to the current loop.

Fig. 1. A control system for a interior permanent magnet synchronous motor.

B. Design of Existing Controllers
When attacks and disturbances occur, system (21) is transformed into


When attacks and external disturbances occur, system (29)becomes

The parameters of controllers (23)–(25) and (42) are tabulated in Table I.

TABLE I PARAMETERS OF CONTROLLERS
D. Design of Thirteen Case Studies and Four Control Strategies
Thirteen cases are designed to validate the effectiveness of the proposed controller, as shown in Table II.
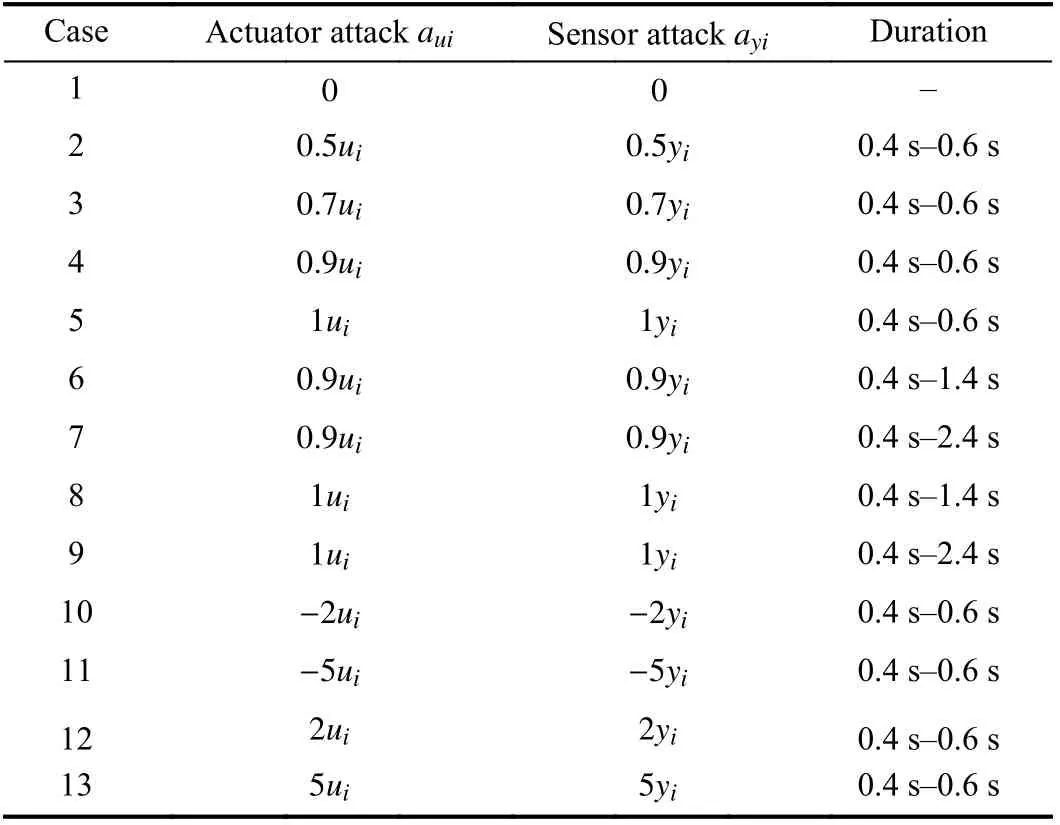
TABLEII TEN CASES OF ATTACkSaui AND ayi (i =1,2)
For comparative performance analysis, four control strategies are designed for system (20), as shown in Table III.Control strategies 1, 2, and 3 are existing control strategies.Control strategy 4 comes from our control strategy.
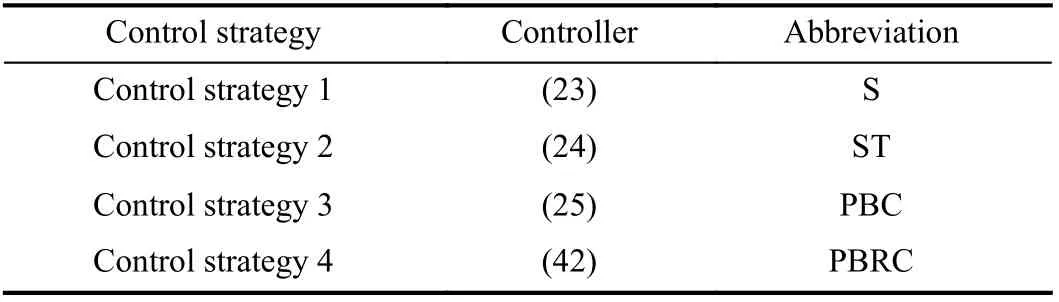
TABLE III FOUR CONTROL STRATEGIES
E. Five Case Studies With Positively Decreased ui and yi
In this subsection, numerical experiments are implemented when the control commandsuiand sensor outputsyiare decreased since actuator attackauiand sensor attackayiare increased reversely.
1) Case 1:In this case, no attack signal is implemented. The simulation results are shown in Fig. 2.
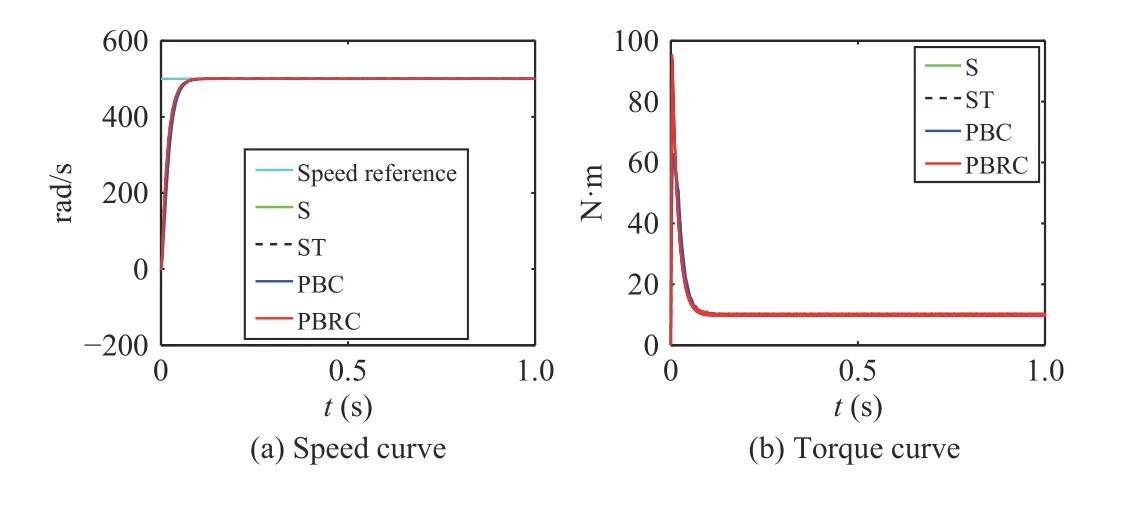
Fig. 2. Case 1 without attack (a ui=0, a yi=0, d =10 N·m).
2) Case 2:Both actuator commandsu1andu2, and sensor outputsy1andy2of system (20) are reduced by 5 0% between 0.4 s and 0.6 s. Our simulation results are shown in Fig. 3.

Fig. 3. Case 2 (a ui=-0.5 , a yi=-0.5, d =10 N·m, 0.4 s–0.6 s).
3) Case 3:Both actuator commandsu1andu2, and sensor outputsy1andy2of system (20) are reduced by 7 0% between 0.4 s and 0.6 s. The simulation results are depicted in Fig. 4.
4) Case 4:Both actuator commandsu1andu2, and sensor outputsy1andy2of system (20) are reduced by 9 0% between 0.4 s and 0.6 s. The results are illustrated in Fig. 5.
5) Case 5:Both actuator commandsu1andu2, and sensor outputsy1andy2of system (20) are reduced by 1 00% between 0.4 s and 0.6 s. The results are illustrated in Fig. 6.
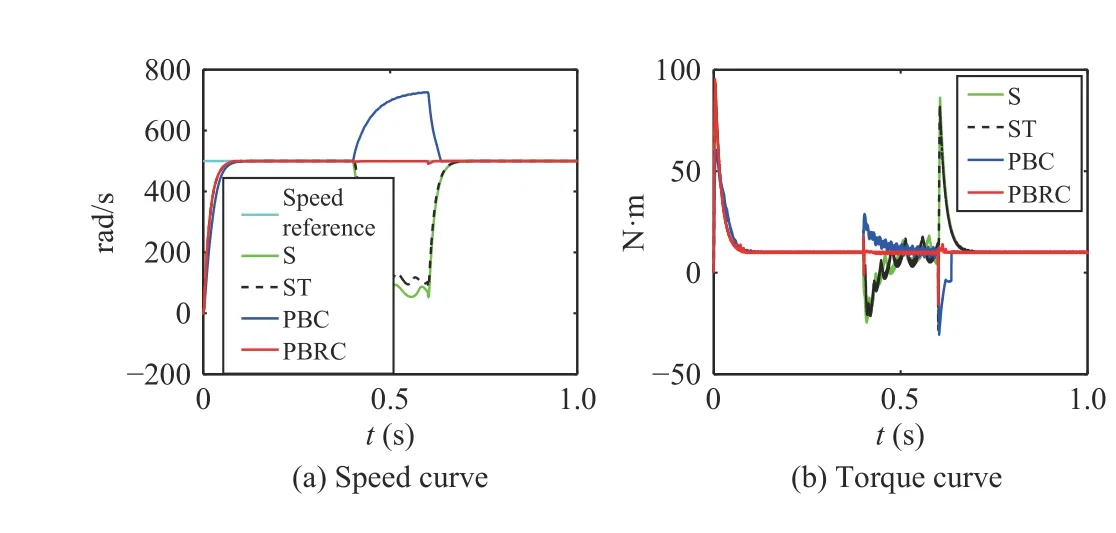
Fig. 4. Case 3 (a ui=-0.7 , a yi=-0.7, d =10 N·m, 0.4 s–0.6 s).
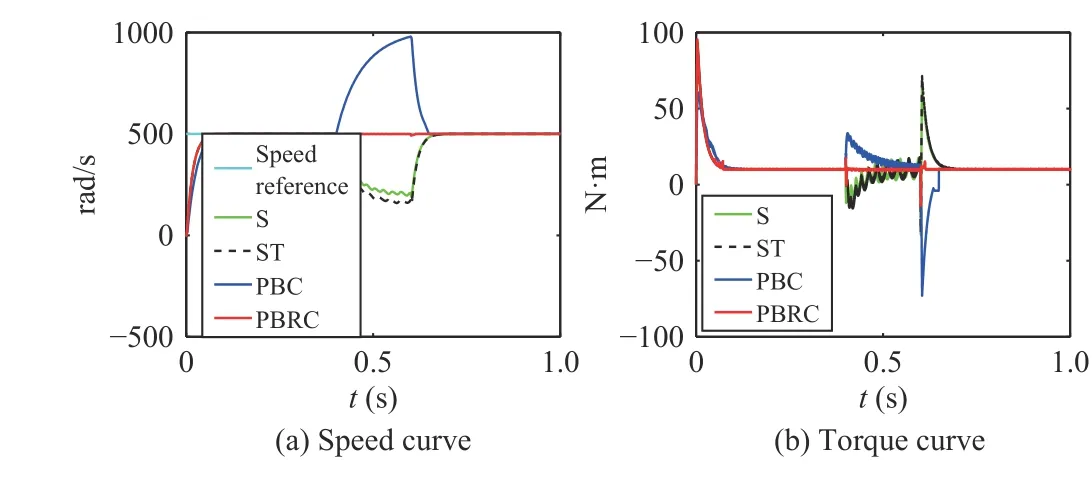
Fig. 5. Case 4 (a ui=-0.9 , a yi=-0.9, d =10 N·m, 0.4 s–0.6 s).

Fig. 6. Case 5 (a ui=-1, a yi=-1, d =10 N·m, 0.4 s–0.6 s).

Fig. 7. Case 6 (a ui=-0.9 , a yi=-0.9, d =10 N·m, 0.4 s–1.4 s).

Fig. 8. Case 7 (a ui=-0.9 , a yi=-0.9, d =10 N·m, 0.4 s–2.4 s).

Fig. 9. Case 8 (a ui=-1, a yi=-1, d =10 N·m, 0.4 s–1.4 s).
As shown in Figs. 2 and 3, when there is no attack or in face of a weak attack, the motor works well under all of the four controllers. Under Cases 3 and 5, Figs. 4–6 indicate that the control performance of controller (23), (24), and (25) has declined during 0.4 s to 0.6 s, however, our controller (42) can always work normally.
F. Four Case Studies With Different Values of Attack Duration
In this subsection, in contrast to Cases 4 and 5, some experiments are carried out under the same attack intensity but different attack duration.
1) Case 6:In this case,u1,u2,y1, andy2of system (20) are reduced by 9 0% between 0.4 s and 1.4 s. The simulation results are shown in Fig. 7.
2) Case 7:Both actuator commandsu1andu2, and sensor outputsy1andy2of system (20) are reduced by 90% between 0.4 s and 2.4 s. The simulation results are depicted in Fig. 8.
3) Case 8:In this case,u1,u2,y1, andy2of system (20) are reduced by 100% between 0.4 s and 1.4 s. The simulation results are shown in Fig. 9.
4) Case 9:Both actuator commandsu1andu2, and sensor outputsy1andy2of system (20) are reduced by 1 00% between 0.4 s and 2.4 s. The simulation results are depicted in Fig. 10.
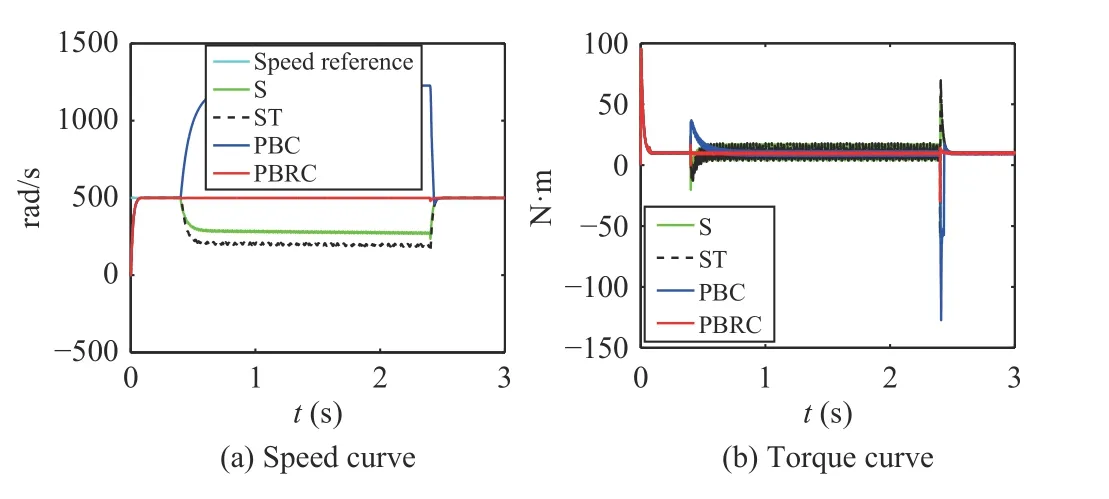
Fig. 10. Case 9 (a ui=-1, a yi=-1, d =10 N·m, 0.4 s–2.4 s).
For Cases 4–9, during the period that the system is attacked,Figs. 5–10 show that as the attack duration increases, the time when the control performance of controllers (23)–(25) are reduced has also been extended. However, our controller (42)still works well even if the attack duration is extended.
G. Two Case Studies With Reversely Increased ui andyi
As the attack intensityaui,ayicontinue to increase reversely, the direction of the control commandsuiand sensor outputsyiwill change from positive to negative. In this subsection, some experiments on this situation will be tested.
1) Case 10:In this case,u1,u2,y1, andy2of system (20) are reduced by 2 00% between 0.4 s and 0.6 s. The simulation results are shown in Fig. 11.
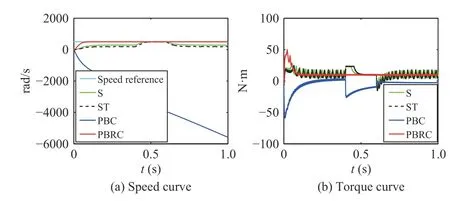
Fig. 11. Case 10 (a ui=-2 , a yi=-2, d =10 N·m, 0.4 s–0.6 s).
2) Case 11:Both actuator commandsu1andu2, and sensor outputsy1,y2of system (20) are reduced 500% between 0.4 s and 0.6 s. The simulation results are shown in Fig. 12.

Fig. 12. Case 11 (a ui=-5 , a yi=-5, d =10 N·m, 0.4 s–0.6 s).
Under Case 10, Fig. 11 shows that when control commands and sensor outputs are reversed, the control performance of controllers (23)–(25) has failed. On the contrary, our controller (42) is still resilient to attack. Under Case 11, Fig. 12 shows that when control commands and sensor outputs are more severely reversed, our controller has also failed.
H. Two Case Studies With Positively Increased ui and yi
In this subsection, some experiments are implemented on the situation where the control commandsuiand sensor outputsyiare increased since actuator attackauiand sensor attackayiare increased positively.
1) Case 12:Both actuator commandsu1andu2, and sensor outputsy1andy2of system (20) are increased 200% between 0.4 s and 0.6 s. The results are shown in Fig. 13.
2) Case 13:In this case, both actuator commandsu1andu2,and sensor outputsy1andy2of system (20) are increased 500%. The simulation results are shown in Fig. 14.
Under Cases 12 and 13, Figs. 13 and 14 show that when the control commands and sensor outputs are positively increased by attacker, the control performance of all of the four controllers can remain normally.
I. Verification of Our Method Under Different Speed References
In this subsection, some experiments are implemented on the working situation where the speed reference is changed.Working situation 1 is implemented under attack in Case 4,and working situation 2 is implemented under attack in Case 7.
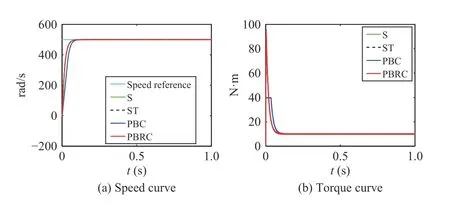
Fig. 13. Case 12 (a ui=2 , a yi=2, d =10 N·m, 0.4 s–0.6 s).

Fig. 14. Case 13 (a ui=5 , a yi=5, d =10 N·m, 0.4 s–0.6 s).
1) Working Situation 1 Under Case 4:In this case, the speed reference is set as –500 rad/s and the motor will start reversely. The simulation results are shown in Fig. 15.
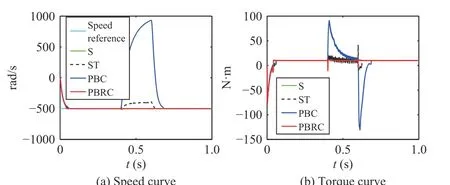
Fig. 15. Working situation 1 under Case 4 with attack ( ,, , 0.4 s–0.6 s).
aui=-0.9ayi=-0.9d=10 N·m
2) Working Situation 2 Under Case 7:In this case, the speed reference is set as 500 rad/s at the beginning, and then is changed to –1000 rad/s at 0.4 s, and is finally reverted to 500 rad/s at 1 s. The motor will start positively, then will decelerate in reverse at 0.4 s, and then start to accelerate positively at 1 s. The simulation results are shown in Fig. 16.
The above two cases study secure control under different working situations. As shown in Figs. 15 and 16, when attacks occur, the performance of controllers (23)–(25) will decline.In comparison, the performance of our controller (42) is resilient to attacks under different working situations.
J. Verification of Our Method Under Different Friction Coefficients
Consider some working situations in which the friction coefficient of the motor is increased (The initial friction coefficient of the motor is set as 0 N ·m·s). Working situation 1 is implemented under attack in Case 4, and working situation 2 is implemented under attack in Case 7.

Fig. 16. Working situation 2 under Case 4 with attack (a ui=-0.9,ayi=-0.9, d =10 N·m, 0.4 s–2.4 s).
1) Working Situation 1 Under Case 4:In this case, the friction coefficient of the motor is set to 1.8 N·m·s. The simulation results are shown in Fig. 17.

Fig. 17. Working situation 1 under Case 7 with attack ( ,, , 0.4 s–0.6 s).
aui=-0.9ayi=-0.9d=10 N·m

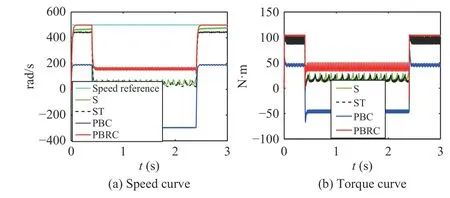
Fig. 18. Working situation 2 under Case 7 with attack ( aui=-0.9,ayi=-0.9, d =10 N·m, 0.4 s–2.4 s).
In the above two cases, we study secure control when the friction coefficient of the motor is increased. As shown in Figs. 17 and 18, when attacks occur and the friction coefficient of the motor is increased, the control performance of controllers (23)–(25) will fail, and the control performance of our controller (42) will decline during the attack.
V. CONCLUSIONS
In this paper, we have studied secure control for CPSs under quantified actuator and sensor attacks, which can maliciously increase or reduce control commands and sensor outputs. For attacked CPSs, we have proposed a defense scheme from the perspective of energy conversion. Then, a passivity-based robust controller has been designed to stabilize the attacked system. The effectiveness of our method has been verified through an industrial CPS. In the future, we will study two secure control problems: 1) when the direction of control commands and sensor outputs are reversed due to attacks; and 2) the saturation of actuator and sensor outputs caused by attacks.
APPENDIX A PROOF OF THEOREM 1


 IEEE/CAA Journal of Automatica Sinica2021年8期
IEEE/CAA Journal of Automatica Sinica2021年8期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Distributed Subgradient Algorithm for Multi-Agent Optimization With Dynamic Stepsize
- Kernel Generalization of Multi-Rate Probabilistic Principal Component Analysis for Fault Detection in Nonlinear Process
- Learning Convex Optimization Models
- An RGB-D Camera Based Visual Positioning System for Assistive Navigation by a Robotic Navigation Aid
- Robust Controller Synthesis and Analysis in Inverter-Dominant Droop-Controlled Islanded Microgrids
- Cooperative Multi-Agent Control for Autonomous Ship Towing Under Environmental Disturbances
