基于名单控制方法的探空测风数据质量分析*

杨国彬 郭启云 舒康宁 夏元彩

1 云南省气象信息中心，昆明 650034 2 中国气象局气象探测中心，北京 100081

提 要： 提出一种基于观测数据获取率、获取准时率、质量控制正确率和模式一致率的综合名单控制方法，使用2019年全国120个探空站测风数据对该方法进行验证，并对观测数据质量进行分析。结果显示：名单控制可以有效检查出观测数据存在问题的站点，名单站点观测数据相对于模式数据存在明显的系统性偏差，偏差和均方根误差相对于全国平均值都显著偏大。探空测风数据质量较好，四季风向、风速观测数据和模式数据较为一致，偏差分别在±1°和±1.5 m·s-1内；秋季风向一致性较好；夏季和冬季风速一致性低于春季和秋季；风向一致性春季和夏季随气压减小先减小后增大，秋季和冬季则相反；风速一致性随气压减小基本呈三峰型变化。

引 言

探空观测可以定点定时进行高空气象数据的观测，受地物、地形及人类活动的影响较小，其数据是我国主要的气象数据类型之一(高山，2014)；与各种遥测技术，如风廓线雷达相比(万蓉等，2011；吴志根等，2013；曲巧娜等，2016；王栋成等，2019)，它具有探测精度高，探测距离远的特点(郭启云等，2018b；曹晓钟等，2019；胡姮等，2019)。探空观测数据常被用于检验数值预报、再分析和遥感探测产品(赵天保和符淙斌，2009；王金成等，2017；程凯琪等，2020；郭启云等，2020b)，在科研、模式预报、天气分析、农业和各类气象服务之中发挥着重要的作用(吴泓锟等，2019；李芳芳等，2019；钱媛等，2019)。但由于电磁干扰、仪器变性、信号突失、下沉气流和仪器故障等情况会造成探空观测数据异常，而探空观测数据质量会直接影响到数据应用的效果，因此，在数据使用前需对其进行必要的质量控制(中国气象局，2010)。

大气风场资料是天气演变分析中最直观和最有价值的资料之一(周长艳等，2015)，根据大气风场的演变，尤其是高空风，可以了解中小尺度强对流天气发生发展的某些重要物理过程(张培昌等，2001；陈鹏等，2015;王丽吉和杨程，2018；李金辉等，2020)，比如高空槽脊的位置，高、低空急流的强度和深度，冷、暖平流的分布等；高时空分辨率和高精度的风场观测数据能够有效提高数值天气预报准确性，对提高强对流生成发展趋势预报能力有重要的意义(李娟等，2016)；此外，通过对高空风的研究，可以为风电开发企业和政府可持续开发利用风能资源提供很多参考(孟丹等，2019)。而探空测风是业务和科研主要高空风观测手段之一(董新宁等，2017)，因此，探空测风数据的质量一直是众多学者关注的重点，国内外已有很多机构和学者采用不同方法对探空测风数据进行质量控制(Durre et al，2006；Liao et al，2014；Houchi et al，2015；廖捷和周自江，2018；王丹等，2020)和质量评估(郭启云等，2018a)。

目前，我国针对探空测风数据的质量控制主要包括不同高度层的风速允许值范围检查和水平风场的垂直切变检查等(汪万林等，2011；Liao et al，2014)，或者通过模式预报场的评估结果进行质量控制(郭启云等，2020a)。黑名单检查可以剔除与背景场差异较大的观测站点(White，2003；St-James and Laroche，2005)，但是目前针对探空观测数据的黑名单通常来自和观测数据质量相关的一些先验信息，或者通过分析质量控制结果、比较观测和背景场的偏差等方式来确定(庄照荣等，2014)。现有对于探空观测数据的名单控制方法的研究存在定性化、判断依据单一等问题，本文旨在提出一种基于观测数据获取、常规质量控制和背景场检查的综合观测数据名单控制方法，据其将观测站点分别列入黑、黄、白名单，从而为数据用户提供参考；使用2019年全国探空测风数据对名单控制方法进行验证，并对2019年全国探空测风数据进行质量分析。

1 数据和方法

1.1 数 据

从全国综合气象信息共享平台(China Integrated Meteorological Information Service System，CIMISS)(熊安元等，2015)获取经过国、省、台站三级质量控制的带有质量控制码的2019年1月1日至12月31日119个(全国探空站共120个，沈阳站2019年4月1日起停止提供数据)探空站每天两个时次(00和12 UTC，下同)的探空测风数据。通过对质量控制结果的统计(表1)发现，2019年全国探空测风数据质量较好，各月正确数据占比均大于98%，数据缺测是探空测风数据存在的主要问题，可疑和错误均较少，部分月份会对数据进行修改。

模式背景场资料采用相同时段的中国气象局数值预报中心研发的全球与区域同化预报系统(Global-Regional Assimilation and Prediction System，GRAPES)的东北半球区域中尺度预报产品GRAPES_GFS v2.0(张萌等，2019)，空间分辨率为0.25°×0.25°，垂直方向从1 000～10 hPa，共26层；本文使用的是每个观测时次前一时次的12 h预报产品与观测数据进行对比分析。

在名单站点分析中引入欧洲中期数值预报中心(European Centre for Medium-Range Weather Forecasts，ECMWF，简称EC)东北亚地区高分辨率数值确定性预报产品进行对比分析，该数据空间分辨率为0.25°×0.25°，垂直方向从925～10 hPa，共19层，无30 hPa等压面。

参照日本气象厅(Japan Meteorological Agency，JMA)对探空测风数据的评估标准(http:∥qc.kishou.go.jp/)进行观测数据粗大误差的剔除，风速涉及的标准等压面包括1 000、925、850、700、500、400、300、250、200、150、100 hPa，风向涉及的标准等压面包括500、400、300、250、200、150 hPa，基于上述标准等压面数据展开研究。

1.2 方 法

基于CIMISS探空测风数据获取量、数据获取时间和数据质量控制码等有关信息计算观测数据获取率、获取准时率和质量控制正确率，并基于观测数据与GRAPES模式预报数据的偏差和均方根误差计算模式一致率。定义综合观测数据质量指数为R，则：

(1)

R=0.1R1+0.1R2+0.4R3+0.4R4

(2)

某站点某观测时次，R1为实际从CIMISS获取的数据总量与应该获取的数据总量的比率，只要任意从CIMISS获取到该站任意标准等压面的观测数据，则认为数据获取成功；R2为每个观测时次之后120 min内获取的数据总量与实际获取的数据总量的比率；R3为标准等压面上质量控制码为0(数据正确)、4(数据为修改值)的数据总量与实际获取的数据总量的比率。

1.2.1 模式一致率

以GRAPES模式预报产品作为背景场数据，通过计算观测数据与背景场数据的偏差(Bias)和均方根误差(RMSE)，根据偏差小于阈值的比例计算出对应的模式一致率R4。具体计算步骤如下：

若某时次某一标准等压面上，某探空站点观测数据为O，背景场数据为B，则观测偏差为：

Bias=O-H(B)

(3)

式中:H为观测算子，即通过水平和垂直的空间插值将格点上的背景场数据插值到站点。

某站点j观测数据与背景场数据的均方根误差为：

(4)

式中:M为计算时段内，第j个观测站点某一标准等压面的观测数据总量，则所有观测站点的平均均方根误差为：

(5)

式中:N为观测站点总量。

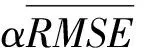
(6)

1.2.2 名单控制标准

通过上述方法计算各探空站在每个观测时次的数据质量因子，进行月平均，再根据式(2)计算得到各个站点的月平均综合观测数据质量指数R，根据表2中的名单控制标准(相关界限值通过一年的数据多次试验得出，能够较好地控制不同名单站点的比例)，将各观测站点列入不同的名单。站点若被列入黑名单，则认为其观测数据可能存在较为严重的错误；若被列入黄名单，则认为其观测数据可能存在错误；若被列入白名单，则认为其观测数据正确。

表2 各站点观测数据名单控制标准Table 2 List control standard for observation data of each station

1.2.3 质量分析指标

衡量任意两个气象要素之间关系密切程度的统计量是相关系数，对于观测数据(O)与背景场数据(B)的相关系数计算公式为：

(7)

式中：Cov(O,B)为观测数据与背景场数据的协方差;Var(O)、Var(B)分别为观测数据与背景场数据的方差。相关系数越大，说明该层等压面的观测数据和背景场数据相关程度越大，数据一致性越高，本文采用t检验法来对相关系数进行显著性水平检验。

2 结果和分析

2.1 名单控制结果

通过对2019年全国探空站点风向和风速分别进行名单控制，结果显示，2019年全国探空站点风向和风速观测数据质量均较好，所有站点风速逐月综合观测数据质量指数均大于85%，无任何站点被列入黑、黄名单；由图1可知，56146站风向1月被列入黄名单、2—3月被列入黑名单，其他月份所有站点风向综合观测数据质量指数均大于90%。

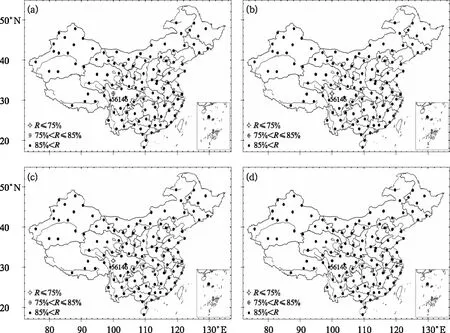
图1 2019年1月(a)，2月(b)，3月(c)，4月(d)风向名单控制结果Fig.1 The resultsa of wind direction list control for January (a), February (b), March (c) and April (d) 2019

2.2 名单站点分析

表3给出了56146站2019年逐月质量因子和综合观测数据质量指数。由表3可知，1—3月该站风向观测数据模式一致率R4<70%，这是由300 hPa 以上部分等压面偏差超过阈值造成的(图2a)，从而导致综合观测数据质量指数R<85%而被列入黄、黑名单。

从56146站1—4月风向观测数据与EC、GRA- PES模式数据平均偏差的垂直分布(图2b)可以看出，该站风向观测数据相对于两种模式数据均偏小，200 hPa及以上等压面观测数据相对于EC和GRAPES模式数据的偏差均超过阈值，因而可以确定为观测数据异常造成偏差较大，导致模式一致率较低。因为该站2月和3月连续出现在黑名单中，对其进行了跟踪反馈，经与台站核实，判定为L波段测风雷达标定存在问题造成数据异常，4月重新对雷达进行找北标定后，观测数据不再有问题，5月以后风向观测数据模式一致率R4均为100%(表3)。这表明，本文提出的名单控制方法可以有效检查出观测数据存在问题的站点，对名单站点进行跟踪解决后可以有效提高观测数据质量。

表3 56146站2019年逐月质量因子和综合观测数据质量指数(单位：%)Table 3 Monthly quality factor and comprehensive observation data quality index at Station 56146 in 2019 (unit: %)

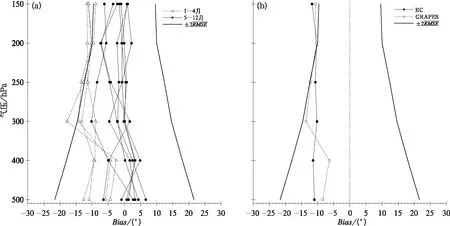
图2 56146站观测数据与GRAPES模式数据逐月偏差(a)和 1—4月观测数据与EC、GRAPES模式数据平均偏差(b)Fig.2 The monthly Bias between observation data and GRAPES mode data (a) and average Bias between observation data and EC and GRAPES model data from January to April (b) at Station 56146

为进一步分析名单站点与全国所有站点平均结果的差异，图3分别给出了不同等压面56146站和全国平均偏差和均方根误差，由图可知，所有等压面56146站偏差相对于全国平均值偏差大于10°，均方根误差较全国平均值偏大5°～7°；56146站偏差和均方根误差相对于全国平均值的偏差极大值均出现在150 hPa，分别为11.6°和7.4°。

图3 不同等压面56146站和全国平均偏差(a)和均方根误差(b)Fig.3 The Bias (a) and RMSE (b) of Station 56146 and national average with different mandatory levels

由上述分析可知150 hPa相对偏差是所有等压面里面最大的，因此图4给出了2019年1—4月56146站150 hPa的风向观测数据、EC和GRAPES模式数据逐时次变化序列。由图可知，三种数据随时间变化的趋势一致；两种模式数据差异不大，而观测数据相对于模式数据存在明显的系统性偏小，1月15日12 UTC开始系统性偏差显著增大，2、3月偏差较大，对雷达重新进行找北标定后4月7日00 UTC开始偏差显著减小。1—4月观测数据与EC、GRAPES模式数据平均偏差分别为-13.2°、-10.4°，-13.4°、-12.5°，-12.3°、-12°，-9.5°、-8.8°。

图4 2019年1月(a)，2月(b)，3月(c)和4月(d)56146站150 hPa的 风向观测数据、EC和GRAPES模式数据逐时次变化序列Fig.4 Hourly distribution of wind direction observation data, EC and GRAPES model data at Station 56146 at 150 hPa in January (a), February (b), March (c) and April (d) 2019

2.3 观测数据质量分析

为了进一步分析2019年全国探空测风的风向和风速数据质量，分别从不同标准等压面不同季节的风向和风速观测数据与GRAPES模式数据的偏差、均方根误差、相关系数三个方面对2019年探空测风数据进行质量分析，相关指标的计算和统计都是基于标量法进行的。

2.3.1 偏差

由表4可知，四季各等压面风向偏差均在±1°内。春季500～250 hPa为负偏差，其他等压面为正偏差，负偏差随气压减小而减小，正偏差则反之；夏季除250和200 hPa外均为正偏差，总体来说偏差绝对值随气压减小先减小后增大；秋季各等压面正负偏差交替出现，偏差绝对值随气压减小先增大后减小；冬季各等压面均为负偏差，偏差绝对值随气压减小基本呈“W”型变化。所有等压面绝对偏差平均值秋季远小于其他季节；不同等压面各季节绝对偏差在500 hPa：冬季>春季>夏季>秋季，400 hPa：夏季>秋季>冬季>春季，300 hPa：冬季>秋季>春季>夏季，250 hPa：冬季较大，200和150 hPa：春季>夏季>冬季>秋季。

表4 各季节各等压面风向偏差(单位：°)Table 4 Bias of wind direction at different mandatory levels in each season (unit: °)

由表5可知，四季各等压面风速偏差均在±1.5 m·s-1内，1 000 hPa均为负偏差，其他等压面以正偏差为主，偏差随气压减小基本呈三峰型变化，峰值分别出现在1 000、700和200 hPa。春季和冬季250和200 hPa偏差较大，夏季和秋季1 000 hPa偏差较大。所有等压面绝对偏差平均值冬季>夏季>秋季>春季；不同等压面各季节绝对偏差在1 000 hPa：秋季>夏季>冬季>春季，925 hPa:春季>秋季>夏季>冬季，850和500 hPa夏季偏差较大，其他等压面冬季较大。

表5 同表4，但为风速(单位：m·s-1)Table 5 Same as Table 4, but for wind speed (unit: m·s-1)

2.3.2 均方根误差

由表6和表7可知，四季各等压面风向均方根误差在4.58°～15.65°，随气压减小而减小，不同等压面均方根误差大小均是夏季>秋季>春季>冬季。四季各等压面风速均方根误差在2.07～4.54 m·s-1，随气压减小先增大后减小，700 hPa及以下等压面均方根误差均小于3 m·s-1，300和250 hPa等压面均方根误差较其他等压面大；不同等压面各季节均方根误差在1 000 hPa秋季>冬季>夏季>春季，其他等压面春季最大、秋季最小。

表6 各季节各等压面风向均方根误差(单位：°)Table 6 RMSE of wind direction in different mandatory levels in each season (unit: °)

表7 同表6，但为风速(单位：m·s-1)Table 7 Same as Table 6, but for the wind speed (unit: m·s-1)

2.3.3 相关系数

由表8可知，四季各等压面风向相关系数均大于0.80，并且通过了0.01的显著性水平检验，均随气压减小而增大；不同等压面各季节相关系数在500 hPa夏季、秋季较冬季、春季大，400 hPa及以上等压面秋季、冬季较春季、夏季大。

表8 各季节各等压面风向相关系数Table 8 Correlation coefficient of wind direction at different mandatory levels in each season

由表9可知，四季各等压面风速相关系数在0.57～0.95，都通过了0.01的显著性水平检验，春季、夏季随气压减小先增大后减小，秋季、冬季925 hPa 较上下等压面略大，850～100 hPa随气压减小先增大后减小；700 hPa以下等压面各季节相关系数差异不大，其他等压面冬季最大夏季最小。

表9 同表8，但为风速Table 9 Same as Table 8, but for wind speed

3 结 论

本文提出一种基于观测数据获取、常规质量控制和背景场检查的综合观测数据名单控制方法，使用2019年全国探空测风数据对该方法进行了验证，对名单控制结果进行了分析，并对探空测风的风向和风速数据进行质量分析，得到以下主要结论：

(1)2019年全国探空测风数据质量较好，数据缺测是探空测风数据存在的主要问题，可疑和错误数据均较少。名单控制可以有效检查出观测数据存在问题的站点，名单站点观测数据随时间变化的趋势与不同模式数据一致，但相对于模式数据存在明显的系统性偏差，偏差和均方根误差相对于全国平均值都显著偏大。

(2)相对于模式数据，四季各等压面风向偏差在±1°内，春季、夏季偏差绝对值随气压减小先减小后增大，秋季、冬季则随气压减小先增大后减小；春季250 hPa以下等压面观测数据小于模式数据，250 hPa以上则相反，夏季除250和200 hPa外观测数据均大于模式数据，秋季观测数据与模式数据较为一致，正负偏差交替出现，冬季所有等压面观测数据小于模式数据。四季各等压面风速偏差在±1.5 m·s-1内，偏差随气压减小基本呈分别在1 000、700和200 hPa出现峰值的三峰型变化；除1 000 hPa外，观测数据基本都大于模式数据，总体来说，春季、秋季较夏季、冬季观测数据与模式数据更为一致。

(3)相对于模式数据，四季各等压面风向均方根误差在4.58°～15.65°，随气压减小而减小；不同等压面均方根误差大小均是夏季>秋季>春季>冬季。四季各等压面风速均方根误差在2.07～4.54 m·s-1，随气压减小先增大后减小；除1 000 hPa外，各等压面均方根误差春季最大、秋季最小。

(4)四季风向、风速观测数据和模式数据显著相关，风向平均相关系数均大于0.8，风速相关系数在0.57～0.95，各季节风向、风速相关系数基本随气压减小而增大。所有等压面风向相关系数平均值为秋季>冬季>夏季>春季；风速夏季略小，其他季节相当。