The Significant Role of Radiosonde-measured Cloud-base Height in the Estimation of Cloud Radiative Forcing
Hui XU ,Jianping GUO* ,Jian LI ,Lin LIU ,Tianmeng CHEN ,Xiaoran GUO,2 ,Yanmin LYU,Ding WANG,Yi HAN,2,Qi CHEN,and Yong ZHANG
1State Key Laboratory of Severe Weather,Chinese Academy of Meteorological Sciences,Beijing 100081,China
2College of Earth Sciences,University of Chinese Academy of Sciences,Beijing 100049,China
3Meteorological Observation Center,China Meteorological Administration,Beijing 100081,China
ABSTRACT The satellite-based quantification of cloud radiative forcing remains poorly understood,due largely to the limitation or uncertainties in characterizing cloud-base height (CBH).Here,we use the CBH data from radiosonde measurements over China in combination with the collocated cloud-top height (CTH) and cloud properties from MODIS/Aqua to quantify the impact of CBH on shortwave cloud radiative forcing (SWCRF).The climatological mean SWCRF at the surface(SWCRFSUR),at the top of the atmosphere (SWCRFTOA),and in the atmosphere (SWCRFATM) are estimated to be −97.14,−84.35,and 12.79 W m−2,respectively for the summers spanning 2010 to 2018 over China.To illustrate the role of the cloud base,we assume four scenarios according to vertical profile patterns of cloud optical depth (COD).Using the CTH and cloud properties from MODIS alone results in large uncertainties for the estimation of SWCRFATM,compared with those under scenarios that consider the CBH.Furthermore,the biases of the CERES estimation of SWCRFATM tend to increase in the presence of thick clouds with low CBH.Additionally,the discrepancy of SWCRFATM relative to that calculated without consideration of CBH varies according to the vertical profile of COD.When a uniform COD vertical profile is assumed,the largest SWCRF discrepancies occur during the early morning or late afternoon.By comparison,the two-point COD vertical distribution assumption has the largest uncertainties occurring at noon when the solar irradiation peaks.These findings justify the urgent need to consider the cloud vertical structures when calculating the SWCRF which is otherwise neglected.
Key words:cloud base height,radiosonde,radiative forcing,China,climatology
1.Introduction
Clouds cover approximately two-thirds of Earth's surface area and play a significant role in both the Earth’s radiative balance and hydrological cycle (e.g.,Ramanathan et al.,1989
;Stephens et al.,2012
;Chen et al.,2016
;Zhou et al.,2016
;Min et al.,2020
).It is well established that clouds exert a cooling effect by reflecting incoming shortwave radiation back to space,and also a warming effect by trapping outgoing long-wave radiation (Slingo and Slingo,1988
;Wang and Key,2003
;Min and Zhang,2014
).The net magnitude of this cloud-induced perturbation in the radiative balance at the surface (SUR),at the top of the atmosphere (TOA),and in the atmosphere (ATM) is typically measured in terms of cloud radiative forcing (CRF,Shupe and Intrieri,2004
).The CRF in the ATM,which represents the energy absorbed in the cloud layer,is shown to significantly affect the atmospheric circulation and the water cycle,thereby altering global weather and climate (Wang et al.,2007
;Henderson et al.,2013
;Lü et al.,2015
).However,large uncertainties exist regarding the estimation of the CRF (especially the CRF in ATM) in current climate and weather models.The magnitudes of the CRF are highly dependent on the cloud vertical structures,including cloud-top height(CTH),cloud-base height (CBH),cloud thickness (CT),and the vertical overlapping pattern of cloud layers(Ramanathan et al.,1989
;Mitchell and Finnegan,2009
;Li et al.,2019
).The impact of cloud vertical structures on the CRF is often investigated through the role of the CTH in the estimation of the CRF at the TOA (Loeb et al.,2012
;Chen and Fu,2018
).However,recent studies suggest a strong dependence of the CRF on the CBH,which considerably affects the land-atmosphere energy exchanges.For example,Kato et al.(2011)
indicated that the underestimation of the CBH results in an increase of the global annual mean of instantaneous surface downward long-wave irradiance.Viúdez-Mora et al.(2015)
quantified the average CRF at the surface using the CBH determined from ceilometer measurements and demonstrated that the CRF decreased with CBH at a rate of 4−5 W mkmwith the average CRF observed to be in the range of 50−80 W m.George et al.(2018)
investigated the relationships of the CBH with the CRF at the surface and TOA using soundings and found that the shortwave CRF depended on the total depth of cloud layers,whereas the longwave CRF depended on the height of cloud layers.However,there are few previous studies on the CBH impact on the estimates of the CRF in the atmosphere,and thus the role of the CBH upon the CRF estimates remains largely unknown,particularly in China.One of the major obstacles in quantifying the impact of the CBH on the CRF lies in the difficulties in determining the CBH on a large scale.On the one hand,ground-based instruments such as lidars,ceilometers,and millimeter wavelength cloud radars (e.g.,Martucci et al.,2010
;Costa-Surós et al.,2013
),gain competitive edges in determining CBHs for their relatively higher accuracy and stronger temporally continuous sampling capabilities (e.g.,Sharma et al.,2016
;Zhou et al.,2019
).However,these instruments are generally deployed at very few locations (Dai et al.,2006
;Zhang et al.,2019
),thereby having poor spatial representation.On the other hand,the CBH cannot be directly retrieved from passive satellite observations such as the moderate resolution imaging spectroradiometer (MODIS)onboard both Terra and Aqua.Active sensors such as the Cloud-Aerosol Lidar with Orthogonal Polarization(CALIOP) onboard the CALIPSO and the millimeterwavelength cloud profiling radar (CPR) onboard the Cloud-Sat can resolve the vertical distribution of cloud layers,including the CBH and CTH (Winker et al.,2009
;Wang et al.,2015
).However,in terms of the accuracy of the CBH detected from the aforementioned active sensors,large uncertainties exist due to the strong attenuation of radar or laser beams,especially in the presence of deep convective clouds(e.g.,Zhang et al.,2017
;Zhou et al.,2019
).The operational radiosonde networks have higher detection accuracy of cloud layers,making it possible to determine CBH over a large spatial domain,albeit with poor temporal coverage (Poore et al.,1995
;Zhang et al.,2010
).Therefore,the present study aims to investigate the impact of the CBH on the estimated shortwave CRF (SWCRF) by using a high-resolution dataset from a radiosonde network in China that spanned nine years (2010−2018).As a first step,the climatology of SWCRF at the surface (SWCRF),at the top of the atmosphere (SWCRF),and in the atmosphere(SWCRF) is compiled,by combining the CBH from the radiosonde measurements and the CTH and cloud properties from MODIS for the summers spanning 2010 to 2018.The accuracy of the SWCRF climatology is established through comparisons with the Clouds and the Earth's Radiant Energy System (CERES) product.Then,the SWCRFs calculated under four scenarios which vary the vertical profile of cloud optical depth (COD) are compared to deduce the role of the CBH on the estimation of the SWCRF.In addition,we will test the sensitivity of both the CBH and solar zenith angle on the SWCRF.2.Data and Methods
2.1.Data
2.1.1.Radiosonde derived CBH
Radiosonde data provide in situ measurements of atmospheric environmental variables,including temperature,pressure,RH,wind speed,and wind direction,which is recognized to be able to derive the overlapping pattern of cloud in the vertical direction.The China radiosonde network (CRN)consists of 120 radiosonde sites across China,in which the high-resolution (5−8 m) sounding balloon is launched twice per day at 0800 LST (LST=UTC+8) and 2000 LST (Guo et al.,2016
,2019
).Based on these fine-resolution radiosonde measurements,the CBHs are calculated for the summer (June−August) during the period from 2010 to 2018 using the improved relative humidity (RH) threshold method (Zhang et al.,2018
).Coincidently,up to two additional soundings are launched occasionally at 1400 LST and 0200 LST in summer during certain intensive observing periods at selected stations (Guo et al.,2016
;Lou et al.,2019
).Given the spatial inhomogeneity,the CBHs from all sites are interpolated onto a regular 5° × 5° grid,following the method byZhang et al.(2018)
.The significant diurnal variation of summertime clouds in China (Chen et al.,2018
) justifies the use of the 1400 LST soundings to derive CBHs unless otherwise noted.This is expected to better match with the CTH products from MODIS onboard Aqua,one of the polar-orbiting satellites.2.1.2.MODIS level-3 daily cloud products
The MODIS instrument,an important payload of both Terra and Aqua satellites,can observe the Earth with a total swath width of 2300 km,with a revisit cycle of one to two days,depending on the location (Remer et al.,2005
).The MODIS has 36 spectral bands ranging from 0.4 to 14.2 μm(Salomonson et al.,1989
),providing global coverage of cloud optical and physical parameters at both granule and grid levels (Platnick et al.,2003
).As one of important cloud optical properties,cloud optical depth (τ
) can affects the shortwave CRF by reflecting the attenuation of radiation intensity by cloud in the transmission path (Chen et al.,2019b
).As the global gridded product,the level-3 cloud products of MODIS are made publicly available on a grid size of 1° ×1° at daily,8-day,and monthly timescales (Menzel et al.,2008
).Therefore,the MODIS level-3 daily cloud products onboard Aqua (MYD08_D3) are used in this study to characterize the optical and physical properties of cloud tops.In order to be collocated with the CBHs derived from the 1400 LST radiosonde data,the MODIS cloud products,including the CTH (h),the daily averaged liquid and ice COD(τ
),liquid and ice cloud effective radius (r),as well as cloud fraction (ƒ),are resampled to 5° latitude× 5°longitude grid by simply averaging out the original MODIS products.2.1.3.Land surface albedo
The MODIS albedo product (MCD43) could provide both white-sky albedos and black-sky albedos for spectral and broad bands.The MCD43 is a daily product,obtained by the surface reflectance observations built up over a 16-day period (Schaaf et al.,2002
).As a climate modeling grid product,MCD43C3 provides albedo d ata at a spatial resolution of 0.05° latitude× 0.05° longitude grid.In the present study,a climatology of daily-averaged surface albedo (α)data was built using nine years (2010−18) of MCD43C3 black-sky visible albedo,in which only thoseα
values with a quality flag less than or equal to two were used.2.1.4.CERES radiative flux data
The Clouds and the Earth's Radiant Energy System(CERES) instrument directly measures global radiance at the TOA.By combining the MODIS and GEOS-derived cloud properties,CERES could also provide the radiance at the surface (Wielicki et al.,1996
).The high accuracy and robustness of the CERES radiance products in revealing Earth’s energy imbalance have been adequately verified(Loeb et al.,2012
;Allan et al.,2014
;Trenberth et al.,2014
).As such,the CERES Synoptic TOA and surface fluxes and clouds (SYN) products under the clear-sky and all-sky conditions with a spatial resolution of 1° × 1° are used here as “ground-truth” to validate the SWCRF estimated by the radiative transfer model.Prior to its application in the following analysis,we first calculate the CERES SWCRFand SWCRFusing the clear-sky and all-sky incoming and outgoing SW flux at the TOA and surface,respectively.Then,the CERES-derived SWCRF are resampled from a 1° × 1° to 5° × 5° latitude/longitude grid.2.1.5.Radiative transfer model RRTM_SW
The shortwave rapid radiative transfer model(RRTM_SW) has been used to calculate both atmospheric radiative fluxes and heating rates for the spectral wavenumber of 820−50 000 cm(Clough et al.,2005
).By utilizing the correlated-k approach,the fluxes provided by RRTM SW are accurate,computationally efficient,and fast.Due to its high accuracy and efficiency,the RRTM_SW has been widely applied to those studies associated with atmospheric radiative transfer and general circulation models (GCMs)(e.g.,Thampi and Roca,2014
;Verlinden and de Szoek,2018
).2.2.Methods
2.2.1.Calculation of SWCRF
Here,the SWCRF (ΔF;W m) is defined as the difference of net solar flux between an environment with clouds and one without clouds present at the surface,at the TOA,or in the atmosphere,which can be expressed as:
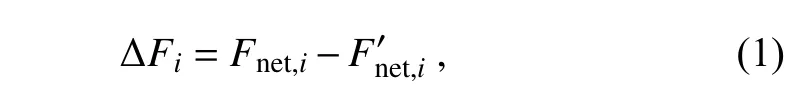
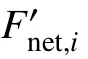
F
can be calculated as the difference between the downwelling flux with cloud (F
) and upwelling flux with cloud (F
),which is formulated as:
Combining Eqs.(1)−(3),we obtain the following expression:
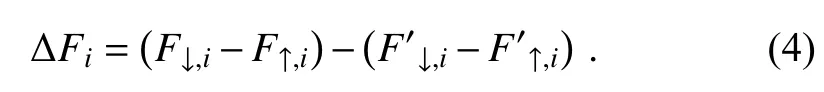
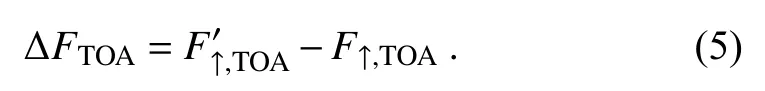
Meanwhile,the SWCRF in the atmosphere (ΔF) is defined as:
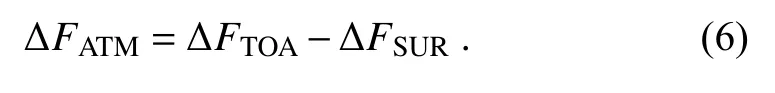
2.2.2.Assumption concerning the vertical profile of COD
Normally,the vertical distribution of COD is assumed to be uniform in the current climate model.Here,we define four scenarios regarding the vertical distribution of COD,including a two-point distribution (Scenario 1),a uniform distribution (Scenario 0 &Scenario 2),and a normal distribution (Scenario 3),which are described as follows:
(1)Two-point distribution
The two-point distribution assumes the total COD is concentrated in only two cloud layers.Thus,the COD for each cloud layer is 1/2 of the total COD.In addition,we define the two heights of the cloud layer to be 1/4 and 3/4 of the total cloud height.The distribution can be formulated as follows:
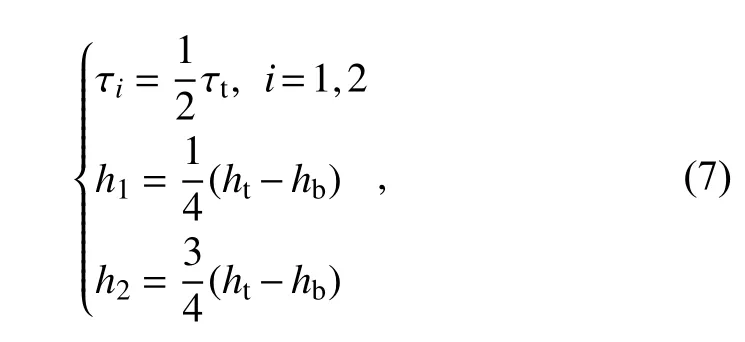
(2)Uniform distribution
The uniform distribution assumes that the total COD is uniformly distributed across the cloud layers in the vertical,and the COD of the ith cloud layer is expressed as follows:
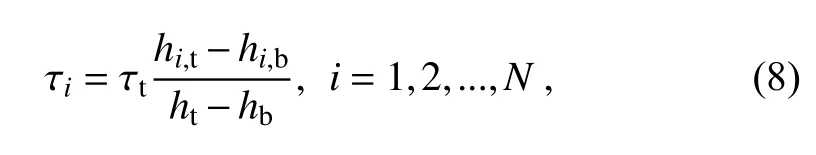
where the h,and hstand for the top and base height for the ith cloud layer,respectively,and N represents the number of the cloud layer.
(3)Normal distribution
The symmetrical distribution of many natural processes and phenomena is the normal distribution.In this study,we assume the vertical distribution of COD is a normal distribution.For the given interval [μ
±3σ
],the probability of the actual COD falling within that interval is nearly 1.0 (Mishra and Datta-Gupta,2018
).Thus,the COD of the ith cloud layer can be described as follows: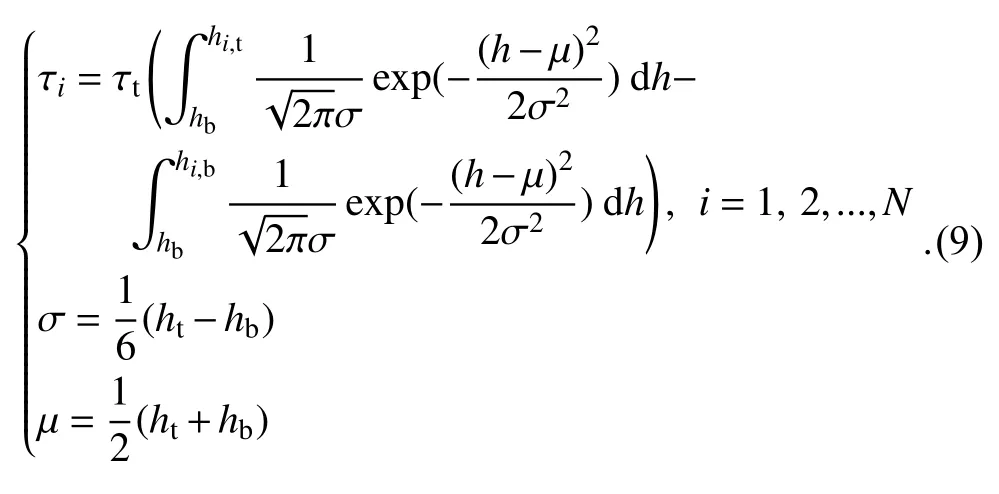
2.2.3.Radiative transfer calculations
Table 1
.Schematically shown inFig.1
is an example of the vertical profile of the COD as a function of the normalized total COD.
Table 1.Summary for the vertical profile scenarios of cloud optical depth (COD) assumed in the calculation of cloud optical depth,which is an important input for the calculation of cloud radiative forcing.
2.2.4.Sensitivity analysis
We perform a sensitivity analysis to better understand the impact of CBH on the SWCRF.This consisted of a series of experiments on the CRF estimation,that have been conducted by running the RRTM_SW with varying CBH values,under different cloud vertical profile patterns of COD.In an ideal experiment,the liquid effective particle radius is set to be uniform at 15 μm,whereas the solar zenith angles(SZA) are set to 0°,30°,and 60°,respectively.The CBH values are set to increase from 0.5 km upwards until 5.0 km at 0.5 km intervals,and the increase in CBH each time is defined as Δh.The total COD is constant,and the vertical profile of COD is calculated using the cloud-top height (h)and the changed cloud-base height (h+Δh).
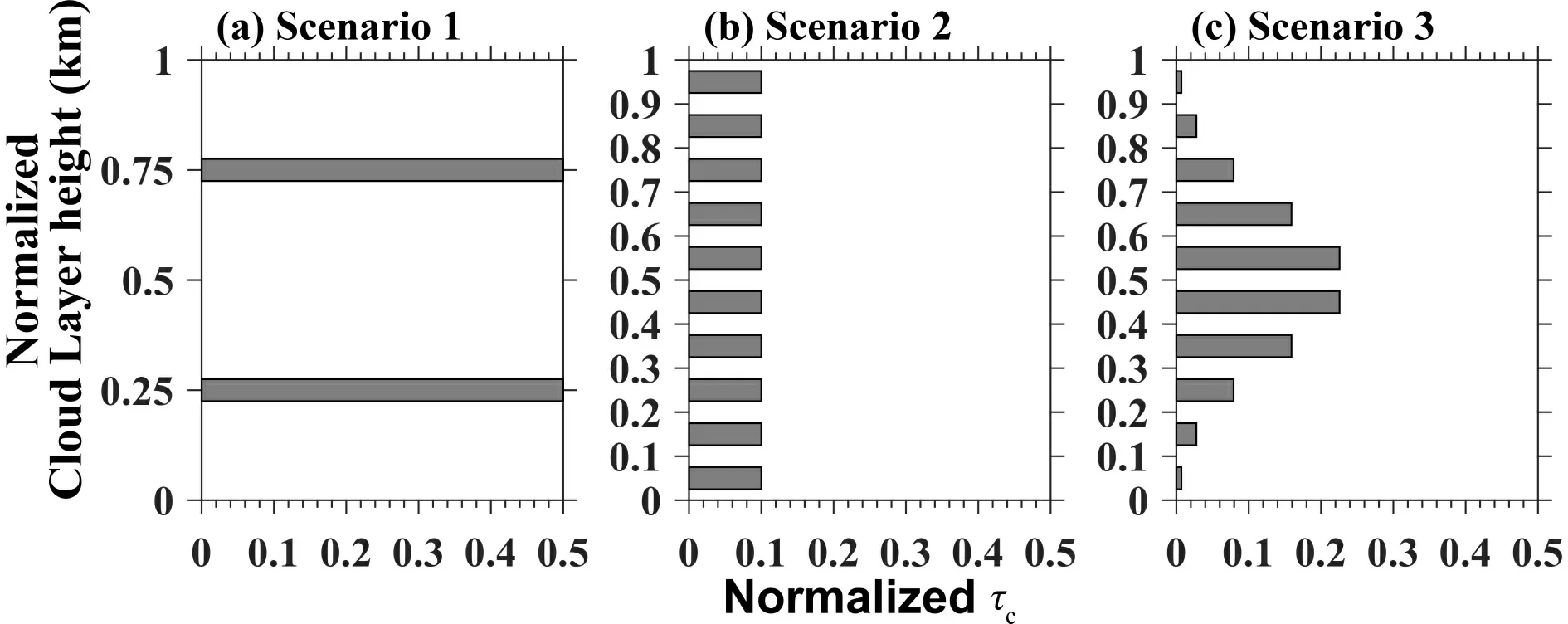
Fig.1.The normalized cloud optical depth (COD;τc) shown as a function of normalized cloud height (km) for three different vertical profile Scenarios of COD:(a) Scenario 1,(b) Scenario 2,and (c) Scenario 3,based on the assumption of the true number of the cloud layer is equal to 10 and the height of cloud is uniform.
3.Results and discussion
3.1.Distribution of CTH,CBH and cloud thickness in China
Figure 2
presents the geographic distributions of summertime cloud properties in China within 5° latitude × 5° longitude grid boxes during the period from 2010 to 2018,including the CTH derived from the MODIS/Aqua,the CBH derived from the radiosonde measurements,and the cloud thickness (CT).The mean CTH,CBH,and CT correspond to 7.23 km,3.56 km,and 4.71 km above ground level(AGL),respectively.Overall,the CTH exhibits a noticeable geographical variability in summer across China.For instance,the cloud top tends to develop much higher over the Tibetan Plateau (TP) and South China Sea (SCS),where the South Asian Monsoon and mesoscale convective systems most frequently occur (Wang and Ho,2002
;Chen et al.,2019a
).In the latitude zone between 30°N and 45°N,western China has higher CTHs than eastern China,which is likely due to the terrain difference between eastern and western China.By comparison,the summertime CBHs exhibit a“northwest-high-southeast-low” pattern:CBHs as high as 4.0 km AGL or higher are found in Northwest China versus much smaller CBHs (less than 3.0 km AGL) in Southeast China.The lowest CBH tends to occur in the coastal region of East China,and the northern part of the South China Sea,which is lower than 2.0 km AGL.This could be attributed to a lower lifting condensation level due to higher dew points near the coast.Another pronounced signal is evidenced by the decreasing trend of CT with increasing latitude,indicating that the CT spatial pattern exhibits a strong south-to-north gradient,with greater CT in southern China.Figure 3
shows the spatial distributions of heightresolved occurrence frequency for the CTH,CBH,and CT,respectively.The probability density function (PDF) of CTH peaks at around 6−8 km AGL and features a heavy tail.Specifically,most of the CTHs (~80%) are mainly located above 5 km,indicating the dominance of middle-and high-level clouds in China.By comparison,the tail shifts towards low CBHs,and the CBHs falling within 0−3 km are responsible for approximately 65% of all cases.Interestingly,the PDF of cloud thickness exhibits a roughly normal distribution,with more than half of the CTs falling within 2−5 km.Overall,the frequency distributions of CTH and CBH revealed here are broadly consistent with the previous remote sensing studies (e.g.,Yin et al.,2015
;Chen et al.,2018
).Note that the PDFs of CTH,CBH,and CT given in 0.1 km vertical range bins are also shown inFig.3
.The peak in the PDF of CBH is generally located at 1−2 km,and then gradually decreases with height above 2 km,indicating that the bases of cloud layers are lower than 2 km AGL under most circumstances.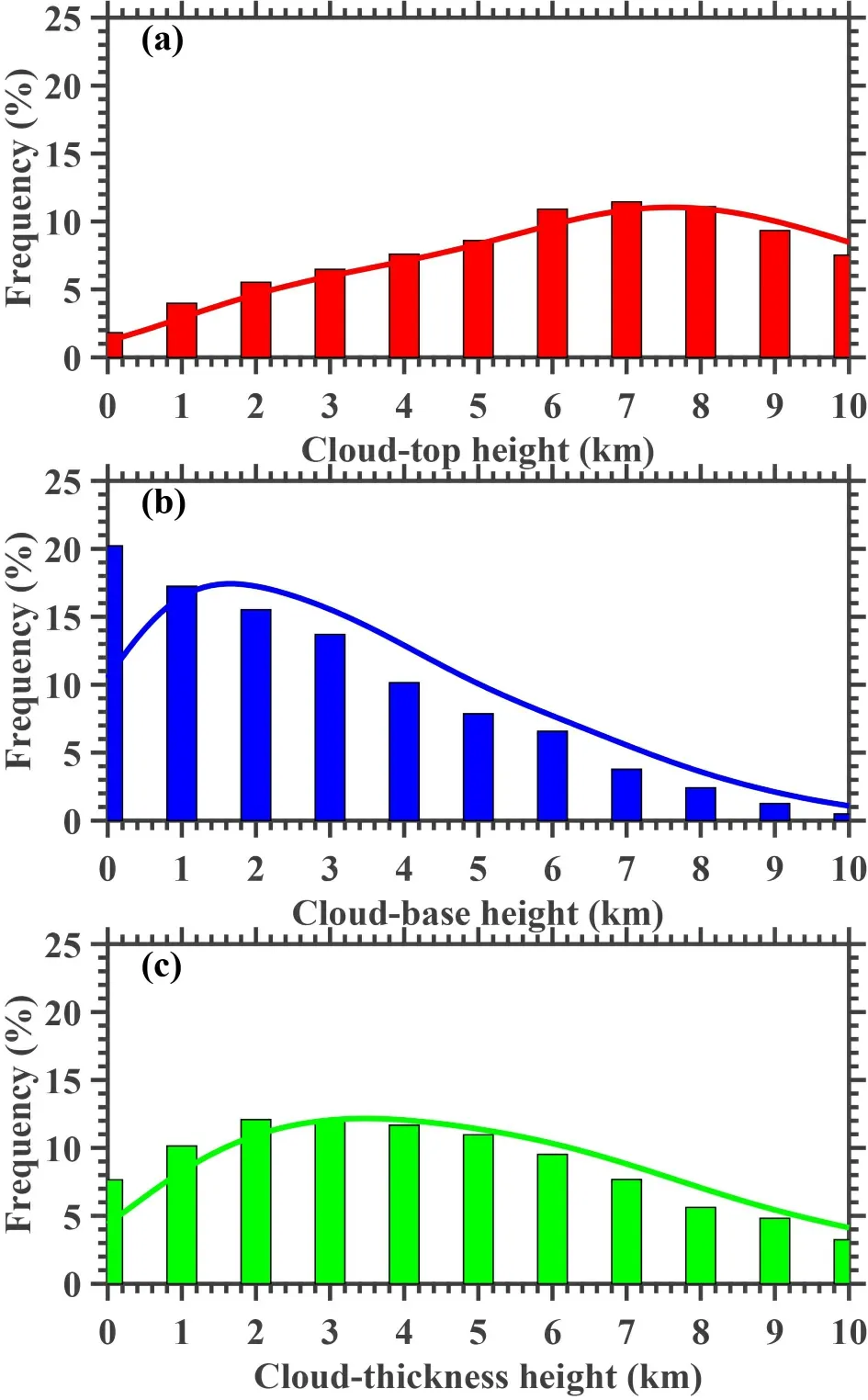
Fig.3.The frequency distribution of (a) CTH (red bars),(b)CBH (blue bars),and (c) cloud thickness (green bars) over China in summer for the period from 2010 to 2018.The data in the histogram are pooled into 1.0 km bins.The red,blue,and green curves depict the kernel density estimate (KDE) of the probability distribution function (PDF) for CTH,CBH,and cloud thickness,respectively.
Figure 4
illustrates the percentile analysis for CBH,CTH,and CT as a function of latitude.It is clear that CBHs tend to increase with latitude,reaching the peaks in the latitude range between 37.5°N and 42.5°N.Coincidently,the planetary boundary layer height (PBLH) exhibits an interesting spatial pattern of “northwest high southeast low” in China(i.e.,Zhang et al.,2018
;Guo et al.,2019
;Xu et al.,2021
).Therefore,the dependence of CBH on latitude resembles the spatial pattern of PBLH in China,to some extent.This could be attributed to the spatial discrepancy of soil moisture (Xu et al.,2021
) since the dominant factor driving the development of the boundary layer comes from sensible heat flux that is closely associated with soil moisture.In particular,as the latitude increases,the gap of CBH shifts towards larger values particularly when the CBH is below the 50th percentile,suggesting a patchier CBH distribution at high altitude regions in China (under lower cloud base circumstances).As for the linear meridional trends in CBH percentiles,the lower percentiles of CBH increase slowly,in contrast to the higher percentiles of CBH.The trends of high CBHs (e.g.,80th and 90th percentile),on average,are much larger than those of low CBHs (e.g.,50th percentile and below).Regarding the CTHs,low percentiles of CTHs do not show any pronounced latitudinal dependence,while high percentiles of CTHs tend to decrease with increasing latitudes.The average trend of high CTHs (90th percentile) is far less than twice as large as the median CTHs (50th percentile).This is also the case for CT,since the high percentiles of CTs decrease much more rapidly with the increasing latitude compared to the median percentile of CT.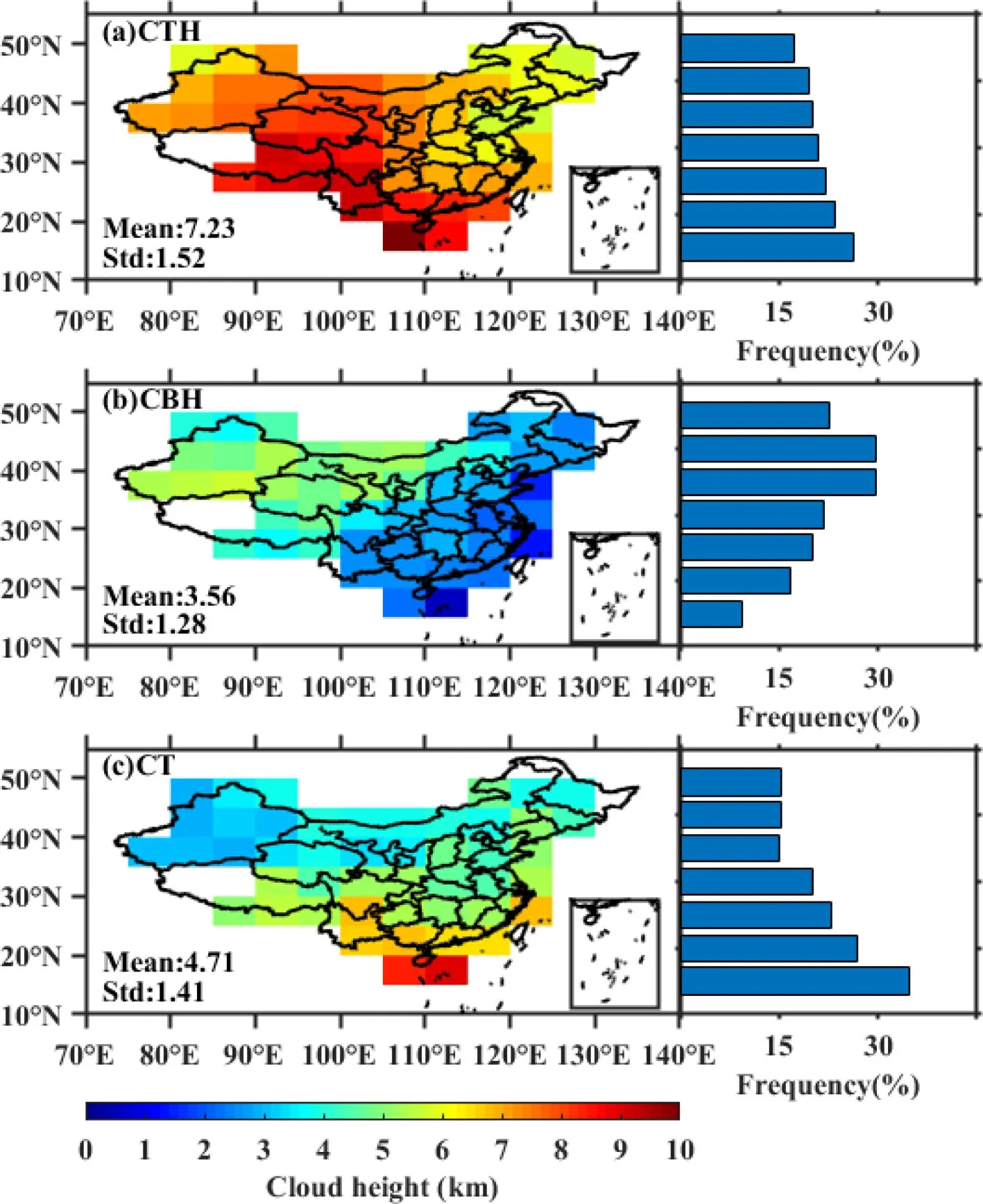
Fig.2.Spatial distributions of (a) cloud-top height (CTH) from MODIS/Aqua,(b) cloud-base height (CBH) from radiosonde measurements,and (c) cloud thickness (CT) from MODIS/Aqua over China in summer (June−August) for the period from 2010 to 2018.The blue bars on the right-hand side represent the frequency of cloud height in different latitudes.
3.2.Evaluation of the simulated SWCRF climatology
Using the radiosonde-derived CBH and the MODISderived CTH as the two main input parameters,the SWCRF climatology is simulated in summer over China.In order to confirm the reliability of this climatology,the simulated SWCRF is compared with its counterpart from CERES inFig.5
.In general,the SWCRFand SWCRFare negative,whereas the SWCRFis positive.This means that clouds tend to exhibit a cooling effect at the SUR and TOA,but exhibit a warming effect in the ATM during summer over China.A high correlation (R=0.8) is found between the simulated SWCRFand CERES observation.Similarly,the SWCRFagrees well with CERES (R=0.79).These robust relationships indicate that the simulated SWCRF climatology is consistent with the CERES measurements at the TOA and the surface.However,there are large differences between the simulated and the CERES-derived SWCRF.We hypothesize that the probable reason for this could be the inability of the satellite observation of CERES to capture the cloud bottom.To confirm our hypothesis,we conducted a correlation analysis concerning the absolute difference between the CERES-derived and the simulated SWCRF(ΔSWCRF) versus cloud height.Figure 6 a
shows that the biases which exist in the CERES-derived SWCRFpositively correlate with cloud thickness,while it negatively correlates with cloud bottom (Fig.6b
).This indicates that the biases of CERES SWCRFtend to increase when thick clouds with low base height are present.Also,the negative SWCRFfrom the CERES product (red points inFig.6
)further demonstrates that large biases from satellites often occur for low and thick clouds.The reason for this could be that the satellite observation could not provide an accurate estimation of cloud bottom,especially in the presence of thick clouds with low bottoms.3.3.Spatial pattern of SWCRF
Figure 7
presents the spatial distribution of summertime SWCRF,SWCRF,and SWCRFin China during the period from 2010 to 2018.The mean values of SWCRF,SWCRFand SWCRFare −97.14 W m,−84.35 W m,and 12.79 W m,respectively.This result is consistent with previous studies.For example,Yu et al.(2001)
estimated SWCRFvalues as large as −85.0 W musing the observations from the Earth Radiation Budget Experiment (ERBE) experiment during summertime in eastern China.Similarly,Wang et al.(2004)
obtained the mean SWCRFover the Yangtze River−Huaihe River valley at about −110.0,−100.0,and −70.0 W min June,July,and August,respectively.In particular,relatively small SWCRFis observed in Northwest China (Fig.7a
),which may be explained by the thin cloud layer caused by the high CBH and low CTH common to this region (Fig.2
).By comparison,the SWCRFin central and eastern China is high,which is attributed to the large cloud thickness in this region.This result demonstrates that the SWCRFlargely depends on the cloud thickness but has no relation with the cloud base.Our results are consistent with previous findings (e.g.,Zhang et al.,2017
;George et al.,2018
),which suggests that cloud depth contributes significantly to the estimate of SWCRF.The spatial distribution of SWCRF(Fig.7b
),to some extent,is roughly similar to that of the SWCRF.This indicates that SWCRFis also influenced by cloud depth but also has no relation with the cloud base.A probable reason for this could be that SWCRFis highly dependent on cloud optical depth,which is positively correlated with cloud depth.Also noteworthy is that the spatial distribution of SWCRFand CBH exhibits an obvious negative correlation.As shown inFig.7c
,the SWCRFis low in northwest China where high clouds always occur.In contrast,the SWCRFin southeast China is high,which is attributed to the low cloud base in this region.A possible reason may be that low clouds tend to increase the multiple scattering and absorption of solar radiation between the clouds and the surface,which enhances the solar radiation absorbed by the cloud,thus,resulting in a marked increase in the SWCRF.This result demonstrates that the height of the cloud base significantly contributes to the estimate of the SWCRF.By comparison,the frequencies of the SWCRFas a function of latitude are consistent with the height of cloud base,which increases first and then decreases as the latitude increases.This further highlights the importance of the cloud base in modulating SWCRF.3.4.Correlation analyses between SWCRF and CBH
To further examine the relationship between the CBH and SWCRF,the SWCRF,SWCRF,and SWCRFare calculated by differentiating between the various vertical distribution patterns of COD,which has already been clarified inTable 1
andFig.1
.Figure 8
shows the comparison of the CBH and SWCRF at the surface,top-of-atmosphere,and in the atmosphere.As expected,the SWCRFnegatively correlated with cloud base,while the SWCRFand SWCRFhave no relation to cloud base.Under Scenarios 2 and 3,the correlation of SWCRFwith the height of cloud base is strong,with the R values as high as 0.76.However,under Scenario 0,the relationship between SWCRFestimates and cloud base is weak,since it does not consider the cloud base at all.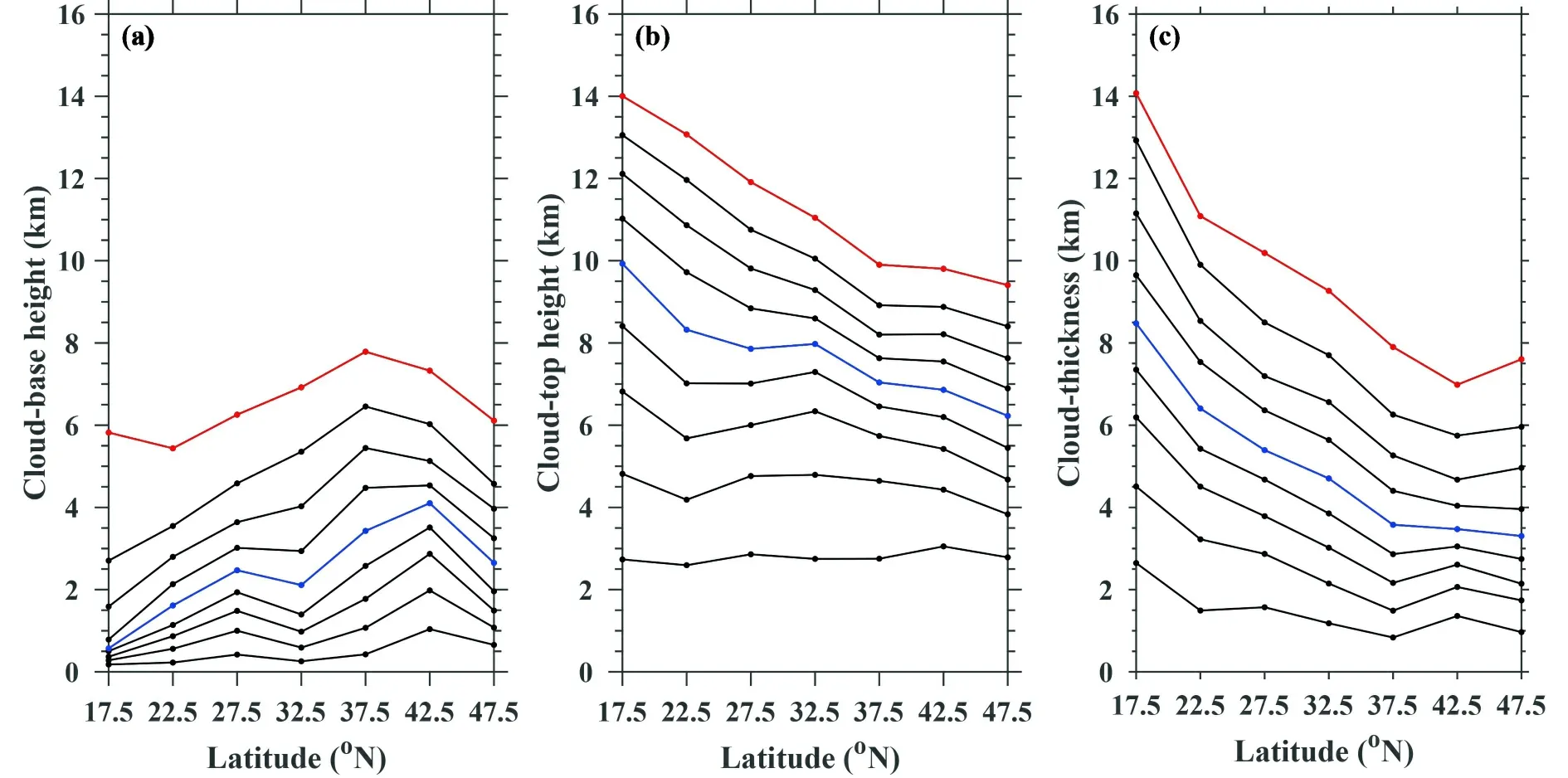
Fig.4.Evolution,as a function of latitude and percentile,for (a) cloud-base height,(b) cloud-top height,and (c) cloud thickness over China in the summers during the period from 2010 to 2018.The 10th−90th percentiles in 10 percentile increments are shown,with the 50th and 90 th percentiles highlighted in blue and red,respectively.
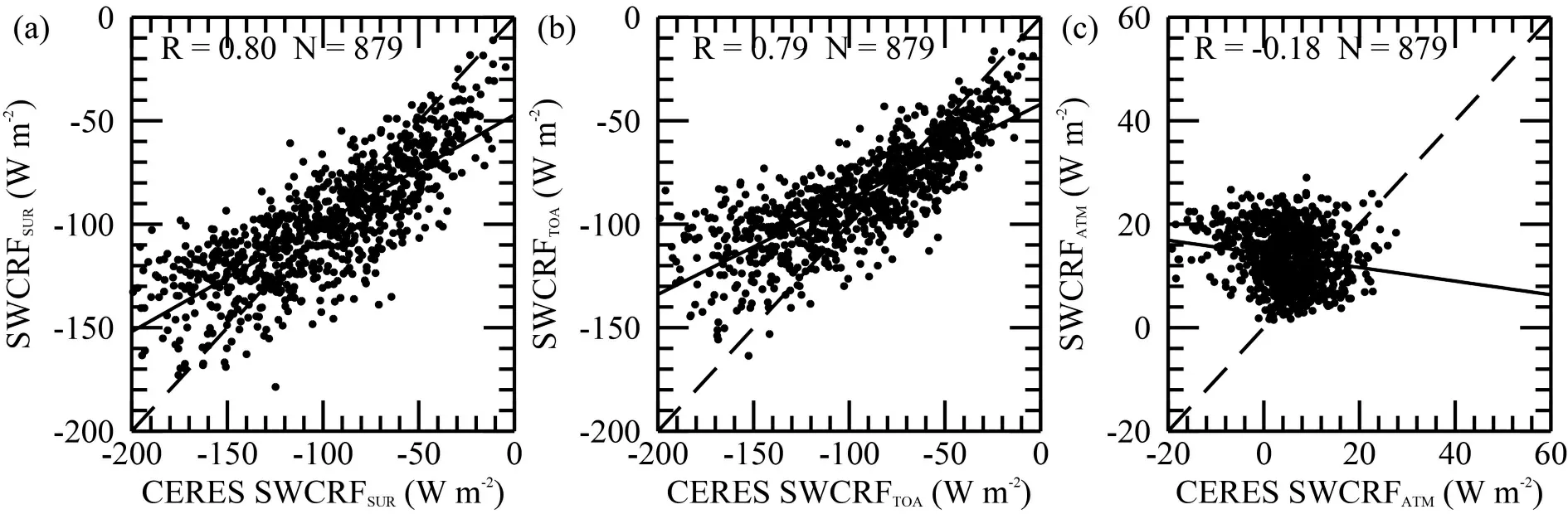
Fig.5.Scatterplots of (a) SWCRFSUR,(b) SWCRFTOA,and (c) SWCRFATM using the CBH from radiosonde measurement,MODIS-observed CTH,and ancillary cloud parameters under Scenario 2 versus that from the CERES product in China.The regression lines of estimated SWCRFs against CERES-derived SWCRFs are given as well.Note that all samples are limited to the period in summer in 2013.
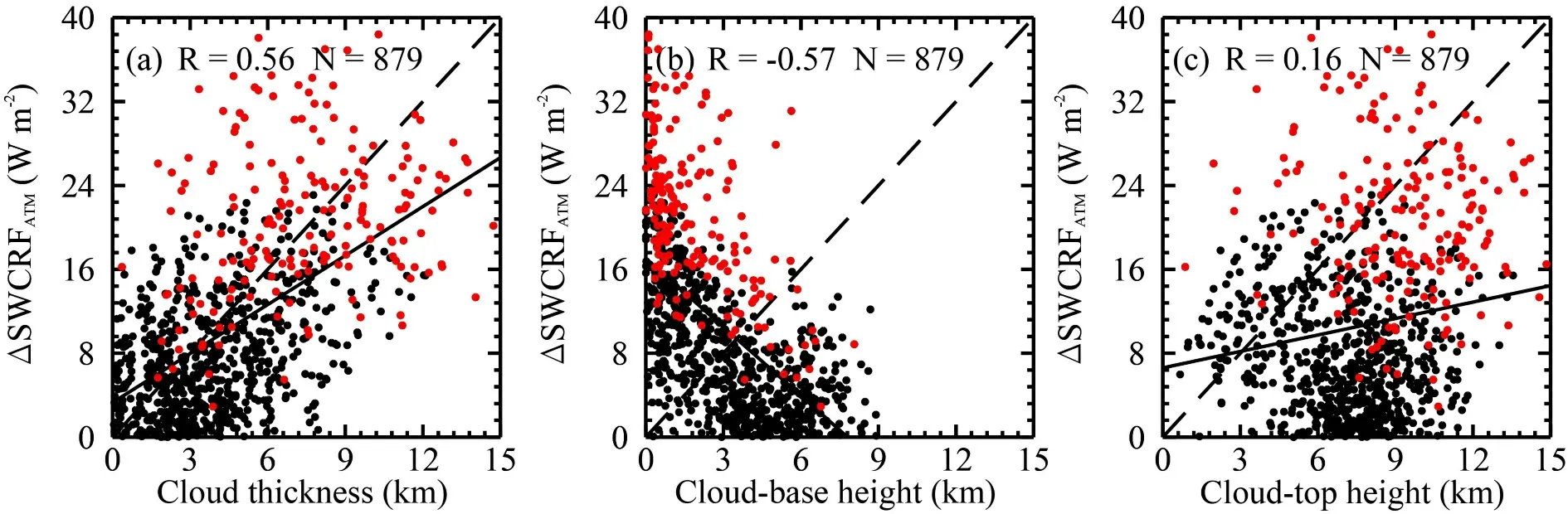
Fig.6.The difference between the CERES-derived SWCRFATM and the simulated SWCRFATM (ΔSWCRFATM) shown as a function of (a) cloud thickness,(b) cloud-base height,and (c) cloud-top height.The red points represent those samples with negative SWCRFATM from CERES.
3.5.Impact of CBH on SWCRF
In this section,we will perform a quantitative analysis to deduce how the SWCRFis dependent on cloud base.The SWCRF estimates,under different vertical profile scenarios of COD,are shown inFig.9
.Overall,the estimates of SWCRFdo not differ with the vertical distribution of COD (Fig.9a
).On average,the relative deviations of the SWCRFwith (Scenarios 1−3) and without (Scenario 0)considering cloud bottom is very small (only 0.32%),which indicates that the impact of cloud base on the SWCRFcan be ignored.This result is consistent with previous studies pointing out that the SWCRF at the surface is independent of the cloud bottom height (e.g.,George et al.,2018
).Similar to the SWCRF,the error in the SWCRFestimates considering no cloud bottom is not as obvious(Fig.9b
).However,it is inferred that the SWCRFtends to be overestimated if the cloud base is not considered in the estimation of cloud forcing,especially under Scenario 1.The relative deviations of the SWCRFunder Scenario 1 from that under Scenario 0 is nearly 6.1%,which demonstrates that an accurate cloud base is more essential to the SWCRFthan to the SWCRF.In stark contrast to the SWCRFand the SWCRF,the magnitudes of estimated SWCRFunder different profile scenarios of COD differ greatly(Fig.9c
).Given the lack of consideration of an accurately described cloud bottom,the SWCRFis expected to be underestimated.The possible reason is that the true cloud bottom would be overestimated if the cloud base is not considered in the calculation of the SWCRF,which would reduce the multiple scattering and absorption of solar radiation between the surface and cloud layer,ultimately resulting in an underestimate of the SWCRF.
Fig.7.Spatial distributions of (a) SWCRFSUR,(b) SWCRFTOA,and (c)SWCRFATM under Scenario 2 in China in summer for the period from 2010 to 2018.The blue bars on the right-hand side represent their corresponding frequency of SWCRF in various latitudes.
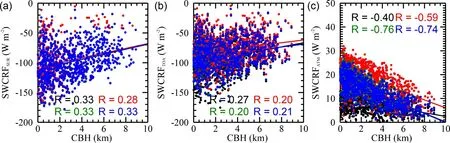
Fig.8.The (a) SWCRFSUR,(b) SWCRFTOA,and (c) SWCRFATM shown as a function of CBH under four vertical configuration scenarios of cloud by assuming the vertical profile of COD:Scenario 0 (black),Scenario 1 (red),Scenario 2(green),and Scenario 3 (blue).
The absolute (relative) discrepancy of the SWCRFbetween Scenario 0 and Scenarios 1−3 reaches up to 9.61(57%),5.43 (42%),and 4.82 (40%) W m,suggesting that the influence of cloud base on the SWCRFestimate under Scenario 1 is much larger compared to that under Scenario 2 and 3.This could be likely associated with the multiple scattering and absorption of solar radiation.With the assumption of a two-point COD vertical distribution,the multiple scattering and absorption of solar radiation become strongest,which allows more solar radiation to be absorbed by the clouds,resulting in a commensurate increase of the SWCRFOverall,the SWCRFestimates without using cloud base as input are considerably lower than those that use the cloud base,indicating the importance of using an in situ observed cloud base for an accurate calculation of the SWCRF.
3.6.Sensitivity of SWCRF to CBH and SZA
Provided that the solar zenith angle (SZA) can greatly modulate the total solar radiation that is available to interact with cloud layers,this subsection will elaborate on the sensitivity of the SWCRF to CBH and SZA in an attempt to further quantify how the SWCRF changes with the cloud base.As shown inFigs.10a
−c
,the SWCRFestimates are nearly unaffected by increases in the height of cloud base,irrespective of SZA and the vertical profile of COD.This indicates that the calculation of SWCRFdoes not change appreciably with the cloud base and/or the SZA,which has been well documented in previous studies.For example,Meloni et al.(2005)
reported on the modest dependency of the shortwave radiative forcing on the vertical profile of the cloud.The reasons behind this may be that the total COD and other cloud properties do not change much,and thus the capability for the cloud to scatter and absorb solar radiation is kept nearly constant.The sensitivity of the SWCRFto CBH and the SZA exhibits similar behavior as those for the SWCRF(Figs.10d
−f
).The sensitivity of the SWCRFto both cloud base and the SZA is weak.As the cloud base increases,the magnitude of SWCRFtends to increase.This may be related to the expectation that a higher cloud base corresponds to a larger COD for the top of the cloud,which enhances the scattering of the solar radiation,and thus results in an increased SWCRF at the top of the atmosphere.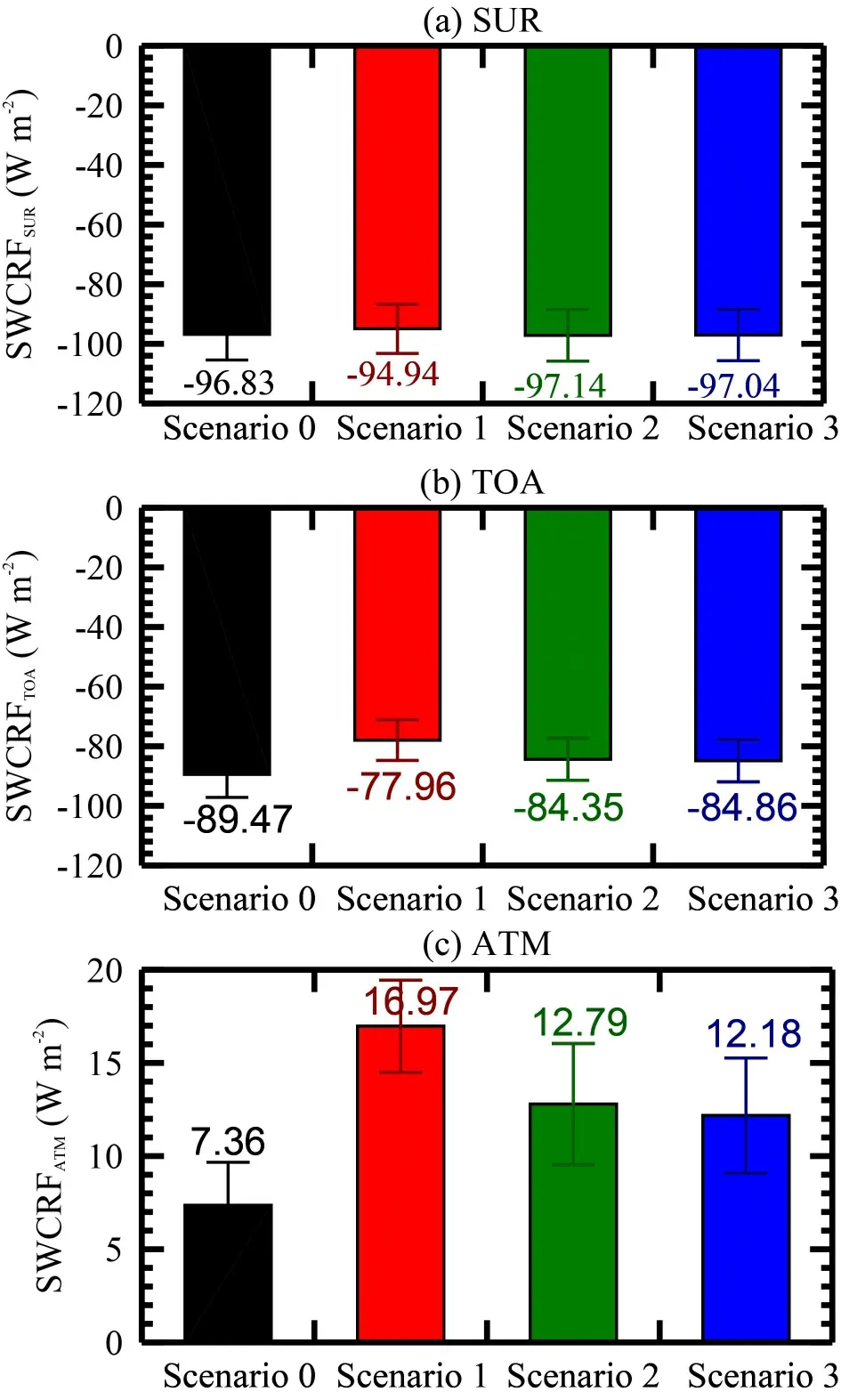
Fig.9.Comparison of the nationwide mean summertime values for (a) SWCRFSUR,(b) SWCRFTOA,and (c)SWCRFATM in China during the period from 2010 to 2018 under four vertical configuration scenarios of cloud by assuming the vertical profile of COD:Scenario 0 (black),Scenario 1 (red),Scenario 2 (green),and Scenario 3 (blue).
In sharp contrast to the SWCRFand SWCRF,the calculated SWCRFis found to be sensitive to both cloud base and SZA,and the slope or sensitivity becomes much stronger (Figs.10g
−i
).Interestingly,the magnitude of the SWCRFtends to decrease with a commensurate increase of cloud base in a monotonic scaling way.Also noteworthy is that the scaling rate of the SWCRFwith cloud base differs greatly according to the scenario.The sensitivity under Scenario 1 and Scenario 3 is much larger than Scenario 2.More striking is that the SZA not only changes the slope,but also the absolute magnitude of SWCRF.For instance,the magnitude of SWCRFunder Scenario 1 is found to decline from 17−23 W mat SZA of 0° (Fig.9g
) to −7−2 W mat SZA of 60° (Fig.9i
)as the Δhincreases from 0.5 km to 5.0 km,which indicates that the SWCRFdecreases along with the increase of SZA.Besides,this suggests that the largest discrepancy of SWCRFunder Scenario 1 preferentially occurs under small SZA conditions,which generally corresponds to late morning,noon,or early afternoon,which is roughly consistent with the results mentioned in section 3.5.By comparison,the largest discrepancy of the SWCRFunder Scenario 2 preferentially occurs under large SZA conditions,which generally corresponds to early morning and late afternoon.We also notice that the increases in SZA are closely associated with a decreased SWCRFthat is estimated with CBH as input,further illustrating the important role of cloud base.
Fig.10.SWCRFSUR (a−c),SWCRFTOA (d−f),and SWCRFATM (g−i) shown as a function of the increase in CBH (Δhb) under four vertical configuration scenarios of cloud by assuming the vertical profile of the COD:Scenario 0 (black),Scenario 1(red),Scenario 2 (green),and Scenario 3 (blue).
4.Summary and conclusions
In this present study,a long-term record of the summertime SWCRF at the surface,at the top of the atmosphere,and in the atmosphere during the period from 2010 to 2018 has been generated using the CBH estimated by radiosonde measurements and the CTH and cloud properties derived from MODIS/Aqua product.To our best knowledge,this work is the first to take the in situ measured cloud base into account when calculating the SWCRF.Overall,the CBHs show significant spatial variability that is characterized by a“northwest-high-southeast-low” pattern.Compared with the CBH,the CTH has a different spatial pattern.Consequently,the SWCRFfollows the spatial pattern of CBH,which suggests that the cloud bottom is the main factor in modulating the shortwave cloud forcing in the atmosphere.
Overall,there are good correlations between the simulated and the CERES-derived SWCRFs.However,an obvious disagreement occurs between the simulated and CERES-derived SWCRFespecially for thick clouds with low cloud bottoms.Also,a series of experiments have been done by assuming two kinds of vertical profiles of COD,Scenario 0 and Scenarios 1−3.The former assumption features only CTH and cloud properties from MODIS as input,and the latter combines both CTH and cloud properties and CBH.
Comparison analyses further suggest that a large discrepancy exists in SWCRFbetween Scenario 0 and Scenarios 1−3.Meanwhile,Scenario 1 produces the largest uncertainties of the SWCRF.By comparison,no dramatic difference is observed for the estimate of the SWCRFand SWCRF,under the different scenarios concerning the vertical profiles of the COD.Given the nature of the COD assumed as a two-point distribution under Scenario 1,it is inferred that adequate consideration of the cloud base,would lead to much more realistic estimates of cloud forcing in the atmosphere.Furthermore,the sensitivity analyses also corroborate the findings mentioned above,Scenario 1 produces much more realistic cloud forcing compared with those without consideration of cloud layers in the vertical.As for Scenario 2,the influence of the cloud base on the cloud forcing is largest under large SZA conditions.Therefore,we argue that the impact of CBH depends upon an accurate estimate of the SWCRF,especially under Scenario 1,at the time period from late morning through early afternoon when the SZA is relatively small,or under Scenario 2 for the early morning and late afternoon.
Nevertheless,we have to emphasize that our study makes relatively simple assumptions for the vertical profiles of the COD,which inevitably impairs our ability to accurately estimate the cloud forcings.Our understanding and accurate computation of cloud forcing will be greatly improved with the inclusion of additional instrumentation that can resolve the vertical structure of clouds,which will result in more realistic forcing caused by the changing clouds under global warming.Besides,MODIS/Aqua only provides a single snapshot of the clouds,which makes it impossible to characterize the diurnal cycles of cloud properties (e.g.,the cloud fraction,COD,and cloud effective radius) and ultimately cloud radiative effect.Improvement in this regard is worthy of separate analysis and should be based on deriving cloud properties from geostationary satellites,like Himawari-8 and Fengyun-4.
.We acknowledge the support from the National Key R&D Program of China under Grants Nos.2017YFC1501401 and 2017YFC0212803,the National Natural Science Foundation under Grant No.41771399,and the Chinese Academy of Meteorological Sciences under Grant No.2018Y014.Also,we are grateful to NASA for granting access to the level-3 cloud products from MODIS/Aqua.Last but not least,special thanks go to the National Meteorological Information Center,China Meteorological Administration for generously providing the radiosonde datasets used here (https://data.cma.cn/en
). Advances in Atmospheric Sciences2021年9期
Advances in Atmospheric Sciences2021年9期
- Advances in Atmospheric Sciences的其它文章
- A New Semi-Lagrangian Finite Volume Advection Scheme Combines the Best of Both Worlds
- Re-examining Tropical Cyclone Fullness Using Aircraft Reconnaissance Data
- Response of Growing Season Gross Primary Production to El Niño in Different Phases of the Pacific Decadal Oscillation over Eastern China Based on Bayesian Model Averaging
- The Initial Errors in the Tropical Indian Ocean that Can Induce a Significant “Spring Predictability Barrier” for La Niña Events and Their Implication for Targeted Observations
- Seasonal Variations of CH4 Emissions in the Yangtze River Delta Region of China Are Driven by Agricultural Activities
- Melt Pond Scheme Parameter Estimation Using an Adjoint Model
