地质灾害监测数据综合处理与分析

崔芳姿，吴 斌，史学磊，范振林，任 涛

（1.中国地质调查局水文地质环境地质调查中心,河北 保定 071051）

对于地质灾害防治来说,监测并不是目的,通过大量监测数据预测灾害变形趋势乃至预报灾害发生的时间,提前做出决策,做到防患于未然才是监测的最终目标。换句话说,即使是建立了先进有效的监测系统,取得了丰富的监测数据,而不具备对数据的综合分析和对灾害的预测预报能力,灾难同样可能发生[1-3]。因此,如何结合灾体分析监测数据,预测灾害变形趋势,预报其失稳时间并提出合理的对策措施,是监测预警的核心内容[4-6]。

由于地质灾害的复杂性,其预测预报技术是一项世界性的技术难题。尽管各种各样的预报理论、模型不断涌现,但应用成功的实例极为少见。预报成功的例证基本上是在连续监测,并对各种地质现象进行综合分析的基础上做出的,其成功率取决于技术人员对地质灾害的认识水平、经验和态度,具有很大的不确定性。另外,地质灾害监测数据存在误差以及由数据传输或设备问题导致的数据缺失,而国内外大多地质灾害监测预警系统没有对监测数据进行预处理[7-9]。因此,研究和提高地质灾害监测数据预处理、监测数据综合分析（特别是与致灾地质作用的结合分析）和预测预报能力是十分必要的,也是极为紧迫的[10-11]。

本文提出了一套地质灾害监测数据综合处理与分析技术,并设计了地质灾害数据信息化管理系统。基于数据库提供的统一数据模型和数据服务,结合巫山县地质灾害监测预警示范站地质灾害业务信息和地质灾害监测数据,本文建立了一套统一的数据标准规范,实现了灾害点、监测点、监测设备管理的数据综合处理与分析服务,并通过该服务建立和完善了监测数据预处理方法、监测数据综合分析方法和预警预报方法,进一步提高了地质灾害监测预警信息的综合处理能力,为地质监测管理决策人员提供辅助支持,保障地质灾害监测预警工作顺利进行。

1 数据综合处理与分析服务综述

数据综合处理与分析服务构建于统一的地质灾害监测数据和业务应用服务之上,基于统一的地质灾害监测数据,首先将数据传输到数据库,并对数据和统计量进行数据质量分析、相关性分析、异常值剔除、数据等距化、数据平滑等一系列处理；再绘制位移矢量图、位移/速率-时间曲线,并利用切线角法进行预警预报,如图1所示。数据综合处理与分析服务能进一步提高地质灾害监测预警信息的综合处理能力,为地质监测管理决策人员提供辅助支持。

图1 数据综合处理与分析服务流程图

基于数据综合处理与分析服务,本文设计了一套地质灾害数据信息化管理系统,如图2所示,采用B/S技术架构,支持IE、360、Google Chrome等浏览器,总体包括数据采集层、地质灾害监测数据库、基础管理、地质灾害监测数据综合处理与分析服务以及数据交换等部分,还包括安全保障体系、维护支撑体系、数据标准规范体系等外围支持。系统基于巫山县地质灾害监测预警示范站的地质灾害信息,通过采集巫山县地质灾害监测预警示范站地质灾害业务信息和地质灾害监测数据,构建统一的地质灾害数据库；利用数据库提供的统一数据模型和数据服务,构建地质灾害数据信息化管理系统,为地质灾害监测预警业务提供应用服务；通过数据接口和数据交换,为其他政务系统提供各类信息服务。

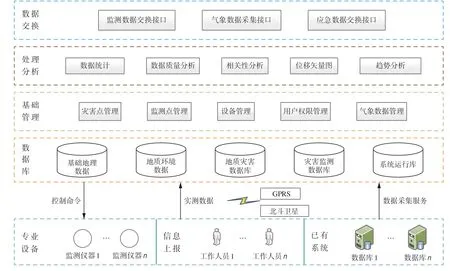
图2 系统技术架构图

2 关键技术

2.1 监测数据预处理

监测数据预处理包括异常数据剔除、差补与平滑等内容。

2.1.1 异常数据剔除

在科学研究实验中,经常会出现因仪器故障或读数错误而出现的误差。对于大量数据可疑值的判别,常用的统计判别方法为拉依达检验（3σ准则）。该准则是以99.73%的置信度,根据随机误差正态分布理论判断是否存在可疑值。若|xi-x|＞3σ,则应舍去xi,否则应保留xi；可用max(abs(xi-mean(xi)))≥3std(xi)条件是否满足来实现,其中abs()是绝对值函数,max()是最大值函数,std()是标准差函数。

2.1.2 数据等距化（差补）

由于仪器数据有时存在缺失或两端数据的数据间隔不同,不方便进行数据分析,需对数据进行等距化,将数据转化为间隔相等的数据。

本文采用三次样条插值法进行等距化处理,即对数据进行样条函数曲线拟合得到一条曲线,再由拟合后的曲线计算得出其他任意时刻的值。设有两个传感器A和B,分别以不同的频率对目标进行采样测量,各传感器可均匀采样,也可非均匀采样。每个传感器在采样时刻ti的测量值记为(ti,yi),其中yi为向量,这样每个传感器均可得到一组测量值。由于传感器的采样周期不同,各传感器获得数据的时间值不尽相同,若直接进行融合,则可能会因时间差而使融合结果失去意义,反而不如单个传感器的融合精度高,因此在进行数据融合前,必须将不同时刻的测量数据对准到同一时间点上。

设传感器A在某一时间段[a,b]内对目标进行了n+1次测量,将整个时间区间按采样时刻划分为a=t0＜t1＜…＜tn=b,给定的时刻点ti对应的观测值为f(ti)=yi,i=0,1,…,n,构造一个三次样条插值函数s(x),使其满足下列条件:①s(ti)=yi,i=0,1,…,n；②s(x)在每个小区间[ti,ti+1]上是一个三次多项式,i=0,1,…,n-1；③s(x)在[a,b]上具有二阶连续导数。

基于最小二乘法的样条函数拟合是在样条函数空间内找出f(t)关于范数的最佳逼近,即找到s*(t),使

三次样条插值函数的构造过程为:记mi=s'(ti),i=0,1,2,…,n在每个小区间[ti,ti+1],i=0,1,2,…,n-1上,利用Hermite插值公式写出三次样条插值函数的计算公式,即

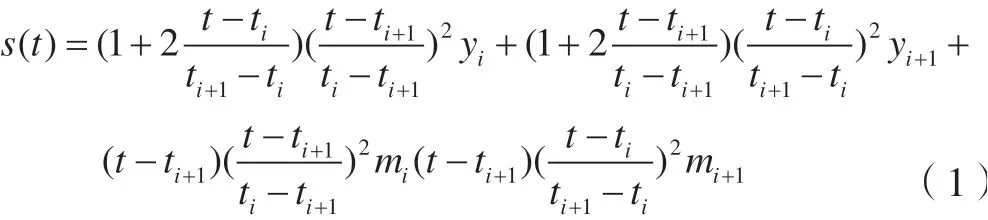
利用s"(ti-)=s"(ti+),i=0,1,2,…,n-1,并附加边界条件s"(t0)=s"(tn)=0,可得方程组:

式中,a0=1；

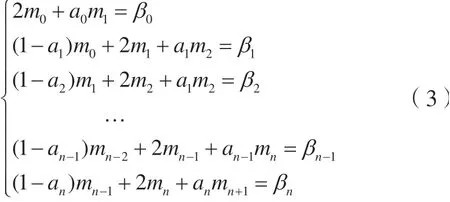
方程组系数矩阵为三角矩阵,其行列式不为0,所有方程组的解存在且唯一, 对方程组求解,即可得到递推公式:

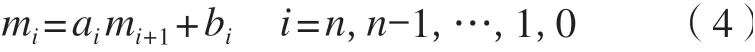
利用公式求出ai、bi,i=1,2,…,n,令mn+1=0,求出mn、mn-1、…、m0,将参数ti、yi、mi,i=1,2,…,n代入s(x)中即可求得三次样条插值函数。

经过样条插值拟合,可以得到一条平滑曲线,从而由其求得传感器在任意时刻的值；再与其他传感器进行时间对准,根据采样时刻,从该条曲线中取出相应时刻的测量值。

2.1.3 数据平滑

仪器观测数据存在随机误差（波动）,数据趋势分析时需摒弃误差,找到数据真正的变化趋势,因此需进行数据平滑处理。对于数据长度较小的数据,采用整体平滑处理,即三阶一般多项式拟合平滑方法；对于长期监测数据,则采用窗口的移动方法,分时段进行平滑处理。

对于给定的一组数据(xi,yi),i=0,1,…,m要求在函数类ψ={ψ0,ψ1,…,ψn}中找一个函数y=S*(x),使误差平方和最小,即

式中,S(x)=a0ψ0+a1ψ1+…+anψn,n＜m。

这就是一般的最小二乘逼近,即曲线拟合的最小二乘法。为了使问题的提法更有一般性,通常把最小二乘中的考虑为加权平方和,即

这里w(x)≥0为[a,b]上的权函数,表示不同点(xi,f(xi))处的数据比重。利用最小二乘法求拟合曲线的问题,就是在S(x)中求函数y=S*(xi),使式（6）取得最小。将其转化为求多元函数I(a0,a1,…,an)=问题。根据多元函数极值的必要条件,则有:

若记

则可改写为:

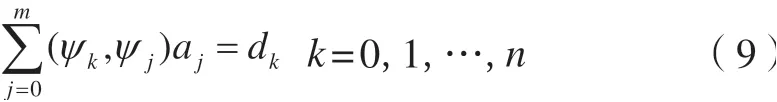
将其写成矩阵Ga=d,其中a=(a0,a1,…,an)T,d=(d0,d1,…,dn)T,则有:

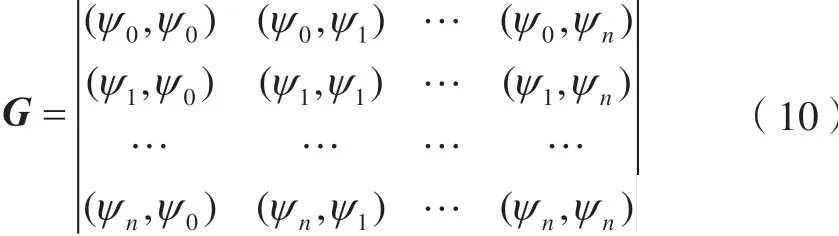
由于ψ0,ψ1,…,ψn线性无关,因此|G|≠0,式（6）存在唯一解,ak=ak*,k=0,1,…,n,从而得到函数f(x)的最小二乘解为:

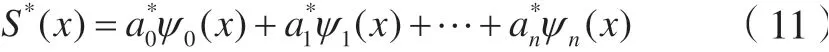
可以证明这样得到的S*(x),对任何形如式（1）的S(x),均有:

2.2 监测数据综合分析

2.2.1 相关性分析

相关性分析可用来验证两个变量间的线性关系,通过相关系数可反映两个变量是否呈线性关系、线性关系强弱以及是正相关还是负相关。最简单最常用的相关系数计算方法为积差法,即利用两个变量的协方差与二者标准差的乘积之比来表示,计算公式为:

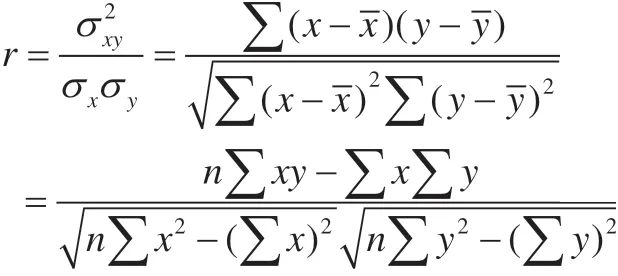
相关性系数介于-l～1之间,若r接近0,则两个变量没有线性关系；若r接近-l或1,则说明两个变量线性相关性很强；r为正,表示正相关,r为负,表示负相关。

2.2.2 变形趋势分析

数据综合处理与分析服务不仅针对原始监测数据,还针对原始数据的统计量。各个统计量的计算规则为:累计变形量,即当前值-初始值；平均变形速率,即（当前值-初始值）/月；上半年变形增量,即当前值-上半年初始值；上半年变形速率,即上半年变形增量/6；上半年数据中误差,即sqrt(((dx12+dx22…)-(dx1+dx2)2/n)/(n-1))；变形方向,即dx累计变形量和dy累计变形量计算。

2.3 预警预报方法

2.3.1 变形趋势预测方法

位移矢量图（平面图）反映了变形监测点随时间在空间上的变化情况,主要表示变形量和变形方向,即二维空间上的x方向累计变形和y方向累计变形,能直观显示滑坡整体的变形态势。

2.3.2 切线角法

对于某个滑坡来说,等速变形阶段的位移速率v为一个恒定值,则可通过累计位移S/v的办法将S-t曲线的纵坐标变换为与横坐标相同的时间量纲。定义S(i)为某一单位时间段（一般采用一个监测周期,如1 天、1 周等）内的斜坡累计位移量,v为等速变形阶段的位移速率,T(i)为变换后与时间相同量纲的纵坐标值。

由T-t曲线（图3）可得到改进的切线角的表达式为:

图3 滑坡位移/速率—时间曲线

3 实例开发应用

本文基于数据综合处理与分析技术设计了一套地质灾害数据信息化管理系统,主要包括基础地理信息模块、地灾监测信息“一张图”模块、灾害信息管理模块、地灾专业监测模块、数据综合处理与分析模块和系统维护管理模块,如图4所示。

图4 系统功能结构图

通过综合处理与分析服务可以判断监测数据是否可靠,调整监测重心,预测边坡的失稳时间,掌握宏观变形特征,判断所处变形阶段和稳定性现状,进而研判未来一段时间的地质灾害变形发展趋势。

1）监测数据预处理方法应用。将斜坡变形演化阶段应变（位移）—时间曲线的三阶段过程视为滑坡预测预报的基本标准:第I阶段为初始变形阶段,又称减速变形阶段,岩土体变形以减速发展,变形曲线斜率逐渐减小；第Ⅱ阶段为等速变形阶段,又称稳定变形阶段,岩土体变形大致以等速发展,变形曲线近似一条倾斜直线,应变速率大体不变；第Ⅲ阶段为加速变形阶段,岩土体变形速率迅速增加,至岩土体破坏。

通过异常数据剔除、数据等距化与数据平滑等预处理,提高了地质灾害监测数据的可用性,形成了多参数历史曲线图。当坡体已进入加速蠕变阶段和临滑阶段时,可根据多参数历史曲线图上位移随时间增长速率的变化来预测边坡的失稳时间。

2）监测数据综合分析方法应用。通过变形趋势分析可统计监测运行以来各监测点的累计水平位移量、累计垂直位移量、累计水平变形速率、累计垂直变形速率、上半年度水平位移增量、上半年度垂直位移增量、上半年度水平变形速率、上半年度垂直变形速率、上半年度水平位移中误差、上半年度垂直位移中误差和变形方向。

利用滑坡变形量和变形速度能调整滑坡监测频次。对于多年监测缓慢变形或基本不变形的灾害点应降低专业监测频次甚至改为群测群防监测,以减少监测工作投入和数据处理与分析的工作量。通过变形方向可以判断各监测点的变形方向与主滑方向是否一致。将中误差与技术规范中要求的监测数据误差进行对比分析,实测误差是否在容许范围之内,以判断数据的可靠性。

3）预警预报方法应用。位移矢量图可反映各监测点的变形量、变形方向、变形发生部位,各监测点上变形差异,属于整体变形还是局部变形以及宏观变形特征等。通过曲线可判断各监测点变形的主要发生时间；综合变形特征与宏观巡查分析,可判断所处变形阶段和稳定性现状,从而研判未来一段时间的地质灾害变形发展趋势。

当切线角α≤45°时,斜坡变形处于等速变形阶段,进行蓝色预警；当切线角45°＜α＜80°时,斜坡变形进入初加速变形阶段,进行黄色预警；当切线角80°≤α＜85°时,斜坡变形进入中加速变形阶段,进行橙色预警；当切线角α≥85°时,斜坡变形进入加加速变形（临滑）阶段,进行红色预警；当切线角α≈89°时,滑坡进入临滑状态,应发布临滑警报,如表1所示。

表1 滑坡变形预警级别划分

4 结 语

地质灾害监测数据综合处理与分析服务是地质灾害数据信息化管理系统的关键,通过异常值剔除、数据等距化、平滑、绘制位移—时间曲线等处理,能大大提高地质灾害监测数据的可用性,提高地质灾害监测预警信息的综合处理能力。通过数据综合处理与分析服务,建立和完善监测数据预处理方法、监测数据综合分析方法以及预警预报方法,结合变形特征判断所处的变形阶段和稳定性现状,进而研判未来一段时间的地质灾害变形发展趋势。利用数据预处理方法、综合分析方法和预警模型解决了地质灾害预警工作中的数据缺失、数据质量差、预警模型缺失等问题,为地质灾害预警工作和防灾减灾工作提供了技术支撑,对于防治决策服务成功实施和地质调查工作顺利进行具有重要意义。