基于卷积神经网络的冲击地压微震定位法

郭松林，王朝晖

（黑龙江科技大学，黑龙江哈尔滨，150000）

1 绪论

冲击地压微震是指煤岩体在复杂外界条件下发生结构破裂，产生微震信号。这些微震信号经常被用来研究和评价煤岩体稳定性[1-2]。现今用于矿下的微震监测技术包含多方面内容，其中震源定位被认为是冲击地压研究领域中最核心的研究方向[3]。

本文利用卷积神经网络进行冲击地压微震定位，文中把监测区域划分为5*5的区域，用二维数组[x，y]来表示（其中x，y取值为1-5的整数），模型采用有监督学习，所有的震动事件均将通过卷积神经网络模型对应到图中每一个区域中，将定位问题转换为分类问题，这种方法保持了卷积神经网络对二维数据处理的优势，能够达到较高的定位准确度。

1.1 样本处理

为了确保训练模型最终能够达到好的定位效果，必须对实验事件进行合适挑选：

（1）用于模型训练的的微震事件，必须在取样时间段内是完整可靠的；

（2）实验所选的每个记录时间以震动触发时为中点，前后各取5ms。将（-5ms，5ms）定为一个震动事件的时间域。

经过以上筛选和校正后，共选取了240个微震事件，每一个事件均由两个维度（A和B）所采集的震动信号构成。震动信号如下图所示。

图1 震动信号示例A

图2 震动信号示例B

图中横轴为震动采集时间，取值范围（-5ms，5ms）；纵轴为电压信号，表示震动幅值大小，取值范围（-6V，6V）。

1.2 短时傅里叶变换

本文利用短时傅里叶变将一维数据转换为二维数据。冲击地压微震信号是一种不平稳的震动信号，对这种非平稳信号f(t)，采用窗函数α作短时 Fourier 变换，计算公式如下：

其中ε表示某一待分析时间点，s表示频率，α(t−ε)表示以ε为中心的分析窗。

下图分别是对某一信号样本的短时傅里叶变换图，对每个样本的A、B两个维度分别进行短时傅里叶变换。

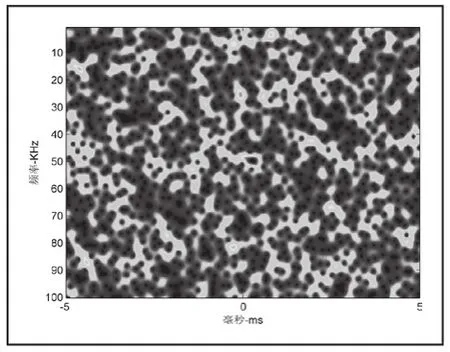
图3 信号1A变换图

图4 信号1B变换图

2 定位方法与网络结构

2.1 卷积神经网络

本文搭建的网络模型，如图5所示。整个网络结构包含了4个卷积层、4个池化层以及2个全连接层。网络的输入层采用512*512*2的尺寸。最终到达第四个池化层后输出32*32*128的尺寸。之后经过全连接层计算，由于研究区域被划分为25个区间，所以输出采用25的模型尺寸。

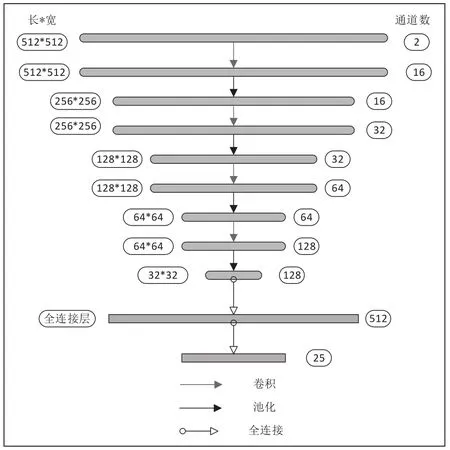
图5 网络结构

2.2 卷积层

卷积层主要包括特征图以及卷积核。具体的卷积操作如图6。当卷积核卷积位置超出特征图有效位区域时，做填充或其他操作。然后激活函数对卷积后的值做激活操作。得到卷积层最终的输出。

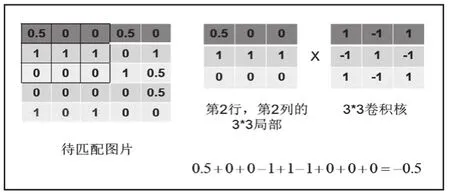
图6 卷积层的运算过程示意图

2.3 池化层

池化层可以用来减小特征图的大小，减少模型计算时间，对上一层的特征进行数据压缩计算。池化层分为最大池化层和平均池化层，在本文中所有池化层的池化运算步长为2，均采用最大池化。池化层的操作过程如图7。

图7 池化层的池化过程示意图

2.4 损失函数

由于定位区域被划分为5*5的结构，每个震动对应的二维坐标[x，y]表示该震动的期望值，所以本文使用了二维交叉熵函数来度量模型损失值的大小。

一维交叉熵损失函数：

式中：N——训练的总样本数

y——期望输出，即有监督训练的标签；

o——实际输出，即经过模型运算给出的结果；

Q——损失值，表示期望值与训练值之间的误差大小。

本文使用的二维交叉熵损失定义为：

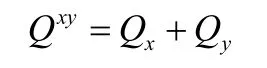
其中Qx，Qy分别表示两个维度上的交叉熵损失值。

3 实验及分析

3.1 实验环境及配置

本次实验建立在Window10，64位的操作系统之上，使用Tensorflow2.0作为深度学习框架，软件编程使用以Python为基础的卷积神经网络函数库。

实验共有数据240组，这240组数据中的200组用于模型训练，剩余40组用于检测模型的准确率。

3.2 模型训练过程

设定学习率lr为0.001，迭代数epoch为500，批大小batch为40，将200个数据进行5批训练，计算每一批次的损失值loss累加计算均值，这样就更精确地计算loss。

初始化网络参数，开始训练网络，通过迭代最小化交叉熵的损失loss，优化网络连接权，提高模型准确率。

每次训练后保存卷积神经网络模型的参数，将损失值和准确率实时记录下来。

3.3 结果分析

训练完成后，保存绘制成的变化曲线用来观察模型定位效果。训练中的损失loss以及准确率acc的变化的曲线分别如图8、9所示。

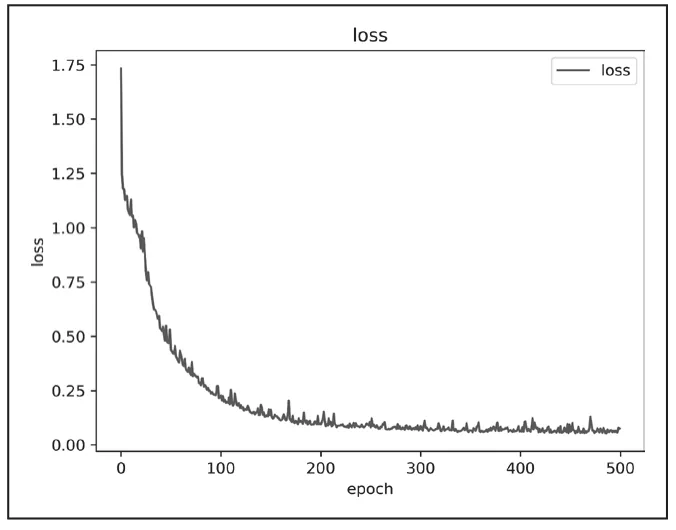
图8 模型损失函数变化图

图9 模型准确率变化图

通过损失函数和准确率的变化曲线可以看到，在完成500次迭代后，损失函数值为0.0753，准确率达到了97.5%。

表1 定位法准确率对比

本实验采用TDOA时差定位法[4]进行对照分析，将240组数据进行定位计算，把计算位置与实际震源位置处于同一区域内的事件标记为准确定位。比较两种定位结果后可以发现，时差定位法的准确率为92.5%，低于本文采用的卷积神经网络定位法的准确率97.5%。

4 结束语

本文针对冲击地压微震定位任务提出了一种通过卷积神经网络进行定位的方法，并采用短时傅里叶变换将处理后数据直接代入模型，该定位法利用了卷积神经网络强大的二维数据处理方法和优秀的特征提取能力。通过实验及结果分析表明，该方法在微震定位中能取得较好的定位效果，定位准确率是优于TDOA时差定位法的。