一种关于驾游路线规划的分布均匀度自适应蚁群算法
宋明杰,吴宇航
(1.华北理工大学 理学院,河北 唐山 063210;2.华北理工大学 教务处,河北 唐山 063210;3.河北省数据科学与应用重点实验室,河北 唐山 063210)
0 引言
自驾游是当今热门的出行方式,是以旅行人自行驾驶交通工具,有组织、有计划的按照既定方案进行旅行[1],其在旅游目的地的选择、到达与停留时间以及食宿安排上都有很大的自主性,与传统的参团方式相比更有独特魅力。如何合理的规划旅行路线,在旅行体验和经济开支上进行合理平衡,成为广大自驾游爱好者需要考虑的重要因素[2],因此如何规划旅行路线成为了一个现实性的研究课题。
蚁群算法[3]是近年来出现的一种新型的模拟进化算法。它充分利用了蚁群搜索食物的过程与旅行商问题(TSP)[4]之间的相似性。蚁群算法在求解复杂优化问题方面具有很大的优越性,而引入分布均匀度后的自适应蚁群算法在加速收敛和防止早熟停滞现象之间取得很好的平衡,更适合于求解大规模的TSP问题。
苏州历史悠久,是国家首批 24个历史文化名城之一,以其独特的园林景观被誉为“中国园林之城”,素有“人间天堂”、“东方威尼斯”、“东方水城”的美誉。苏州园林是中国私家园的代表,被联合国教科文组织列为世界文化遗产,是人们最好的旅游胜地之一。本文以苏州21个景点为例设定自驾游旅游路线。
1 数据获取及数据预处理
本文选取苏州为旅游目的地,将 21个苏州当地景点设为旅游结点。通过查阅相关数据可得到这21个景点的经纬度、票价和逗留时间等相关信息,如表1所示。
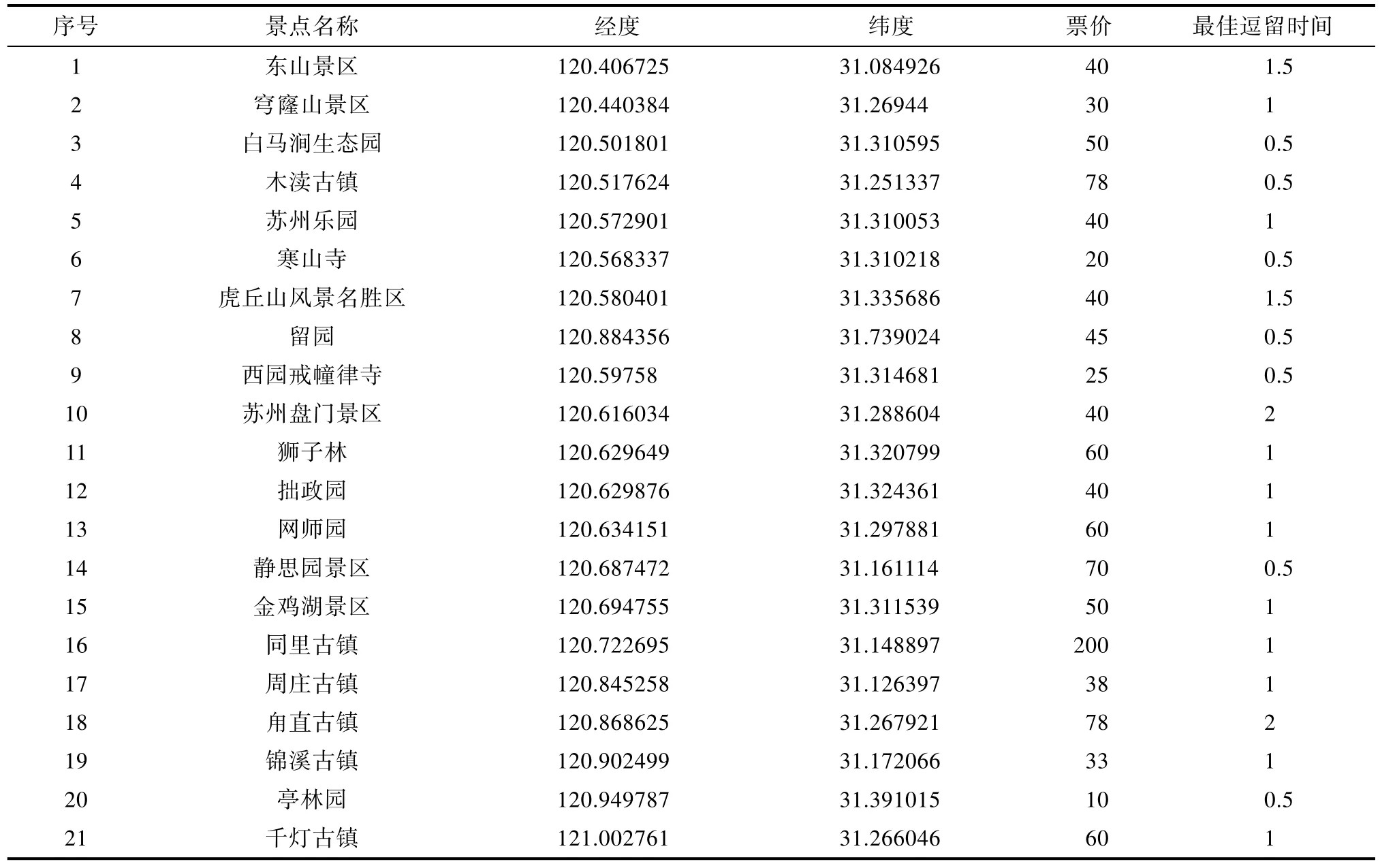
表1 苏州21个当地景点相关信息表Tab.1 Information table of 21 local scenic spots in Suzhou
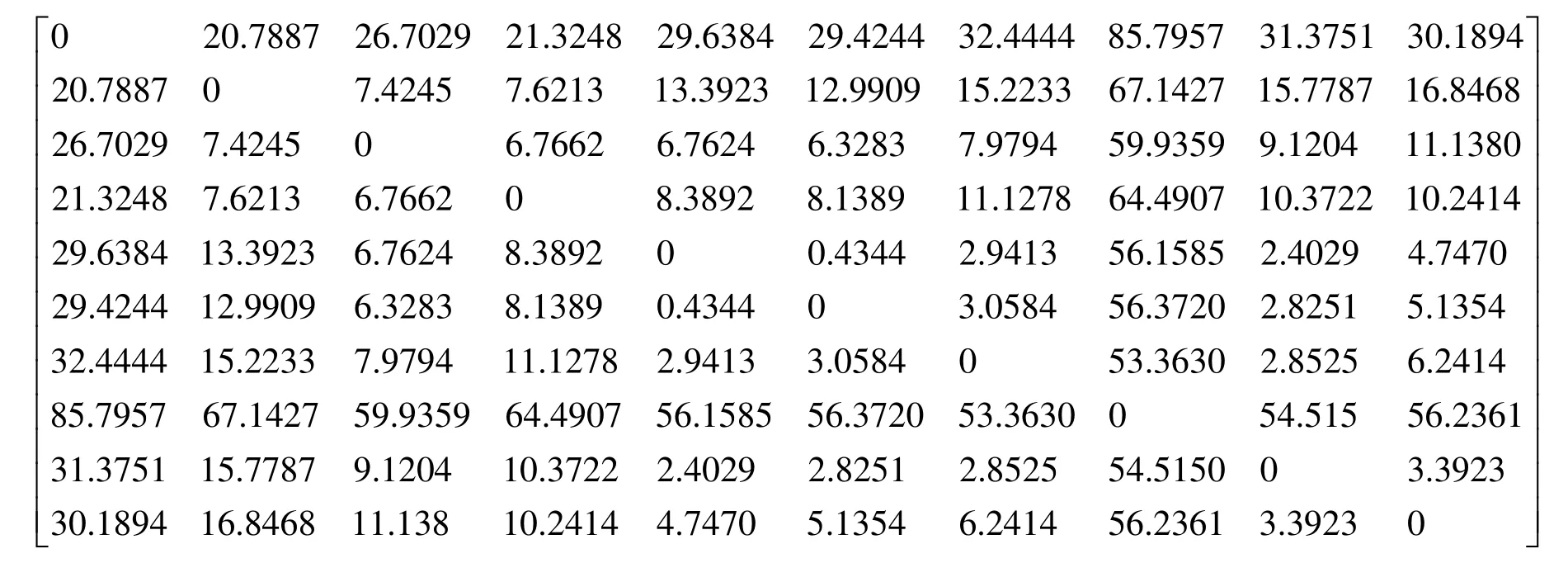
利用MATLAB软件根据经纬度与距离之间的关系,求出21个景点两两之间的最短距离。考虑到苏州作为交通发达的一线城市,苏州内部各景点之间的距离矩阵为对称矩阵。(给出前十个景点之间的最短距离矩阵)
并根据Google earth绘出21个景点的相应的分布图,如图1所示。
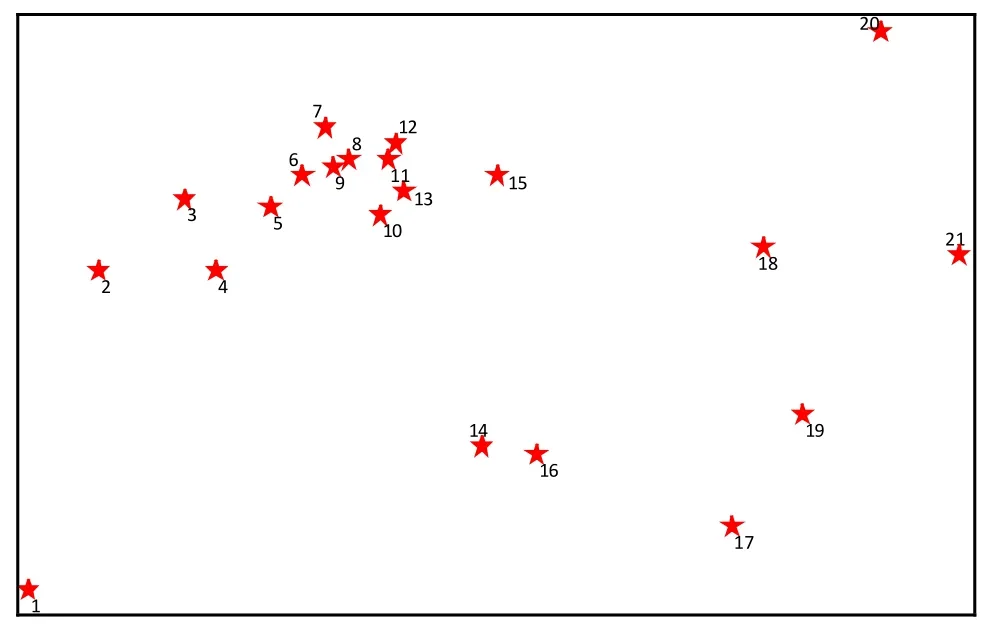
图1 苏州21个景点相对分布图Fig.1 Relative distribution of 21 scenic spots in Suzhou
从图1中可以明显看出,景点2、3、4、5、6、7、8、9、10、11、12、13、15 比较集中,而景点1、14、16、17、18、19、20、21相对分散。这对自驾游路线的规划有一定性的指导作用。
2 基于蚁群算法求解最少遍历路程的模型
2.1 基本蚁群算法
蚁群算法是一种通过模拟自然界蚂蚁寻径的行为的进化算法。蚂蚁在寻找路径时会在路径上释放出一种特殊的信息素,当它们碰到一个还没有走过的路口时,就随机地挑选一条路径前行,与此同时释放出与路线长度有关的信息素,路径越长,释放的激素浓度越低,当后来的蚂蚁再次碰到这个路口的时候,选择激素浓度较高路径概率就会相对较大,这样形成了一个正反馈。最优路径上的激素浓度越来越大,而其它的路径上激素浓度却会随着时间的流逝而消减。蚂蚁通过个体间的信息交流和相互协作找到最优路线。
2.2 聚度和信息权重
在基本蚁群算法中,加速收敛和防止早熟、停滞现象是一对矛盾。为了加速收敛,Ant-Q Sysetm[5]让信息量最大的路径对每次路径的选择和信息量的更新起主要的作用。由于强化了最优信息的反馈,会导致早熟、停滞现象。而MAX-MIN 蚁群系统[6]将各个路径上的信息量的更新限定在固定的范围内,虽然在一定程度上避免了早熟、停滞现象,但在解的分布较分散时收敛速度较慢。本文提出的基于分布均匀度的自适应蚁群算法根据蚂蚁选路的分布均匀情况,动态地调整信息量更新策略和确定每次选择路径的概率,这样,可以在加速收敛和防止早熟、停滞现象之间取得很好的平衡。为此,引入“聚度”的概念来衡量解的均匀程度,从而决定每次选择路径的概率以及信息量更新的策略。当所有路径上蚂蚁的分布相对比较分散时,聚度就较小,此时难以强化最优信息,可能导致搜索速度较慢。因此,要强化正反馈信息,应该让较少的几个较优的路径有较大的概率被选取;在信息量更新时,应该仅让较少的几个较优的路径上的信息量得到较大程度的增强。反之,在所有路径上蚂蚁的分布相对比较集中时,聚度就较大,此时易引起早熟、停滞现象。因此,要使解趋于多样化,应该使较多的路径有可能被选取,在信息量更新时,应该让较多路径上的信息量得以增强。通过这样动态的自适应调节,可以在有效地改善蚂蚁搜索速度的同时避免局部优化。为此,我们在基于分布均匀度的自适应蚁群算法的迭代过程中,根据各条可能的路径上的聚度来确定下一次迭代中可供蚂蚁选择的路径的信息权重,并以此来确定它们被选中的概率。
设从城市i共有r条路径到达另外r个城市i1,i2,…,ir,另设上一次迭代中,经过这r条路径上的蚂蚁数分别为 a1,a2,…,ar,如图2所示。记:
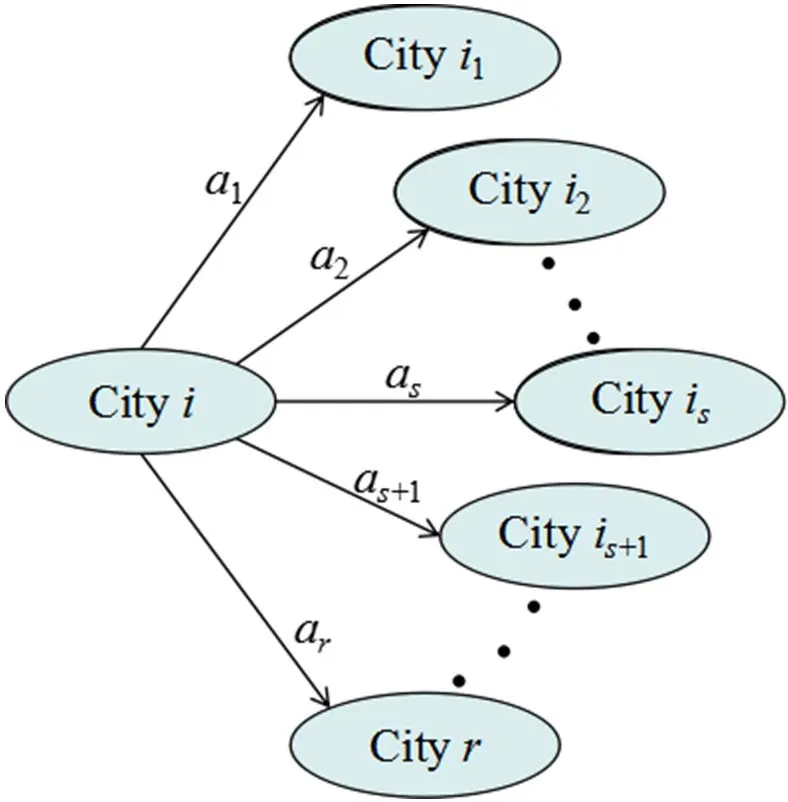
图2 源自城市i的各条路径上蚂蚁的分布情况Fig.2 Ant distribution on each path from city i
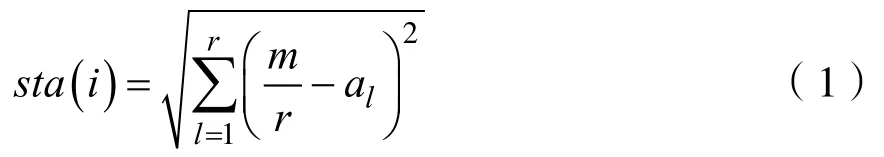
为城市i的聚度[7]。
在改善蚂蚁搜索速度的同时避免局部优化,根据城市i的聚度sta(i)来确定蚂蚁在该城市时下一步可供选择的路径的条数w,这里取:
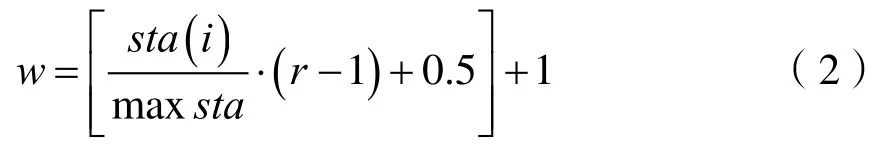
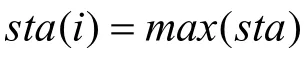
设定信息权重[8]来限制信息量和期望程度对蚂蚁选择路径概率的影响,从而调整各个路径被选中的概率。按照信息量的大小对以城市 i为起点的路径进行排序,将序号存于数组rank中,即数组元素rank[ j]的值为路径(i,j)的序号。由(2)式计算得到的下一步可供选择的路径条数为w,取q=w/ r,记:
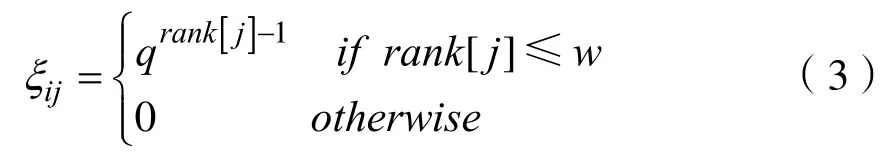
则ijξ为路径(i,j)的信息权重。故蚂蚁在城市i按选择城市j的概率为:
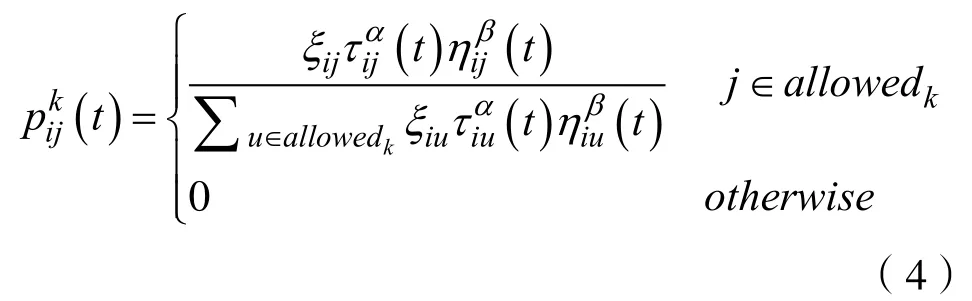
利用信息量的均匀度自适应[9][13]地进行信息量的更新,动态地调整各路径上的信息量的分布,其更新规律为:

Ll(t)为本次迭代中第l只蚂蚁遍历的路径全长。ψl为第l只蚂蚁所对应的解对该路径上的信息量更新的影响程度。ψl的计算方法如下:设经过路径(i,j)的蚂蚁总数为 k,对它们在本次迭代中遍历的路径全长由小到大进行排序,所得序号存放于数组rank1中,即rank1[ l]表示第l只蚂蚁对应的序号,则:
3 基于蚁群算法求解最少遍历路程的模型求解
3.1 蚁群算法操作流程
在本文中,蚁群算法的具体实现步骤为:
Step1:参数初始化
令t=0,设置最大循环次数Ncmax,循环次数 Nc=0 ;
将m只蚂蚁置于n个节点上,在每个节点i放置bi(t)只蚂蚁;
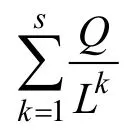
Step2:迭代过程
①对n个城市进行循环
计算城市 i(1≤i≤n)的聚度,并求出选择路径数量w。
②对m只蚂蚁进行循环
当下一步城市j可选择城市数量小于w时,设定阈值0.4r,当w<0.4r时,取q0=0.8;当w≥0.4r时,取q0=0.2
当下一步城市j可选择城市数量不小于w时,可根据:
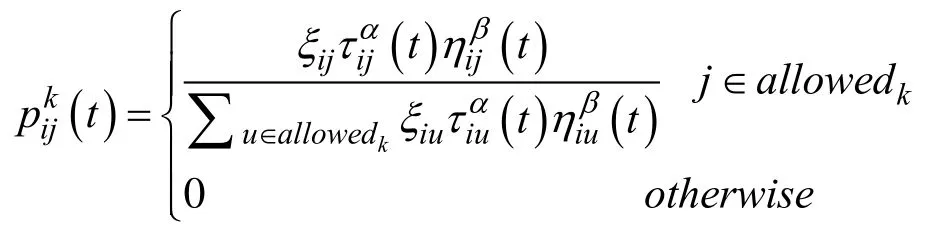
选择城市j;
若选择该路径的蚂蚁数量大于蚂蚁数量的1/3,终止遍历。并根据公式:
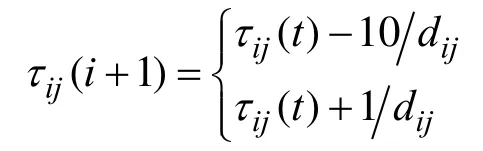
局部更新路径(i,j)上的信息量;
终止蚂蚁迭代的遍历后,按照式(5)对所有城市的各条路径整体更新其信息量。具体算法流程如图3所示。
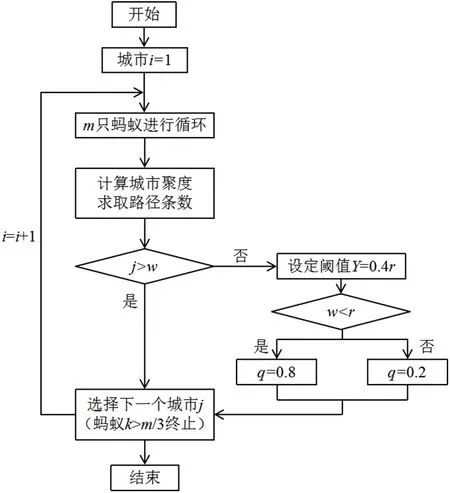
图3 算法流程图Fig.3 Algorithm flow chart
3.2 模型求解结果及分析
利用MATLAB软件进行编程,得到模型求解的结果,如图4所示。
图4 模型求解结果Fig.4 Model solution results
由上图可知最短路线为:
20→18→21→19→17→16→14→10→13→15→11→12→8→9→7→6→5→3→4→2→1
全程路线长度为250.9475km,油价费用约为169.3895625元。
查询相关法律法规[10]可知,苏州市区限速60 km/h,高速公路限速110 km/h,该路线各相邻景点之间所需驾车时间均不大于一个小时,暂不计入时程安排。
游历苏州上述21个景点大概需要21天,门票价格合计为1107元,油价费用约为169.3895625元,食宿另算。实际上,一次性旅行上述21个景点并不实际,这里只是举例介绍,自驾游的人们可根据自己喜好和实际假期时间合理规划自己的行程。
4 结论
本文以苏州为例,建立基于均匀度的自适应蚁群算法的自驾游设计路线模型,以最短路线为标准,相对应的时间和路程费用最小,食宿根据个人喜好以及经济能力自行设定。热衷于自驾游的年轻人可以利用此模型自行设计自己与好友的小长假旅游路线,平时工作忙碌的家庭可在长假时带着妻子与孩子驾车去放松心情,释放压力

