基于局部本构理论的三维筒仓卸载问题研究
关艺璞 周益娴 陈相 张家博

摘要:研究颗粒流的运动规律对核安全学科有重要意义。目前颗粒流的数值模拟方法主要是离散元法。该方法的弊端是计算速度慢。近年来,通过对大量实验和离散元模拟结果进行无量纲分析后,科学家得出了颗粒物质的本构理论,本质上是将颗粒物质看成带有摩擦性质的非牛顿流体。该方法与离散元方法相比能够大大降低运算时间,本文主要研究基于上述本构理论的三维计算在筒仓卸载构型中的适用性。结果表明,出口为矩形情况下,类似二维筒仓(quasi 2D)和二维(2D)筒仓卸载出口流量完全吻合,该三维计算模型得到了验证。且流量满足二维Beverloo关系式。另外,出口为圆形的情况下,流量满足三维Beverloo关系式。证明了该局部本构理论在筒仓卸载三维构型中仍适用。
关键词:颗粒物质 本构理论 流量 筒仓卸载
Study of the Discharge Flow of Granular Media from a Three Dimensional Silo Based on the Local Constitutive Law
GUAN Yipu1 ZHOU Yixian1* CHEN Xiang1 ZHANG Jiabo1
(1. Beijing Key Laboratory of Passive Safety Technology for Nuclear Energy, North China Electric Power University, Beijing, 102206 China)
Abstract: The study of the motion of granular flow is important for nuclear safety. The current simulation method to study granular flow is mainly discrete element simulation. The computational cost of this discrete element method simulation is high. In recent years, by conducting a dimensionless analysis of a large number of experiments and discrete element simulation results, scientists have derived the constitutive law of granular matter, which essentially treats the granular matter as a non-Newtonian fluid with frictional properties. Comparing with the discrete element method, this constitutive law can greatly reduce the calculation time. This work studies the applicability of the three-dimensional simulation based on the constitutive law in the configuration of the discharge of silo. The results show that when the outlet is rectangular, the discharge flow rate of a quasi two-dimensional silo and a real two-dimensional silo are completely consistent. Thus, the three-dimensional simulation model has been verified. And the two-dimensional Beverloo law has been recovered. In addition, when the outlet is circular, the three-dimensional Beverloo law has also been recovered. This demonstrates the applicability of the local constitutive law in the three-dimensional configuration of silo discharge.
Key Words: Granular media; Constitutive law; Flow rate; Discharge of silo
0 引言
反應性事故发生后,核燃料棒可能会在侧面产生破口,并且核燃料物发生破损后形成颗粒状碎片,它们将从容器内泄漏出来与冷却水发生剧烈反应。这些颗粒物质的动量将对其与冷却剂碰撞后果产生影响,因此研究颗粒流的运动规律对核安全有重要意义。颗粒物在筒仓中的流动是与核事故发生后颗粒物质流动最为接近的场景。实验证明,当筒仓高度和宽度足够大时,与普通流体不同,颗粒物卸载的流量总是保持恒定。沙漏流这一特性至今还没有准确的物理解释。目前颗粒流的数值模拟方法主要是离散元法。该方法的弊端是计算速度慢。近年来,通过对大量实验和离散元模拟结果进行无量纲分析后,科学家得出了颗粒物质的局部本构理论,本质上是将颗粒物质看成带有摩擦性质的非牛顿流体。该连续数值模拟方法能够大大降低运算时间。目前文献中主要是利用连续数值模拟计算来求解二维颗粒流构型,本文将研究基于上述局部本构理论的连续数值模拟方法在筒仓卸载三维构型中的适用性。
1 筒倉卸载流量规律
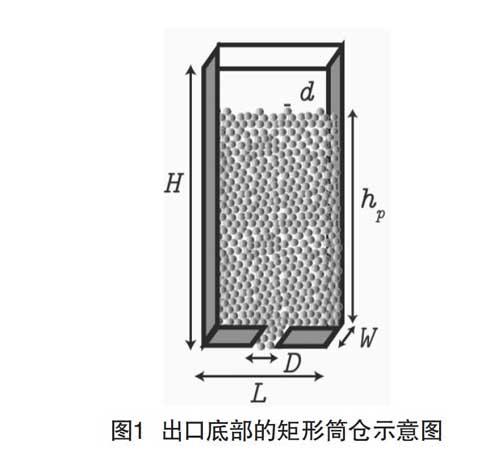
为研究基于局部本构理论[1,2]的三维计算在本问题中的适用性,我们将着重研究颗粒物流量规律。最被广泛使用的颗粒物完整流量公式为Beverloo等[3,4]提出的经验公式,对于一个充满颗粒物的平底筒仓(如图1所示),充满质量密度为,体积分数为,直径为的颗粒物,质量流量可记作:
其中和均为常数,代表维数。该公式长期以来被广泛使用且能准确预测颗粒流量规律。
2连续数值模拟
我们采用连续数值模拟软件Basilisk,Basilisk为开源纳维-斯托克斯公式求解器[5],求解方程为:
此处表示应变速率张量)/2,为有效黏性系数,对于颗粒物质,它的表达式为:
其中为摩擦系数,为局部压强,为应变速率张量的第二不变量,,
I为惯性系数,表示颗粒物的微观排列时间与宏观变形时间之比:
摩擦系数与无量纲惯性系数的关系为:
,以及均为常数。根据文献[6,7],我们选取,,。
3 结果与分析
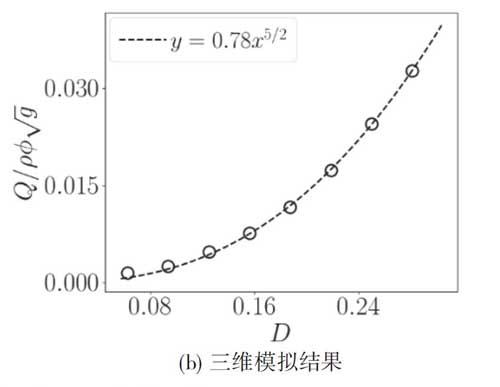
首先,为验证三维计算的正确性,我们对出口也为矩形的三维矩形筒仓进行模拟(如图1所示),将前后壁面设置为滑移边界条件,则等效于二维筒仓问题。其中筒仓宽度,颗粒物高度取为。我们在图2(a)中展示了类似二维筒仓(quasi 2D)和二维(2D)筒仓卸载出口无量纲流量与出口尺寸的关系,可以看出二者结果完全吻合,验证了三维计算的正确性,且流量关系式满足方程(1),即无量纲流量与出口直径成正比。在该计算中,我们并未考虑颗粒物体积分数对于流动状态的影响,因此可忽略颗粒物尺寸的影响,我们设置Beverloo关系式中的为0,得到常数,与文献中实验所得常数相近[8]。接下来,为进一步验证三维流量关系式,我们模拟出口为圆形的三维情况,筒仓宽度,颗粒物高度取为。图2(b)中展示了三维筒仓卸载出口无量纲流量与出口尺寸的关系,由图中可以看出,流量关系式仍旧满足方程(1),即无量纲流量与出口直径成正比。可见局部本构理论计算在筒仓卸载三维构型中仍旧适用。
4 总结
本文采用基于局部本构理论的三维连续数值模拟,研究筒仓卸载流量与出口尺寸之间的关系。模拟结果表明,出口为矩形情况下,类似二维筒仓(quasi 2D)和二维(2D)筒仓卸载出口流量完全吻合,该三维计算模型得到了验证。且流量满足二维Beverloo关系式。另外,出口为圆形的情况下,流量仍旧满足三维Beverloo关系式。证明了该局部本构理论在筒仓卸载三维构型中仍旧适用。
参考文献
[1] A. Bhateja and D. V. Khakhar. Rheology of dense granular flows in two dimensions: Comparison of fully two-dimensional flows to unidirectional shear flow[J]. Physical Review Fluids, 2018, 3:062301.
[2] W. Jin, J. J. Stickel, Y. Xia et al. A Review of Computational Models
for the Flow of Milled Biomass
Part II: Continuum-Mechanics Models[J]. ACS Sustainable Chemistry & Engineering, 2020, 8:6157-6172.
[3] W. A. Beverloo, H. A. Leniger, and J. V. de Velde. The flow of granular solids through orifices[J]. Chemical Engineering Science, 1961, 15:260–269.
[4] F. Alonso-Marroquin and P. Mora. Beverloo law for hopper flow derived from self-similar profiles[J]. Granular Matter, 2021, 23(7) :1-8.
[5] S. Popinet. A vertically-Lagrangian, non-hydrostatic, multilayer model for multiscale free-surface flows[J]. Journal of Computational Physics, 2020, 418:109609.
[6] Y. Zhou, P.-Y. Lagrée, S. Popinet et al. Gas-assisted discharge flow of granular media from silos[J]. Physical Review Fluids. 2019, 4:124305.
[7] Y. Zhou, P.-Y. Lagrée, S. Popinet et al. Experiments on, and discrete and continuum simulations of, the discharge of granular media from silos with a lateral orifice[J]. Journal of Fluid Mechanics, 2017, 829:459-485.
[8] M. Benyamine, M. Djermane, B. Dalloz-Dubrujeaud, et al. Discharge flow of a bidisperse granular media from a silo[J]. Physical Review E, 2014, 90(3): 032201.

