具有避障的机器人集群系统分布式编队控制

刘 伟，李大卫，戴洪德，李 飞

(海军航空大学,山东 烟台 264000)

0 引言

多机器人系统(又称机器人集群系统)的协同控制问题受到广泛的关注。这主要是因为单体机器人的载荷及其能力有限，无法完成更为复杂的任务[1-4]。不同机器人可以携带不同的任务载荷，通过相互协调配合，共同完成复杂的任务，其可广泛应用在军事、交通或者服务等多个领域[2]。其中，机器人集群的编队控制问题是该系统协同控制中的一个关键技术点。有关编队控制的研究成果，主要的编队控制方法可以分为如下几类：跟随领航者法、虚拟结构法、基于行为控制法和人工势场法[5]。通常为了解决某些实际问题，也会将如上几类方法组合使用。

随着研究的深入，研究重点也从编队控制转移到考虑实际应用限制因素和改善控制品质等方面。尤其是在机器人集群系统中，机器人数量急剧增多的情况下，由于通信距离受限制，或者移动过程中受到障碍物遮挡，单个机器人难以获取所有机器人的信息，因此，传统的集中式编队控制方式，已经难以适应集群系统的应用需求[5]。取而代之的是设计分布式的编队控制器，通过局部的信息交互，实现整个集群系统的编队行为。

近年来，多智能体协同控制理论蓬勃发展。其中一致性控制问题受到广泛关注[6-8]。所谓一致性控制，即是智能体系统，通过通信网络交互，基于分布式的设计框架，设计非集中式的控制协议，进一步从宏观上表现为一个群体的行为同步[9-13]。多智能体系统的一致性协同控制内涵，由于其与机器人集群系统的任务需求相契合，其理论在近几年被应用到无人系统的编队控制中[14-16]。需要指出的是，这些文献中，关于无人系统之间的通信拓扑是假设为无向的。而在实际应用中，机器人的通信可能会因为故障而只能接收，或者因为不同的个体发射功率不一样，导致通信结构是单向的，从而使得拓扑结构为非对称的有向图，该类型的拓扑结构可将无向拓扑视为其一个特殊情况。

另外，机器人在编队行进中，安全是需要考虑的重要因素。如何使单个机器人系统有效躲避障碍物，得到了大量的研究结果。其中，人工势场方法广泛应用于航迹规划[17]以及无人机避障[18-20]。

因此，针对机器人个体数量众多的机器人集群系统，在有向通信拓扑结构的条件下，设计分布式控制器的同时考虑机器人编队的避障问题，更具有实际意义。为了解决这一问题，本文针对机器人系统集群系统，将机器人之间的通信拓扑建模为非对称的有向拓扑图，设计分布式机器人的编队控制器，并利用多智能体系统一致性理论研究系统编队形成的条件。

1 问题描述

1.1 系统模型

本文假设机器人集群系统包含N个机器人，单个机器人具有如下的系统运动学模型

(1)

pi∈R2，vi∈R2，ui∈R2分别是第i个机器人的二维状态(位置和速度)和控制输入。进一步可将系统写成如下的形式

(2)

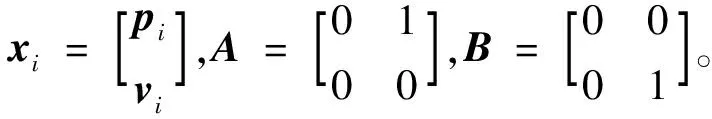
1.2 编队队形定义

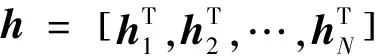
定义1.如果由多机器人组成的机器人集群系统满足如下的条件：

则称系统实现了期望的编队队形h。其中，Δij=hi-hj表示两两机器人相互之间的相对速度和位置。

1.3 通信拓扑描述

在机器人集群系统中，由于机器人的数量较多，单个机器人无法获取全部机器人信息。因此，本文采用图论中的有向图来描述系统内机器人之间的信息交互关系，如图1所示。

图1 机器人之间的有向通信拓扑图

2 基于一致性的分布式编队控制

2.1 控制器设计

设计的分布式编队控制器为

(3)

aij为A的元素;K∈R2×2是反馈矩阵;c>0表示状态参数相互之间的耦合强度;hi为机器人i的编队队形描述，如1.2节所述。

根据邻接矩阵A的定义可知，每个机器人无法知晓所有机器人的状态信息，仅能够同自己的邻居之间进行信息交流。邻居的定义可以是一定通信距离范围内机器人，也可以定义为同一个通信群组里面的机器人。aij≠0，表示机器人i和机器人j为邻居关系，反之则aij=0。由此可以看出，本文构建的控制器是分布式的。

根据前面设计的控制器，可以到的整个集群系统的闭环运动学方程为

(4)

2.2 问题转换

根据机器人编队的定义1，引入如下的变量替换ei(t)=xi(t)-hi，i=1,2,…,N。根据ei(t)的定义可以得出结论：如果ei(t)→ej(t),∀i,j∈N，也就是如果变量ei(t)(i=1,2,…,N)能够达成一致，则定义1中的条件满足，即编队达成期望的编队队形[21]。

进一步，构建如下的编队偏差变量ξi(t)=ei(t)-ei+1(t),i=1,2,…,N-1，由其定义可知，如果变量ξi(t)→0，t→∞，则ei(t)→ej(t)，∀i,j∈N，且有

2.3 主要结论

根据2.2节的描述，令E=[-1N-1,IN-1]∈R(N-1)×N，F=[0N-1,IN-1]，可以将式(4)写成如下形式

(5)

R=ELF。由文献[21-23]可知，当机器人之间的通信拓扑图包含一个有向生成树时，矩阵R的特征值的实部均大于0。

定理1.机器人集群系统能够实现编队队形h，如果存在一个c和一个正定对称矩阵P2使得如下不等式成立：

ATP2+P2A-cαP2BBTP2<0

(6)

其中，P1满足如下条件的正定矩阵

P1R+RTP1>αP1

(7)

R=ELF，0<α<2min{Re(λ(R))}，Re(λ(R))为矩阵R特征值的实部，且反馈矩阵可以设计为K=BTP2。

证明：构建如下的李雅普诺夫函数

V=ξT(P1⊗P2)ξ

(8)

P2满足不等式(6)，P1为一个满足如下的条件的正定矩阵

P1(R)+(R)TP1>αP1

(9)

0<α<2min{Re(λ(R))}，R=ELF。

令K=BTP2,则有

ξT(P1⊗P2)(IN-1⊗A-cR⊗BK)ξ=

ξT[P1⊗(ATP2+P2A)-c(RTP1+

P1R)⊗P2BBTP2]ξ

(10)

因为P1R+RTP1>αP1，则

(11)

由式(6)可知

ATP2+P2A-cαP2BBTP2<0

(12)

进而

(13)

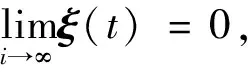
3 考虑避障的机器人编队控制

在前一节的控制律设计中，仅考虑了机器人编队形成条件。考虑到实际应用条件，需要进一步考虑机器人运动时避障问题。因此，需要在控制器(3)基础上引入避障的控制。本文利用人工势场函数方法，设计机器人避障控制项。

机器人i和障碍物o之间的距离lio为

(14)

Pi和(xi,yj)分别为机器人i的位置和坐标，Po和(xo,yo)分别为障碍物所在位置和坐标。

给出如下的人工势场函数

(15)

参数k为机器人之间的斥力系数；Uio为障碍物对机器人产生的排斥力场;lo,max为机器人距离障碍物的安全距离。

由人工势场函数的定义可以看出，当机器人之间距离lij大于安全距离lmax时，机器人之间不会因为势场函数发生作用，而当lij小于安全距离lmax时，势场函数发生排斥作用。

由此可得作用在机器人i上的合力为合势场的负梯度,为

(16)

机器人i的避障控制器uico为

uico=Fi

由此可得具有避障功能的机器人i的控制器为

(xi(t)-hi)]+uico

(17)

4 数值仿真

4.1 参数设置

假设有4个机器人组成集群系统，机器人的在二维平面运动，令机器人集群系统期望的队形是一个边长为100的正方形，速度为0.01，故期望的编队可表示为：hi(t)=[0,0.01,0,0.01]T，h2(t)=[100,0.01,0,0.01]T，h3(t)=[100,0.01,100,0.01]T，h4(t)=[0,0.01,100,0.01]T。机器人之间的通信拓扑结构如图2所示。

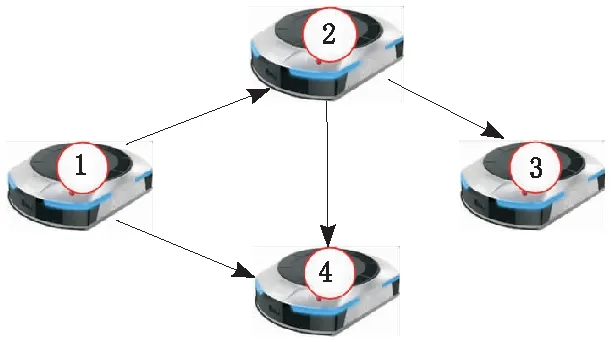
图2 机器集群的通信拓扑图

由图2可以看出，各机器人无法获取全部4个机器人的信息。例如，3号机器人仅能够获取2号机器人的信息。该通信拓扑图对应的拉普拉斯矩阵L为

4.2 仿真结果

设置机器人避障的安全距离为100，障碍物的位置在(400，300)，得到仿真结果分别如图3～图6所示。

图3和图4分别为所有机器人在x和y方向上的位置和速度随时间变化情况。由图3和图4可以看出，当机器人运动到障碍物之前，约在仿真时间为25 s时，机器人之间的速度趋于相同，编队相对距离保持不变，即形成了编队。而当遇到障碍物时，约在仿真时间35 s 时，其速度和编队相对距离发生变化，从而躲避障碍物，此时编队队形被破坏，如图3和图4所示。当越过障碍物后，约在仿真时间80 s时，机器人编队再次形成。在前文分析中，定义的编队误差向量ξ(t)随时间变化趋势如图5所示。在x和y方向上，误差向量逐渐趋于0，由此可以看出机器人完成了编队。而当遇到障碍物时，约在仿真时间35 s附近，编队误差不再为0。出现这种情况的原因是，编队在躲避障碍物，此时编队队形被破坏。当越过障碍物后，约在仿真时间80 s时,机器人编队再次形成。

图3 机器人的位置曲线

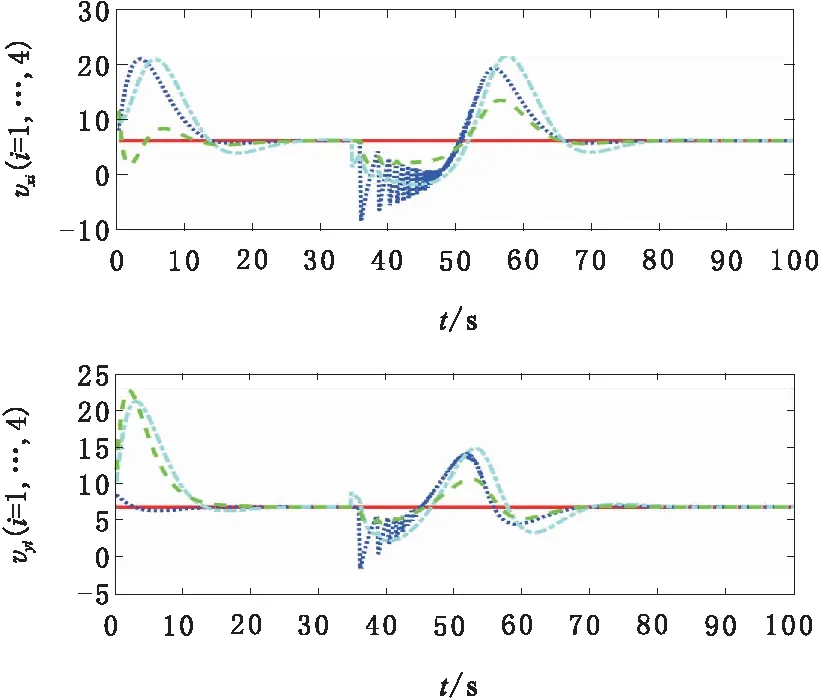
图4 机器人速度曲线

图5 编队误差变量ξ(t)变化曲线

在图6中画出了机器人集群系统完成编队并在遇到障碍物进行避障的过程。圆形的圆心位置为障碍物的位置(400，300)，根据仿真设置要求，编队对障碍物的安全距离为100。在仿真开始不久，完成了期望的编队队形。而当遇见障碍物时，机器人的编队队形被破坏，各机器人躲避障碍物，如图6所示。这是由于避障的优先级要高，因此在越过障碍物后，机器人编队队形再次形成。由图6中的机器人运动轨迹可以看出，机器人运动轨迹没有同障碍物的安全线交联，这表明机器人编队可以有效躲避障碍物。

图6 机器人集群系统编队形成及避障

5 结束语

本文利用多智能体一致性理论研究了机器人集群系统的编队控制问题，构建了分布式的编队控制律，得到了机器人实现编队的充分性条件。同时，利用人工势场函数方法设计避障控制器，最后用数值模型进行了仿真验证。在进行避障的过程中，机器人队形遭到破坏。下一步，将继续研究如何控制机器人在行进避障过程中使得编队队形保持不变。