基于全和谐型浅水方程的有限体积海啸数值模型开发与应用

周文，王培涛，王岗*，于福江，郑金海，梁秋华

( 1. 海岸灾害及防护教育部重点实验室（河海大学），江苏 南京 210098；2. 国家海洋环境预报中心，北京 100081；3. 拉夫堡大学 建筑与土木工程学院，英国 莱斯特郡 LE11 3TU)

1 引言

海啸作为最具危险性和破坏力的海洋灾害之一，给沿海地区造成了巨大的经济损失和人员伤亡。如1960 年5 月22 日智利瓦尔迪维亚（Valdivia）发生9.5 级大地震，这也是人类历史上用仪器监测到的最强地震，随之引发的巨大海啸，在当地的海啸波波高达25 m，对附近一个居住着250 万人口的城镇造成约1 万人死亡、500 亿～700 亿美元的经济损失。此外，该海啸还影响了整个太平洋海域，导致了太平洋另一端的日本数百人丧生[1]。

为了应对海啸灾害，人们在海啸监测、预报和致灾机理等方面做了大量研究。由于人类史上灾难性的海啸主要是由地震引起的，因此人们通过铺设海底地震仪、投放海啸浮标和设置沿岸验潮站等建立海啸监测网。地震仪和观测海底变形的大地传感器等通过海底线缆将数据传输给陆上监测中心。海啸浮标系统主要是美国国家海洋与大气管理局（NOAA）下属太平洋海洋环境实验室研制的海啸深海评估和报告浮标系统（Deep-ocean Assessment and Reporting of Tsunamis, DART），它是由海底压力记录仪、海表浮标和地球同步气象卫星构成的立体监测系统[2]，目前已更新至第4 代。目前全球海域设置了60 多个DART和900 余个验潮站[3]，覆盖全面的大洋与近岸监测网为海啸预警以及海啸研究提供了大量可靠的原始数据。

随着计算机和数值计算技术的发展，数值模拟已成为海啸的主要研究方法并在海啸预警系统中起到了关键作用。目前常见的海啸模型可主要分为基于浅水方程的静压模型和考虑波浪动水压力的数值模型两类。第1 类是基于浅水方程的数值模型，由于其计算效率高且在大多数模拟过程均能得到较好的结果，应用最为广泛。华盛顿大学LeVeque 教授团队在1994 年发布了用于求解双曲型方程的软件包Clawpack（Conservation Laws Package），且其版本一直在不断完善与更新[4]。2010 年GeoClaw[5]作为Clawpack求解浅水方程的模块用于海啸模拟。GeoClaw 包含笛卡尔坐标和球坐标两种形式，基于高分辨率激波捕捉的有限体积法进行数值求解，同时采用自适应网格嵌套技术并考虑了干湿边界的模拟。第2 类常见的海啸模型主要是基于Boussinesq 方程，考虑了波浪的频散性。美国特拉华大学建立了基于完全非线性Boussinesq 型方程的波浪模型—FUNWAVE[6]。该模型此后进一步更新为TVD[7]及GPU[8]版本。Yamazaki等[9]建立了直接求解Navier-Stokes 方程的非静压波浪模型模拟海啸的传播演化过程。Zhao 等[10]基于Green-Naghdi 理论建立了考虑海底动态可变的非静压波浪模型模拟二维和三维的海啸传播过程。

虽然第2 类海啸模型有更高的数值精度，但考虑到海啸预报的时效性，目前海啸模型中仍以浅水方程数值模型居多。早期的部分海啸模型如MOST[11]等采用有限差分法（FDM）求解控制方程，其优点是简单成熟，方便构造高精度的计算格式，然而处理复杂网格时不够灵活[12]。由于有限体积法（FVM）数学表达直观、物理涵义清晰、满足守恒规律且能方便地捕捉浅水方程中的间断解[12]，已逐渐成为一种重要的数值模型方法。浅水方程的有限体积数值求解主要涉及源项与通量的处理以及动边界（干湿边界）的准确模拟。关于源项与通量的处理目前主要是通过不同的数值方法用以平衡有限体积法中的通量梯度和源项[13-15]。而动边界的准确模拟目前主要基于Riemann近似解。HLL（Harten, Lax and van Leer）Riemann 近似求解器[16]在1983 年提出，它根据有限体积单元界面处左右波速的预测值将界面通量值的计算划分为3 个区域，能够很好地解决一维浅水流动问题。在此基础上，HLLC Riemann 近似求解器[17]考虑了二维问题中另一个方向的横波影响，将单元界面通量值的计算划分为4 个区域，用以简便和精确地求解二维浅水波动问题。为了合理简洁地模拟动边界，Liang 和Borthwick[18]提出了全和谐型浅水方程，以自动满足控制方程通量与源项的守恒，并通过对地形重构抑制单元内的虚拟流动，开发了一种高性能强稳定性的浅水数值模型。该模型数值方法操作简便且自动满足单元体积各参量守恒，已被包括FUNWAVE 等数值模型广泛采用[7]。

由于灾害性海啸的影响通常波及整个大洋甚至全球范围，本文基于球坐标系下的全和谐型浅水方程建立了有限体积海啸数值模型。考虑到海啸不仅会对桥墩、防波堤等近海建筑物产生影响，也会造成近岸大面积的陆地淹水，因此海啸近岸爬高的精确模拟也是海啸数值模拟的重要技术要求。沿海地区往往是经济较为发达的区域，不仅存在着复杂的自然地形还涉及大量的人工建筑物。本文采用地形重构的方法，以模拟海啸在此复杂地形上的近岸爬高过程。本文所建立的海啸数值模型应用于2015 年9 月16 日智利Mw8.3 级地震海啸的模拟，以验证模型对越洋海啸模拟预报的能力。

2 控制方程

越洋海啸的传播需要考虑地球的曲率和地转偏向力的影响，因此控制方程选取考虑科氏力的球坐标系下的非线性浅水方程，其矩阵形式为[19]

式中，θ和φ分别为地球的经度和纬度；t为时间；向量U为变量；F和G分别是θ和φ方向的通量；S为源项；具体为

式中，r为地球半径；ξ为相对于静止海平面的波面位移；hs为静水深；h=ξ+hs为总水深；uθ和uφ分别为θ和φ方向沿水深平均的速度。源项中第2、第3 项分别对应科氏力和摩阻项，其中f=2ωsinφ为科氏力系数；ω为地球绕地轴自转的角速度；Cf=gn2/h1/3为底摩阻系数，n是Manning 系数。

为了平衡通量和源项，本文利用Liang 和Borthwick[18]提出的全和谐型浅水方程表达形式改写源项式（5）中波面的空间导数。以θ方向为例，有

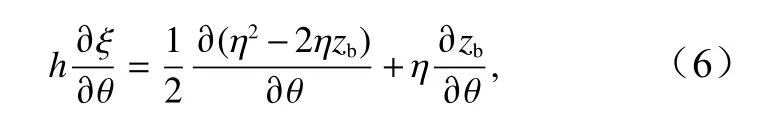
式中，zb为基准线上的海底地形高程；η=zb+h为波面高程。

在此不考虑zb和hs随时间t改变，从而有

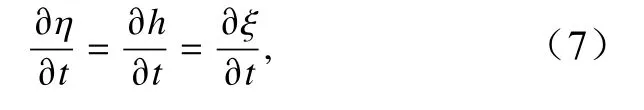
因此式（2）至式（5）的最终形式为

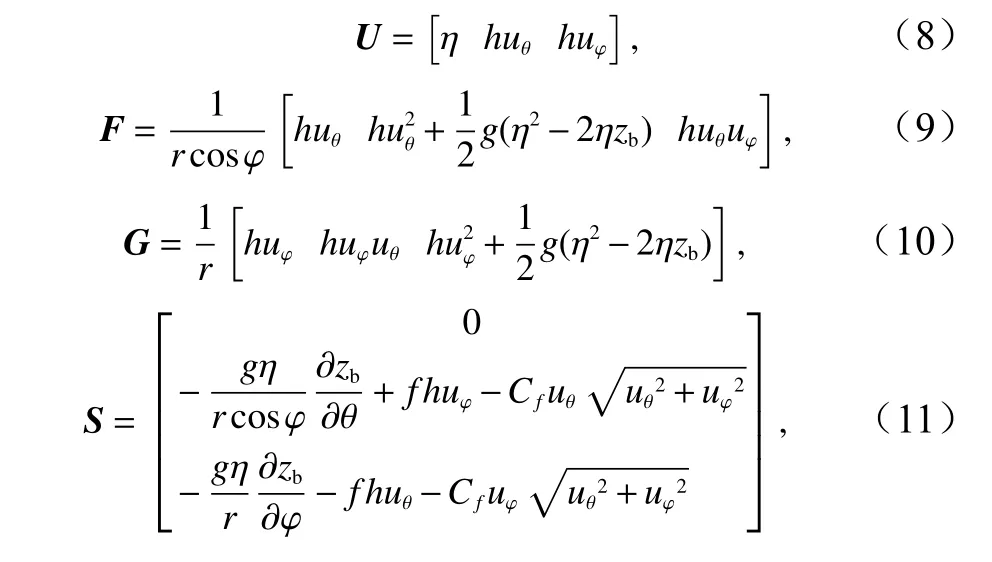
式（9）至式（10）将地形梯度分离至方程右侧的源项中用以平衡方程左侧通量的变化，从数学表达上保证了方程的守恒形式。

此外，为方便模型用于小范围特别是物理实验的模拟，本文在建立球坐标模型的同时也开发了笛卡尔坐标海啸模型。由于两套方程的数值求解方法完全一致，后文将统一介绍。

3 数值方法

本文基于均匀矩形空间单元，利用Godunov 格式的有限体积法[18]求解方程矩阵。基于MUSCL-Hancock 格式，采用HLLC Riemann 近似求解器[17]计算单元界面上的流体通量，保证数值格式在时间和空间上均为二阶精度。

3.1 MUSCL-Hancock 格式

3.1.1 预测步

首先在时间上求解半个时间步（Δt/2）对应的流体变量预测结果

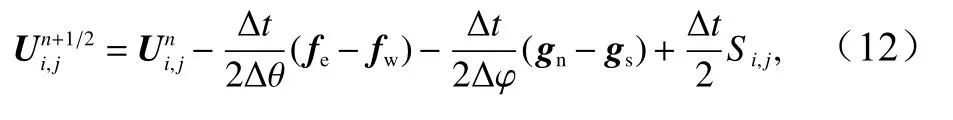
式中，上标n代表第n时刻；i、j为有限体积单元标号；Δθ、Δφ表示球坐标系水平方向的单元大小；fe、fw，gn、gs分别代表单元东、西、北、南4 个方向的流体界面通量。单元界面的流体变量利用MUSCL 线性重构计算[20]，以单元东西界面为例

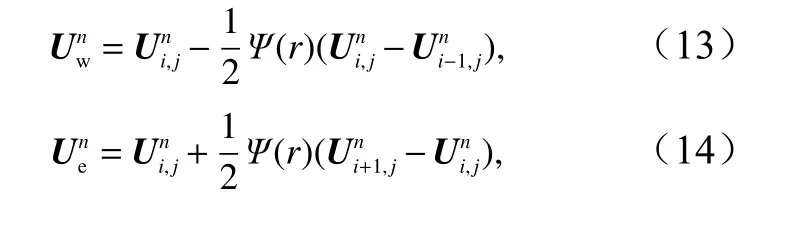
此外，源项中海底地形底坡项直接利用中心差分法离散，科氏力项直接代入计算即可，而摩阻项后文详细介绍。

3.1.2 校正步

在校正步将变量递进至完整的时间Δt，具体为

式中，FE、FW、GN、GS分别为求解Riemann 问题得到的单元四周的流体界面通量，单元界面处Riemann 变量的求解依然利用MUSCL 线性重构[20]。

3.2 干湿边界

为了准确模拟波浪在陆地和海洋边界处的运动，本文采用Liang[21]提出的地形重构方法。以单元东界面为例，为了确保计算过程中单元的水深恒为正，则地形重构为

式中，上标L 和R 分别表示界面的左右侧。对应的水深为

综合式(17)至式(19)可求得Riemann 变量η和q。

为了使干湿边界的处理不失一般性，考虑如图1干湿单元相邻的情形。单元(i,j)的东界面通量的计算仍以地形为基线，而西界面的计算基线为水面线，假设水面静止，东侧地形高于西侧则水面不会发生流动，而数值计算时单元(i,j)内会引入从东至西的通量。为了避免虚假通量的引入，进一步修正zb与η为

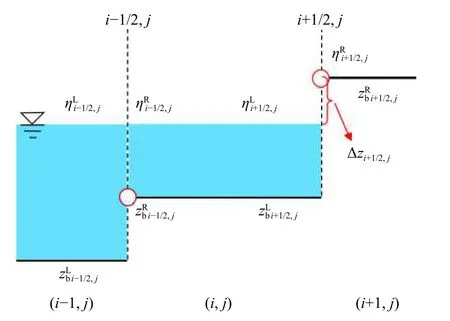
图1 地形重构示意Fig. 1 Local topography reconstruction

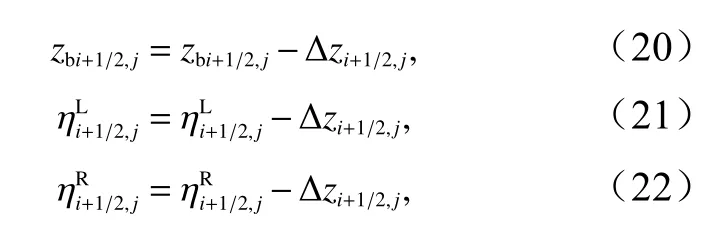
其中

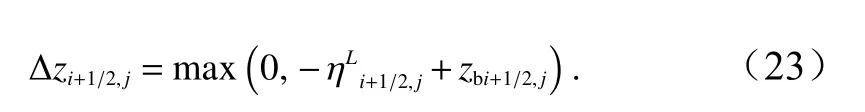
经过上述修正，东西界面的计算基线得到统一，保证了通量计算的平衡性。

3.3 底摩阻

在利用MUSCL-Hancock 格式数值求解后进一步利用分裂格式(splitting point-implicit scheme)对摩阻项离散[22]，其等价于求解以下常微分方程

式中，Sf为摩阻项，单宽流量q=[huθ huφ]T，其随时间演进的计算为

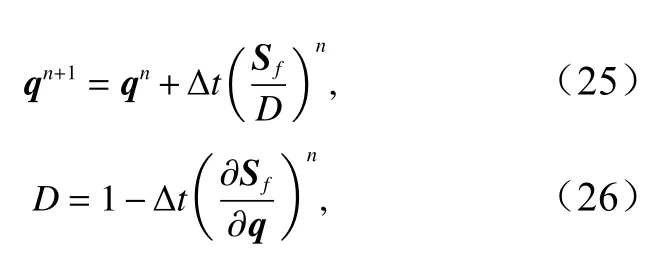
式中，D为隐式系数，设F=(Sf/D)n。为了确保干湿边界附近数值计算的稳定性，对F设置阈值

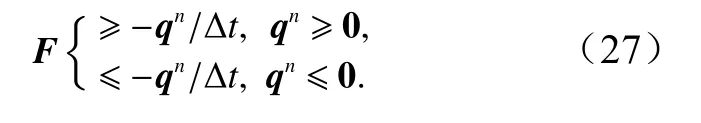
其物理意义是摩阻作用至多会使流体停止运动而不产生逆向流动。

3.4 边界条件和稳定性准则

如图2 以某个方向第一个单元为例，边界处虚拟单元的变量利用相邻单元的值近似处理，单宽流量q的取值根据边界类型而变化。对于开放边界，有

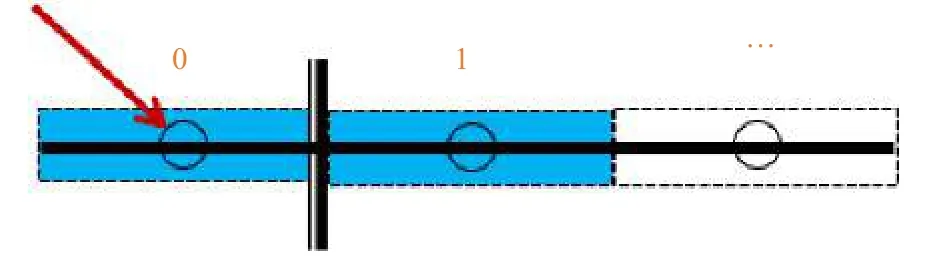
图2 边界条件示意图Fig. 2 Sketch of boundary condition

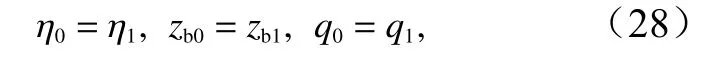
对于闭合边界、即全反射边界，有

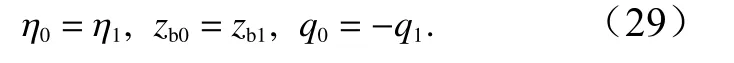
为了保证数值计算的稳定，时间步Δt的确定遵循Courant-Friedrichs-Lewy (CFL)准则

虚拟网格

式中，C为Courant 系数；ΔSθ和ΔSφ分别为经度与纬度方向的单元空间长度。

3.5 海啸源模型

由于历史上灾害性海啸几乎都是由地震所引起的，所以海啸源模型主要考虑地震引起的海水波动过程，它是海啸数值计算的基础，其适用性直接影响海啸波的传播及海啸与海岸间相互作用。自Steketee[23-24]把位错理论引入地震学后，许多地震学者针对不同的断层类型发展了不同的位错理论，使得计算地球同震形变的方法得到不断发展。Kajiura[25]首次提出可以将静态的海底位移转化成海啸产生阶段自由表面的初始边界条件，使得地震海啸数值模拟过程进一步简化。为此，利用断层模型计算地震引发的海床位移量，从而估算出海底形变引起初始水面高度来初始化海啸数值模型已成为海啸模拟的惯用方法。目前，Mansinha 和Smylie[26]以及Okada[27]基于弹性错移理论发展的两套断层模型被广泛应用，大量的研究和应用实例表明此类模型对逆冲断层地震海啸源计算具有较好的适用性[28-30]。Okada 模型[27]计算海底同震位移需要输入7 个震源参数，分别为震中位置、震源深度、断层走向角、倾角、滑动角、滑移量以及断层破裂的尺度（断层长度及宽度）。震源基本信息（震中位置、震源深度）可由地震速报系统测定，而震源机制角可由W-phase 反演系统得到。震源的尺度和滑移量可参考震级与破裂尺度经验关系率估计[31]。需要说明的是，上述方法在海底较为平缓且为典型的逆冲断层条件下较为适用。当地震引起陡坡大范围的水平运动或者地震引起断层水平运动比垂向运动大得多的走滑断层时应该考虑水平位移在海啸产生过程中的贡献。

4 2015 年智利地震海啸数值模拟

2015 年9 月16 日22:54:32（UTC）位于纳斯卡板块和南美洲板块之间的南美洲俯冲带发生Mw8.3 级地震。震中位于31.57°S, 71.67°W，距离智利伊亚佩尔市以西48 km，震源深度为22.4 km。该地震引发了太平洋范围的中等强度海啸，造成近场地区30 多人伤亡，经济损失高达6 亿美元[32]。

4.1 海啸产生阶段模拟

考虑海啸预警业务化需求，通常假定海底地震具有一致震源机制特征，采用点源、单断层面和平均滑动量的假定以简化断层破裂的复杂性，忽略了断层破裂的局地特征以便最短时间内给出相对合理的震源破裂特征。自Kanamori 和Rivera[33]提出基于W 震相测定地震矩张量的方法后，全球多个预警中心基于W 震相研制出了中强震矩心矩张量反演系统。基本实现在震后8～15 min 准确获取全球Mw≥6.5 地震的震源机制解，从而有效提高了海啸定量预警及时性。表1 为2015 年智利Mw8.3 级地震断层基本参数，其中地震断层破裂尺度和滑移量依据Wu 等[31]关系率估算所得，即地震断层长度约为212 km，宽度约为79 km，平均滑移量6.3 m。断层尺度量级与记录的深海海啸波长对比相当，估算的结果可信。选择USGS 快速W-phase 解作为该事件的震源机制解，从震源机制解可知该地震断层为典型的低倾角逆冲断层，因此可利用Okada 弹性位错理论模型[27]计算海啸传播模型所需的海表面初始形变（图3）。从海表面初始形变分布可知主要的形变呈轻微NNE 向的扁状椭圆形分布，纬度方向跨度约2°，经度方向跨度约0.5°。

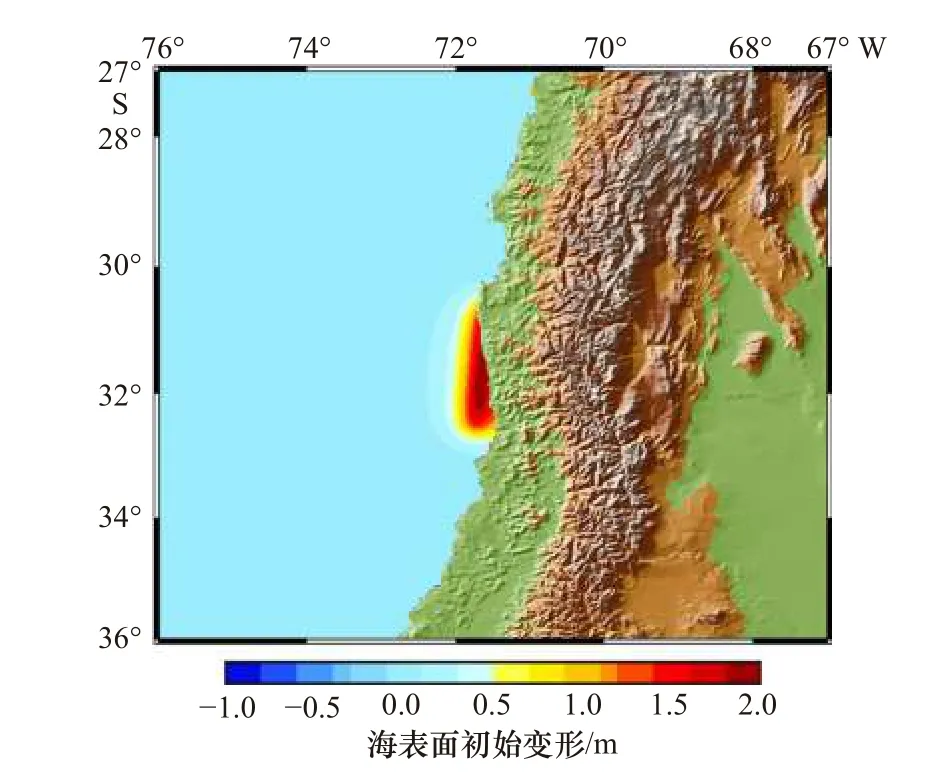
图3 地震引起的海表面初始变形Fig. 3 Initial sea surface deformation induced by the earthquake

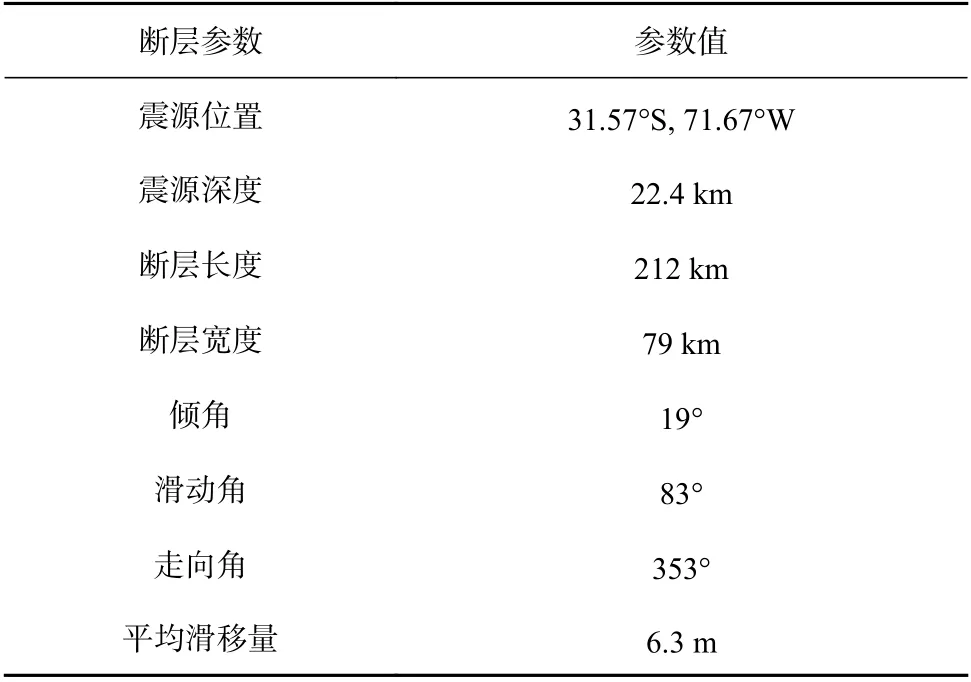
表1 智利地震断层参数Table 1 Fault parameters of Chile earthquake

4.2 智利海域区域海啸模拟

智利海域区域海啸模拟范围为60°S～5°N、65°～110°W，地形数据来自ETOPO1 (https://www.ngdc.noaa.gov/mgg/global/global.html)，其中以平均海平面为基准，海域水深为负、陆地为正。模型采用分辨率为1′的均匀网格，时间步长Δt=2 s，整个模拟过程为8 h（图4）。Manning 系数在水深小于100 m 时取0.025，其余则取0。计算域四周设置为开放边界。本文模拟采用CPU 为Intel(R) Core(TM) i7-7500U 的笔记本电脑，整个模拟耗时50.5 h。

为了验证结果，本文选取了14 个智利近岸测站的实测数据（各测站位置见图4）。模拟结果与测站实测比较见图5，各测站第一个测到的海啸先导波时间与波幅比较见表2。模拟与实测的海啸先导波到达时间及波幅均吻合良好。智利海域的海啸持续时间较长，且实测相较于模拟结果呈现出更多的微小波动现象，这可能是由于近岸剧烈变化的地形及岸线影响。此外，COQUIMBO 测站所测最大波高达4.75 m，最大波不是先导波，且先导波后的几个波幅基本超过2.5 m，大于模拟结果。其可能的原因一方面是该测站位于震源附近，受复杂的地震影响，概化的海啸源模型没有充分反演海啸产生阶段一系列复杂的过程。另一方面是该测站所处位置地形变化剧烈，模型采用的网格未能精细刻画地形。

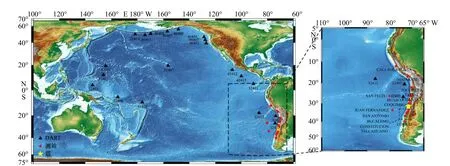
图4 智利区域海啸和泛太平洋海啸模拟范围及DART 浮标与智利近岸测站位置Fig. 4 Domains of Chile regional tsunami and the Pacific tsunami and the location of DART buoys and coastal tide-gauge stations

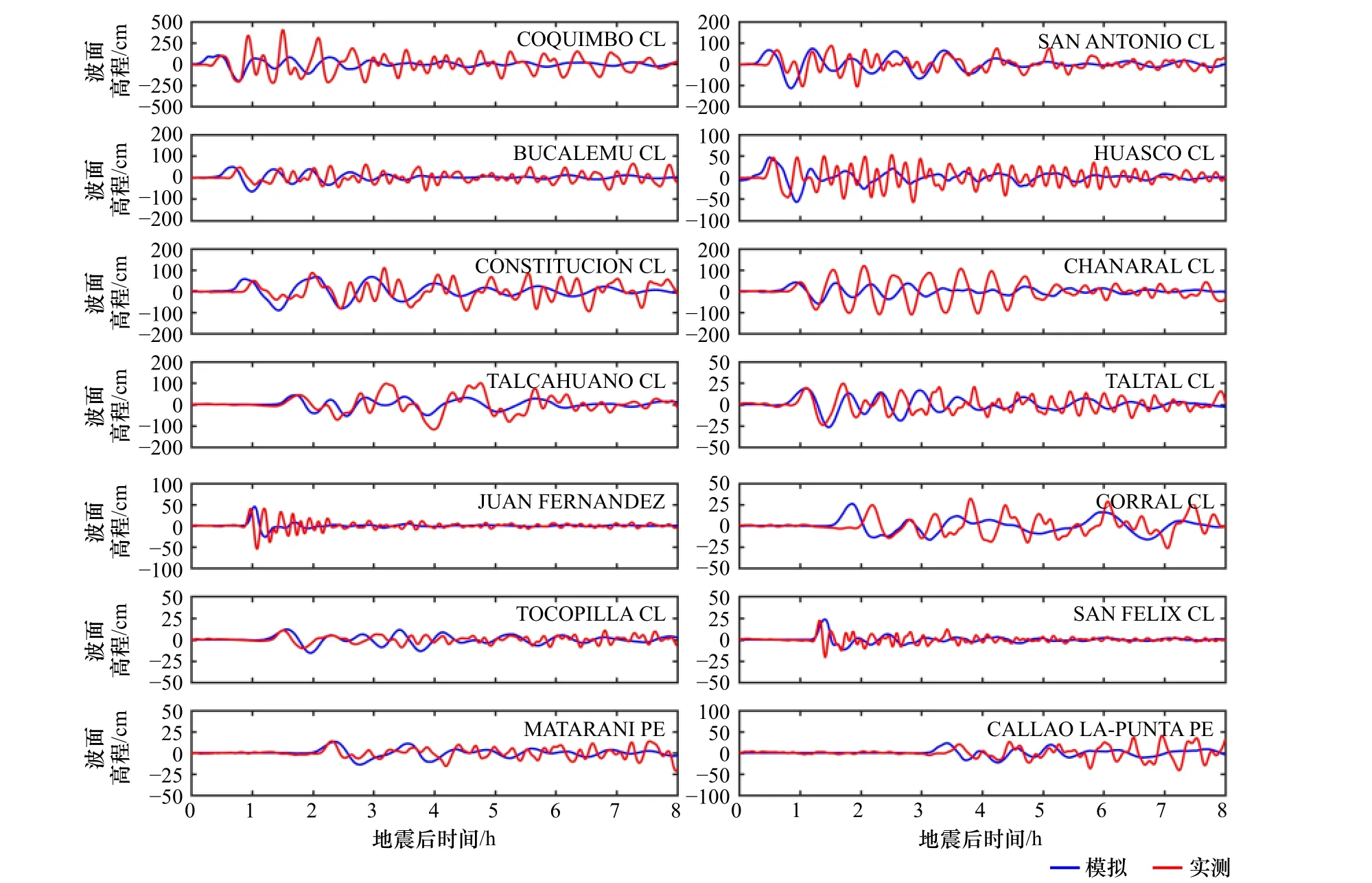
图5 智利近岸测站波面过程与模拟对比Fig. 5 Time histories of observation and simulation at Chile coastal tide-gauge stations

表2 智利近岸测站海啸先导波到达时间和波幅模拟与实测比较Table 2 Comparisons of simulation and observation of the arrival time and amplitude for the leading wave at Chile coastal tidal-gauge stations

4.3 泛太平洋海啸模拟

泛太平洋海啸模拟区域为75°S～70°N，100°E～60°W，地形数据同样来自ETOPO1，采用空间分辨率为4′的均匀网格。Manning 系数与4.2 节区域海啸相同，计算域四周均为开放边界。模拟时间步长Δt=5 s，整个模拟过程为25 h，同样采用CPU 为Intel（R）Core（TM）i7-7500U 的笔记本电脑，用时28.0 h。

地震发生后不同时刻的瞬时波面过程见图6，第一个出现的海啸先导波到达时间见图7。海啸传播初期基本以震中为圆心向四周扩散（图6a）。当海啸经过海脊和海底山等地形时，由于其在水深较浅的地区传播速度变慢，导致海啸波峰线呈现V 形，即在海脊和海底山附近的海啸波传播较慢而在深水处传播较快。由于太平洋NE 侧水深较SW 一侧深，所以海啸波峰线逐渐从NE-SW 方向变化至SN 向（图6d），其对应的先导波到达时间也呈现出NE 侧快于SW 侧的特点（图7）。此外，太平洋SW 侧存在众多海脊、海底山及海岛，导致此处的海啸波较NE 侧呈更加复杂的波面过程。

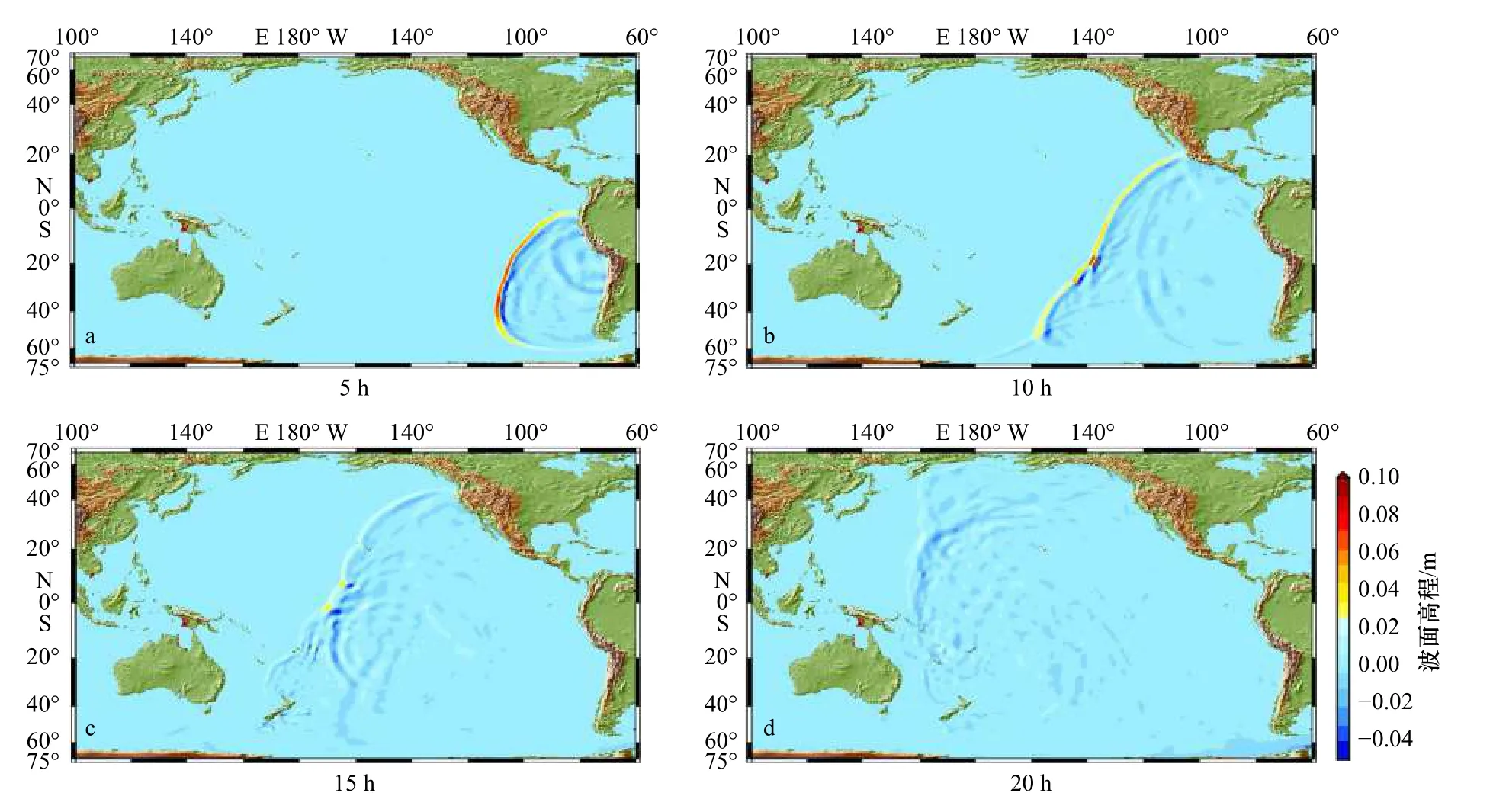
图6 地震后越洋海啸瞬时波面分布Fig. 6 Snapshots of simulated tsunami wavefields after the earthquake

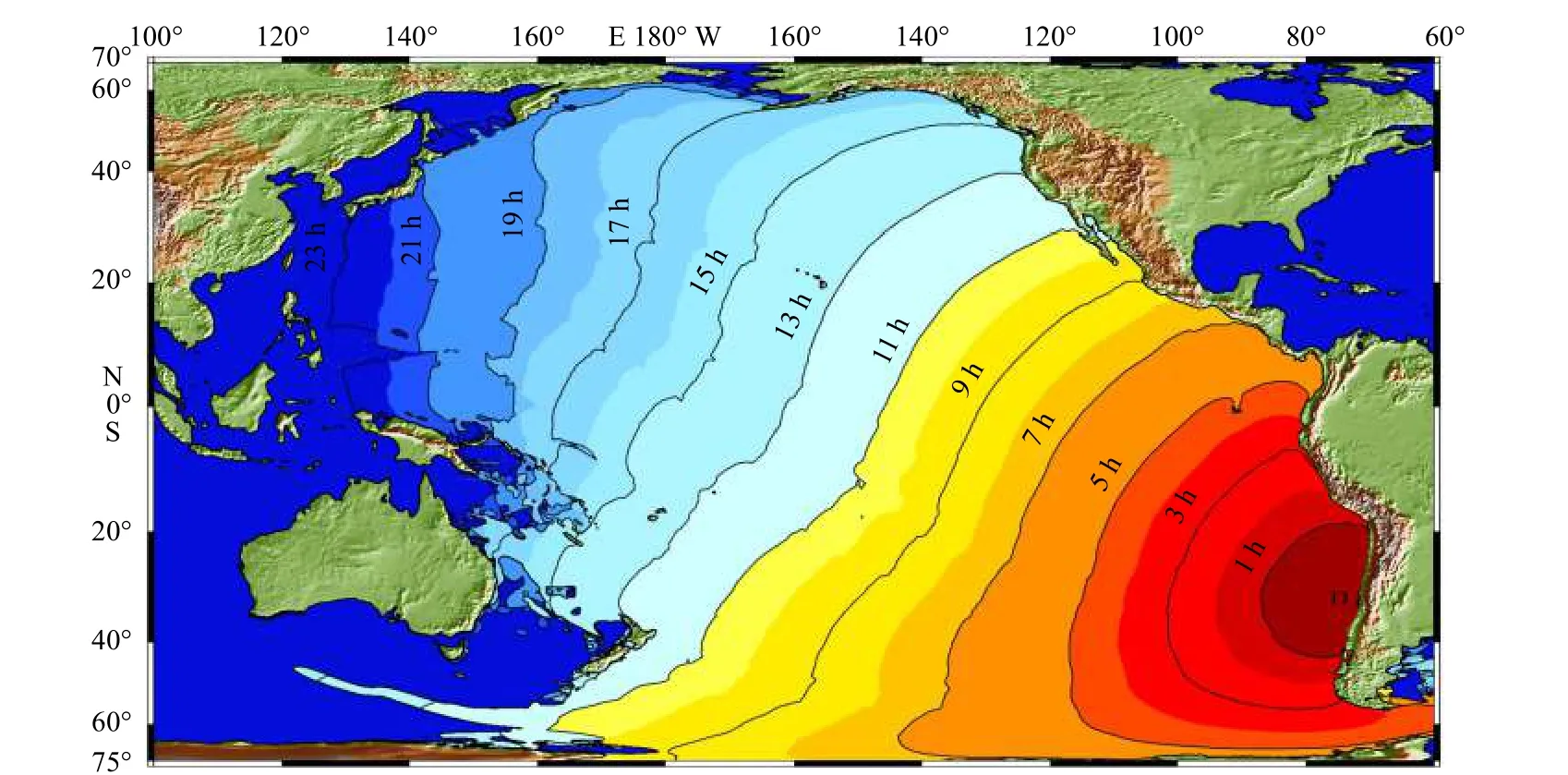
图7 海啸先导波到达时间等值线图Fig. 7 Contours of the arrival time for the leading tsunami wave

进一步选取20 个分布于环太平洋沿岸及位于太平洋中部的DART 浮标（见图4）验证本文所建立的数值模型，其中波面过程对比见图8、海啸先导波的到达时间和波幅对比见表3。由于从智利至太平洋东北侧的海域地形相对规则，海啸最大波通常为其先导波，且波形规则、持续时间较短。该海域的海啸模拟结果与实测吻合较好。相比于东北侧，太平洋西南侧的地形复杂，存在着海脊、海底山和海岛等地形。海啸在此受海底地形折射、绕射等影响，自由水面呈较为复杂的波动过程，海啸最大波不再是先导波。该海域本文模拟的前几个波动过程与实测基本吻合，但后续的波动过程无论在振幅还是相位上均存在一定差别。这可能是由于模型采用的网格未能精细刻画出该区域复杂的地形所致。

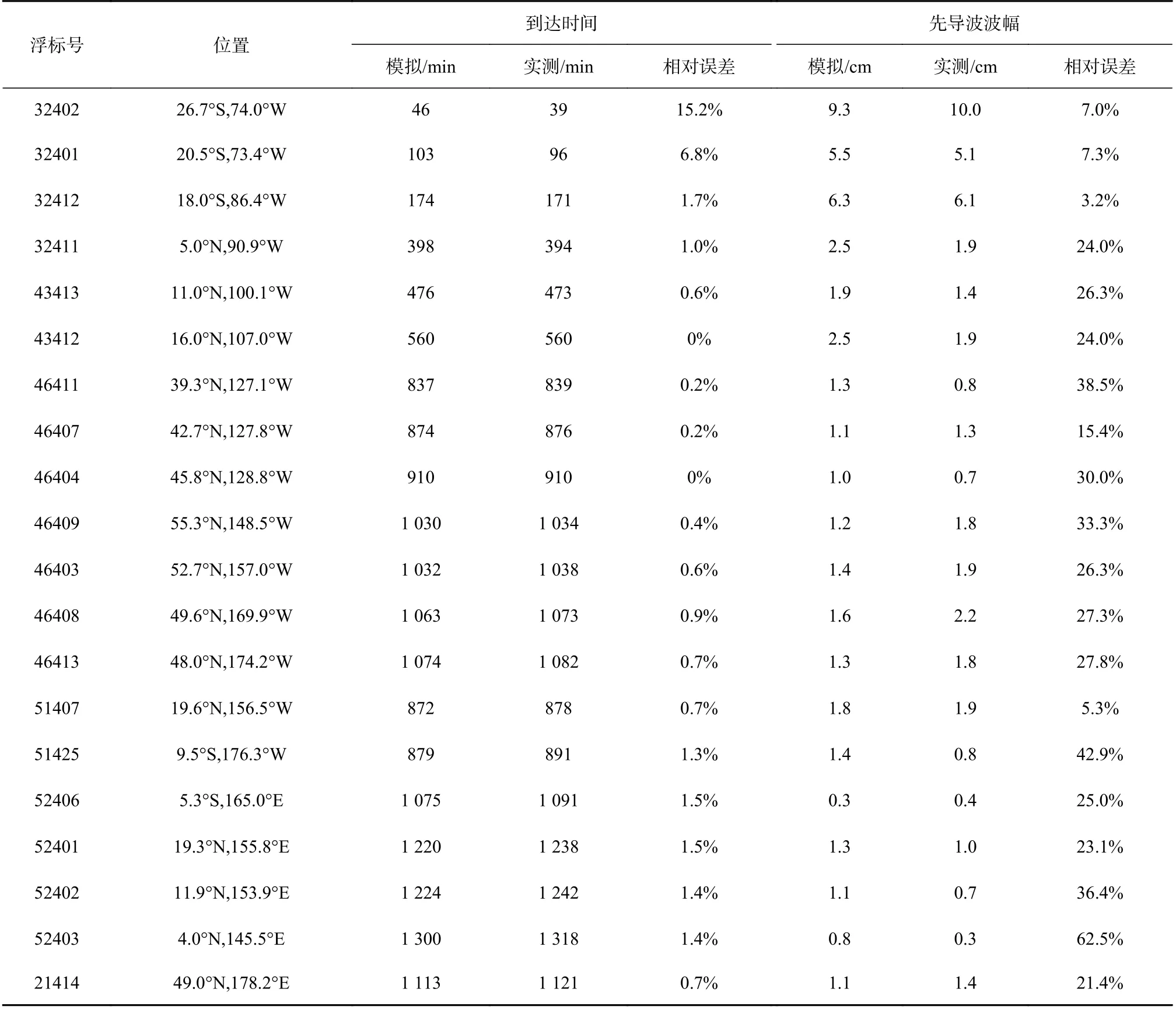
表3 DART 浮标海啸先导波到达时间和波幅模拟与实测比较Table 3 Comparisons of simulation and observation of the arrival time and amplitude for the leading wave at DART buoys

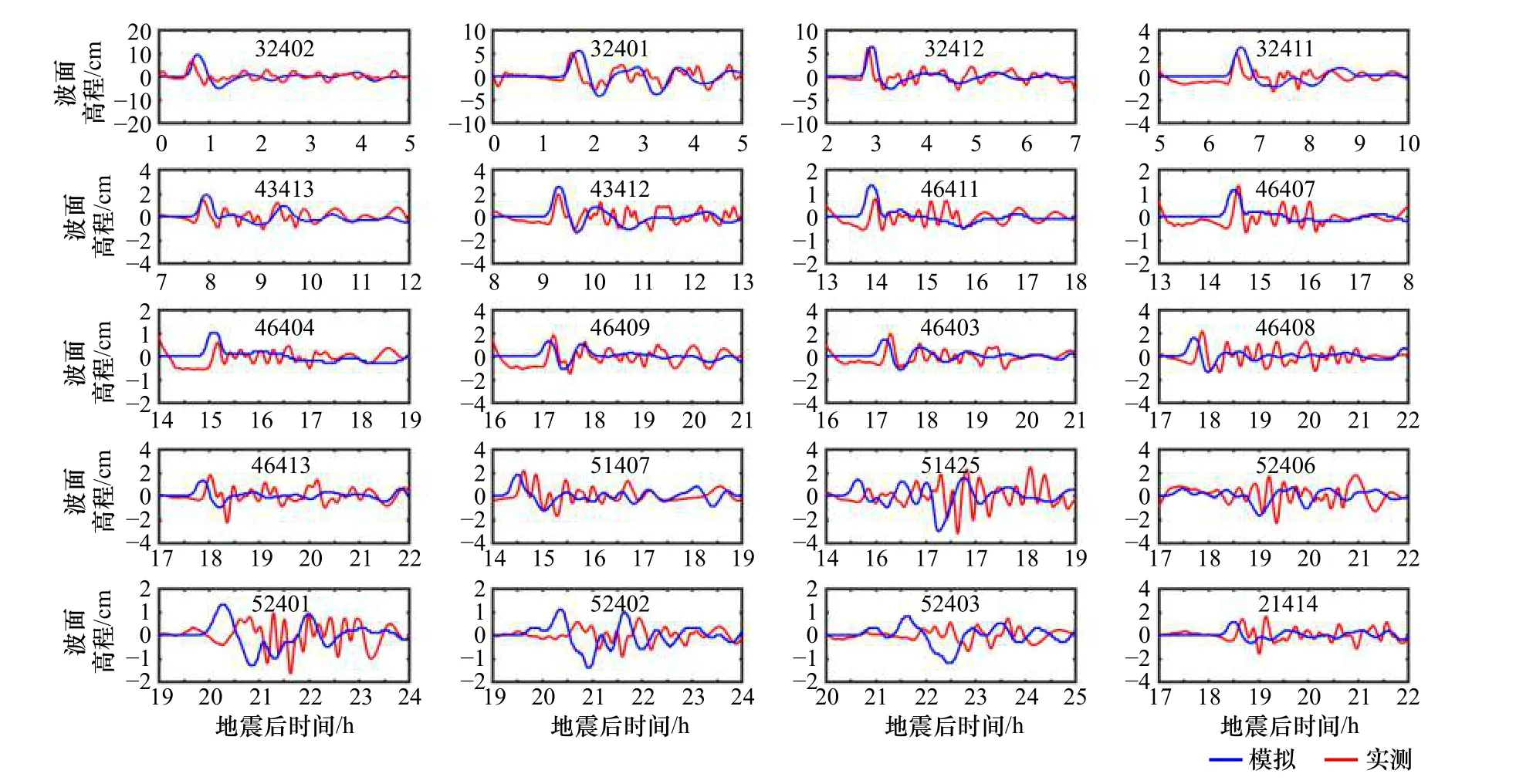
图8 DART 海啸浮标实测波面过程与模拟结果对比Fig. 8 Comparisons of the free surface elevation between DART buoys and simulations

本文模拟的海啸先导波到达时间与实测结果随着传播距离增加其误差也逐渐增加，这可能是由于海啸波的频散效应所致。Glimsdal 等[34]提出一个与传播距离和时间呈正相关的“频散时间”以量化海啸的频散效应。这与本文模拟结果所显示的随着海啸传播距离和时间的增加先导波到达时间的误差逐渐增加是一致的。此外，实测资料显示在海啸较大波动到达之前会有一段幅度较小的减水过程，Watada 等[35]认为其与海底的弹性形变有关。由于本文的模型没有考虑该因素的影响，未能真实反演这一物理现象。

图9 为智利海啸在太平洋的最大波幅分布。在智利附近海域，海啸最大波幅主要受断层走向影响，呈现出由智利沿岸向西扩散的趋势。在距离震源较远的区域，海啸最大波幅呈现由智利向日本延伸的趋势，且基本与海脊走向一致，这可能是海啸在海脊上形成所谓的海脊俘获波所致[36]。

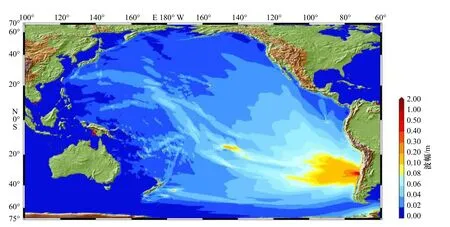
图9 智利海啸在太平洋的最大波幅分布Fig. 9 Distribution of maximum wave amplitude in the Pacific for Chile tsunami

5 结论

本文基于球坐标系下的全和谐型浅水方程，采用MUSCL-Hancock 格式，并利用HLLC Riemann 近似求解器计算单元界面上的流体通量，最终建立了二阶精度的Godunov 格式有限体积海啸数值模型。由于近岸局部地区海啸淹没爬坡的精细化模拟和受灾评估中必将涉及到干湿边界的处理；同时，良好的干湿边界处理还有益于维持越洋海啸模拟的稳定性，因此，本文建立的模型包含了处理干湿边界的功能。在此基础上，本文利用弹性半空间位错理论得到的初始自由水面模拟了2015 年9 月16 日智利Mw8.3 级地震引发的区域海洋和泛太平洋海啸传播过程。分别通过与智利近岸14 个测站和环太平洋20 个DART 浮标实测数据比较，进一步验证了模型模拟实际海啸过程的能力。

本文泛太平洋海啸的模拟采用空间分辨率为

4′的均匀网格，在开阔海域和水深变化较缓的区域模拟结果与实测吻合良好，然而在一些岛屿及近岸受复杂地形及岸线影响的区域有一定误差，主要是由于模拟所采用的网格空间分辨率未能精细刻画这些因素的影响。为了兼顾实际模拟中的精度与效率，今后将在控制方程中考虑海水的压缩性、地震导致的海底弹性形变等因素的影响并结合多层嵌套与并行技术进一步提高模型的模拟能力。