迭代运算使不连续映射变为光滑映射

刘晓华，罗天琦

1.乐山师范学院 数理学院，四川 乐山 614000；2.乐山师范学院 教师教育学院，四川 乐山 614000

迭代运算是数学中的重要运算之一，它在许多复杂的问题，如分岔、混沌和分形[1-3]问题、多项式[4-8]、拟多项式[9-10]、线性分式[11]和有理函数[12]等问题中有广泛的应用.在一维的情况下，高次迭代的计算也是一项复杂的工作.随着C0映射迭代理论的发展[13-14]，人们也逐渐开始研究不连续映射或者集值映射等“坏映射”的迭代和它们的迭代根[15-18].

通常，人们认为一个“坏映射”可能会通过迭代运算变得更加复杂，但文献[19]表明不连续的自映射通过迭代运算可能变为连续的自映射，并给出了在紧区间上只有一个间断点的分段C0自映射的二次迭代连续性的充要条件.文献[20]进一步研究了在紧区间上只有一个非光滑点的连续自映射二次迭代的光滑性，并给出了它们的二次迭代是C1光滑映射的充要条件.文献[20]的工作不是对文献[19]的工作的重复，因为文献[20]所考虑的映射的导数可能不是自映射.综合文献[19-20]，我们可以判断在紧区间上只有一个间断点的分段C1自映射四次迭代的C1光滑性.但是我们还不能判断：在紧区间上什么不连续的自映射的二次迭代不仅连续而且C1光滑? 例如，自映射

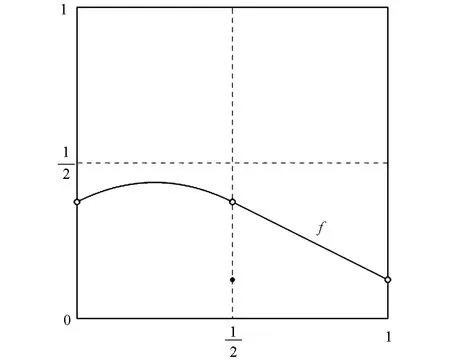
图1 f有一个可去间断点

在(0，1)上是C1光滑的(图2).

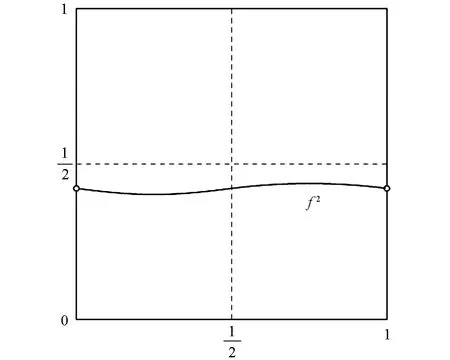
图2 f2在(0，1)上是C1光滑的

本文研究在区间I=(0，1)上只有一个可去间断点的所有分段C1自映射Vr(I，I).每个f∈Vr(I，I)能被表示为

(1)

其中，x0∈(0，1)是f唯一的可去间断点，f1和f2分别在I1和I2上是C1光滑的，c∈(0，1)是一个常数.为了研究在Vr(I，I)中映射的二次迭代的光滑性，我们需要将Vr(I，I)分成一些子类，即Vr(I，I)=Vrr(I，I)∪Vrj(I，I)∪Vro(I，I)∪Vr∞(I，I)，其中：

本文讨论Vr(I，I)中映射的二次迭代的C1光滑性.首先给出了在Vrτ(I，I)中映射的二次迭代是C1光滑映射的充要条件，其中τ∈{r，j，o}，获得了在Vr∞(I，I)中映射的二次迭代是C1光滑映射的必要条件.其次说明了找Vr∞(I，I)中映射的二次迭代是C1光滑映射的充分条件的困难.最后用例子展示了在Vr(I，I)中映射的二次迭代是C1光滑映射的条件.

下面讨论由(1)式定义的f∈Vr(I，I)的二次迭代的光滑性.记

(2)

为了方便，记

Crr(I，I)={f∈Vrr(I，I)|f(y0)=Γ(c)}

Crτ(I，I)={f∈Vrτ(I，I)|f(y0)=Γ(c)和f′(y0)=0}τ∈{j，o，∞}

我们用D+f和D-f分别表示f的右导数和f的左导数.

定理1假定f∈Vrτ(I，I)由(1)式定义，其中τ∈{r，j，o}，且f有唯一的间断点x0∈(0，1).令y0由(2)式定义.那么，f2在I上是C1光滑的当且仅当y0∈Ii，f(I1∪I2)⊆Ii成立(i=1，2)和f∈Crτ(I，I).

证首先证明必要性.假定f2在I上是C1光滑的，那么f2在I上是连续的.由文献[19]的定理1知，y0∈Ii，f(I1∪I2)⊆Ii和

f(y0)=fi(y0)=Γ(c)

(3)

其中i=1，2.在下文中，我们只讨论y0∈I1和f(I1∪I2)⊆I1的情况，因为y0∈I2和f(I1∪I2)⊆I2情况的讨论与y0∈I1和f(I1∪I2)⊆I1情况的讨论是完全类似的.下证在y0∈I1和f(I1∪I2)⊆I1的情况下，有

(4)

假设f∈Vrτ(I，I)，其中τ∈{r，j，o}.

情形1f∈Vrr(I，I).由(3)式和Crr(I，I)的定义，我们知道f∈Crr(I，I).

情形2f∈Vrj(I，I).由Vrj(I，I)的定义，我们有

由(4)式得到f2在x0的左导数和右导数分别为

(5)

(6)

(7)

由(3)，(7)式和Crj(I，I)的定义，我们知道f∈Crj(I，I).

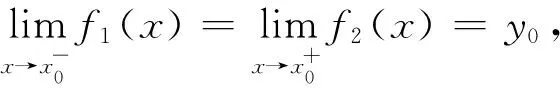
(8)

(9)

注意到

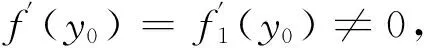
其次证明充分性.我们仅证明y0∈I1，f(I1∪I2)⊆I1的情况.

当f∈Crr(I，I)时，由Crr(I，I)的定义有f(y0)=f1(y0)=Γ(c)和f∈Vrr(I，I).由文献[19]的定理1知f2在I上是连续的.因为f∈Vrr(I，I)，则

由(4)式能获得(5)式和(6)式，则D-f2(x0)=D+f2(x0).因此，f2在I上是C1光滑的.

综上所述，f2在I上是C1光滑的.

定理2假定f∈Vr∞(I，I)由(1)式定义，x0∈(0，1)是f的唯一间断点.令y0由(2)式定义.假设f2在I上是C1光滑的，则y0∈Ii，f(I1∪I2)⊆Ii(i=1，2)，且f∈Cr∞(I，I).

证证明方法与定理1中f∈Vro(I，I)的必要性的证明完全类似.

其中

图3 F1有唯一可去间断点

其中

它在(0，1)上是C1光滑的(图4).

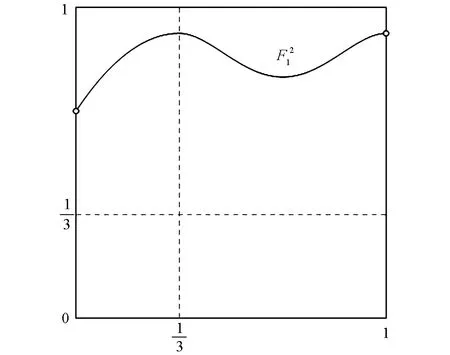
图在(0，1)上是C1光滑的

图5 F2有唯一的可去间断点

而且

则F2∈Vro(I，I).注意到

它在(0，1)上是C1光滑的(图6).

图在(0，1)上是C1光滑的

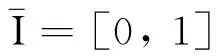
在这篇文章中，我们仅考虑了(1)式定义的映射唯一的间断点是可去间断点的情形，对(1)式定义的映射唯一间断点是跳跃或者振荡间断点的情形，我们将在后续文章中加以研究.