曳引式电梯垂直振动分析

严文磊 薛大猛

1盐城工学院 盐城 224000 2希姆斯电梯（中国）有限公司 无锡 214000

0 引言

根据国家市场监管总局特种设备局统计，截至2019年底，注册在运行的电梯总量达到709.75万台，当年新增81.92万台。电梯已经同人们日常生活息息相关，成为不可缺少的一部分。

振动加速度是电梯乘运质量的关键评价指标之一，GB/T 10058—2009《 电梯技术条件3.3.5中规定乘客电梯轿厢运行在恒加速度区域内的垂直（Z轴）振动的最大峰峰值不应大于0.3 m/s2，A95峰峰值不应大于0.2 m/s2。本文通过对试验塔内某台电梯进行动力学分析，找出影响振动加速度的关键因素。

1 动力学建模

试验塔内电梯梯速为2.5 m/s，额定载重为1 600 kg，曳引比为2:1，轿厢质量为750 kg，轿架质量为700 kg，对重质量为2 250 kg，曳引机质量为480 kg，钢丝绳根数为7根，直径为0.01 m，线密度为0.407 kg/m，弹性模量为8×1010Pa，绳头弹簧刚度为2.12×105N/m，轿底减震橡胶刚度为5×105N/m，曳引轮，对重轮和导向轮直径为0.4 m。其结构见图1。

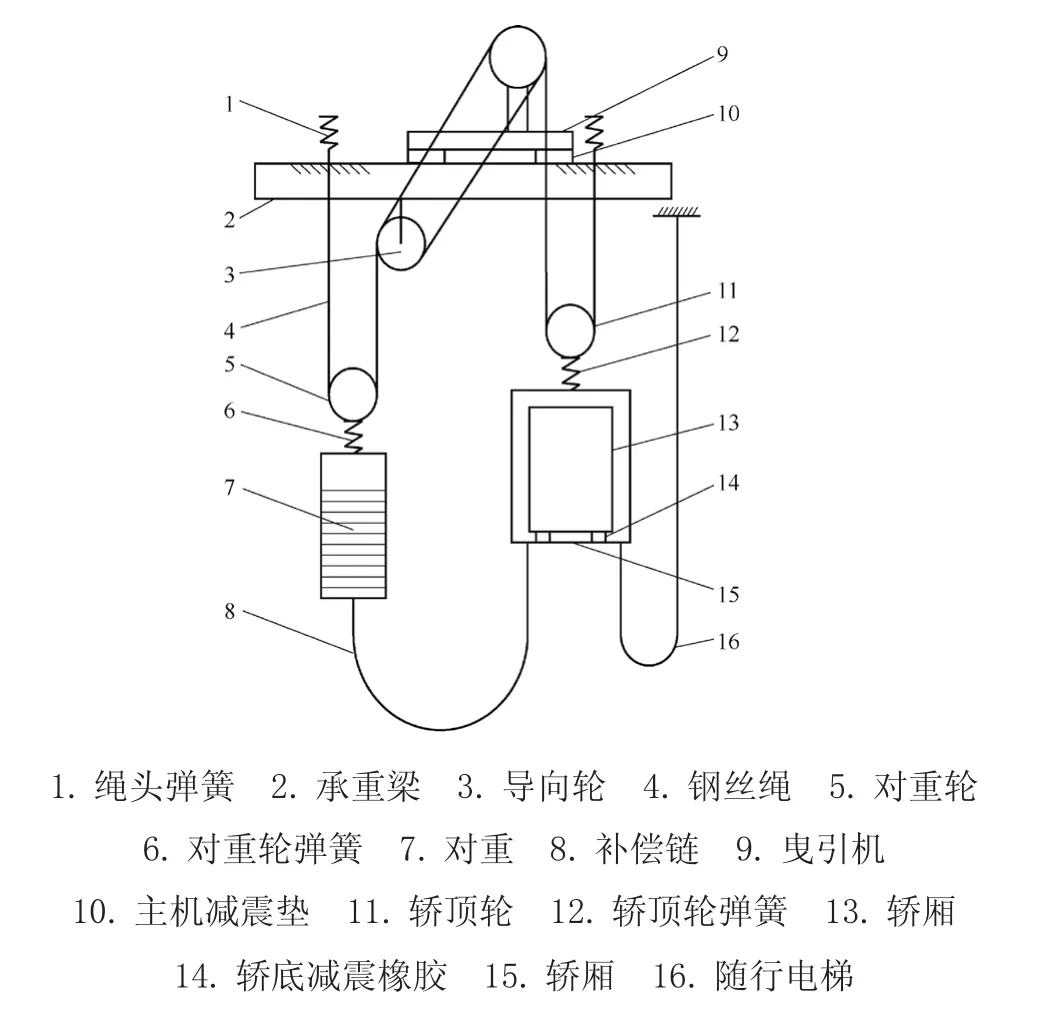
图1 电梯结构示意图

假定位移向上为正方向，角位移逆时针为正，对电梯建立动力学模型，其动力学模型见图2。

图2 电梯动力学模型

在图2中，m1为轿厢和额定载荷质量，m2为轿架和部分补偿链、随行电缆等效质量，m3为对重和部分补偿链等效质量，m4为曳引机和导向轮等效质量，I1为曳引轮和导向轮等效转动惯量，r1为曳引轮半径，m5轿顶轮和钢丝绳等效质量，I2为轿顶轮转动惯量，r2为轿顶轮半径，m6为对重轮和钢丝绳等效质量，I3为对重轮转动惯量，r3为对重轮半径，k1为轿底减震橡胶等效刚度，c1为轿底减震橡胶阻尼，k2为轿顶轮弹簧等效刚度，c2为轿顶轮弹簧阻尼，k3为对重轮弹簧等效刚度，c3为对重轮弹簧阻尼，k4为承重梁和主机减震垫等效刚度，c4为承重梁和主机减震垫阻尼，kr1为轿顶轮到绳头弹簧之间钢丝绳和绳头弹簧的等效刚度，cr1为轿顶轮到绳头弹簧之间钢丝绳和绳头弹簧的阻尼，kr2为轿顶轮到曳引机之间钢丝绳等效刚度，cr2为轿顶轮到曳引机之间钢丝绳阻尼，kr3为对重轮到曳引机之间钢丝绳等效刚度，cr3为对重轮到曳引机之间钢丝绳阻尼，kr4为对重轮到绳头弹簧之间钢丝绳和绳头弹簧的等效刚度，cr4为对重轮到绳头弹簧之间钢丝绳和绳头弹簧的阻尼，kT为曳引机的扭转刚度，cT为曳引机阻尼。

参考文献[2]认为，当电梯提升高度大于50 m时，钢丝绳自重对垂直振动影响较大，需要考虑其质量，而当提升高度较低时，钢丝绳质量可以忽略不及。参考文献[3]通过计算发现，将钢丝绳离散成4段可以得到较为稳定的结果。为了考虑钢丝绳的质量，同时减少模型的自由度，本文通过对钢丝绳分布质量作近似计算，得到其等效质量。

设钢丝绳的长度为l，单位长度的质量为p，假定钢丝绳的变形与固定点的距离ξ正比，钢丝绳端点的位移为x，将微元长度dξ的动能在整个钢丝绳长度范围内积分，以计算钢丝绳的动能

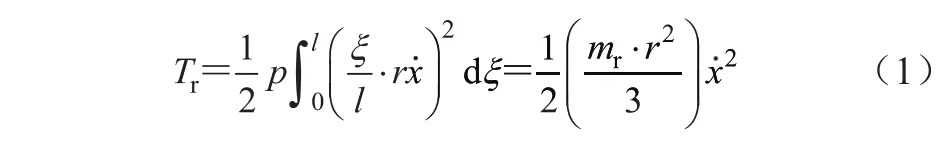
式中：mr为钢丝绳质量，mr＝pl，r为曳引比，mrr2/3为钢丝绳的等效质量，将其加到轿顶轮或对重轮上。钢丝绳分布质量系统见图3。

图3 钢丝绳分布质量系统

此外，参考文献[2]认为，曳引机－曳引轮之间为完全刚性传动，故曳引轮的扭转刚度为0。由于在模型中需使用此参数，整个系统会存在刚体模态，在矩阵分解时会造成计算困难，故取一个很小的数值。参考文献[3]认为当电梯采用有齿轮曳引机时，在曳引机输出轴到曳引轮轴之间有蜗轮蜗杆减速器，故两者之间非刚性传动，存在扭转刚度。当今的电梯中多采用永磁同步无齿轮曳引机，曳引机输出轴与曳引轮轴直接相连，没有减速器，故该过程可看作刚性传动，扭转刚度为0。为了避免计算困难，同样赋予其很小的数值。参考文献[5]认为，在电梯建模仿真过程中，如果抱闸处于释放状态，曳引轮可自由转动，故扭转刚度看作0。因此，在本文中的扭转刚度取10-6Nm/deg。

根据拉格朗日方程可得

式中：T为系统的动能，V为系统的势能，xi为系统第i个自由度的广义位移，为系统第i个自由度的广义速度，Qi为系统第i个自由度的广义力。

其中，系统的动能为

系统的势能为

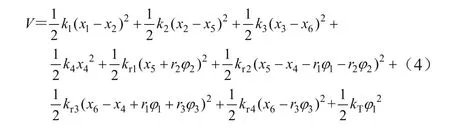
经过简化可以得到系统动力学方程

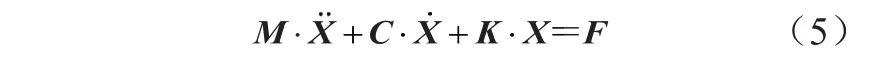
式中：M为系统的质量矩阵，C为系统的阻尼矩阵，K为系统的刚度矩阵，F为系统的激励力列阵，X··为系统的广义加速度列阵，X·为系统的广义速度列阵，X为系统的广义位移列阵。

由式（3）和式（4）得

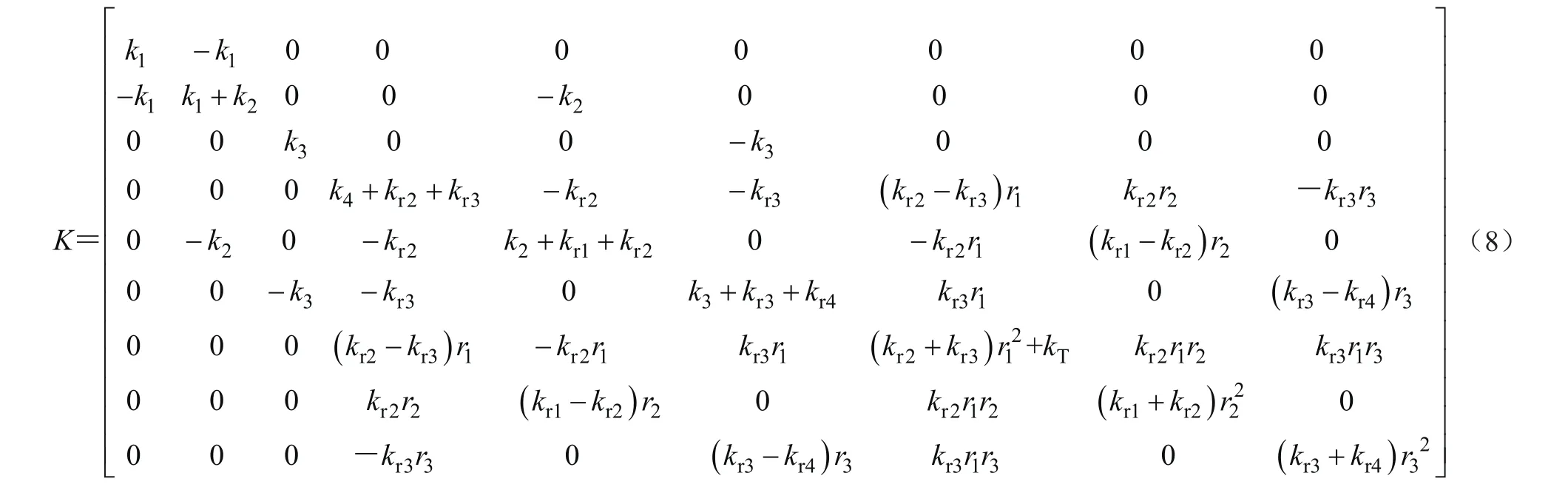
在工程中，电梯的实际阻尼难以测量，考虑到电梯为小阻尼机械系统，采用Rayleigh阻尼模型进行等效

式中：ac、bc为阻尼系数，参照文献[6]，取ac=0.01，bc=0。

考虑电梯系统运行中的惯性力和惯性力矩，曳引轮，对重轮、导向轮的旋转失衡，激励力列阵见式（10）。根据文献[7]中曳引轮偏心实验，将曳引轮偏心质量近似看作为1 kg，偏心距为0.15 m，轿顶轮及对重轮偏心质量近似看作为0.2 kg，偏心距为0.15 m。

式中：mt为曳引轮转子偏心质量，mj为轿顶轮转子偏心质量，md为对重轮转子偏心质量，ωt为曳引轮转动角速度，ωj为轿顶轮转动角速度，ωd为对重轮转动角速度；et为曳引轮偏心距，ej为轿顶轮偏心距，ed为对重轮偏心距，a为轿厢运行加速度。

2 模态分析

无外力作用的多自由度系统受到初始扰动后，即产生自由振动。其方程为

此方程的特解为

其中，Ф＝（φi）为各坐标振幅组成的n阶列阵，此特解表示系统内各个坐标偏离平衡值时均以同一频率ω和同一初相角θ做不同振幅的简谐运动。

系统的固有频率和振型化为矩阵K和M的广义特征值和特征向量的问题，即

由于电梯垂直方向动力学系统的平衡位置是随遇的，故主振动存在随时间无限增大的刚体位移。显然，系统的第一阶固有频率ω1＝0。通过模态分析，可求出电梯垂直振动系统的固有频率，从而避免外激励的频率与固有频率相同而形成共振。

在电梯空载时，求得二～六阶固有频率随时间的变化如图4～图8所示。

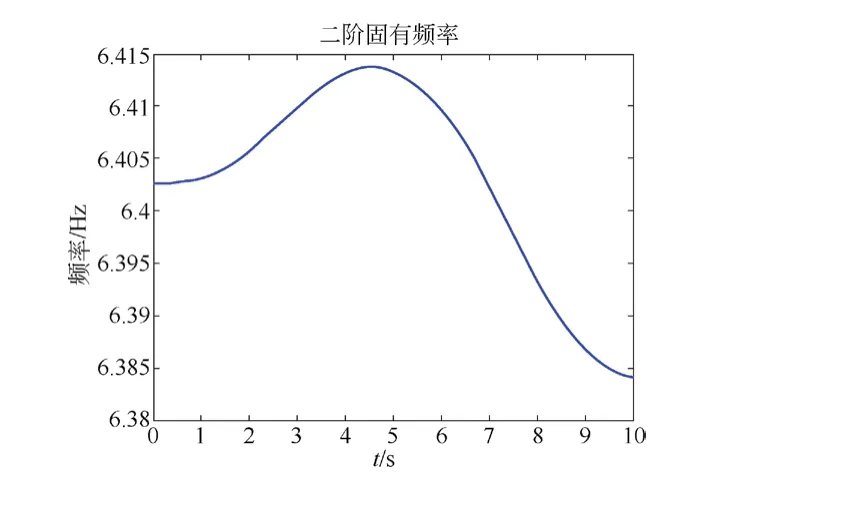
图4 空载电梯二阶固有频率

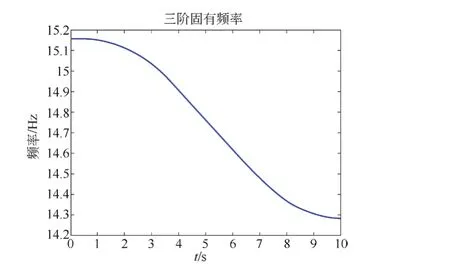
图5 空载电梯三阶固有频率

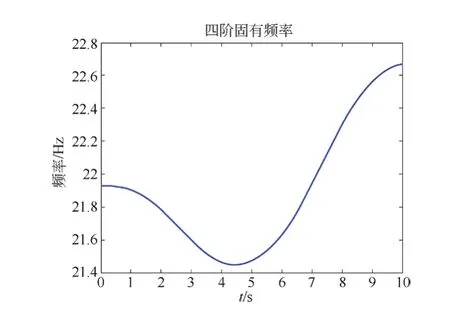
图6 空载电梯四阶固有频率

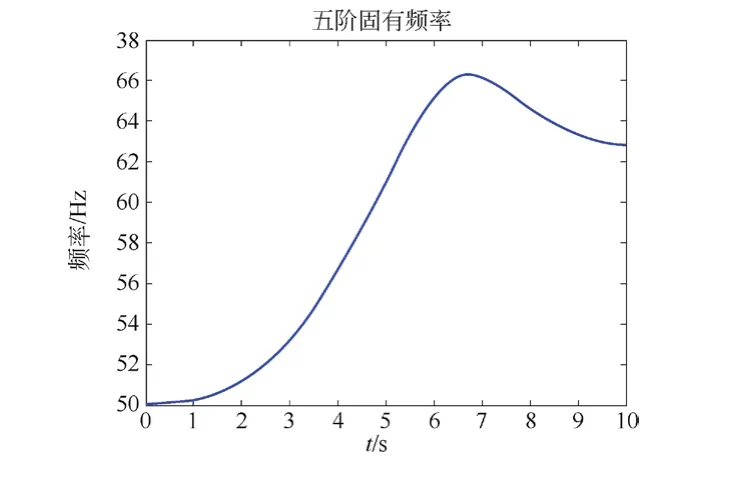
图7 空载电梯五阶固有频率

图8 空载电梯六阶固有频率

随着电梯上升，二阶固有频率从6.4 Hz先上升再下降，波动幅度约为0.5 Hz；三阶固有频率从15.1 Hz开始降低，降低幅度约为1 Hz；四阶固有频率从21.9 Hz先下降再上升，波动幅度约为1 Hz；五阶固有频率从50 Hz先上升再下降，波动幅度约为16 Hz；六阶固有频率从151 Hz开始先下降再上升，波动幅度约为60 Hz。

电梯二～四阶固有频率随着电梯上升波动幅度不大。从第五阶固有频率开始，波动范围大幅增加。在此系统中，曳引机振动频率约为3.98 Hz，故不会出现曳引机振动引起共振的情况。

3 动力学方程求解

对多自由度动力学方程的求解方法有多种，一般做法是将多自由度方程通过坐标变化解耦成单自由度方程，再基于振型叠加法使用杜哈梅积分求解，但这种解法繁琐且计算量大，本文中将通过Newmark-β法对多自由度方程求解。

Newmark-β法是一种数值分析方法，其基本原理是将时间离散化，在时间增量内假定加速度变化规律计算结构动力响应[8]。假设在ti和ti+1时刻的加速度值某一常量，记为a。有

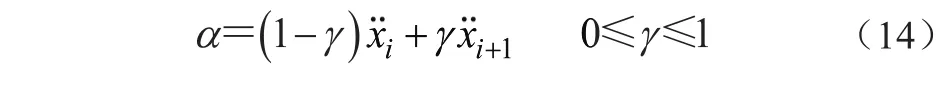
为得到稳定和高精度的算法，α也用另一控制参数β表示，即

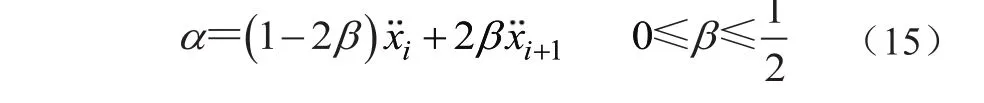
通过在ti到ti+1时间段上对加速度积分，可得ti+1时刻的速度和位移

将式（14）代入式（16），式（15）代入式（17）得

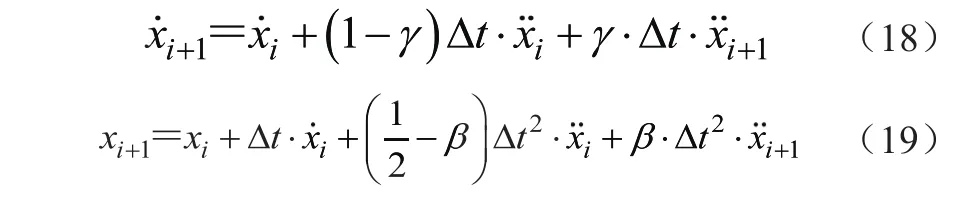
式（18）、式（19）为Newmark-β的两个基本递推公式，可解得ti+1时刻的速度和加速度的计算公式，即

由式（20）和式（21）所示的运动满足ti+1时刻的运动控制方程为

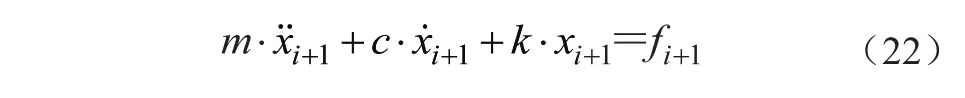
将式（20）和式（21）代入式（22）得ti+1时刻位移xi+1得计算公式为

其中

在Newmark-β法中，控制参数β和γ的取值影响算法的精度和稳定性，可以证明，只有当γ＝1/2时，该方法才具有二阶精度，故一般取γ＝1/2，β＝1/4。

4 测量及分析

使用EVA-625检测仪对试验塔内电梯进行测试，其轿厢实际速度和加速度曲线见图9、图10。

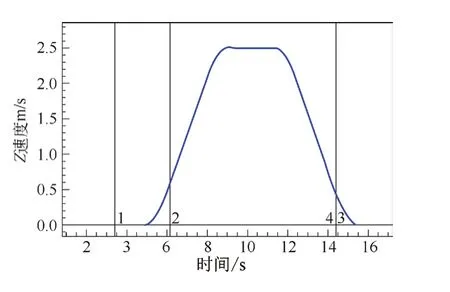
图9 实测速度曲线

由图10可知，电梯由启动到制停共分为7个时间段。其中，0～t1时刻，加速度a从0上升到最大值am；t1～t2时刻，加速度a保持恒定；t2～t3时刻，加速度a由am下降至0；t3～t4时刻，加速度a保持为0；t4～t5时刻，加速度a由0下降至-am；t5～t6时刻，加速度a保持为-am；t6～t7时刻，加速度a～-am上升至0。其中je为加加速度，vm为速度最大值[9]。电梯轿厢的速度和加速度可表示为

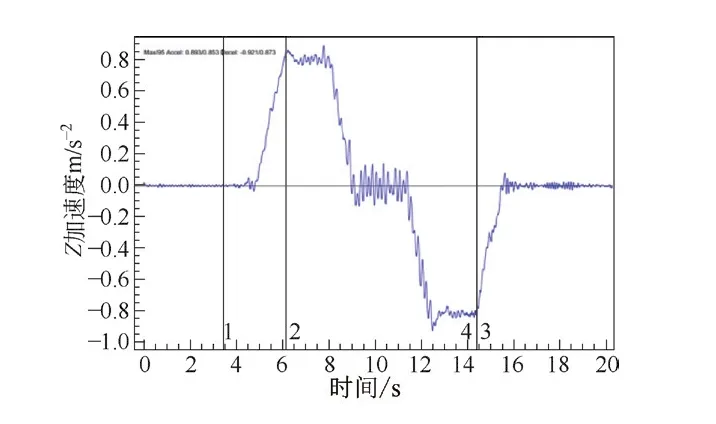
图10 实测加速度曲线

当je＝0.8 m/s3、am＝ 0.8 m/s2、vm=2.5 m/s时，模型的速度和加速度曲线见图11和图12。

图11 模型速度曲线

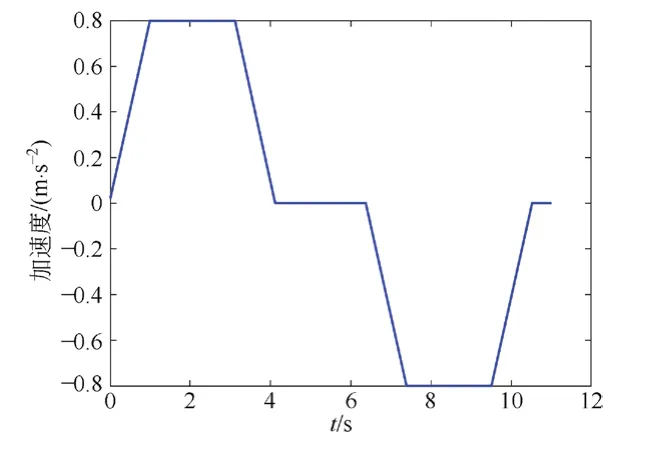
图12 模型加速度曲线

电梯轿厢在运行过程中，通过EVA-625检测仪对其垂直（Z轴）振动进行检测。其原始Z轴信号见图13。

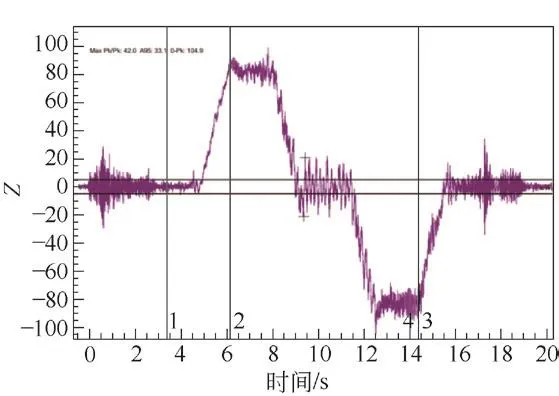
图13 原始Z轴信号

由图13可知，电梯启制动前后一段时间内，开关门机对信号影响甚大，应予以忽略。根据GB/T 24474—2009《电梯乘运质量测量》5.2.1中规定[10]：加速度和减速度值应通过对原始Z轴信号进行10 Hz低通滤波后计算。其滤波后的信号见图14。

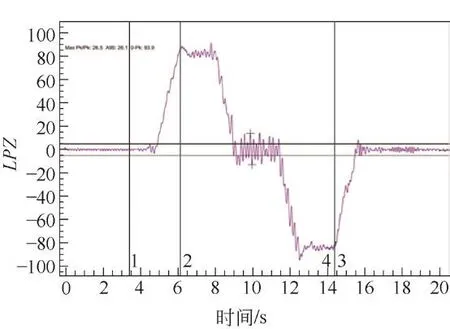
图14 10 Hz滤波后Z轴信号

由图14可知，可知其振动加速度最大峰峰值为0.265 m/s2，A95 峰峰值为 0. 261 m/s2。

EVA-625检测仪有3种滤波方式：ISO、高通和低通。其中ISO滤波器是振动分析中最有力的一个工具。ISO滤波器会依据IS08041标准将测试数据处理成标准中描述的人类能感受的垂直和水平方向的振动[11]。经过ISO滤波后的振动曲线如图15所示。

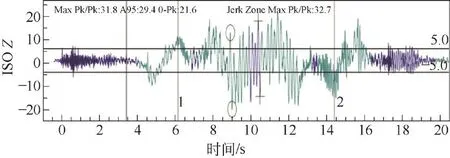
图15 ISO滤波垂直（Z轴）振动曲线

对经过ISO滤波后的最大峰峰值进行FFT（快速傅里叶转换）分析，可以得到振动的振幅和频率数据信息，快速傅里叶转换后见图16。为对比不同速度对电梯垂直系统固有频率的影响，在其他条件不变的情况下，将速度从2.5 m/s改为1.75 m/s，其最大峰快速傅里叶转换后见图17。

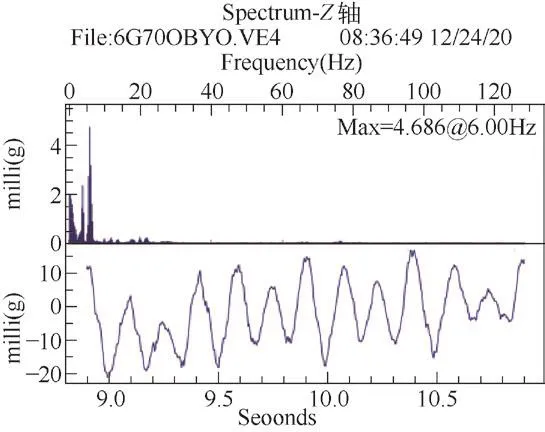
图16 2.5 m/s最大峰快速傅里叶转换

从图16和图17可以看出，对振幅影响最大的频率为6 Hz，与上文模态分析中系统的第二阶模态基本吻合，并且不随速度而变化。在图16中，频率4 Hz对振幅影响较大，这是曳引机振动的频率。此外的一些低频信号，可能是由电梯系统变刚度引起的自激振动[12]，也可能由电梯运行时空气阻力引起的振动[13]。

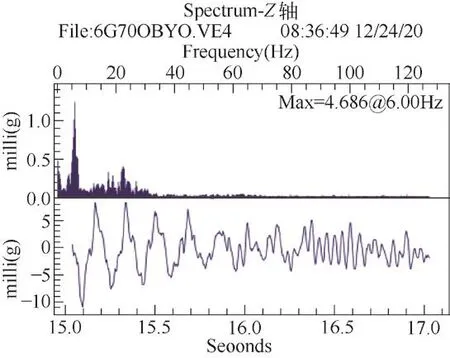
图17 1.75m/s最大峰快速傅里叶转换

通过Newmark-β法对动力学方程进行求解，可知其振动加速度峰值约为0.3 m/s2，高出实际测量值12%左右。模型中峰值加速度出现在变减速开始的阶段，而实测中峰值加速度出现在变加速结束的阶段，两组值相差不大。经过多次实验，发现其峰值加速度出现的位置很大程度上取决于现场实际情况。考虑到计算时做了部分假设和简化，故其值在实际工程中可以接受。Newmark-β法振动曲线见图18。

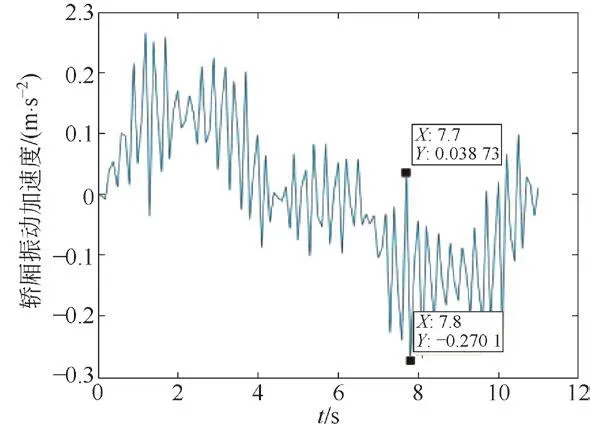
图18 Newmark-β法计算振动曲线

5 结论

综上所述，在不同速度下电梯系统的基频是不变的，且为振动的最主要成分。若基频发生变化，可能是电梯发生共振所致。当电梯发生共振时，可通过改变减震垫和绳头弹簧等的刚度改变系统固有频率以避免共振。

通过更改模型的参数，可知当曳引比为2:1时，反绳轮中存在的偏心质量，将对振动加速度产生相当大的影响；降低钢丝绳的弹性模量，可整体降低振动加速度；适当增加轿厢或者轿架的质量可有效降低振动加速度。