基于群体竞争遗传算法的带时间窗车辆路径规划

摘 要：为了提升传统遗传算法的寻优能力，本文提出了基于群体竞争的遗传算法，并从算法设计上说明了其寻优速度提升、不容易陷入局部最优的原因;将基于群体竞争的遗传算法应用于复合函数最大值的求取上，并对比传统遗传算法的寻优结果，结果发现前者寻优速度快;最后将算法应用于基于时间窗的车辆路径规划上，并得出了最优解。

关键词：群体竞争遗传算法;时间窗;车辆路径规划

中图分类号：TU443文献标识码：A文章编号：1003-5168（2021）04-0016-04

Abstract： In order to improve the optimization ability of traditional genetic algorithms， this paper proposed a genetic algorithm based of group competition， and explained the reason why its optimization speed increased and it was not easy to fall into a local optimum from the algorithm design; applied the genetic algorithm based on group competition to the maximum value of the compound function， and compared with the optimization results of the traditional genetic algorithm， found that the former was fast; finally applied the algorithm to the vehicle path planning based on time window， and obtained the optimal solution.

Keywords： genetic algorithm of group competition;time window;vehicle path planning

将人或者动物身上的奥秘进行解码，并应用于科学实践，一直是科学家的梦想。现在，很多成果已经被普及，其在智能化算法应用上的表现尤为突出，如遗传算法、免疫算法、蚁群算法、神经网络算法和模糊算法等[1-2]。遗传算法在系统寻优上存在绝对优势，所以被越来越多地应用于路径规划上。

达尔文的《物种起源》对遗传进化的思想进行了阐述，指出了微小概率的变异经过优胜劣汰的自然选择，最后会引发群体的集体进化。这种进化思想被美国人霍兰德成功应用于寻优算法，遗传算法就此诞生。

1 基于群体竞争的遗传算法

遗传算法需要先对所求解的问题进行编码，把求解空间编码成二进制或者十进制的字符串，表示可行解的空间，其最终目的是应用于计算机的求解[3-5]。每一个由二进制或者十进制组成的编码串可以看作是一个个体，个体中的每位二进制或者十进制称为基因。在算法运行之初，先随机产生多个个体，称为种群。遗传算法的搜索过程是基于选择、交叉和变异的。每一个个体是否优秀是需要有一个适应度函数来作为评价依据的，选择的目的就是要留下适应度较高的个体，淘汰适应度较低的个体。交叉的作用是以一定的概率选择群体中的两个個体，交换它们之间的几个基因。变异是以一定的概率选择其中的个体，对其某个基因进行一次改变。选择保留了每一代中的优秀个体，交叉保证了优秀基因可以转移，从而扩大了检索空间，变异的目的在于避免陷入局部最优而无法跳出。遗传算法的改良一般是在选择、交叉、变异的方式上进行改良。基于群体竞争的遗传算法主要操作过程如下。

1.1 编码

编码主要是对解空间进行映射，因此具体选择二进制编码还是十进制编码的关键是根据具体问题进行分析。例如，在对复杂函数寻找最优解时，使用二进制更容易进行对应。而在进行带时间窗的车辆路径规划时，采用十进制编码更合适。所以，基于群体竞争的遗传算法在编码方式上并没有改变。

1.2 选择方式

选择方式的不同对遗传算法具有很大影响，因为选择的目的是要留下强势的个体，但怎样留、留多少将会关系到算法的运算时间及寻优的结果。遗传算法在最早被提出时，使用轮盘赌注法进行选择。跟赌场的轮盘赌注有很大的相似性，某个个体是否被留下具有一定的随机性。

后来有人使用了精英保留算法，即每次进行选择时都对所有个体的适应度函数进行排序，保留适应度函数最高的1～3个个体。

基于群体竞争的遗传算法，结合了轮盘赌注与精英保留策略的双重优势，将群体中的任意两个个体进行适应度对比，保留适应度高的一个个体。这样既存在随机性，又能将优势个体尽量保存下来，从而既保证寻优效率，又保证全局寻优能力。

1.3 交叉逻辑

传统的遗传算法是将新产生的种群中所有个体按一定概率来交叉任意两个个体中的某段基因，从而增大了出现优秀基因的可能性。在群体竞争遗传算法中，只对新产生的个体基因组进行改变。也就是说，将最优的5个个体进行记忆，从这5个个体中随机抽取一段基因注入新产生的个体，然后随机产生新个体的其他位置基因。这样既容易将优秀基因留取，又容易产生新的个体，从而避免寻优过程陷入局部最优。

1.4 变异规则

变异是以一定的概率改变某个个体上的某个基因。变异的概率不能过大，因为这样会降低检索效率。但是，变异也不能完全存在，否则可能会导致检索过程陷入局部最优而无法自拔。所以，适当的变异概率对寻优过程是有益的。

2 群体竞争遗传算法在复合函数寻优上的优势

为了对比普通遗传算法和基于群体竞争遗传算法在寻优能力上的不同，本研究对一个复合函数进行寻优求解。设函数为：

[f（x）=（x-3）2+10sin5x+7cos4x+3sin（2x-1）]       （1）

下面分別用两种算法求解此函数的最优极大值。

2.1 普通遗传算法

2.1.1 求解过程。若采用普通遗传算法，则求解过程如下：

clear all;

close all;

clc;

Population_size=50;                         %种群数

L=20;                                       %二进制编码长度

P_cross=0.8;                                %交叉概率

P_mutates=0.2;                              %变异概率

Generation=100;                             %遗传代数

X_max=10;                                   %自变量最大值

X_min=0;                                    %自变量最小值

g=randint（Population_size，L）;          %随机产生种群

% 遗传算法循环

for j=1：Generation

for i=1：Population_size                 %算适应度值

M=g（i，：）;

m=0;

for k=1：L

m=M（k）*2^（k-1）+m;

end

x（i）=X_min+m*（X_max-X_min）/（2^L-1）;

Fitness（i）=func1（x（i））;

end

maxFitness=max（Fitness）;

minFitness=min（Fitness）;

r=find（Fitness==maxFitness）;%寻找种群中的最优值

g_Best=g（r（1，1），：）;

x_Best=x（r（1，1））;

Fitness=（Fitness-minFitness）/（maxFitness-minFitness）;

% 基于轮盘赌的复制操作

sum_Fitness=sum（Fitness）;

fitvalue=Fitness./sum_Fitness;

fitvalue=cumsum（fitvalue）;

ms=sort（rand（Population_size，1））;

fiti=1;

newi=1;

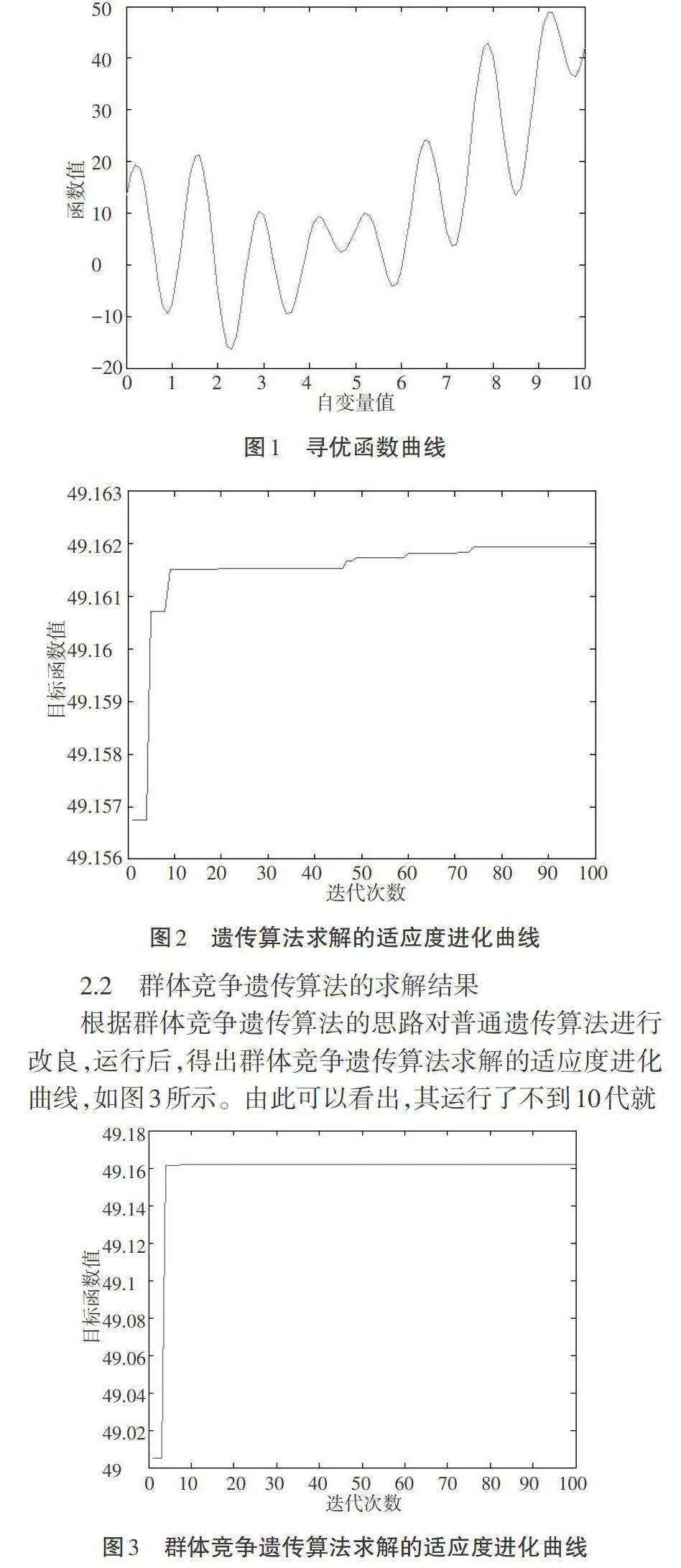
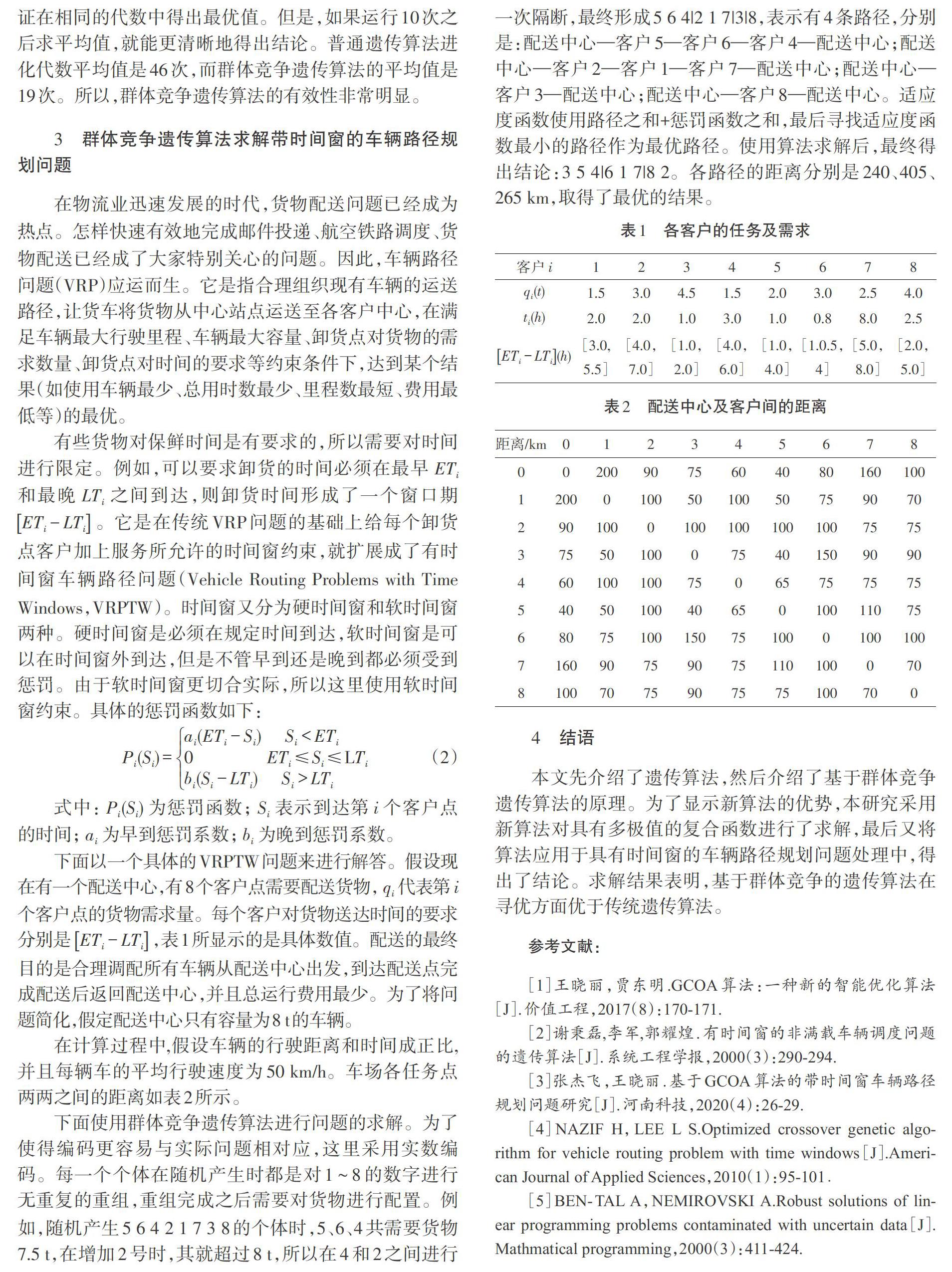
while newi<=Population_size

if （ms（newi））

n_f（newi，：）=g（fiti，：）;

newi=newi+1;

else

fiti=fiti+1;

end

end

% 基于概率的交叉操作

for i=1：2：Population_size

P=rand;

if P

q=randint（1，L）;

for k=1：L

if q（k）==1;

temp=n_f（i+1，k）;

n_f（i+1，k）=n_f（i，k）;

n_f（i，k）=temp;

end

end

end

end

% 基于概率的变异操作

i=1;

while i<=round（Population_size*P_mutates）

h=randint（1，1，[1，Population_size]）;

for k=1：round（L*P_mutates）

gg=randint（1，1，[1，L]）;

n_f（h，gg）=～n_f（h，gg）;

end

i=i+1;

end

g=n_f;

g（1，：）=g_Best;

trace（j）=maxFitness;

end

% 显示找出的最大值及自变量位置

m=0;

for k=1：L

m=g_Best（k）*2^（k-1）+m;

end

x=X_min+m*（X_max-X_min）/（2^L-1）

maxFitness

t=0：0.1：10;

figure（1）                               %输出适应度进化曲线

plot（trace）

xlabel（'迭代次数'）

ylabel（'目标函数值'）

title（'适应度进化曲线'）

figure（2）              %输出需要寻优的函数曲线

plot（t，func1（t））

xlabel（'自变量值'）

ylabel（'函数值'）

title（'尋优函数曲线'）

% 适应度函数

function result=func1（x）

fit=（x-3）.^2+10*sin（5*x）+7*cos（4*x）+3*sin（2*x-1）;

result=fit;

end

2.1.2 普通遗传算法的求解结果。图1是本研究需要寻优的复合函数，将函数做成具有多个极大值是为了考察算法是否能够跳出局部最优而寻找到全局最优值。算法最终运行70多代之后，找到了最大值49.162。这说明，即使是传统的遗传算法，在进行复核函数寻优时也是没有问题的。遗传算法求解的适应度进化曲线见图2。

2.2 群体竞争遗传算法的求解结果

根据群体竞争遗传算法的思路对普通遗传算法进行改良，运行后，得出群体竞争遗传算法求解的适应度进化曲线，如图3所示。由此可以看出，其运行了不到10代就

得出了最优解。无论是哪种遗传算法，并不能每次都保证在相同的代数中得出最优值。但是，如果运行10次之后求平均值，就能更清晰地得出结论。普通遗传算法进化代数平均值是46次，而群体竞争遗传算法的平均值是19次。所以，群体竞争遗传算法的有效性非常明显。

3 群体竞争遗传算法求解带时间窗的车辆路径规划问题

在物流业迅速发展的时代，货物配送问题已经成为热点。怎样快速有效地完成邮件投递、航空铁路调度、货物配送已经成了大家特别关心的问题。因此，车辆路径问题（VRP）应运而生。它是指合理组织现有车辆的运送路径，让货车将货物从中心站点运送至各客户中心，在满足车辆最大行驶里程、车辆最大容量、卸货点对货物的需求数量、卸货点对时间的要求等约束条件下，达到某个结果（如使用车辆最少、总用时数最少、里程数最短、费用最低等）的最优。

有些货物对保鲜时间是有要求的，所以需要对时间进行限定。例如，可以要求卸货的时间必须在最早[ETi]和最晚[LTi]之间到达，则卸货时间形成了一个窗口期[ETi-LTi]。它是在传统VRP问题的基础上给每个卸货点客户加上服务所允许的时间窗约束，就扩展成了有时间窗车辆路径问题（Vehicle Routing Problems with Time Windows，VRPTW）。时间窗又分为硬时间窗和软时间窗两种。硬时间窗是必须在规定时间到达，软时间窗是可以在时间窗外到达，但是不管早到还是晚到都必须受到惩罚。由于软时间窗更切合实际，所以这里使用软时间窗约束。具体的惩罚函数如下：

[Pi（Si）=ai（ETi-Si）SiLTi]             （2）

式中：[Pi（Si）]为惩罚函数;[Si]表示到达第[i]个客户点的时间;[ai]为早到惩罚系数;[bi]为晚到惩罚系数。

下面以一个具体的VRPTW问题来进行解答。假设现在有一个配送中心，有8个客户点需要配送货物，[qi]代表第[i]个客户点的货物需求量。每个客户对货物送达时间的要求分别是[ETi-LTi]，表1所显示的是具体数值。配送的最终目的是合理调配所有车辆从配送中心出发，到达配送点完成配送后返回配送中心，并且总运行费用最少。为了将问题简化，假定配送中心只有容量为8 t的车辆。

在计算过程中，假设车辆的行驶距离和时间成正比，并且每辆车的平均行驶速度为50 km/h。车场各任务点两两之间的距离如表2所示。

下面使用群体竞争遗传算法进行问题的求解。为了使得编码更容易与实际问题相对应，这里采用实数编码。每一个个体在随机产生时都是对1～8的数字进行无重复的重组，重组完成之后需要对货物进行配置。例如，随机产生5 6 4 2 1 7 3 8的个体时，5、6、4共需要货物7.5 t，在增加2号时，其就超过8 t，所以在4和2之间进行一次隔断，最终形成5 6 4|2 1 7|3|8，表示有4条路径，分别是：配送中心—客户5—客户6—客户4—配送中心;配送中心—客户2—客户1—客户7—配送中心;配送中心—客户3—配送中心;配送中心—客户8—配送中心。适应度函数使用路径之和+惩罚函数之和，最后寻找适应度函数最小的路径作为最优路径。使用算法求解后，最终得出结论：3 5 4|6 1 7|8 2。各路径的距离分别是240、405、265 km，取得了最优的结果。

4 结语

本文先介绍了遗传算法，然后介绍了基于群體竞争遗传算法的原理。为了显示新算法的优势，本研究采用新算法对具有多极值的复合函数进行了求解，最后又将算法应用于具有时间窗的车辆路径规划问题处理中，得出了结论。求解结果表明，基于群体竞争的遗传算法在寻优方面优于传统遗传算法。

参考文献：

[1]王晓丽，贾东明.GCOA算法：一种新的智能优化算法[J].价值工程，2017（8）：170-171.

[2]谢秉磊，李军，郭耀煌.有时间窗的非满载车辆调度问题的遗传算法[J].系统工程学报，2000（3）：290-294.

[3]张杰飞，王晓丽.基于GCOA算法的带时间窗车辆路径规划问题研究[J].河南科技，2020（4）：26-29.

[4]NAZIF H，LEE L S.Optimized crossover genetic algorithm for vehicle routing problem with time windows[J].American Journal of Applied Sciences，2010（1）：95-101.

[5]BEN-TAL A，NEMIROVSKI A.Robust solutions of linear programming problems contaminated with uncertain data[J].Mathmatical programming，2000（3）：411-424.