基于稀疏逻辑回归的链接模型在分类问题的应用

摘  要：随着科技的发展，数据分类问题应用在生活的多个方面，然而在面对庞大的数据时，往往采用压缩过的稀疏数据，这就为分类模型的发展带来了极大的挑战。为了提高稀疏数据分类的准确性和正确率，提出了基于稀疏逻辑回归的链接神经网络模型，由此构建成可靠的分类模型。以两类数据作为研究对象，首先进行数据预处理，再提取出数据特征对其进行分类。研究结果表明，分类模型不仅可以应用于稀疏数据，而且正确率较神经网络模型的结果有所提升，手写字的正确率从90.1%提高到94.86%，声音分类的正确率从70.3%提高到74.4%，证实该模型有效。

关键词：逻辑回归;稀疏性;神经网络;多分类

中图分类号：TP391     文献标识码：A

Abstract： With the development of science and technology， data classification is applied in many aspects of life. However， when facing huge data， compressed sparse data is often used， which brings great challenges to the development of classification models. In order to improve the precision and accuracy of sparse data classification， this paper proposes a link neural network model based on sparse logistic regression， so to build a reliable classification model. Taking two types of data as research object， data is preprocessed first， and then data features are extracted to classify them. The research results show that the classification model proposed in this paper can not only be applied to sparse data， but the accuracy is improved compared with the results of the neural network model. Accuracy of handwriting has increased from 90.1% to 94.86%， and accuracy of sound classification has increased from 70.3% to 74.4%， which proves that the model is effective.

Keywords： logistic regression; sparsity; neural network; multi-classification

1   引言（Introduction）

在現代数据分析中，具有挑战性的热点问题是从看似不足的数据量中恢复高维的信号，即数据的稀疏表示，这类问题在多个领域都有所涉及，例如压缩感知、稀疏近似和低秩矩阵恢复。本文受文献[1]1-Bit压缩感知中逻辑回归模型的收敛性以及可行性证明的启发，利用逻辑回归模型并结合稀疏性对实际应用问题进行研究。逻辑回归是最基本的回归形式，也是常用的分类方法。

现代生活的各个方面都离不开“分类”这一概念，应用逻辑回归模型解决分类问题备受研究者的关注，应用于图片分类[2]、医学诊断[3]等多个领域。本文对手写字和海洋哺乳动物数据集进行分类，海洋哺乳动物选取大西洋点斑原海豚、弓头鲸等10类作为研究对象，通过神经网络对分类数据集进行训练之后的训练集再进行逻辑回归模型训练的多分类实验，从而提高正确率。

2   逻辑回归模型（Logistic regression model）

2.1   基本逻辑回归模型

回归问题通常被分为两种形式：线性回归和逻辑回归[4-5]。在统计学方面，线性回归通常用于预测分析。它在数学模型上决定了一个或多个自变量与一个因变量之间在线性关系中的程度。第二种类型的回归分析是逻辑回归[6]，这也是本文要关注和进行分析的。逻辑回归虽然命名为回归，但实际上是一种线性模型的分类器。在这个模型中，描述单个试验可能结果的概率是用一个逻辑函数来建模的，用来计算或预测二进制事件是否发生的概率。作为一个最优化问题，弹性网正则化是和的组合，并最小化以下代价函数：

3   实验（Experiment）

本文运用上文中基于稀疏性的逻辑回归模型进行手写字和海洋哺乳动物的分类，但是分类结果并没有预想的结果好，还有待提高。故由此引入了神经网络的概念，将神经网络训练后的数据与稀疏性逻辑回归模型相链接，经过实验证实，正确率有了大大提高。

3.1   神经网络

神经网络是目前在国内外很受欢迎的机器学习技术[8]，也是深度学习的基础，主要包括输入层、输出层和隐藏层。输入层和输出层中的神经元个数固定不变，隐藏层可以根据需要作出调整。本文选用的模型包含两层隐藏层，为四层神经网络，与两层神经网络相比参数较多，也意味着有较强的模拟能力。神经网络的本质目的就是建模特征与目标之间的函数关系，当参数变多时，模拟出的函数会更加复杂，也会有足够的容量去拟合特征与目标之间真正的关系。

各层神经元之间相连接，每一个连接上都设置权重，若想将神经网络的训练算法达到最优值，通过调整权重的值即可，从而使预测结果达到最精准。在已知输入和参数、时，就会通过下列各式得出输出值：

其中为激活函数，经常会被用到的激活函数包括Sgn函数、Sigmoid函数、Relu函数。本文中将使用Relu函数，其为分段线性函数，与其他函数相比具有较好的收敛性，从而使预测结果更好。其表达式为，当≤时，;当时，。

3.2   基于稀疏性的逻辑回归链接神经网络模型

本文以手写字和海洋哺乳动物分类为例，手写字的总样本中训练集有12，500 个数据，测试集有2，000 个数据;海洋哺乳动物声音的总样本中训练集有700余个数据，其中每种海洋哺乳动物声音各50 个左右;测试集有190 個数据。本文的数据集取材于Kesci中的相关数据，截取了10类海洋哺乳动物声音对比度、色度和音频特征等特征的数据值，再对这些数据通过编号、降维、拟合和转换等过程整理成我们需要的数据，并将类别向量转换成二进制矩阵类型，为后续的分类训练做准备。

首先利用Keras搭建包含两层隐藏层的四层神经网络来解决多分类问题，读取训练之后的数据，将其转化为稀疏矩阵。此时要注意的是，通过Dropout函数得到稀疏数据时，需要把读取到的数据复制100 遍，才能保证分类时数据被正确训练。得到稀疏矩阵之后再通过逻辑回归分类器进行训练，从而得到我们希望的分类结果。本文的核心实验代码如表1所示。

3.3   分类结果

本实验比较了只进行神经网络训练和神经网络与逻辑回归相链接分类时的正确率和模型损失，手写字的正确率从90.1%提高到94.86%，海洋哺乳动物分类的正确率从70.3%提高到74.4%。可以看出，进行两次分类训练的结果是较好的，经过后续实验也可以反映出数据集的数据量越大，正确率提高得越明显。我们用一张对比图可以清晰地看出在添加逻辑回归模型之前与添加之后正确率的变化，如图1所示。

以下展示了应用两种模型对手写字进行分类的正确率结果，如图2和图3所示。

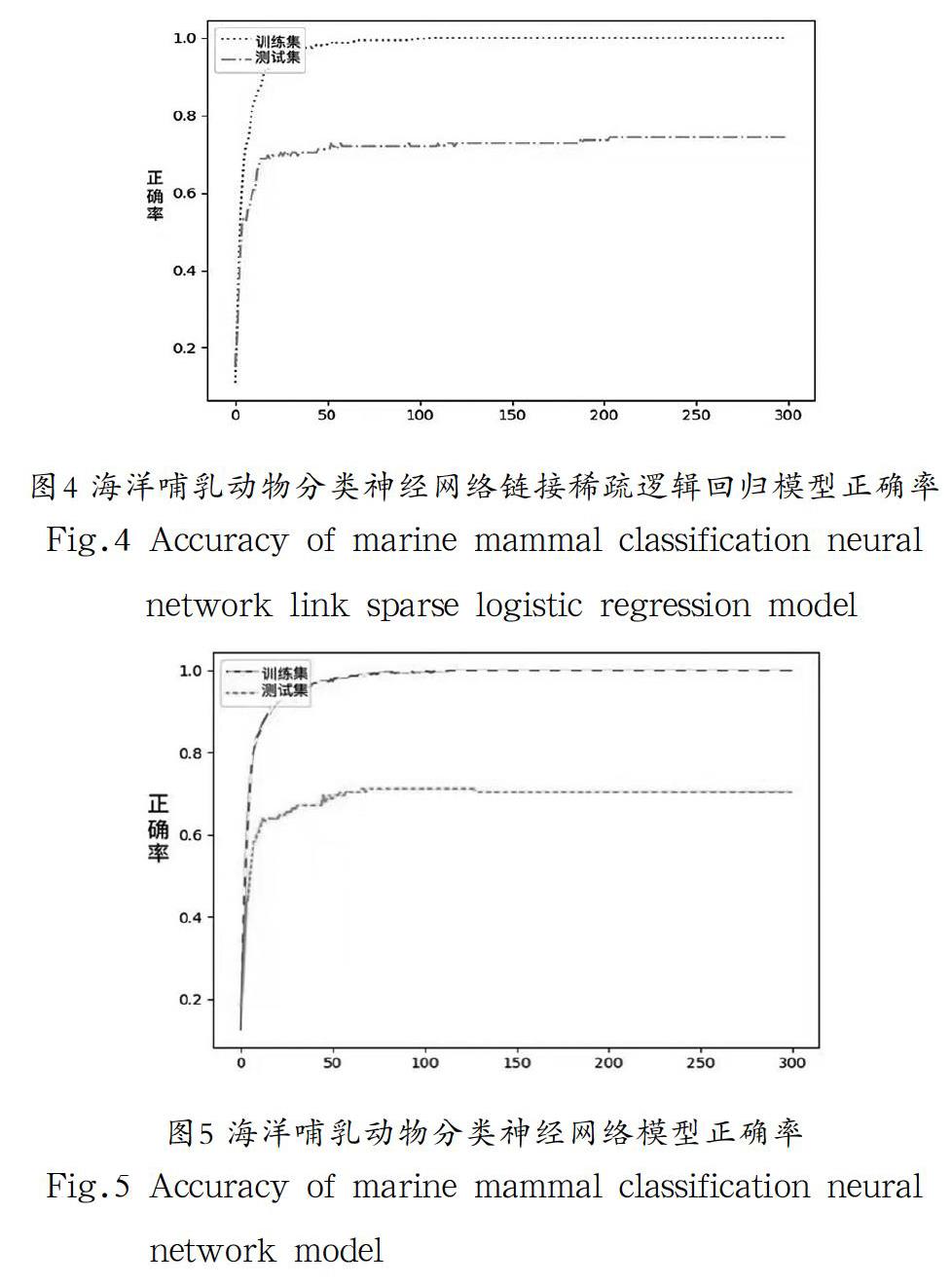
以下展示了应用两种模型对海洋哺乳动物进行分类的正确率结果，如图4和图5所示。

4   结论（Conclusion）

本文主要探讨了逻辑回归模型，并利用这一模型结合稀疏性进行分析。核心内容稀疏性逻辑回归模型经过本文中的实验证实，嵌入神经网络可以明显提高正确率，因而在今后的分类问题当中也可以有效被运用。在今后的研究中，可以加强稀疏性在程序运行方面的设置，并且运用多种方法与神经网络模型相链接并进行比较，选取正确率较高的链接模型。

参考文献（References）

[1] PLAN Y， VERSHYNIN R. Robust 1-bit compressed sensing and sparse logistic regression： A convex programming approach[J]. IEEE Transactions on Information Theory， 2012（7）：13-15.

[2] CAO F X， YANG Z J， REN J C， et al. Extreme sparse multinomial logistic regression： A fast and robust framework for hyperspectral image classification[J]. Remote Sensing， 2017， 9（12）：1255-1269.

[3] 刘蕾.基于逻辑回归算法的乳腺癌诊断数据分类研究[J].软件工程，2018，21（2）：21-23.

[4] FAN J， HECKMAN N. Local polynomial kernel regression for generalized linear models and quasi-likelihood functions[J]. Journal of the American Statistics Association， 1995， 90（429）：141-150.

[5] 王正存，肖中俊，严志国.逻辑回归分类识别优化研究[J].齐鲁工业大学学报，2019，33（5）：47-52.

[6] 王鹏.面向不平衡数据分类问题的核逻辑回归算法的设计与实现[D].西安：西安电子科技大学，2015.

[7] CAI T， XU G. Shifting inequality and recovery of sparse signals[J]. IEEE Transactions on Signal Processing， 2010， 58（3）：1300-1308.

[8] 邢珍珍.卷积神经网络在图像处理中的应用研究[J].软件工程，2019，22（6）：5-7.

作者简介：

常鈺迪（1996-），女，硕士生.研究领域：压缩感知，稀疏恢复.