基于迭代SVD的电影推荐算法的研究

武文硕 左安

摘要：现有的电影推荐算法中，协同过滤算法是最常使用、操作最简单方便的算法，但传统的协同过滤算法存在评分矩阵稀疏、推荐精度低等问题。针对这些问题，提出了矩阵填充策略，根据矩阵填充技术的优缺点，选择了几种填充稀疏矩阵的方法，并且利用迭代SVD算法得到了电影推荐的局部最优解，并利用均方根误差（RMSE）对结果进行了评价，利用R软件对电影评分数据集进行处理，实验结果表明，与传统的协同过滤推荐算法相比，迭代SVD算法能有效地提高推荐的准确性，更加准确地给用户提供想看的电影。

关键词：协同过滤;矩阵填充;稀疏矩阵;电影推荐

中图分类号：TP391.3        文献标识码：A

文章编号：1009-3044（2021）15-0001-03

Abstract： Among the existing film recommendation algorithms， collaborative filtering algorithm is the most commonly used and easy to operate algorithm， but the traditional collaborative filtering algorithm has the problems of sparse rating matrix and low recommendation accuracy. According to the advantages and disadvantages of matrix filling technology， several methods of filling sparse matrix are selected. The local optimal solution of movie recommendation is obtained by using iterative SVD algorithm， and the results are evaluated by root mean square error （RMSE）. Finally， R software is used to process the movie rating data set. The experimental results show that the proposed method is more effective than the traditional method Compared with the collaborative filtering recommendation algorithm based on SVD， the iterative SVD algorithm can effectively improve the accuracy of recommendation and provide users with more accurate movies they want to see.

Keywords： collaborative filtering; matrix filling; sparse matrix; movie recommendation

1引言

随着互联网科技的迅速发展，我们现在进入信息时代，信息量呈现爆炸式地增长，人们从网上搜到的数据越来越多，相比之下，有用的数据量少之又少。为了帮助人们从纷繁复杂的信息中，找到自己需要的内容，个性化推荐系统应运而生，本文介绍了电影推荐算法以及改进算法，通过对大量的数据进行处理分析、数据可视化，得出结论是通过SVD处理后，推荐精度能够得到进一步的提升，有效克服了传统推荐算法的缺点。

2研究方法

2.1协同过滤算法

协同过滤算法是一种较为著名和常用的推荐算法，它是通过用户的历史搜索记录和浏览记录等信息，对这些信息进行数据挖掘，与相似的客户群体和物品进行对比，发现客户的喜好，据此预测用户可能喜好的产品进行推荐。也就是常见的“猜你喜欢”，和“购买了该商品的人也喜欢”等功能。它的主要实现由：

1） 根据和你有共同喜好的人给你推荐;

2） 根据你喜欢的物品给你推荐相似物品;

3） 根据以上条件综合推薦。

因此可以得出常用的协同过滤算法分为两种，基于用户的协同过滤算法，以及基于项目的协同过滤算法。特点可以概括为“物以类聚，人以群分”，并据此进行预测和推荐。本文将使用基于用户的协同过滤算法（UBCF） 、基于项目的协同过滤算法（IBCF） 、基于SVD的协同过滤算法，这三种基础的协同过滤算法作为参照组进行比较。协同过滤推荐算法的基本原理是通过“用户-项目“评分矩阵Z计算相似度，评分矩阵Z为m×n维矩阵，m为用户的数目，n为项目的数目，每一个元素[ru，i]表示用户u对项目i的评分。该评分矩阵一般是具有强“稀疏性”（sparsity）的大矩阵。图1空白位置对应矩阵的数据缺失。

传统的协同过滤推荐算法通常有以下三个缺点：稀疏性，从上图我们可以看出来空白的地方非常大，表明数据矩阵非常稀疏，形成目标用户的最近用户集时，往往会造成信息缺失，从而导致推荐效果降低;冷启动性，冷启动又叫作第一评价问题，或新物品问题，当新项目和新用户首次出现的时候，评价和反馈的信息都比较少，使得推荐的效果差强人意，一定程度上看成是稀疏矩阵的极端情况;最后就是可扩展性，面对每日新增的用户和增多的电影数量，数据量急剧增长，算法面对不断扩大的数据规模，推荐准确性下降，即可扩展性面临挑战。

针对以上推荐算法的不足之处，本文提出迭代奇异值分解（Singular Value Decomposition，SVD）来解决这些问题。

2.2迭代SVD算法

具体来说，对于[Z：m×n]， 令[Ω?{1，…，m}×{1，…，n}]表示[Z]中观测到的元素的索引的集合，给定这些观测值，一个自然的思路是可对应寻找[Z]的最低秩矩阵[Z]，即[Z=argminM∈Rm×nrank（M），其约束为mij=zij，（i，j）∈Ω]。

但含缺失数据的最低秩问题计算非常困难，一般无法求解。因此，更常见的求解方法是允许所得到的[M]矩阵与观测值之间有一定误差，即

[Zr=argminrank（M）≤r（i，j）∈Ω（zij-mij）2]

该问题是非凸优化，通常得不到最优解，但可以采用迭代算法来得到局部最优解。

步骤一：通过对[Z]进行随机填充，初始化[Z];

步骤二：通过计算[Z]的r秩SVD求解[M]：

[Z=UDVT， M←UrDVT;]

步骤三：基于[M]对[Z]的缺失部分进行填充：

[zij←mij，（i，j）?Ω;]

步骤四：重复第2-3步，直至算法收敛。

2.3预测准确度

预测准确度是用来评价电影推荐算法的预测评分与用户的实际评分是否接近的指标，在推荐系统中，预测准确度是很重要的参数，通过准确度的计算，我们可以知道推荐算法的有效程度。常用的预测评分准确度标准有：平均绝对误差（MAE） 、均方根误差（RMSE） ，定义如下：

[MAE=i=1N|ri-ri|N]                            （1）

[RMSE=i=1N（ri-ri）^2N]                           （2）

其中[ri]表示的是用户u对于项目i的真实评分，[ri]表示的是预测评分，N表示测试集的大小。从公式可以看出RMSE更复杂且偏向更高的误差，而且用RMSE来定义损失函数是平滑可微的，因此它是许多模型的默认度量标准。我们本文选择RMSE作为分析结果的标准，为了说明样本的离散程度，RMSE的数值越小代表准确度越高。

3实验分析

3.1实验数据集

针对此次电影推荐算法的研究，选用的数据集是Movielens电影评分数据集中最小的一组数据MovieLenslastest small是最小的一组数据，此数据集是由美國明尼苏达大学Grouplens项目从Movielens站点整理而来，广泛应用于个性化推荐算法研究中，数据集包括600余名用户对9000余部电影1，000，000余个评分（1～5），评分值越高表示越满意。原始数据可从grouplens.org/datasets/movielens下载， 根据包含的数据量与评分年份的不同， 提供了不同的版本。

3.2实验设计和结果分析

第一步利用R语言自带的Recommender包对Movielenslastest small数据集进行处理，得到RMSE的值，这是传统协同过滤算法得到的结果，作为标准组进行对照，结果如下表1：

从结果我们可以看出，svd算法的RMSE值最小，在基于用户，基于项目和基于svd的协同算法中，基于svd的方法更加有效一点，具有更好的推荐效果。

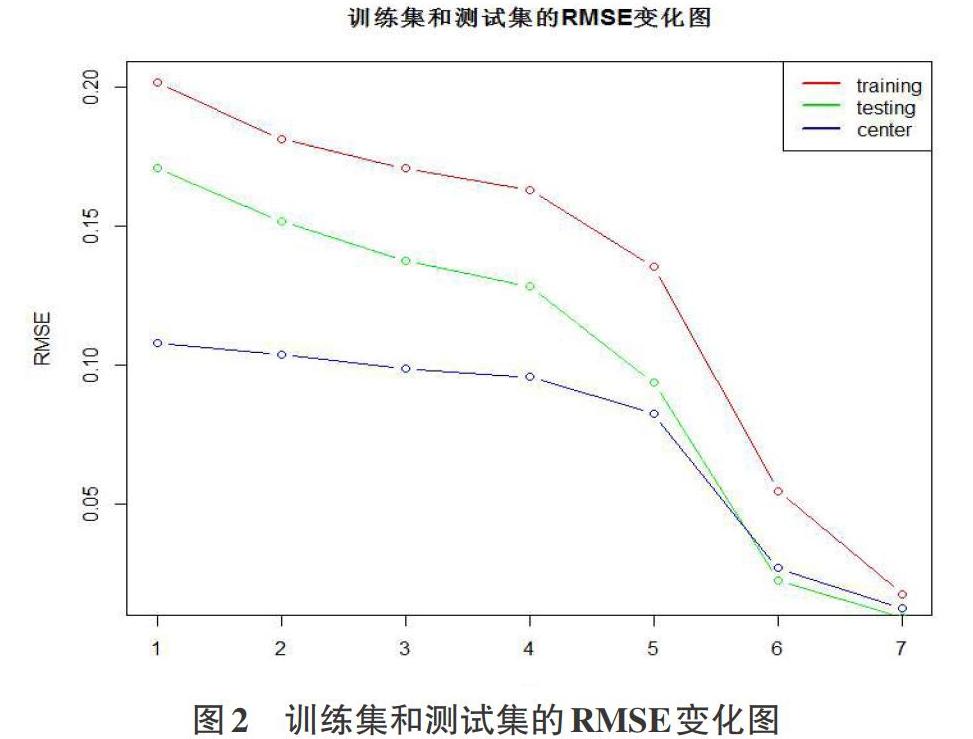
第二步对传统协同算法进行改进，将数据集随机抽取75%左右的评分为训练集，25%为测试集，利用上述迭代SVD算法，在Movielens数据集上进行评分填充，选取秩r为2，3，4，5，10，50，100， 分别报告评分填充在训练集和测试集上的RMSE， 对训练集的数据矩阵行和列进行中心化，对中心化后的训练集数据矩阵也求解RMSE，得到的结果如下表2所示：

实验数据表明，随着秩r逐渐增大，RMSE逐渐减小，这表明当r越大，推荐精度越准确，训练集和测试集的数据量不同;从图中可以清晰地看出，测试集的RMSE明显小于训练集，说明数据量的大小会影响推荐算法的精确度，并不是数据越多评分准确率就会高，而是数据量少一点，推荐就会越准确因此在实际过程中可以适当减少数据量，这也会相应减少建立模型所用的时间;其次就是对训练集数据矩阵行和列进行中心化后，能够明显提高推荐算法的准确性，随着秩r的增加，中心化前后的数据矩阵推荐精度相差不大。由以上可知此算法的推荐效果较为有效。

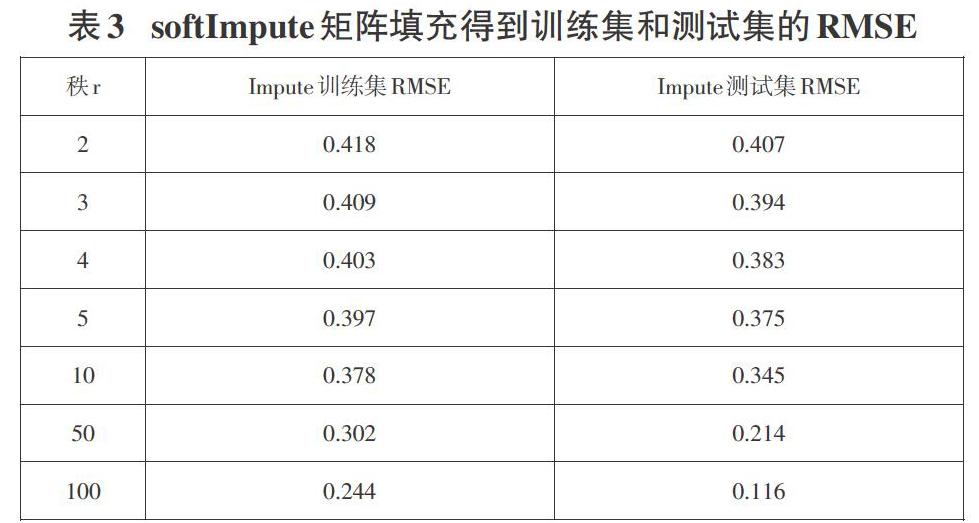
第三步是利用R包softImpute对训练集和测试集进行矩阵填充时得到的RMSE如表3所示：

从这种数据填充方法的结果来看，RMSE的值要比传统推荐方法的小一点，但是和第二步得到的结果相比大得多，所以使用R语言自带的包对矩阵进行填充能够解决矩阵稀疏性的问题，提高推荐的准确性，但是相比之下还是本文提出的迭代SVD算法优化效果更加显著。

4论文总结

本文介绍了几个不同的电影推荐算法，主要是基于矩阵填充的迭代SVD协同过滤算法，通过对数据矩阵采用不同的填充方式，解决了数据的稀疏性问题，然后比较均方根误差（RMSE）的结果。实验结果表明，对数据矩阵进行矩阵填充之后能够提高评分的准确度，其中对信息矩阵的行和列进行中心化最为准确。然而，我们判断的方法也有一定的局限性，首先评判标准过于单一，数据的可信度可能不够，此外影响推荐算法准确度的因素还有很多，比如虚假评分和用户兴趣随时间改变的影响，会对我们的实验结果有不利的影响。

在实验过程中也遇到了一些问题，由于填充的数据量有些大，给内存和运算带来了一定的挑战，在进行迭代循环所耗费的时间也是比较长的，这也是下一步需要解决的问题。

参考文献：

[1] 徐吉.基于协同过滤和矩阵分解的推荐系统研究与应用[D].宁波：宁波大学，2019.

[2] 吴涛.推荐系统中推荐算法研究及其应用[D].北京：北京交通大学，2019.

[3] Mazumder R，Hastie T，Tibshirani R.Spectral regularization algorithms for learning large incomplete matrices[J].Journal of Machine Learning Research，2010，11：2287-2322.

[4] Sarwar B，Karypis G，Konstan J，et al.Application of dimensionality reduction in recommender system - A case study[R].Defense Technical Information Center，2000.

[5] 袁泉，成振华，江洋.基于知识图谱和协同过滤的电影推荐算法研究[J].计算机工程与科学，2020，42（4）：714-721.

[6] 王祥德，雷玉霞，闫昱姝.基于矩阵填充的SVD协同过滤算法研究[J].微型机与应用，2017，36（19）：55-57，61.

[7] 吴志鹏.基于矩阵分解的推薦算法研究[D].北京：北京邮电大学，2019.

[8] 彭石，周志彬，王国军.基于评分矩阵预填充的协同过滤算法[J].计算机工程，2013，39（1）：175-178，182.

[9] 马宏伟，张光卫，李鹏.协同过滤推荐算法综述[J].小型微型计算机系统，2009，30（7）：1282-1288.

[10] 韩亚楠，曹菡，刘亮亮.基于评分矩阵填充与用户兴趣的协同过滤推荐算法[J].计算机工程，2016，42（1）：36-40.

[11] 聂常超.一种基于矩阵分解的电影推荐算法[J].电子设计工程，2016，24（19）：73-75.

[12] 郭珈辰.电影推荐算法的研究与实现[D].长春：吉林大学，2015.

[13] 陈垠芬.基于矩阵填充与图嵌入表示的个性化推荐算法研究[D].南昌：江西师范大学，2019.

[14] 赵军，王红，殷方勇.一种面向稀疏和虚假评分的协同推荐方法[J].小型微型计算机系统，2017，38（3）：472-477.

[15] 陈垲冰，黄荣，吴明芬，等.一种基于电影评分预测的协同过滤[J].哈尔滨师范大学自然科学学报，2018，34（6）：1-5，11.

[16] 黄丽.基于SVD的协同过滤推荐算法研究[J].电脑知识与技术，2019，15（21）：9-10.

[17] 张玉叶.基于协同过滤的电影推荐系统的设计与实现[J].电脑知识与技术，2019，15（6）：70-73.

【通联编辑：王力】