基于IMM Kalman滤波算法的实时追踪监控系统

张凯丽 何 玥 程雅茹 孙晨静 陈亚宁 纪亚芳

（山西师范大学物理与信息工程学院，山西 临汾 041000）

1 引言

随着各行各业的飞速发展，国家对人民的人身安全、财产安全的重视不断提高。视频监控已经从最初只在特殊行业中使用，发展为各行各业的必备产品。但是在这种社会背景下，依然有不法分子顶风作案，拐卖儿童、入室抢劫等案例仍然存在。

在寻找走失儿童与抓捕罪犯的过程中，最常用的方法是通过监控视频观察。监控视频中记录了他们犯罪的证据，但是在查看监控回放时，人力监测耗时耗力，容易错过最佳时期，监测过程难免有疏忽遗漏的地方，因此对监控系统的优化是必要的。针对普通监控系统所存在的缺陷，本文采用SAD匹配算法和IMM Kalman滤波算法，对现有的监控系统进行了优化，实现了对监控范围内重点目标全程持续跟踪和信息捕捉，进而完成视频分析。

2 目标检测

目前，对收集到的数据进行前期3D 标定的方法为单目视觉或双目立体视觉。为克服仅使用单目视觉无法对目标精确追踪的缺点，本文采用双目立体视觉方式。双目立体视觉的重点是进行立体匹配，本文通过采用SAD（Sum of Absolute Differences）匹配算法确定左右视图匹配关系，从而实现双目立体视觉目标检测。

SAD匹配算法是将模板图样I（尺寸为m*n）与待检索图样I’（尺寸为M*N）进行对比，寻找出最佳匹配图样。具体算法步骤如下所示：

（1）将待检索图样和模板图样通过卷积神经网络选择出所有像素点；

（2）将模板图样灰度减去待检索图样灰度，求出二者灰度差之和[1]

其中i，j 表示子图的中心坐标，1≤x≤M－m＋1,1≤y≤N－n＋1。

（3）移动模板图样，采用(1)中SAD匹配算法选择出模板图样中的所有像素点，并重复步骤(2)；

（4）当SAD值最小时，则为待检索图样的最佳匹配。

3 目标追踪

目标追踪算法主要是对目标的外观进行追踪，目标外观不被遮挡属于理想情况。在实际检测中，由于受外界因素干扰，目标常会受到遮挡，使追踪出现失效情况，此时可利用IMM Kalman滤波算法修正失效段，对追踪过程进行优化。

3.1 有效性判断

在SAD匹配算法的基础上，采用一种有效性判断方法，其方法的一般步骤如下：

（1）将目标检测时计算的所有SAD值列成矩阵（设模板图样T大小为a*b，待检索图样S大小为A*B），则可知矩阵大小为（A-a+1）*(B-b+1)；

（2）找出SAD最小值在矩阵中的位置坐标（x,y）；

（3）在SAD 矩阵中，以最小值（x,y）为中心点，取一个一定大小的矩阵Gi（矩阵Gi的大小不能太小，否则变化不明显，无法更准确地判断有效性），用Gi来表示某一帧的图像。将矩阵分块，选取不同大小的矩阵，根据选取的矩阵，设置不同大小的权重系数，这就提高了目标跟踪的准确性，减少了目标跟踪过程中受到遮挡等干扰因素的消极影响；

（4）模板图像是从第1帧图像获取的，以第1帧图像对应的G1为依据，与其他帧图像对应的矩阵Gi采用归一化互相关的方法进行计算，公式[1]为：

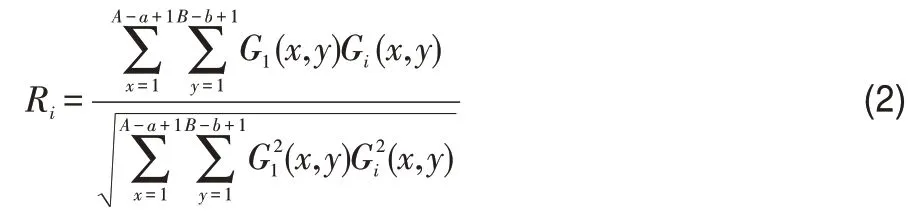
（5）计算模板T的像素平均值[1]：

计算相关性阈值[1]：

将每帧图像对应的Ri与RT进行比较，若Ri≥RT，则相关跟踪有效，否则相关跟踪失效。

3.2 IMM Kalman滤波算法

Kalman 滤波算法是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法[1]。由于观测数据中存在系统噪声和干扰的影响，所以最优估计也可看作是滤波过程。在目标追踪时，可通过Kalman 滤波算法进行动态估计。当目标的运动模型服从高斯分布时，对其运动状态进行预测，将预测模型与观察模型进行对比，根据误差来更新运动目标的状态。由于Kalman 滤波算法一般适用于线性系统，而线性系统属于理想情况，因此在实际应用中存在一些弊端。

本文采用的是IMM Kalman 滤波算法，IMM Kalman 滤波算法是1984年H.A.PBlom基于Kalman滤波算法而提出的一种新型滤波算法。该算法克服了Kalman滤波算法的局限性，通过对多个模型的估计结果进行加权平均，对动态系统进行更优的估计，从而得到更理想的效果。

IMM Kalman滤波算法的一般步骤如下：

（1）设跟踪目标运动状态有m种，与之对应m个运动模型，第j个模型可用如下公式[1]表示：

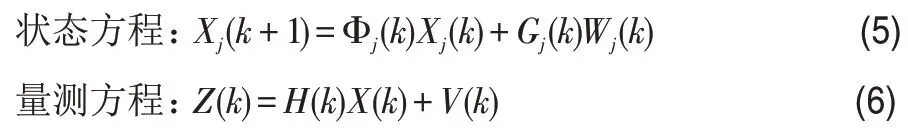
其中Φj(k)是状态转移矩阵，Wj(k)～(0,Qj)是满足高斯分布（均值为0，协方差矩阵为Qj）的白噪声序列，Gj(k)是噪声驱动矩阵，H(k)是系统模型，V(k)是观测噪声。

（2）m种模型间的马尔可夫概率转移矩阵为：

其中pij表示由第i个运动模型转移到第j个运动模型的概率。

（3）由上一步模型概率μj(k-1)得到模型j的预测概率pj，计算出模型i到模型j的混合概率μij(k-1)，结合目标的状态估计得出模型j的混合状态估计，从而得到模型j的混合协方差估计。

模型j的混合状态估计：

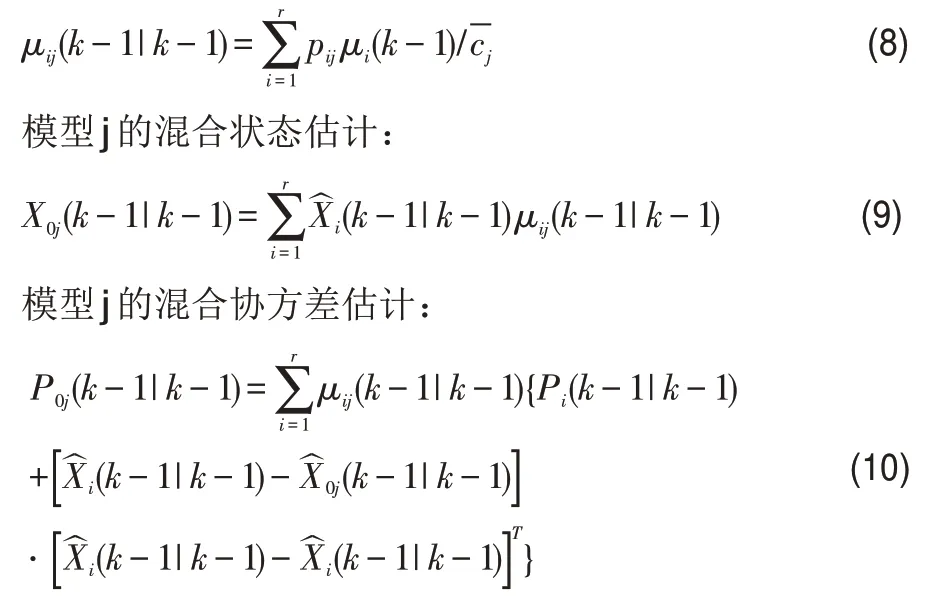
（4）以模型j的混合状态估计、混合协方差估计以及量测方程Z(k)作为输入进行Kalman 滤波，更新预测状态和滤波协方差。

（5）采用似然函数（Likelihood function）对μj(k)进行更新。

模型j的似然函数：

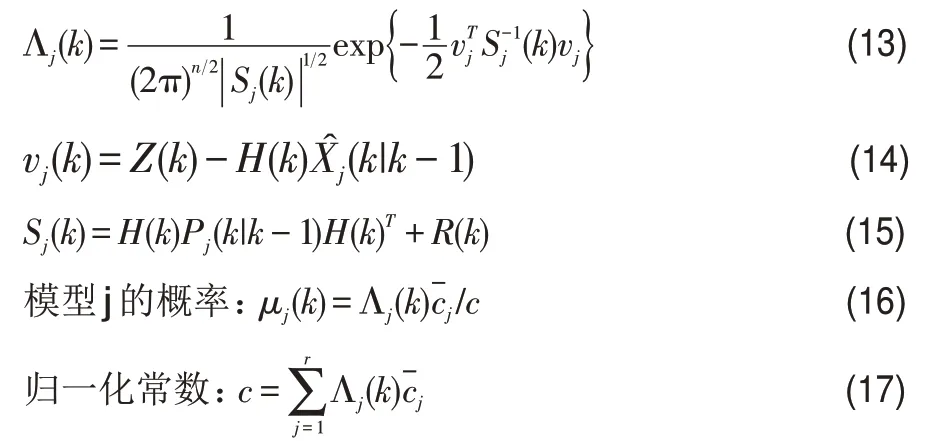
（6）通过对模型j 进行输出交互，计算多个模型估计结果的加权平均值，得到总的状态估计和协方差估计。

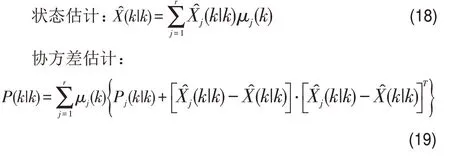
在追踪监控过程中，采用SAD匹配算法和IMM Kalman滤波算法相结合的方式，不断更新目标的概率，从而优化目标追踪的精确度。

4 仿真分析

4.1 SAD匹配算法仿真

用相机平行移动拍摄得到监测目标的左、右两幅视点图像，通过MATLAB对SAD匹配算法进行仿真，结果图1、2所示。

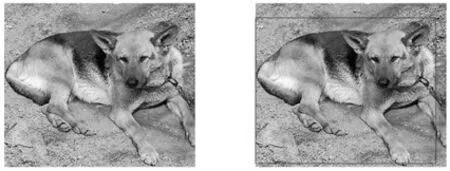
图1 不受遮挡的监测目标

图2 受遮挡的监测目标

如图1、2所示，以左目图像的源匹配点为中心，定义一个窗口，通过移动右目图像逐步计算灰度差值，从而寻找最佳匹配点。仿真得到不同状态下监测目标的检测结果，当目标不受遮挡和受遮挡时，SAD匹配算法都可以无失真地检测出目标。由此可见，SAD匹配算法可实现对目标的检测功能。

4.2 IMM Kalman滤波算法仿真

将目标运动轨迹划分成三个模型：匀速直线运动（模型一），右转（模型二），左转（模型三）。

0～20s，目标向右前方做276m/s 的匀速直线运动；第20s时，改变其运动方向；20s～60s，向左前方做247m/s 的匀速直线运动；第60s时，再次改变目标的运动方向；60s～100s，向右前方做247m/s的匀速直线运动。

图3为目标运动轨迹追踪示意图，由图可知滤波值与目标真实轨迹偏差较小。

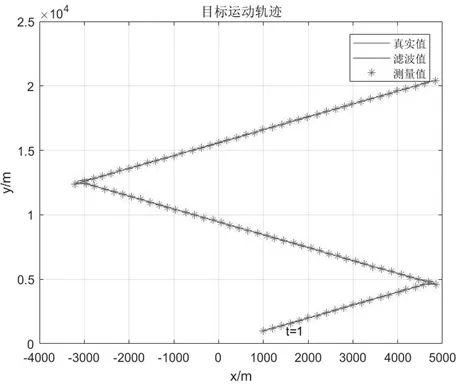
图3 目标运动轨迹

图4和图5分别为追踪过程中目标位置和速度的误差分析曲线。从图中可以看出，目标在做匀速直线运动时，误差值均在0值附近波动，且时间越长误差波动幅度越小，越接近0值；当目标方向突然发生改变时，由于时间较短，变动较大，因此误差值较大；第60s 时相较第20s 时误差值有所下降。分析仿真结果可得，在追踪过程中，随着追踪时间的延长，追踪次数的增加，系统的优化效果会逐渐显著。

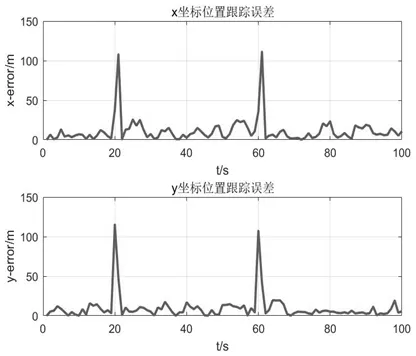
图4 位置跟踪误差

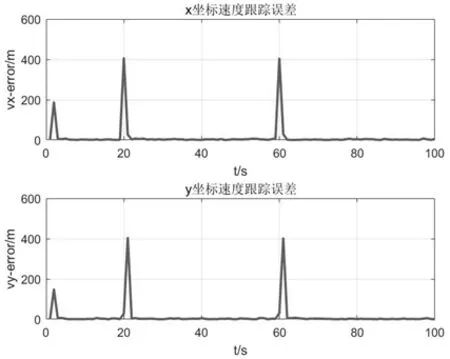
图5 速度跟踪误差

图6 为IMM Kalman 滤波算法模型概率曲线，从图中可以看出，在目标做匀速直线运动的过程中，模型一概率接近100%；在20s时目标左转，模型一概率逐渐降低，模型三概率逐渐提高，最终模型三概率接近100%；60s时刻目标右转，模型一概率逐渐降低，模型二概率逐渐提高，最终模型二概率接近100%。

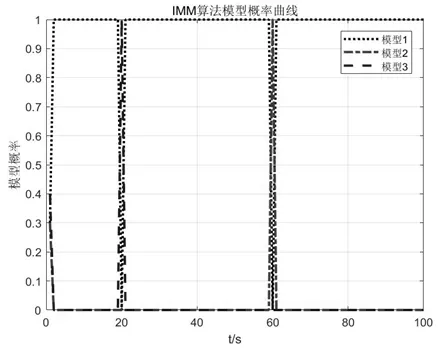
图6 IMM Kalman滤波算法模型概率曲线

5 结论

由仿真结果可知，SAD 匹配算法能确定目标位置，可以用于目标检测。IMM Kalman 滤波算法能修复失效段，可以用于目标追踪。通过仿真软件进行验证，结果表明，在监控设备的辅助下，该系统对监控视频中某目标可以实现检测与追踪功能，具有现实意义。但系统尚未进行实物测试，仍停留在仿真研究阶段，实际测试情况有待进一步研究。