等截面一维声子晶体角梁结构振动特性

张 颖，史冬岩，何东泽

(1.黑龙江八一农垦大学工程学院，大庆 163319；2.哈尔滨工程大学机电工程学院，哈尔滨 150001)

伴随着时代的进步和社会的发展，机械制造业以及加工业对精密仪器的加工越来越重视，尤其对于机械加工制造而言，如何减振降噪已经成为工程机械设计和生产的关键的因素。声子晶体概念是类比于光子晶体的概念而提出的，通过对比与光子晶体，可以明显地比较看出，弹性波传播时，会产生较为特殊的振动带隙。正因为声子晶体结构独特的振动带隙特性，是一个较为新颖的领域，其工程应用价值也存在着较大的潜在价值。目前研究中，对于声子晶体结构振动特性的掌握，仍不足以满足实际应用需求，研究相关结构减振特性具有重要意义。

1 研究现状分析

声子晶体结构存在特殊的周期性结构，当弹性波在其中传播时，会使其在传播过程之中产生较为特殊的色散关系，即能带关系[1]。1883年的Floquet较早对周期材料结构进行讨论，进行了关于一维Mathieus方程的研究。通常将振动衰减范围内的频率定义为带隙，进而提出了声子晶体的概念。近年来，基于光学以及固体物理学研究领域的扩展，光子能带理论和电子能带理论对各类交叉学科领域产生了深远的影响，人们提出了一种新的物理概念——声子晶体，借助于能带理论中的晶格、倒格子、布里渊区以及带隙等相关研究结果，对能带结构以及振动特性进行计算[2]。为了进一步对声子晶体进行研究，需要对声子晶体进行分类，通常可以将声子晶体分为一维、二维以及三维，具体的分类规则是依据周期分布排列的方向数而确定的[3]。在工程实际的应用之中，梁结构较为常用，并且声子晶体梁结构由于其独特性能而具有较为广阔的应用前景；在理论方面，一维声子晶体结构是一种散射体与基体相互不可区分的一维结构，所以其理论模型应具有一定的特殊性，具有重要的研究价值。在工程应用以及装备生产的过程之中，一维声子晶体结构具备稳定机械振动的作用，降低其在生产过程以及对工作环境产生的影响和危害[4]。尤其声辐射、声噪会对用户及操作人员的身心健康产生危害[5]。在国防工业之中，减振更是值得考虑的问题，例如飞机、潜艇、航母等高科技装备的制造和工作中，尤其是在恶劣的环境条件下都需要具有较好的减振特性，明显的振动噪声会造成较多不良后果[6]。

近年来很多学者针对一维声子晶体结构的振动特性开展相关研究。宿星亮等[7]研究了功能梯度材料复合而成的一维声子晶体结构的弹性波带隙特征。左曙光等[8]考察了一维局域共振声子晶体带隙受材料黏弹性的影响。张法[9]采用理论推导、仿真分析及实验验证相结合的研究方法，分析和比较了声子晶体组合杆振动特性。舒海生等[6]针对直梁低维振动特性的不足，提出一类声子晶体角梁结构的理论模型，并开展数值分析，提供该结构减振的有效方法。朱学治等[10]基于欧拉梁理论，分析了有周期分布转动振子的声子晶体梁带隙变化的一般规律。何东泽等[11]将一维声子晶体振动特性的研究拓展到均匀变截面结构当中。涂静等[12]更进一步将振动带隙特性研究拓展到双层欧拉梁声子晶体结构中，指出双层梁结构在减振方面具有特有的优势。

而在以往的研究过程中，大多数的研究主要集中于单一梁的研究，对组合梁的振动特性的研究较少，等截面声子晶体角梁可以视为工程应用上较为常用的梁单元，是一种常见的组合梁。在工程应用之中存在着较多的应用，比如担架的角梁扶手，房屋屋脊框架的结构组成等均是由角梁单元变化而成[11]。基于此，现对一维等截面声子晶体、组合杆件——角梁结构的振动特性进行研究分析，研究各参数对声子晶体角梁振动特性的影响，对发挥其材料和结构优势、有效控制振动和声辐射具有重要意义。

2 角梁模型建立与描述

一维等截面声子晶体角梁结构是由多段等截面一维短粗梁在直角方向上的排列组合而成(图1)，本节主要研究三周期的一维等截面声子晶体角梁，声子晶体角梁的横截面尺寸与轴向尺寸相当。

图1 一维等截面曲梁示意图

选取材料A为有机玻璃，材料B为铝，其性能参数如下：铝：密度为2 799 kg/m3，弹性模量为7.21×1010Pa，泊松比为0.33；有机玻璃：密度为1 442 kg/m3，弹性模量为0.32×1010Pa，泊松比为0.33。

对于一维声子晶体角梁结构，其物理参数如下：材料A的长度为l1=60 mm，材料B的长度为l2=60 mm，则周期常数，即晶格常数N为l1+l2=120 mm；g为组分比，表示结构中两种材料的比例；材料A和材料B的横截面均为矩形，横截面面积相等，即A1=A2，具体参数如下：截面宽度b1=b2=10 mm，高度h1=h2=10 mm。定义角梁的夹角为θ，则本节所研究的角梁夹角θ为90o。

如图2可以表示直角连接处，定义其节点数为2，则可以明确地表示出单元12和单元23中对偶坐标系的建立情况，根据各自坐标系的建立，结合节点处的广义力平衡条件以及广义位移协调条件进行计算，得出整个系统的回传射线矩阵，结合边界条件进行求解，得出相对应的频率相应函数曲线，研究一维等截面声子晶体角梁的振动特性。

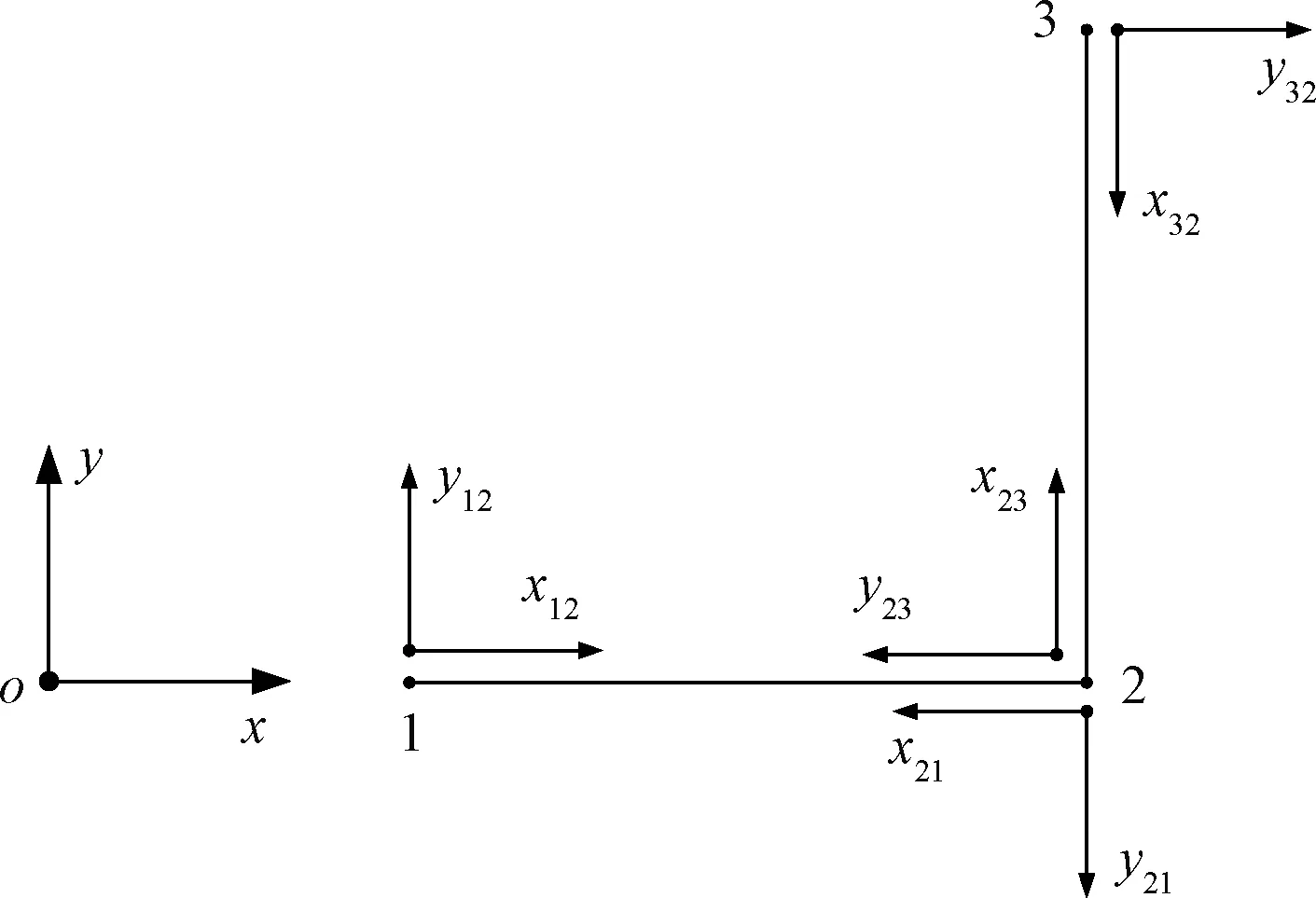
图2 坐标定义

3 回传射线矩阵法

回传射线矩阵法的主要求解思路为：建立整体坐标系，将整个结构划分为若干的单元，建立一对对偶的局部坐标系，根据相应的物理关系得出对应的控制微分方程，进行傅里叶变换，将时域范围内的偏微分方程转化为频域范围内的常微分方程，求出对应的解[13]。将控制微分方程的解写成波的形式，分为入射波和出射波两大类；在同一单元之中，因一端的节点处的出射波，经过在该单元之中的传播过程，在另一单元之中将变为入射波，考虑二者之间的转化关系；将各个单元的相位关系按照节点顺序并且与散射关系中的顺序相同组成总体相位关系矩阵；通过联立总体散射关系矩阵以及总体相位关系矩阵，并且引入转换矩阵，计算得出整体结构的回传射线矩阵，进而求出相应的入射波与出射波的波幅向量，求解对应的物理量[14-16]。

3.1 结构描述

假设一维声子晶体由K段组成，将每一段结构视为一个整体，建立整体坐标系并进行结构定义。则可以将整个声子晶体杆划分为K个整体结构，即，将每一段材料视为一个整体结构，分别建立整体坐标系和对偶坐标系进行求解。通常采用数字对节点以及单元进行编号，如图3所示为对声子晶体杆进行节点分配以及结构定义，其中，K=6。

图3 结构描述示意图

3.2 总体坐标与单元局部坐标

对于一根杆单元，如i、j，分别引入对偶的局部坐标系(x,y,z)ij和(x,y,z)ji，分别以i和j为相应的坐标原点，以单元的轴线方向为x轴方向。对于(x,y,z)ij坐标系而言，以i到j的方向为正方向，相对应的，(x,y,z)ji以j到i的方向为正方向。将xij和xji在xy平面内逆时针旋转90°即可得到yij和yji，根据各自坐标系中x和y的正方向，结合右手螺旋法则，得到对应的zij和zji。对偶坐标的具体形式如图4所示。从图4中可以看出，xij和xji方向相反，yij和yji方向相反，zij和zji方向相同。在对偶坐标系中，坐标x满足关系式:xij=lij-xji以轴向位移u为例，可以得到uij=-uji。

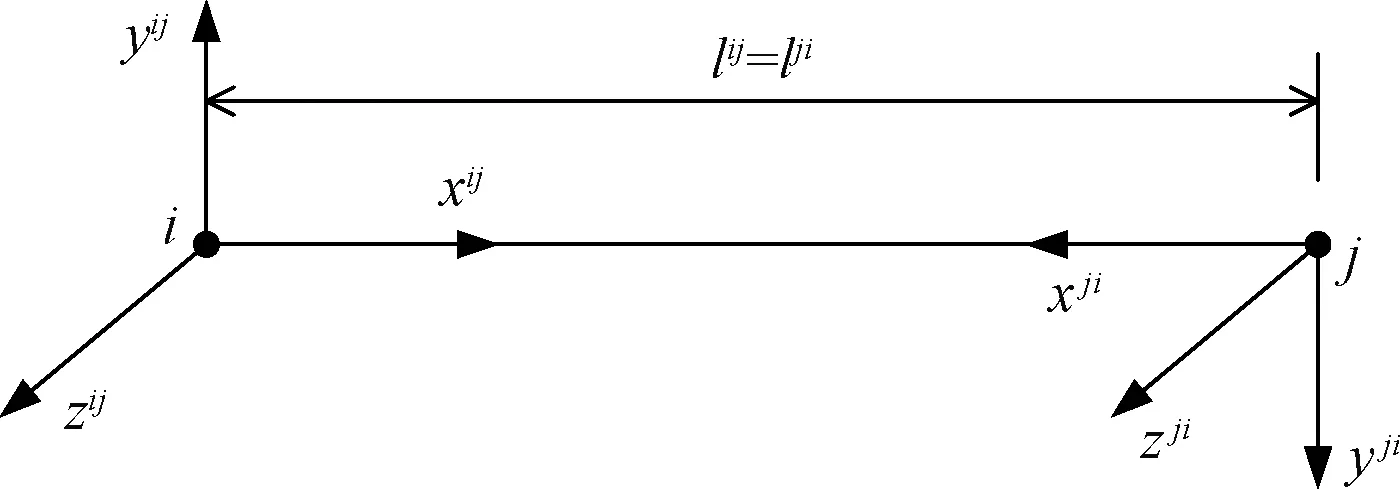
图4 单元的对偶坐标系

3.3 坐标变换与对偶变换

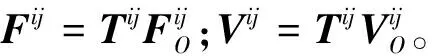
图5 局部坐标系与整体坐标系之间的关系

(1)

对于任意单元i、j而言，将每一个物理量的上标用对应的坐标系标注，以区分不同坐标系中的物理量。对于每个单元，单元中两个节点之间满足对偶变换关系，各物理量之间的关系为

Nij=Nji,Qij=Qji,Mij=-Mji,uij=-uji,

vij=-vji,φij=φji

(2)

式(2)中：Nij、Qij、Mij分别为梁的轴向力、剪切力以及弯矩；uij、vij、φij分别为3个方向的位移分量。

将单元坐标系中的广义力与广义位移之间的关系表示为

(3)

将上述关系矩阵分别定义为广义力坐标变换矩阵，广义位移坐标变换矩阵为

(4)

3.4 行波解及其矩阵形式

现有的梁理论主要是Euler-Bernoulli梁理论和Timoshenko梁理论。其中在实际应用过程中发现，Euler-Bernoulli梁理论的结果只有当细长梁的低频情况下才和理论值相接近，当在高频区段或者梁模型为短粗梁时，其理论计算结果与实际结果相差甚远[15]。随着时代的进步以及科学情况的发展，人们提出了Timoshenko梁理论，该理论不仅仅考虑到转动惯量的影响，并且还考虑到梁的剪切变形。这个理论极大地改变了梁的动力学理论，提高了计算的精度，具有极大的工程应用价值[17]。对于梁的轴向波的控制微分方程，Timoshenko梁理论与经典的梁理论是相同的，在笛卡尔坐标系中，考虑梁的弯曲变形之中剪切变形和转动惯量的影响，其控制微分方程[5-6]为

(5)

式(5)中：E(x)、G(x)分别为材料的拉伸和剪切弹性模量系数；ρ(x)为材料的密度；A(x)为横截面面积；I(x)为横截面二次矩；Q(x,t)为梁的剪力；M(x,t)为梁的弯矩；v(x,t)为梁的挠度位移；φ(x,t)为梁的转角位移。

对式(5)进行Fourier变化，可得

(6)

则微分方程的通解可以表示为

(7)

式(7)中：ω为振动频率；a2(ω)、a3(ω)为入射波解向量；d2(ω)、d3(ω)为入射波解向量；k2、k3为弯曲波的波数；β2、β3为比例系数，表达式为

(8)

(9)

式(9)中：ξ2、ξ3、μ2、μ3为比例系数，其具体定义为

(10)

对于梁单元的状态方程，可以得出其状态向量，并且可以得到状态方程的解，将状态方程的频域解写成矩阵形式，可以得到形式为

(11)

式(11)中：AF、DF为力传播矩阵；AV、DV为位移传播矩阵；k1为纵波波数，k1=ω/c1。上述物理量的具体矩阵形式可以表示为

(12)

3.5 单元分析与相位关系

根据单元内对偶变换以及公式推导，可以得到关系式为

(13)

经过定义可以得到对应的相位关系为

(14)

式(14)中：Pij为单元i、j的相位矩阵。

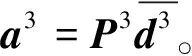
(15)

由上文所得节点相位关系，将所有节点的局部相位矩阵按照节点编号的顺序组成总体相位矩阵为

(16)

式(16)中：P为相应的总体相位关系矩阵，是6N×6N阶的对角阵。单元总体的入射波向量和出射波向量可以分别表示为

(17)

引入转换矩阵，得出整体散射矩阵为

(18)

式(18)中：U0为转换矩阵，其每一行、每一列有且只有一个元素为1，可以得到整体散射矩阵：a=PUd。

3.6 节点分析与色散关系

根据广义力平衡关系，以节点i为例，设节点i的相关单元数为ni，可以写出在频域内的平衡方程[7]为

(19)

式(19)中：M、K、u、f为相应单元的质量矩阵、刚度矩阵、位移向量以及外载荷向量。

将式(12)代入式(19)中，得

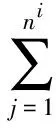
fi=(-ω2Mi+Ki)ui

(20)

Tij[Vij(0,ω)]=ui,j=1,2,…,nj

(21)

将式(21)代入式(20)中，可得

(22)

di=Siai+si

(23)

式(23)中：Si为局部散射矩阵；si为外载矩阵。

(24)

同时，按照节点顺序得出相应的散射矩阵S[8]，即

d=Sa+s

(25)

根据结构受到的周期载荷，如位移u(t)=u(ω)eiωt，作用时产生的动力响应成为稳态响应，分别定义力向量和位移向量为

(26)

进而可得

(27)

式(27)中：AFO和DFO为整体广义位移的传播矩阵；AVO和DVO为整体广义力的传播矩阵。

4 数值计算与比较

4.1 理论计算与有限元仿真

为了减小与一维声子晶体模型与实际工程应用的差别，取一维等截面声子晶体角梁的左端面为激励输入段，取角梁的最右端面为响应拾取端，并且取自由边界条件进行理论计算。于激励输入端输入振幅为1 mm的轴向位移激扰，取右端的输出位移响应，进行数据处理。

对一维等截面声子晶体角梁结构进行有限元仿真计算，需要对其进行设置，其具体参数如下：①材料参数与周期结构物理参数：与前文结构描述相同；②离散化处理：对整体模型进行自由网格划分的方法，将每一个离散化单元的尺寸定义为2 mm；③施加载荷：主要研究一维等截面声子晶体对轴向波的传输特性，因此施加轴向简谐位移载荷，位移的幅值为1 mm,激振频率范围为0～30 kHz；④分析模块设置：采用谐响应分析模块，因施加的是位移载荷，因此采用完全法进行有限元模拟仿真计算，具体如图6所示。

图6 有限元模拟仿真示意图

为了进行回传射线矩阵法计算得出的频率响应曲线与有限元分析软件计算的曲线对比，由图7中可以看出，二者重合程度较为良好，可以证明由回传射线矩阵法计算的一维等截面声子晶体角梁结构得出的频率响应函数曲线的正确性。可以看出，在0～30 kHz的频率范围内，一维等截面声子晶体角梁存在着较多的振动带隙，并且在相应的带隙范围内存在表面局域态现象，在各自的振动带隙的范围内，最大衰减程度较少，对输入激励的传播抑制程度较低。

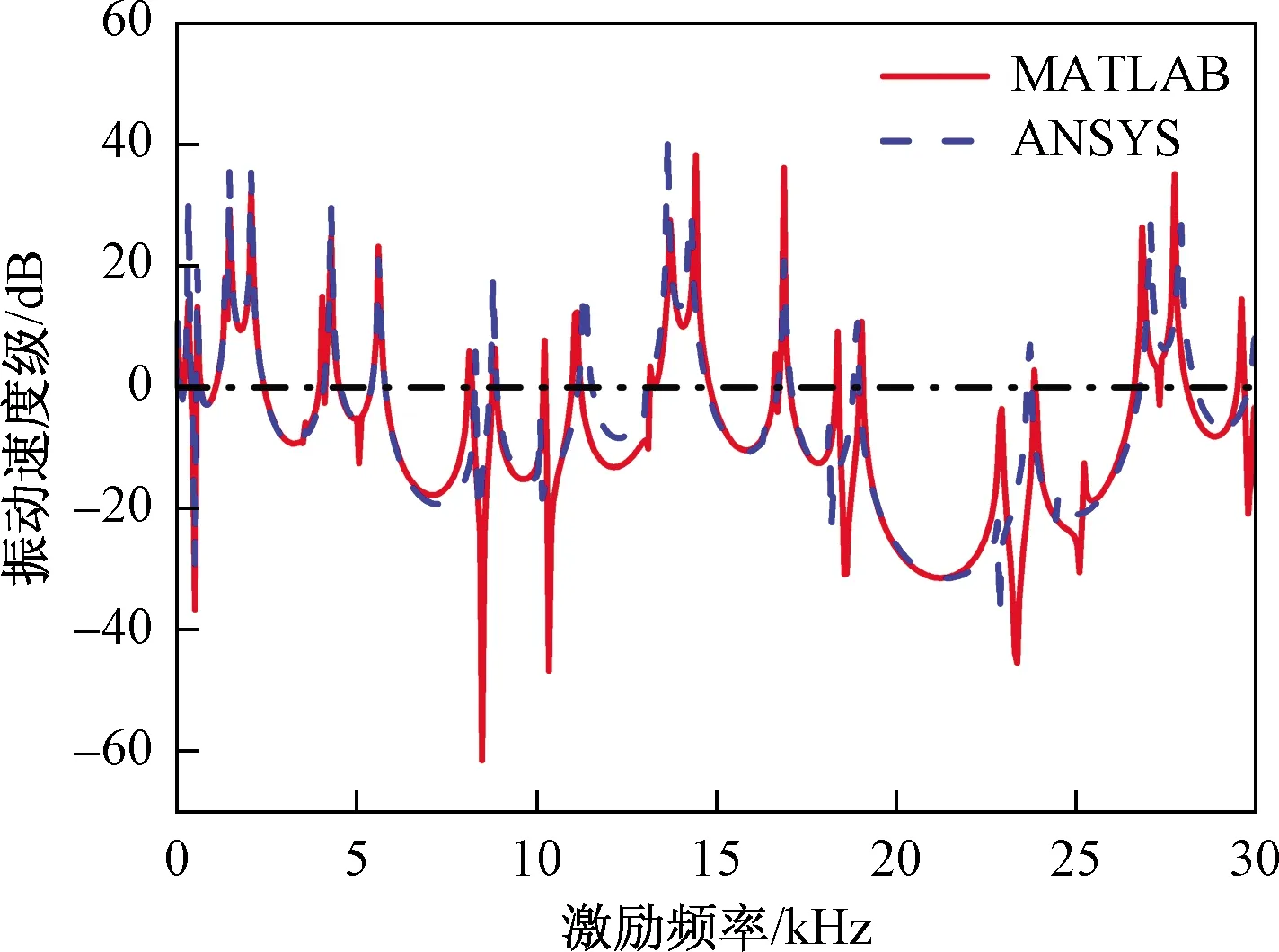
图7 有限元仿真与数值计算的对比

4.2 晶格常数N的影响

为了分析研究晶格常数N对一维有限尺寸等截面声子晶体角梁振动特性的影响，将不同晶格常数N对应的频率响应曲线进行比较分析研究。取N的范围为100～140 mm，得出各自晶格常数N对应的频率响应曲线。通过图8中各条曲线可以观察出，在0～35 kHz的频率范围内，随着晶格常数N的增加，频率响应曲线对应的振动带隙以及带隙范围内的最大衰减程度变化规律不是特别明显，但是可以比较出随着晶格常数N的增加，0～35 kHz频率范围内的带隙数量增加。

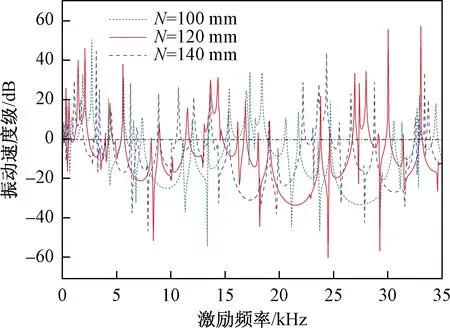
图8 不同晶格常数N对应的频响曲线

4.3 组分比g的影响

为了比较分析研究单一组成材料的长度对一维声子晶体角梁振动特性的影响，改变材料A，即材料有机玻璃的长度，将其长度定义为l1，得到不同的组分比，通过组分比的变化，得出相对应的频率响应函数曲线。在图9中可以看出，在0～35 kHz的频率范围内，随着组分比u的变化，各曲线对应表达的振动特性不是十分明显。

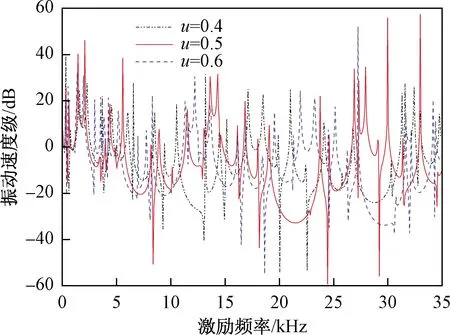
图9 不同组分比u对应的频响曲线

4.4 角梁夹角角度θ的影响

为了研究比较分析一维声子晶体角梁的夹角θ对振动特性的影响，通过改变夹角θ的大小，得到夹角θ分别为60°、90°和120°所对应的频率响应函数曲线。通过图10可以看出，随着一维等截面声子晶体角梁夹角θ的变化，各个夹角所对应的曲线基本吻合，变化的幅度不是很大。因此，角梁夹角θ对一维等截面声子晶体角梁的振动特性影响不大。

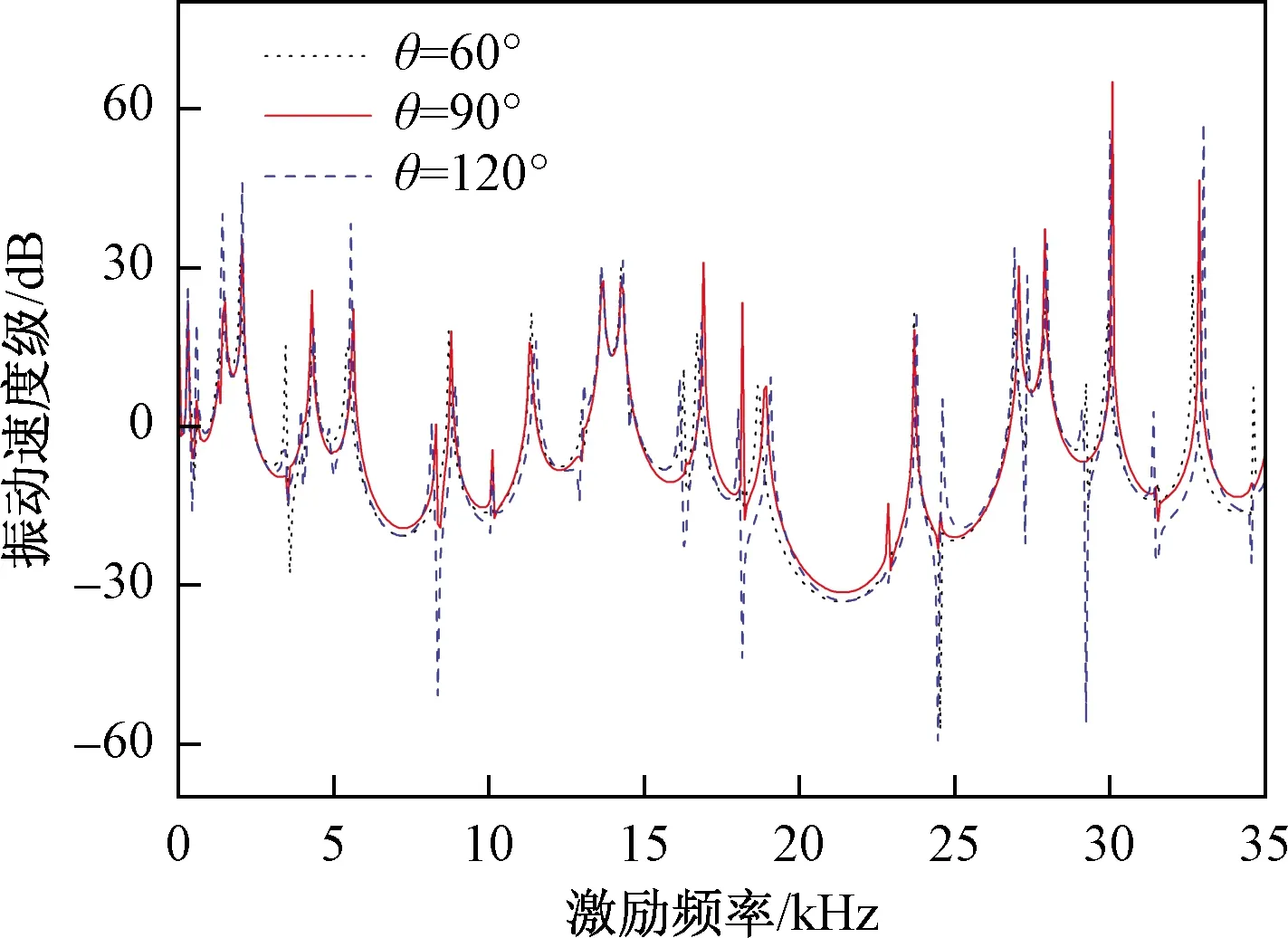
图10 不同夹角θ对应的频响曲线

4.5 横截面形状的影响

分别将横截面的形状参数设计为：圆形横截面r1=5 mm，矩形横截面b1=10 mm，h1=8 mm；正方形横截面b2=h2=10 mm。通过图11可以看出，三种横截面所对应的频率相应函数曲线中，各个横截面形状对应的频率响应函数曲线在0～35 kHz的频率范围内，其带隙宽度，带隙的起始频率，截止频率以及带隙范围内的最大衰减程度基本上保持不变，因此，横截面形状对一维等截面声子晶体角梁的振动特性的影响较小。

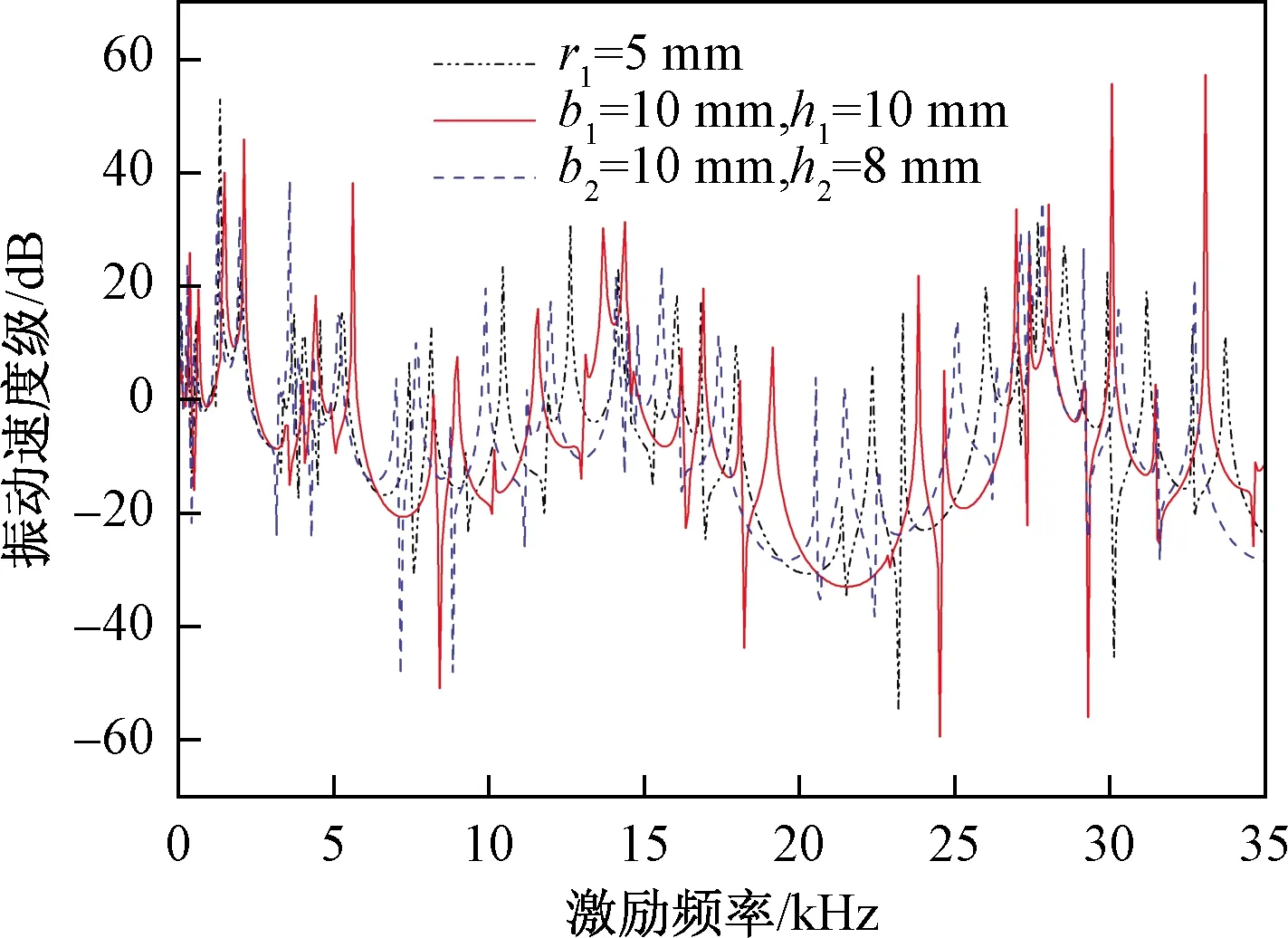
图11 不同横截面形状对应的频响曲线

5 结论

基于Timoshenko梁理论，以及回传射线矩阵法对等截面一维声子晶体角梁结构对于轴向波的振动特性进行研究，对角梁形式的一维声子晶体角梁结构的振动特性进行计算，并选取有限元分析法作为参考，证明了算法的正确性。通过相应的频率响应函数曲线之间的不同，比较分析了各参数对声子晶体角梁振动特性的影响及相应规律。