火星精确着陆轨迹优化与制导技术研究进展

龙嘉腾 葛丹桐 崔平远

火星精确着陆轨迹优化与制导技术研究进展

龙嘉腾1,2,3葛丹桐1,2,3崔平远1,2,3

（1 北京理工大学宇航学院，北京 100081）（2 深空自主导航与控制工信部重点实验室，北京 100081）（3 飞行器动力学与控制教育部重点实验室，北京 100081）

轨迹优化与制导技术是实现火星表面精确着陆的核心技术之一。文章对典型的火星着陆探测任务进行了分析，阐明了火星着陆轨迹优化与制导技术所面临的挑战。在此基础上，回顾了近年来火星着陆轨迹优化与制导技术的研究现状。最后，对未来火星着陆探测轨迹优化与制导技术的发展方向进行了展望。

火星精确着陆 轨迹优化 着陆制导 大气进入 动力下降 深空探测

0 引言

2020年7月23日，中国首个火星着陆探测器“天问一号”在海南文昌发射场成功发射，开启了为期10个月的火星之旅。“天问一号”于2021年2月10日成功进入火星环绕轨道，并于2021年5月15日成功实现火星着陆。与已有火星着陆探测任务相比，“天问一号”火星着陆探测任务的最大亮点是在首次探测任务中一次性完成“绕、落、巡”三项任务。这展现了中国深空探测任务的高目标和高起点。

从20世纪60年代开始，人类便开始了针对火星的探测活动。随着探测活动的深入和探测技术的发展，火星探测方式逐渐从飞越、环绕向着陆和采样返回发展。火星着陆和采样返回代表着当前探测的最高技术水平，具有技术风险高、资金投入高、科学回报高的特点。为此，实现火星表面精确着陆是对火星表面高科学价值区域开展探测活动的必要前提，而高精度自主导航与制导技术是实现火星表面精确着陆的重要技术基础。

与地球相比，火星大气密度极为稀薄（约为地球1/100）[1]，致使传统的地球再入过程所采用的气动减速方式难以对火星着陆器的机械能进行完全耗散。因此，目前火星着陆过程普遍采用大气进入制动、减速伞制动、动力制动相结合的方式对着陆器机械能进行耗散，并最终通过着陆腿、安全气囊[2]或空中吊车[3]的方式对着陆器进行安全施放（如图1所示）。整个火星着陆过程阶段众多，环环相扣，任何一个环节的失误都将导致整个任务的失败。因此，火星着陆探测任务风险高、技术难度大、成功率低。表1给出了火星着陆探测的典型任务。需要指出的是，表1中的火星海拔高度通常指的是火星轨道器激光高度计（Mars Orbiter Laser Altimeter，MOLA）的高度。

图1 三种火星着陆方式示意

为对火星进行更为深入的科学探测，未来火星着陆探测任务将需要探测器在火星表面高科学价值区域实现精确着陆。为此，在分析火星环境中探测器动力学行为特征的基础上，需要深入地研究火星表面精确着陆轨迹优化与制导方法。火星着陆轨迹优化技术与制导技术是两个相互联系的研究领域。轨迹优化技术是初始状态[4]和着陆点评估[5]重要工具，同时，轨迹优化技术也是制导算法中轨迹设计的重要手段。

表1 火星着陆探测典型任务分析

Tab.1 Brief summary of the typical Mars landing missions

1 火星着陆轨迹优化与制导问题

1.1 火星着陆探测任务回顾

着陆轨迹优化与制导是实现火星表面精确着陆的重要技术基础和发展趋势。2011年，在美国“好奇号”探测任务中首次采用大气制导，使着陆精度显著提高。“毅力号”探测任务继承了“好奇号”中的技术经验，图2给出了“毅力号”探测器着陆过程（图2中E是指进入点时刻）。与“好奇号”探测器着陆过程相似，“毅力号”探测器着陆过程主要分为大气进入段、伞降段、动力下降段和最终着陆段。其中大气进入段和动力下降段采用受控飞行方式，其制导与控制精度将决定最终着陆精度。火星大气进入段与地球大气再入过程相似，通过设计合理的飞行气动外形，采用大气阻力（摩擦阻力、激波阻力等）对飞行器初始机械能进行耗散。相比于地球大气再入过程，由于火星大气密度十分稀薄，在火星大气进入段，飞行器通常将飞行高度降至足够低才能产生显著的大气阻力作用。这导致在大气进入段末端，飞行器的飞行高度通常很低，从而显著降低了最终着陆海拔高度，进而使火星表面的可选着陆区范围由于海拔高度的因素而严重受限。

图2 “毅力号”探测器进入、下降与着陆过程

火星动力下降段通常采用反推控制系统进行位置和姿态控制。这种控制方式从本质上讲与月球软着陆是相同的。不同之处在于火星相比于月球更加遥远，对地通信存在显著延迟，通过地面进行实时控制难度大。因此，在火星动力段中，需要制导与控制系统具备较强的自主能力，尤其是实时表面形貌障碍检测与规避能力，对着陆安全具有重要影响。

1.2 火星着陆轨迹优化与制导所面临的挑战

（1）火星大气进入动力学呈现强非线性和不确定性

火星大气进入过程是通过控制飞行器所受的气动力来完成轨迹控制和减速制动的。因此，在大气进入动力学中存在大量与气动力相关的非线性关系，包括密度−高度关系、气动力−密度关系、气动力−马赫数−攻角关系等[6]，这些非线性关系导致整个进入动力学过程异常复杂，各状态量间的数量级差异巨大，使轨迹优化和制导指令解算过程中收敛域狭窄，易陷入局部极值。图3给出了火星大气密度偏差随海拔高度的变化关系。从图3中可以看出，火星大气密度不确定性随着海拔高度的增大而显著增强，进而导致飞行器进入动力学模型存在显著的不确定性。

图3 火星大气密度偏差随高度的分布情况

出于科学探测需要，未来火星探测任务将倾向于采用更大着陆质量的探测器。从表1可以清楚看出这种趋势，相较于以往探测任务，“好奇号”和“毅力号”探测器的质量提高了一个数量级。重载条件下对着陆轨迹优化与制导技术带来的挑战是多方面的。在重载条件下，为实现安全着陆，飞行器必须具备更高的减速效率，而与此同时，这将导致热流峰值和过载峰值的显著升高。如何在减速制动效率和飞行安全之间取得平衡，既是飞行器结构和热防护设计所需面对的问题，也是着陆轨迹优化与制导所需解决的关键技术。同时，目前条件下的飞行器进入段末端高度普遍较低，进而从着陆高度上显著限制了飞行器可探测的区域，而大质量飞行器也将使这一问题更加突出。

（2）火星大气进入过程控制能力严重受限

图4 “好奇号”弹道升力式进入飞行器受力分析图

由于火星大气密度十分稀薄，在大气进入段开始后相当长的一段时间内，由于大气密度低导致飞行器动压不足，进而受到升力也极其有限，显著抑制的大气进入过程前半段的轨迹控制能力。而随着动压的逐步建立，飞行器又很快经历热流峰值和过载峰值等路径约束。这些保证飞行安全的路径约束又要求飞行器动压不能过大，也在一定程度上限制了飞行器的机动能力。同时，由于倾侧角调节要同时兼顾纵向运动和侧向机动能力，导致飞行器控制能力严重受限。

（3）火星着陆过程约束类型复杂

火星着陆存在大气制动、减速伞制动、动力制动等多种制动方式[7]，飞行过程环境复杂，所涉及的飞行器类型众多。不同的制动方式、环境特征和飞行器特性导致着陆轨迹优化与制导算法设计中遇到大量复杂的约束类型。

在火星着陆轨迹优化与制导算法设计过程中，除需要满足动力学约束和两点边值约束外，根据大气进入段和动力下降段的不同特点，还需分别满足相应的约束以保证飞行安全。在大气进入段中，飞行器的初始机械能通过摩擦阻力、激波阻力的方式转化为内能加以耗散。因此，在大气进入过程会产生大量的热能，极大威胁飞行器的安全。此外，飞行器受到的气动过载也是威胁结构安全的重要因素。因此，大气进入段保障飞行安全的路径约束主要有峰值热流约束和峰值过载约束。由于火星着陆探测区域通常选择在大型陨石坑等具有高科学价值的区域，在动力下降段中飞行器将面临火星表面复杂形貌带来的威胁。图5给出了火星“好奇号”探测器和“毅力号”探测器任务着陆区。从图中可以看出，火星表面着陆区形貌十分复杂。因此，复杂形貌下的障碍规避约束是保障着陆过程飞行安全的重要约束条件。如何针对火星表面复杂的形貌特征开展避障轨迹和制导算法[8]设计，是火星动力下降段轨迹优化与制导技术所需解决的关键问题。

图5 火星着陆任务目标着陆区

2 火星着陆轨迹优化与制导研究现状

火星着陆环境建模是实施火星表面精确着陆的前提，火星大气模型是影响火星着陆精度的重要环境模型；另一方面，火星着陆轨迹边界条件选择是影响着陆轨迹特性的重要因素，可控集、可达集是进行边界条件选择的重要工具。本节首先对火星大气建模以及着陆轨迹边界条件的可控集/可达集设计方法的研究现状进行归纳。在此基础上，对火星着陆轨迹优化与制导方法研究现状展开分析。

（1）火星大气的精确建模研究现状

由于火星大气是进入段所依赖的主要减速介质[9]，其精确建模也是实现精确制导和控制的必要前提。火星大气存在显著的不确定性，这种不确定性与季节、海拔高度等因素存在密切关系，且存在局部阵风等不确定因素。

影响大气进入段动力学建模的主要火星大气参数是大气密度和大气温度。目前，针对火星大气建模较为精确的是美国火星全球参考大气模型（Mars Global Reference Atmospheric Model，Mars-GRAM）和欧洲的火星气候数据库（Mars Climate Database，MCD）。两个数据库均较为详细完整地给出了火星各主要参数，但由于数据量庞杂，不便于大气进入轨迹优化和制导算法设计。虽然火星大气密度随高度的分布呈现非严格指数形式，但在一定高度范围内具有显著的指数形式特征。文献[9]给出了火星大气三维解析模型，对火星大气密度模型进行了分层简化。因此，在大气进入制导律设计、分析与验证过程中选取密度模型来计算气动力、气动过载和气动加热效应[10]时，需要在精确性与复杂性之间取得平衡。由于单层大气密度指数模型形式简单且具有良好的解析性质，在火星大气进入制导方法的理论研究中应用最为广泛。由于火星大气密度模型形式多样，其繁简程度、精确程度存在显著差异。而在算法验证阶段，则需要采用更为精确的模型进行试验验证。

（2）火星着陆可控集、可达集分析研究现状

在复杂约束条件下，火星着陆可控集[4]与可达集[11]设计与分析是基于轨迹优化技术的重要应用方向。着陆可控集与可达集的概念来源于现代控制理论。在火星着陆过程中，可控集为标称末端状态对应的所有可能初始状态的集合；可达集为标称末端状态下的所有可能末端状态的集合。着陆可控集与可达集是进行着陆初始状态（大气进入状态）与着陆末端状态（着陆点）设计的重要依据，也是分析着陆轨迹特性的重要手段。

从形式上看，可控集与可达集的解算过程是互逆的。但求解过程中，由于可达集计算中，着陆轨迹的初始状态约束可以直接通过动力学积分满足；而可控集计算中，着陆轨迹末端约束的满足则需要通过复杂的迭代运算。因此，可控集的求解难度和复杂度显著高于可达集。由于大气进入过程中的气动阻力以及动力下降段的反推控制力等非保守力的存在，所以在两个阶段中均无法通过动力学反演来实现可控集的快速解算。着陆可控集与可达集的计算通常采用轨迹优化方法。由于大气进入段和动力下降段动力学和约束条件的非线性特征，连接给定初始状态和末端状态的着陆轨迹通常不止一条，为分析可控集、可达集内的初始状态或末端状态特性，采用轨迹优化方法获取相应性能指标下的着陆轨迹以及相应的可控集、可达集是通常做法。文献[4]针对大气进入段进入点设计的角度出发，研究了进入飞行器气动参数与大气密度对可行初始状态集合（即能控集合）的影响，并提出了动变参数在不同扰动水平下的能控交集（如图6所示），为扰动条件下进入条件的鲁棒选取提供了依据。文献[12]对火星动力段中的轨迹优化问题进行了凸化处理，在此基础上采用凸优化技术解算火星动力下降段能控集与能达集。

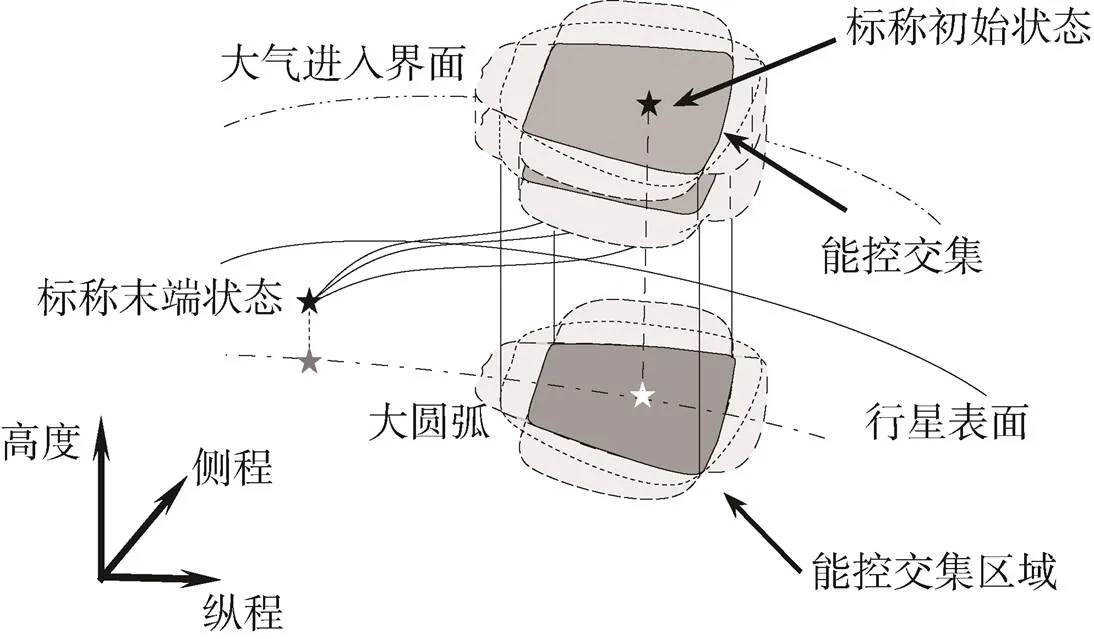
图6 行星着陆能控交集示意

（3）火星着陆轨迹优化技术研究现状

火星着陆轨迹优化问题是通过特定优化方法，寻找满足相关约束的、使性能指标最优的控制指令及飞行轨迹（飞行状态）。为保证飞行安全与着陆精度，火星着陆过程需要满足多种工程约束。

传统轨迹优化方法主要分为直接法和间接法。直接法通过设计离散节点，并在节点处离散控制变量，或对控制变量和状态变量同时离散。将离散后的变量作为优化变量，采用非线性规划方法，在相应的动力学约束、边界约束、路径约束、控制约束下获得最优轨迹。该方法物理概念明确，但由于大量约束条件的存在使可行域变窄，同时非线性动力学又很容易使优化过程陷入局部极小。与此相对，间接法是从极小值原理出发，求解出最优轨迹所需满足的一阶必要性条件，进而获得最优轨迹。该方法从理论上保证了所获得轨迹的最优性，但这也同时大大限制了解算收敛域，导致整个解算过程对协态变量的初值猜测极为敏感，加之协态变量没有明确的物理概念，因此该方法在应用上受到很大局限。

近年来，凸优化方法由于在求解精度和计算效率方面的明显优势，受到了国内外学者的广泛关注。尤其是内点法在求解凸优化问题时能够在多项式时间内，以给定精度完成问题的求解[13]。凸优化在大气进入段和动力下降段的轨迹优化中均得到了有效的应用。大气进入动力学呈现强非线性，且非凸特征显著，加之多种非凸约束的存在，难以直接采用凸优化方法进行求解。针对火星大气进入过程中的动力学非线性和控制非线性问题，文献[14]采用局部线性化和变量松弛技术分别将强非线性的大气进入动力学进行等效凸化，并采用二阶锥规划方法实现了对大气进入最优轨迹的有效求解，而上述方法在一定程度上对求解非线性规划的凸化方法具有普适意义。针对气动力与状态间的强非线性耦合关系，文献[15]采用序列凸优化技术，有效解决了约束条件下的最优进入轨迹的凸优化解算。动力下降段中由于动力学形式相比于大气进入段较为简单，其轨迹优化问题主要集中于约束处理。针对动力下降段中的推力幅值非凸约束，文献[16-17]采用松弛变量技术，将环状非凸幅值约束转化为凸台状凸约束进行求解。

（4）火星大气进入制导方法研究现状

未来火星探测对着陆精确性提出了更高要求。自“好奇号”探测器首次采用大气进入制导技术以来，火星着陆精度有了显著提升。火星环境的不确定性和多源扰动是影响火星表面精确着陆的重要因素，这一问题在大气进入段尤为突出。因此，在分析多源扰动和不确定性对着陆精度不利影响的基础上，设计相应的精确制导方法，是大气进入段制导设计的关键内容。

大气进入段动力学呈现强非线性，无法获得制导指令的解析形式。针对这一特点，大气进入制导方法[16]通常可分为标称轨迹法[18-20]和预测制导法[21-22]。标称轨迹法是采用离线或在线轨迹设计方法，获得标称条件下的进入轨迹，并通过相应轨迹跟踪律[23-25]对标称轨迹进行实时在线跟踪，进而满足路径约束和末端着陆精度。而预测制导法借鉴了模型预测控制的思想，在每个制导周期开始时，采用在线动力学模型将当前状态数值递推至末端条件处，以末端偏差作为反馈对当前标称制导指令进行修正，从而满足末端着陆精度要求。文献[26]以末端高度为性能指标，提出了大气进入最优制导律，通过在线计算切换时刻，可以实现良好的末端精度并使末端高度最优，该方法从本质上讲是一种预测制导方法。文献[21,27]结合小升阻比飞行器，解决了预测制导方法中的路径约束问题。文献[23]针对标称轨迹法在跟踪过程中存在的控制饱和问题，提出了基于障碍李雅普诺夫函数的滑模跟踪控制方法。针对进入段大气环境的不确定性，文献[28]基于线性协方差理论计算大气进入过程中的不确定传播规律，以提高末端高度的同时，减小末端高度的散布为性能指标，获得了不确定条件下的末端高度最优进入轨迹。

近年来的研究显示，以“好奇号”探测器为代表的着陆技术在提高着陆海拔与着陆精度方面，已经逐渐遇到了瓶颈。因此，对传统“好奇号”探测器着陆方式的变革已经势在必行。为此，在大气进入段中采用更高升阻比的飞行器以提高机动能力和减速效率是重要的发展方向，国内外学者也对未来火星着陆的模式进行了大量的创新工作[29-31]。图7给出了两类典型的火星着陆新概念飞行器。相比于传统火星大气进入飞行器，高超声速可充气式进入飞行器通过在火星大气进入过程中充气热盾，能够形成直径更大的进入飞行器，使大气进入过程中飞行器所受到的热流更低、形成的气动阻力更大，进而获得更加良好的减速特性，因而在载人火星探测等重载条件下的火星着陆任务中有良好的应用前景。中升阻比火星进入-着陆器则是在火星大气进入段和动力下降段采用统一飞行器外形，将较于传统探测方式，所执行的操作更少，可靠性更高；同时相较于传统小升阻比进入飞行器，中升阻比飞行器可以在大气进入段产生更大的升力，进而可以获得更为良好的机动能力并提高着陆载荷的运载能力。

（5）火星动力下降段制导方法研究现状

在动力下降段中，由于火星表面的高科学价值目标往往位于陨石坑边缘等形貌复杂区域，这些区域特征复杂且存在大量未知地形，因此如何在复杂形貌下进行有效的障碍规避，是动力下降段制导律设计的核心内容之一。火星动力下降段的制导方法，最初来源于阿波罗登月过程中的月球软着陆制导。在此基础上衍生出了燃耗最优制导[32-33]、凸规划制导[16]、ZEM/ZEV制导[34]、凸曲率制导[35]、基于模型预测控制的着陆制导[36]等。针对火星动力下降段中存在的大量危险地形，文献[35]提出了一种凸曲率制导思想，该方法通过寻求几何凸曲率轨迹的存在条件，设计相应的曲率制导算法，可以实现对潜在障碍的有效规避，并能够显著提高光学导航系统对目标着陆区的可见性。图8给出了几何凸轨迹在障碍规避及相机视场方向的优势。针对火星动力下降段复杂约束条件下的轨迹优化问题，“矢量轨迹”方法[37]通过轨迹的矢量描述、约束的矢量表达、规划的矢量求解，将非凸几何约束着陆轨迹优化问题，转化为二阶锥规划问题实现快速求解。

图7 火星着陆新概念飞行器

图8 几何凸轨迹在障碍规避及相机视场方向的优势[28]

3 火星着陆轨迹优化与制导关键技术

（1）复杂着陆环境的精确建模技术

火星着陆环境异常复杂，其中火星大气和表面形貌是影响火星表面精确着陆的重要因素。火星大气作为进入段的重要减速介质，其强不确定性对动力学建模和精确制导带来巨大影响。另一方面，在动力下降段中，火星表面复杂形貌是制约飞行安全的重要环节。因此，对火星着陆环境的精确建模是实现火星表面精确着陆的重要前提。

（2）非一致约束条件下的着陆轨迹优化技术

为保证着陆精度和飞行安全，火星着陆轨迹优化中需考虑大量复杂约束，如动力学约束、边界条件约束、路径约束等。这些约束导致轨迹优化问题的可行解空间狭窄，对优化算法的解算效率和求解精度带来巨大挑战，极易出现求解发散和陷入局部最优的情形。目前，虽然凸优化方法为着陆轨迹优化技术的发展带来了新契机，但其对约束形式的严苛要求严重制约了其应用范围。因此，非一致约束的处理是火星着陆轨迹优化问题的关键。

（3）不确定条件下的着陆精确制导技术

火星着陆过程中存在大量的不确定因素。在极端条件下，这些不确定因素将导致制导算法发散，严重影响飞行安全及着陆精度。为实现精确着陆，相应的制导算法需具备对不确定因素的自适应性或鲁棒性。为应对不确定因素导致的制导算法不收敛的情况，未来着陆精确制导技术需具备着陆轨迹的在线重规划能力，为极端不利条件下更新着陆轨迹提供依据。

4 结束语

轨迹优化与制导是火星表面精确着陆的关键技术。本文首先对火星着陆探测的典型任务进行了回顾，并结合火星着陆过程中的特殊环境分析了着陆轨迹优化与制导所面临的挑战。梳理了火星着陆轨迹优化与制导技术的研究现状，并对未来发展趋势进行了总结。

目前，国内外已对火星着陆轨迹优化与制导技术开展了大量研究和验证工作，并针对未来火星着陆技术的发展趋势，提出了大量轨迹优化与制导技术的新理论、新方法。“毅力号”火星着陆与采样返回任务继承了大量“好奇号”探测任务的着陆技术。这表明在现有技术水平下，以“好奇号”为代表的火星着陆技术已经日渐成熟。随着火星着陆技术的不断发展，未来火星着陆将向着更大着陆质量、更高着陆海拔、更高着陆精度的方向发展。这势必带动火星着陆技术变革，也为中国在未来的火星探测中实现弯道超车，占领火星探测乃至深空探测的技术制高点提供了历史性的新契机。

[1] BRAUN R D, MANNING R M. Mars Exploration Entry, Descent, and Landing Challenges[J]. Journal of Spacecraft and Rockets, 2007, 44(2): 310-323.

[2] MCGRATH D, KIRSCHNER T, MIONSKE G, et al. Mars Pathfinder Airbag Gas Generator Development[C]//34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, July 13-15, 1998, Cleveland, Ohio, USA.

[3] ANTOUN G, NAYERI R, PENG C Y, et al. Refinements to the MSC/Adams Model of the Skycrane Event for the Mars 2020 Rover[C]//AIAA Scitech 2020 Forum, January 6-10, 2020, Orlando, Florida, USA.

[4] LONG J T, GAO A, CUI P Y. Controllable Set Analysis for Planetary Landing Under Model Uncertainties[J]. Advances in Space Research, 2015, 56(2): 281-292.

[5] 葛丹桐, 崔平远. 地外天体着陆点选择综述与展望[J]. 深空探测学报, 2016, 3(3): 197-203.

GE Dantong, CUI Pingyuan. Overview and Prospect of Planetary Landing Site Selectio[J]. Journal of Deep Space Exploration, 2016, 3(3): 197-203. (in Chinese)

[6] 梁杰, 李志辉, 杜波强, 等. 真实气体效应对MSL火星进入气动特性的影响研究[J]. 航天返回与遥感, 2017, 38(4): 8-17.

LIANG Jie, LI Zhihui, DU Boqiang, et al. Numerical Research of Real Gas Effect on MSL Mars Entry Aerodynamic Characteristics[J]. Spacecraft Recovery & Remote Sensing, 2017, 38(4): 8-17. (in Chinese)

[7] 张青斌, 丰志伟, 马洋, 等. 火星EDL过程动力学建模与仿真[J]. 宇航学报, 2017, 38(5): 443-450.

ZHANG Qingbin, FENG Zhiwei, MA Yang, et al. Modeling and Simulation of Mars EDL Process[J]. Journal of Astronautics, 2017, 38(5): 443-450. (in Chinese)

[8] 崔平远, 高艾, 朱圣英. 深空探测器自主导航与制导[M]. 北京: 中国宇航出版社, 2016: 4-6.

CUI Pingyuan, GAO Ai, ZHU Shengying. Autonomous Navigation and Guidance for Deep Space Exploration[M]. Beijing: China Astronautic Publishing House, 2016: 4-6. (in Chinese)

[9] 秦同, 王硕, 高艾, 等. 一种火星大气密度三维解析模型[J]. 深空探测学报, 2014, 1(2): 117-122.

QIN Tong, WANG Shuo, GAO Ai, et al. Three-dimensional Analytical Model for Mars Atmospheric Density[J]. Journal of Deep Space Exploration, 2014, 1(2): 117-122. (in Chinese)

[10] 唐伟, 杨肖峰, 桂业伟, 等. 火星进入器高超声速气动力/热研究综述[J]. 宇航学报, 2017, 38(3): 230-239.

TANG Wei, YANG Xiaofeng, GUI Yewei, et al. Review of Hypersonic Aerodynamics and Aerothermodynamics for Mars Entries[J]. Journal of Astronautics, 2017, 38(3): 230-239. (in Chinese)

[11] 赵泽端, 崔平远, 朱圣英. 火星大气进入段纵向可达区生成的解析同伦法[J]. 宇航学报, 2019, 40(9): 1024-1033.

ZHAO Zeduan, CUI Pingyuan, ZHU Shengying. An Analytical Homotopic Method to Generate the Reachable Longitudinal Area for Mars Entry[J]. Journal of Astronautics, 2019, 40(9): 1024-1033. (in Chinese)

[12] EREN U, DUERI D, AÇIKMEŞE B. Constrained Reachability and Controllability Sets for Planetary Precision Landing via Convex Optimization[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(11): 2067-2083.

[13] BOYD S, VANDENBERGHE L. Convex Optimization[M]. New York: Cambridge University Press, 2004: 7-8.

[14] LIU X F, SHEN Z J, LU P. Entry Trajectory Optimization by Second-order Cone Programming[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(2): 227-241.

[15] WANG Z B, GRANT M J. Constrained Trajectory Optimization for Planetary Entry via Sequential Convex Programming[J]. Journal of Guidance, Control, and Dynamics, 2017, 40(10): 2603-2615.

[16] AÇIKMEŞE B, PLOEN S R. Convex Programming Approach to Powered Descent Guidance for Mars Landing[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(5): 1353-1366.

[17] AÇIKMEŞE B, CARSON J M, BLACKMORE L. Lossless Convexification of Nonconvex Control Bound and Pointing Constraints of the Soft Landing Optimal Control Problem[J]. IEEE Transactions on Control Systems Technology, 2013, 21(6): 2104-2113.

[18] 滕锐, 焦子涵, 张宇飞, 等. 火星六自由度大气进入制导方法对比分析[J]. 航天返回与遥感, 2020, 41(1): 18-27.

TENG Rui, JIAO Zihan, ZHANG Yufei, et al. Analysis and Comparison of Mars Atmospheric Entry Guidance Methods in 6-DOF Model[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(1): 18-27. (in Chinese)

[19] 龙也, 刘一武. 采用弱攻角补偿与脱敏设计的火星进入段制导[J]. 宇航学报, 2016, 37(3): 282-290.

LONG Ye, LIU Yiwu. Mars Entry Guidance with Weak Attack Angle Compensation and Desensitization Design[J]. Journal of Astronautics, 2016, 37(3): 282-290. (in Chinese)

[20] 郭敏文, 李茂登, 黄翔宇, 等. 非一致终端约束下火星大气进入段制导律设计[J]. 深空探测学报, 2017, 4(2): 184-189.

GUO Minwen, LI Maodeng, HUANG Xiangyu, et al. On Guidance Algorithm for Martian Atmospheric Entry in Nonconforming Terminal Constraints[J]. Journal of Deep Space Exploration, 2017, 4(2): 184-189. (in Chinese)

[21] ZHENG Y Y, CUI H T, AI Y H. Constrained Numerical Predictor-corrector Guidance for Mars Precision Landing[J]. Journal of Guidance, Control, and Dynamics, 2016, 40(1): 179-187.

[22] 龙嘉腾, 高艾, 崔平远. 火星大气进入段侧向预测校正制导律设计[J]. 深空探测学报, 2016, 3(2): 145-149.

LONG Jiateng, GAO Ai, CUI Pingyuan. Lateral Predictive Guidance for Mars Atmospheric Entry[J]. Journal of Deep Space Exploration, 2016, 3(2): 145-149. (in Chinese)

[23] LONG J T, ZHU S Y, CUI P Y, et al. Barrier Lyapunov Function Based Sliding Mode Control for Mars Atmospheric Entry Trajectory Tracking with Input Saturation Constraint[J]. Aerospace Science and Technology, 2020, 106(2): 106213.

[24] DAI J, GAO A, XIA Y Q. Mars Atmospheric Entry Guidance for Reference Trajectory Tracking Based on Robust Nonlinear Compound Controller[J]. Acta Astronautica, 2017, 132: 221-229.

[25] YAN H, HE Y Z. Drag-tracking Guidance for Entry Vehicles without Drag Rate Measurement[J]. Aerospace Science and Technology, 2015, 43: 372-380.

[26] LONG J T, GAO A, CUI P Y, et al. Mars Atmospheric Entry Guidance for Optimal Terminal Altitude[J]. Acta Astronautica, 2019, 155: 274-286.

[27] LU P. Entry Guidance: A Unified Method[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(3): 713-728.

[28] CUI P Y, ZHAO Z D, YU Z S, et al. Terminal Altitude Maximization for Mars Entry Considering Uncertainties[J]. Acta Astronautica, 2018, 145: 446-455.

[29] FRIZ P D. Parametric Cost Estimates of Four 20 Ton Payload Mars EDL Vehicle Concepts[C]//AIAA Scitech 2020 Forum, January 6-10, 2020, Orlando, Florida, USA.

[30] SOSTARIC R R, CERIMELE C J, ROBERTSON E A, et al. A Rigid Mid Lift-to-drag Ratio Approach to Human Mars Entry, Descent, and Landing[C]//AIAA Guidance, Navigation, and Control Conference, Janurary 9-13, 2017, Grapevine, Texas, USA.

[31] JIANG X Q, LI S, FURFARO R. Integrated Guidance for Mars Entry and Powered Descent Using Reinforcement Learning and Pseudospectral Method[J]. Acta Astronautica, 2019, 163: 114-129.

[32] 任高峰, 高艾, 崔平远, 等. 一种燃料最省的火星精确着陆动力下降段快速轨迹优化方法[J]. 宇航学报, 2014, 35(12): 1350-1358.

REN Gaofeng, GAO Ai, CUI Pingyuan, et al. A Rapid Power Descent Phase Trajectory Optimization Method with Minimum Fuel Consumption for Mars Pinpoint Landing[J]. Journal of Astronautics, 2014, 35(12): 1350-1358. (in Chinese)

[33] 郭延宁, 马广富, 曾添一, 等. 基于燃料最优解的火星精确着陆制导策略研究[J]. 深空探测学报, 2015, 2(1): 61-68.

GUO Yanning, MA Guangfu, ZENG Tianyi, et al. Mars Precision Landing Guidance Strategy Based on Fuel Optimal Solution[J]. Journal of Deep Space Exploration, 2015, 2(1): 61-68. (in Chinese)

[34] WANG P, GUO Y N, MA G F, et al. Two-phase Zero-effort-miss/Zero-effort-velocity Guidance for Mars Landing[J]. Journal of Guidance, Control, and Dynamics, 2020, 44(1): 75-87.

[35] CUI P Y, QIN T, ZHU S Y, et al. Trajectory Curvature Guidance for Mars Landings in Hazardous Terrains[J]. Automatica, 2018, 93: 161-171.

[36] GE D T, CUI P Y. Extended State Observer-based Model Predictive Control in Mars Powered Descent[C]//2018 AIAA Guidance, Navigation, and Control Conference, January 8-12, 2018, Kissimmee, Florida, USA.

[37] 崔平远, 龙嘉腾, 朱圣英, 等. 基于矢量轨迹的火星动力下降轨迹规划方法: 201910845476.8[P]. 2019-09-09.

CUI Pingyuan, LONG Jiateng, ZHU Shengying, et al. Vector Trajectory Based Mars Powered Descent Landing Trajectory Planning Method: 201910845476.8[P]. 2019-09-09. (in Chinese)

Overview of Mars Pinpoint Landing Trajectory Optimization and Guidance Techniques Research

LONG Jiateng1,2,3GE Dantong1,2,3CUI Pingyuan1,2,3

（1 School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China）（2 Key Laboratory of Autonomous Navigation and Control for Deep Space Exploration, Ministry of Industry and Information Technology, Beijing 100081, China）（3 Key Laboratory of Dynamics and Control of Flight Vehicle, Ministry of Education, Beijing 100081, China）

Landing trajectory optimization and guidance are the key techniques for Mars pinpoint landing. The typical missions of Mars landing exploration are analyzed, and the challenges of trajectory optimization and guidance techniques for Mars landing are illustrated. Then, the research progress of the Mars landing trajectory optimization and guidance are reviewed. Finally, the development trends of the landing trajectory optimization and guidance for future Mars pinpoint missions are previewed.

Mars pinpoint landing; trajectory optimization; landing guidance; atmospheric entry; powered descent landing; deep space exploration

V412.4

A

1009-8518(2021)03-0013-10

10.3969/j.issn.1009-8518.2021.03.002

2021-03-18

国家重点研发计划（2019YFA0706500）；国家自然科学基金（61873302，61973032）；基础科研项目（JCKY2018602B002，JCKY2019602D022）；民用航天预研项目；中国博士后科学基金（2020M670167，2020M680388）

龙嘉腾, 葛丹桐, 崔平远. 火星精确着陆轨迹优化与制导技术研究进展[J]. 航天返回与遥感, 2021, 42(3): 13-22. LONG Jiateng, GE Dantong, CUI Pingyuan. Overview of Mars Pinpoint Landing Trajectory Optimization and Guidance Techniques Research[J]. Spacecraft Recovery & Remote Sensing, 2021, 42(3): 13-22. (in Chinese)

龙嘉腾，男，1991年生，2020年获北京理工大学航空宇航科学与技术专业博士学位，博士后。主要研究方向为飞行器制导与控制、深空轨迹优化。E-mail：jiatenglong123@126.com。

崔平远，男，1961年生，1990年获哈尔滨工业大学一般力学专业博士学位，教授，博士生导师。主要研究方向为飞行器自主导航与控制、深空探测技术轨道设计。E-mail：cuipy@bit.edu.cn。

（编辑：庞冰）